Тема 4 Геометрическая коррекция изображений Прямая и

Тема 4. Геометрическая коррекция изображений • Прямая и обратная функция преобразования координат. • Способы задания функций преобразования координат. • Двумерная интерполяция.

• Точечные операции – изменение уровней яркости отдельных пикселей • Геометрические операции – изменение только положения пикселя

• Прямое и обратное линейное преобразование или M – отображающая ф-я x – вектор координат пикселя (x, y) старого изображения x – вектор координат пикселя (x’, y’) нового изображения прямое обратное

Однородные координаты связаны с обычными координатами соотношением: Система однородных координат позволяет: • Использовать унифицированный подход для выражения преобразований точек • Использовать матричную запись для задания перспективного преобразования • Описывать бесконечно удаленные точки • Провести различия между точками и векторами

• Аффинные преобразования, точечные взаимно однозначные отображения плоскости (пространства) на себя, при которых прямые переходят в прямые. Если на плоскости задана декартова система координат, то любое Аффинные преобразования этой плоскости может быть определено посредством т. н. невырожденного линейного преобразования координат х и у точек этой плоскости.

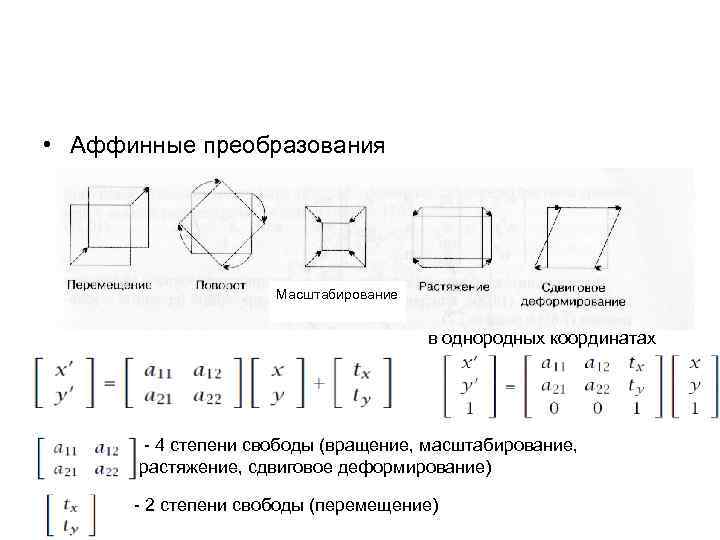
• Аффинные преобразования Масштабирование в однородных координатах - 4 степени свободы (вращение, масштабирование, растяжение, сдвиговое деформирование) - 2 степени свободы (перемещение)

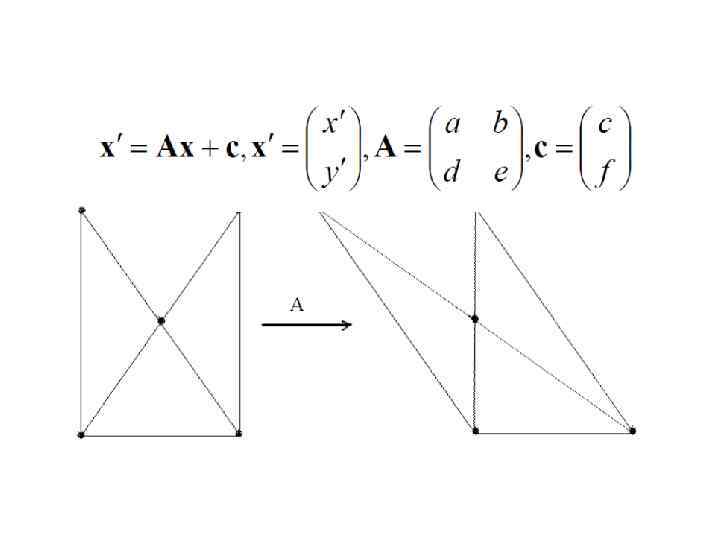
• в однородных координатах причем

частные случаи • растяжение вдоль координатных осей матрица растяжения в однородных координатах

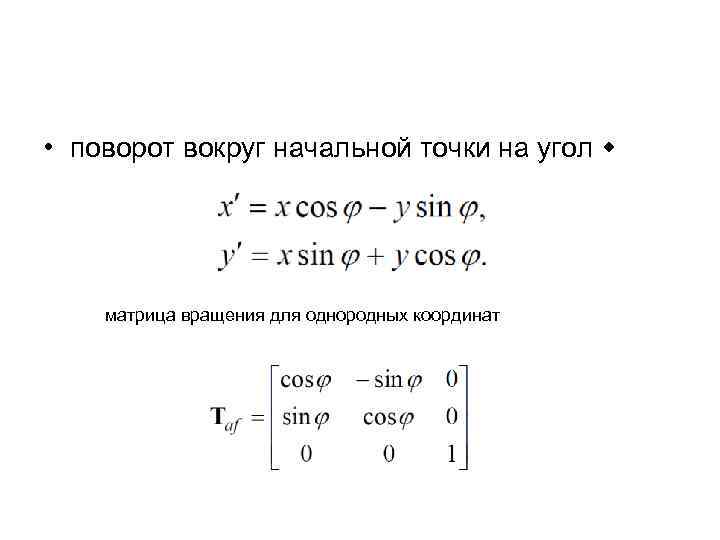
• поворот вокруг начальной точки на угол матрица вращения для однородных координат

• перенос матрица переноса

• отражение относительно какой-либо из осей (например, оси абсцисс) матрица отражения

• любое афинное преобразование может быть представлено в виде композиции последовательных приведенных выше преобразований • Обратное преобразование

• Перспективное преобразование (частный случай проективного преобразования) или дополнительные коэффициенты a 31 и a 32 описывают проективную проекцию Перспективное преобразование нелинейно!

• Области применения проективной геометрии: – – – калибровка регистрирующей камеры анализ движения по серии изображений распознавание образов реконструкция сцен по стереоснимкам синтез изображений анализ и восстановление формы

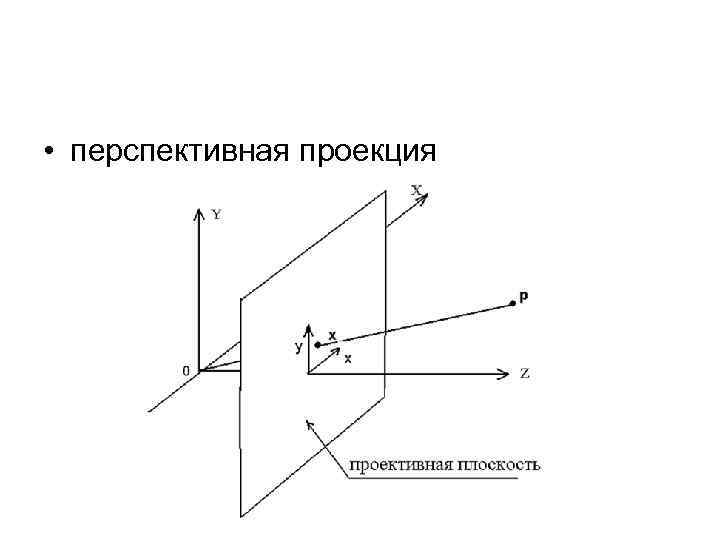
• перспективная проекция

• Интерполяция – линейная – полиномиальная – оптимизированная • с помощью сплайн-функций • метод наименьших квадратов

• интерполированное непрерывное изображение где g(t, s)- интерполирующая функция (называемая также интерполяционным ядром), h- шаг дискретизации исходного изображения, v(ih, jh) - известные отсчеты яркости в точках дискретного растра оптимальная интерполяция – sinc(x)

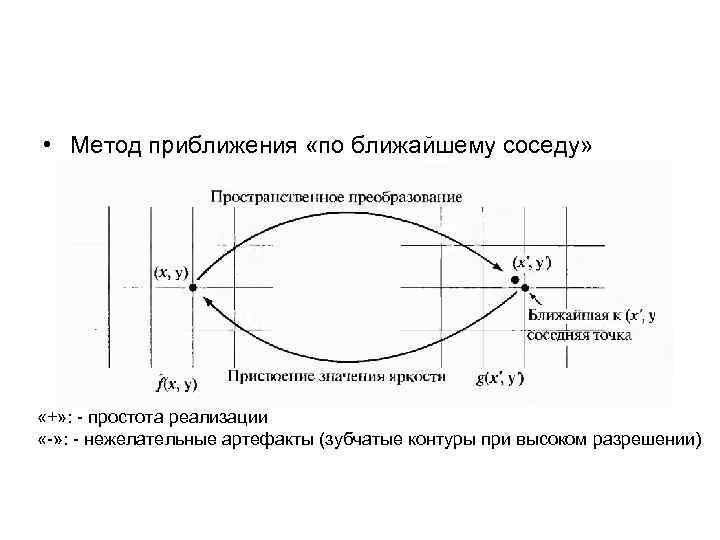
• Метод приближения «по ближайшему соседу» «+» : - простота реализации «-» : - нежелательные артефакты (зубчатые контуры при высоком разрешении)

• Кубические B-сплайны Оценка значения яркости в произвольной точке предполагает построение поверхности вида sin(z)/z так, чтобы она проходила через большое количество соседних точек (n=16) «-» : возрастающая вычислительная сложность «+» : функция непрерывна в узлах сетки, непрерывна и 1 -я производная

• Билинейная интерполяция – 4 ближайших точки Их яркости: v 00, v 01, v 10, v 11 Применяем процедуру одномерной линейной интерполяции по горизонтали и по вертикали: