Тема 4 ДЕДУКТИВНЫЕ ВЫВОДЫ. CИЛЛОГИЗМ

Тема 4 ДЕДУКТИВНЫЕ ВЫВОДЫ. CИЛЛОГИЗМ

Тема 4 1. Вывод и умозаключение. Дедуктивные и недедуктивные выводы 2. Непосредственные выводы 3. Простой категорический силлогизм 4. Прогрессивный и регрессивный полисиллогизм 5. Речевое выражение силлогизмов. Энтимема и эпихейрема

1. Вывод и умозаключение. Дедуктивные и Тема 4 недедуктивные выводы Вывод – это процедура получения нового высказывания из одного или более уже принятых высказываний по определенным правилам. Правило вывода – это предписание, позволяющее из признанных за истинные высказываний получить и признать за истинное некоторое новое высказывание. Например: «Из двух отрицательных посылок не следует никакого заключения» . Важнейшей характеристикой вывода является отношение совместимости между его посылками и заключением. Не может быть выводом, например, связь высказываний, противоречащих другу. Все пираты пьют ром. Пират Фрэнсис Дрейк совсем не пьёт рома. Некоторые пираты все же не пьют ром либо Френсис Дрейк – не пират.

Форма мышления, соответствующая выводу – умозаключение. Языковое выражение, содержащее умозаключение, может не соответствовать его логической структуре. Например, в выражении «Сократ мудр, поскольку знает, что ничего не знает» , заключен вывод: Тот, кто знает, что ничего не знает – мудр Сократ знает, что ничего не знает Сократ мудр

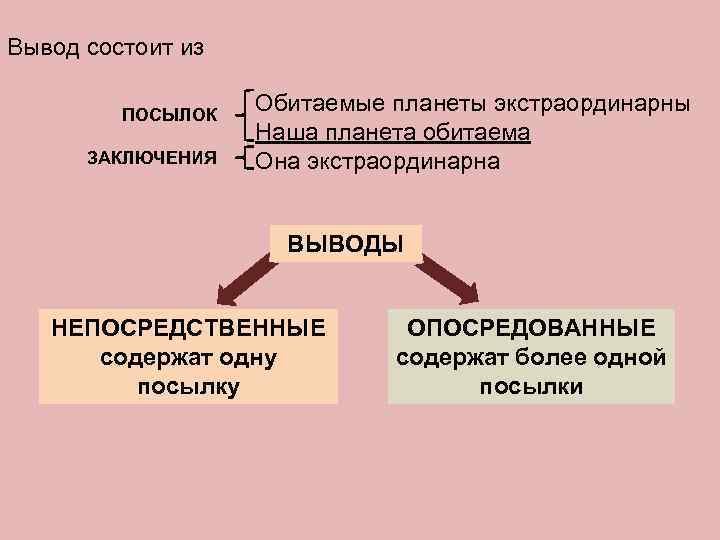
Вывод состоит из ПОСЫЛОК Обитаемые планеты экстраординарны Наша планета обитаема ЗАКЛЮЧЕНИЯ Она экстраординарна ВЫВОДЫ НЕПОСРЕДСТВЕННЫЕ ОПОСРЕДОВАННЫЕ содержат одну содержат более одной посылку посылки

ВЫВОДЫ ДЕДУКТИВНЫЕ ИНДУКТИВНЫЕ ТРАДУКТИВНЫЕ Deductio – Inductio – Traductio – «выведение» «наведение» «перевод» , «перенос» Из общих Из частных Посылки и высказываний заключение равной получают частное получают общее степени общности (например, вывод по аналогии) ВЫВОДЫ ДЕДУКТИВНЫЕ НЕДЕДУКТИВНЫЕ

Тема 4 Дедуктивный вывод: Все мужчины завтракают Некоторые мужчины любят читать газеты Некоторые из тех, кто завтракает, любят читать газеты Индуктивный вывод: У меня всего три брата Мой брат Иван старше меня Мой брат Петр старше меня Мой брат Павел старше меня Все мои братья старше меня Традуктивный вывод: Петр эмоционален Павел эмоционален Петр общителен Павел общителен Петр весел Павел весел Петр любит пошутить Возможно, Павел также любит пошутить

В дедуктивных выводах между посылками (их Тема 4 конъюнкцией) и заключением имеет место отношение следования: всякий раз, когда посылки истинны, заключение тоже истинно. В некоторых случаях отношение между посылками и заключениями характеризуется равнозначностью, т. е. не только из посылок следует заключение, но и из заключения следуют посылки. Дедуктивные выводы – те в которых заключение из посылок следует с необходимостью. (p Λ q)→r В недедуктивных выводах порядок логического следования, как правило, не соблюдается, поэтому заключения носят вероятностный характер

(p Λ q)→r А-посылки В-заключение При определении отношения следования (т. е. дедуктивности вывода) можно использовать понятие логического закона: из конъюнкции посылок A следует заключение В, если и только если выражение A → В – логический закон. Истинность заключения в дедуктивном выводе гарантируется истинностью посылок. Знание, получаемое с его помощью, не может быть более общим, чем то, которое заложено в исходных посылках.

2. Непосредственные выводы Тема 4 Непосредственные выводы – такие, в которых есть только одна посылка, и заключение К ним относятся выводы с применением логических операций обращения, превращения и противопоставления (см. тему «Высказывания» , вопрос 3); а также выводы по логическому квадрату. Например: Выводы из общеутвердительного высказывания А - Все единороги истреблены I - Некоторые единороги истреблены Е - Неверно, что ни один единорог не истреблен О - Неверно, что некоторые единороги не истреблены Вывод из частноутвердительного высказывания I - Некоторые сны понятны Е - Неверно, что ни один сон не понятен

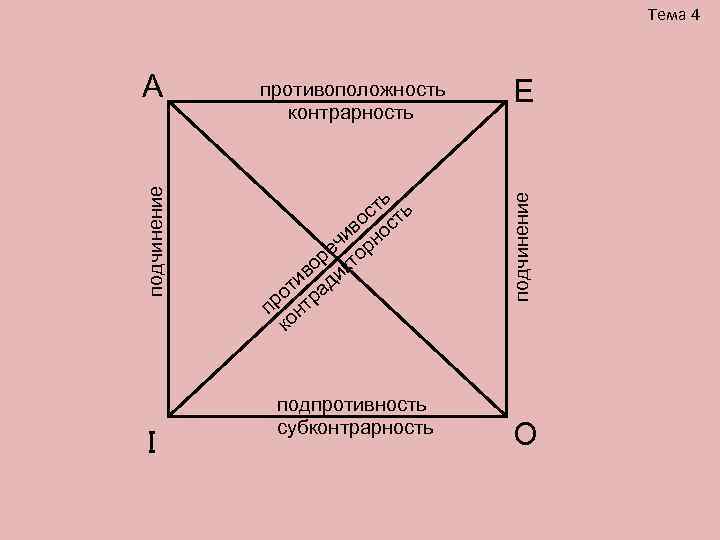
Тема 4 А противоположность Е контрарность подчинение ь подчинение ст ть и во ос еч орн ор кт ив ди т а ро тр п н ко подпротивность субконтрарность I O

Тема 4 Выводы из общеотрицательного высказывания Е - Ни один тщеславный писатель не любит критики О - Некоторые тщеславные писатели не любят критики А - Неверно, что всякий тщеславный писатель любит критику I - Неверно, что некоторые тщеславные писатели любят критику Вывод из частноотрицательного высказывания I - Некоторые афиняне не знакомы с Антисфеном А - Неверно, что все афиняне знакомы с Антисфеном

3. Простой категорический силлогизм (ПКС) Простой категорический силлоги зм (от греч. συλλογισμός – «соединение высказываний» ) – рассуждение, состоящее из двух посылок и одного заключения, т. е. трёх простых атрибутивных высказываний. «Силлогизм… есть речь, в которой если нечто предположено, то с необходимостью вытекает нечто отличное от положенного в силу того, что положенное есть» (Аристотель. Первая аналитика, гл. 1) «Если А сказывается обо всех Б и Б сказывается обо всех В, то А сказывается обо всех В» т. е. Все В есть Б Все Б есть А Все В есть А

Посылки силлогизма разделяются на бо льшую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). Например: Все шаманы умеют камлать (бо льшая посылка) Полштоп – шаман (меньшая посылка) Полштоп умеет камлать (заключение) Аристотель понимает под большей посылкой общее высказывание (со словами «Все» , «Ни один» ), а под меньшей – частное (со словом «Некоторые» ) или единичное (со словами «Этот» , «Данный» ). Если посылки равной степени общности, то большей считается та, что содержит больший термин (наиболее общее имя)

Термины силлогизма – «то, на что распадается посылка» , т. е. «то, что сказывается и то, о чем сказывается» (Аристотель) Термины силлогизма – это имена, входящие в состав посылок и служащие в них субъектом или предикатом Силлогизм содержит три термина: больший (Р), меньший (S) и средний (М) Больший термин (Р) – предикат заключения. Посылка, в которую он входит – большая. Меньший термин (S) – субъект заключения. Посылка, в которую он входит – меньшая. Средний термин (М) – входит в обе посылки и отсутствует в заключении.

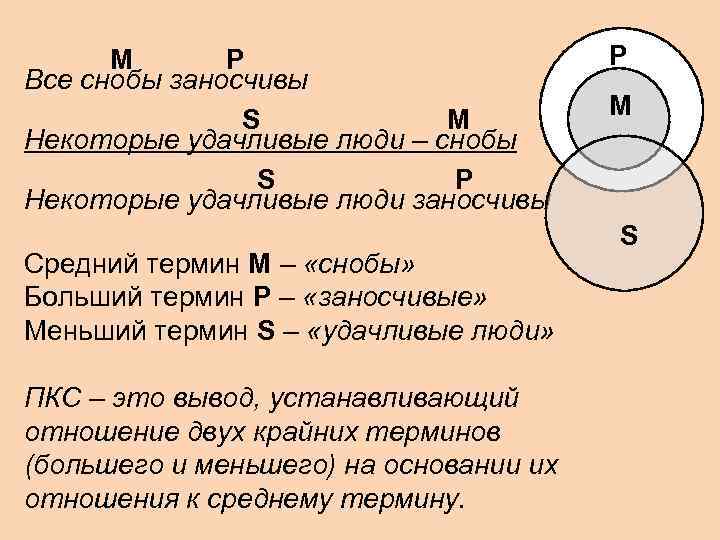
M P P Все снобы заносчивы S M M Некоторые удачливые люди – снобы S P Некоторые удачливые люди заносчивы S Средний термин М – «снобы» Больший термин Р – «заносчивые» Меньший термин S – «удачливые люди» ПКС – это вывод, устанавливающий отношение двух крайних терминов (большего и меньшего) на основании их отношения к среднему термину.

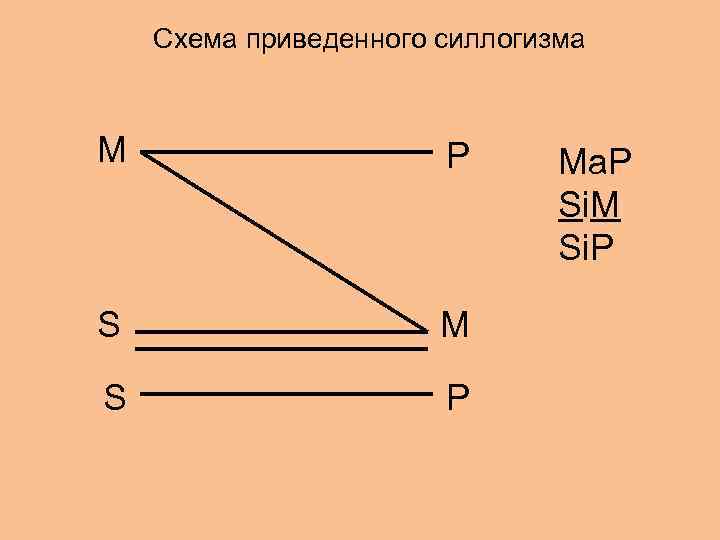
Схема приведенного силлогизма М Р Мa. P Si. M Si. P S М S P

Общие правила ПКС Правила терминов 1. В силлогизме должно быть только три термина. Двух недостаточно, а четвертый – лишний. Нарушение этого правила ведет к ошибке, называемой «учетверение терминов» – разновидности нарушения закона тождества. Тот, у кого есть капитал, может начать бизнес У меня есть капитал моего опыта Я могу начать бизнес

2. Средний термин должен быть распределен хотя бы в одной из посылок Всякое знание полезно Некоторые полезные вещи приятны Некоторое знание приятно? 3. Термин, не распределенный в посылке, не может быть распределен в заключении Всякая рыба может жить в аквариуме Кит – не рыба Кит не может жить в аквариуме?

Правила посылок 4. Из двух частных посылок заключение не следует Некоторые невеселые люди бледны Некоторые бледные люди флегматичны Некоторые невеселые люди флегматичны? 5. Если одна из посылок частная, то и заключение – частное Всякая змея похожа на шланг Некоторые змеи ядовиты Некоторые ядовитые существа похожи на шланг

6. Из двух отрицательных посылок заключение не следует Пельмени не растут на деревьях Вареники – не пельмени Вареники растут на деревьях? 7. Если одна из посылок отрицательная, то и заключение – отрицательное Все тираны закомплексованы Некоторые молодые люди не закомплексованы Некоторые молодые люди – не тираны

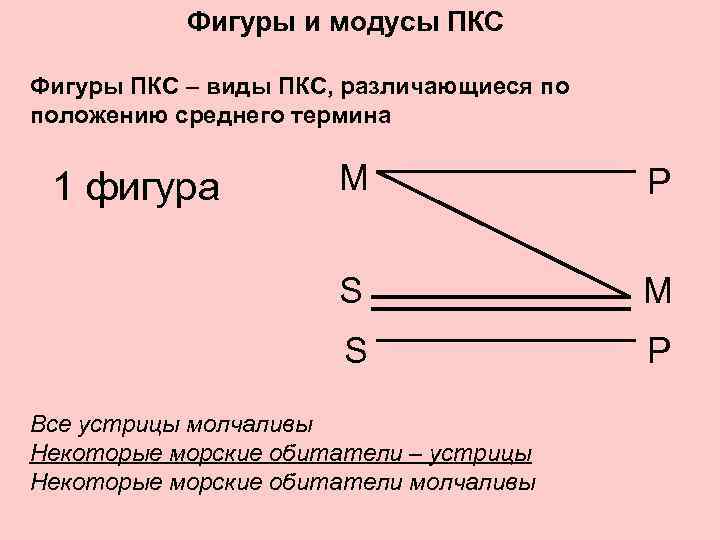
Фигуры и модусы ПКС Фигуры ПКС – виды ПКС, различающиеся по положению среднего термина 1 фигура М Р S М S P Все устрицы молчаливы Некоторые морские обитатели – устрицы Некоторые морские обитатели молчаливы

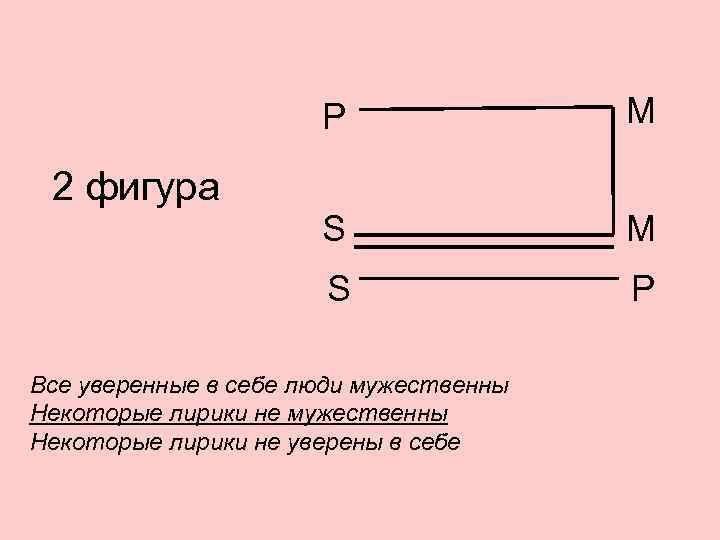
Р М 2 фигура S М S P Все уверенные в себе люди мужественны Некоторые лирики не уверены в себе

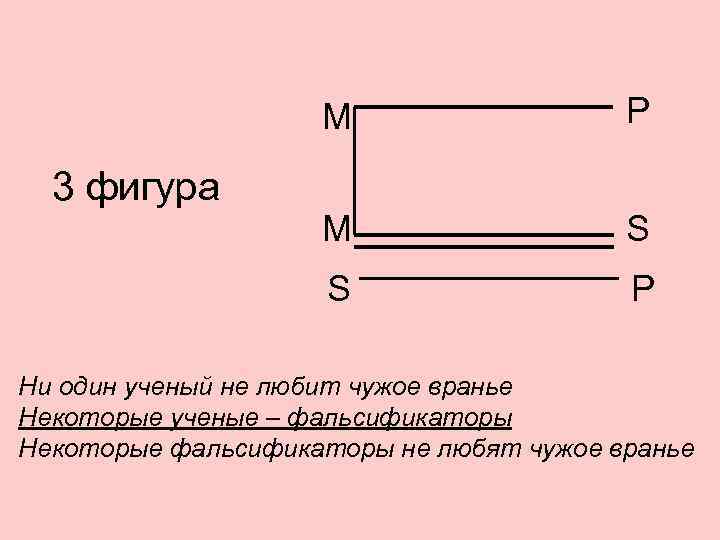
М Р 3 фигура М S P Ни один ученый не любит чужое вранье Некоторые ученые – фальсификаторы Некоторые фальсификаторы не любят чужое вранье

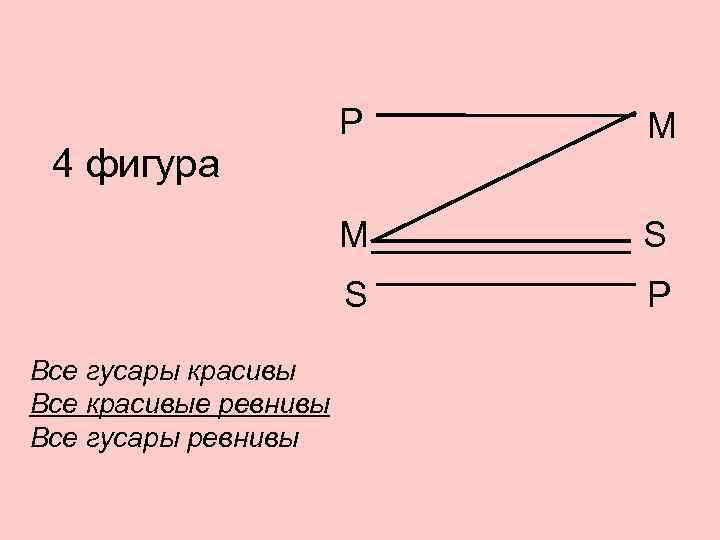
Р М 4 фигура М S P Все гусары красивы Все красивые ревнивы Все гусары ревнивы

Модусы ПКС – разновидности ПКС, различающиеся видами и комбинацией высказываний в посылках Каждая посылка силлогизма может быть одним из четырех высказываний вида А, Е, I, О. Поскольку посылок две и для каждой возможны четыре варианта, число комбинаций простых высказываний в посылках для каждой фигуры будет: 24=16 Следовательно, для четырех фигур число модусов силлогизма будет: 16× 4=64 Из 64 модусов правильными являются только 19. Например, модусы 1 фигуры Barbara, Celarent, Darii, Ferio

19 правильных модусов силлогизма Фигура 1 Barbara Celarent Darii Ferio Фигура 2 Cesare Camestres Festino Baroco Фигура 3 Darapti Disamis Datisi Felapton Bocardo Ferison Фигура 4 Bramantip Camenes Dimaris Fesapo Fresison

4. Прогрессивный и регрессивный полисиллогизм Полисиллогизм – несколько связанных по смыслу простых силлогизмов, в которых заключение предшествующего силлогизма становится посылкой последующего Всякий, кто знает себя, мудр Всякий мудрец интересен в общении Всякий, кто знает себя интересен в общении Интересные в общении люди всегда впечатляют Всякий, кто знает себя, впечатляет Всякий, кто знает себя, гармоничен Некоторые впечатляющие люди гармоничны

Всякий, кто знает себя, мудр Всякий мудрец интересен в общении Всякий, кто знает себя интересен в общении Интересные в общении люди всегда впечатляют Всякий, кто знает себя, впечатляет Полисиллогизм состоит из просиллогизма и эписиллогизма Всякий, кто знает себя, мудр Всякий мудрец интересен в общении Всякий, кто знает себя, интересен в общении Интересные в общении люди всегда впечатляют Всякий, кто знает себя, впечатляет

Прогрессивный полисиллогизм – такой, в котором заключение просиллогизма является большей посылкой эписиллогизма Все добрые люди безобидны Ни один безобидный человек не опасен Ни один добрый не опасен Некоторые добряки – наивны Некоторые наивные люди не опасны

Регрессивный полисиллогизм – такой, в котором заключение просиллогизма является меньшей посылкой эписиллогизма Все ведьмы умеют варить зелье Некоторые ведьмы предпочитают чай Некоторые, предпочитающие чай, умеют варить зелье Все, предпочитающие чай, любят уют Некоторые, любящие уют, умеют варить зелье

Сорит (греч. soros – «куча» ) – сокращенный полисиллогизм, в котором пропущены заключения просиллогизмов Сорит от Л. Кэрролла: 1. Всякий, кто не танцует на туго натянутом канате и не ест пирожков за один пенс, стар. 2. Со свиньями, которые временами испытывают головокружение, обращаются почтительно. 3. Разумный человек, отправляясь в путешествие на воздушном шаре, берет с собой зонтик. 4. Не следует завтракать в присутствии посторонних тому, кто имеет смешной вид и ест пирожки за один пенс. 5. Юные существа, отправляющиеся в путешествие на воздушном шаре, временами испытывают головокружение. 6. Жирные существа, имеющие смешной вид, могут завтракать при посторонних, если только они не танцуют на туго натянутом канате. 7. Ни одно разумное существо не станет танцевать на туго натянутом канате, если оно временами испытывает головокружение. 8. Свинья с зонтиком имеет смешной вид. 9. Все, кто не танцует на туго натянутом канате и с кем обращаются почтительно, жирны. Ответ: Ни один разумный поросенок не отправится путешествовать на воздушном шаре.

5. Речевое выражение силлогизмов. Энтимема и эпихейрема Эллипсисы – выражения с пропущенными, но подразумеваемыми частями Энтимемы (греч. in thymos – в уме) – сокращенные силлогизмы, в которых опускается одна из посылок либо заключение ------- S – P ------- S – P -------

Он же умный ------- Он разберется. S – P Всякий умный человек способен разобраться в чем угодно S – P Он умный Он разберется в чем угодно Все женятся S – P А я не женюсь ------- Все женятся S – P Я – не все Я не женюсь Ни одна научная теория не может объяснить все S – P Теория относительности – всего лишь теория S – P Ни одна научная теория не может объяснить все ------- Теория относительности – всего лишь теория Она не может объяснить все

Методика восстановления и оценки энтимемы на ее состоятельность состоит из следующих шагов: 1. Энтимема записывается в стандартном виде: имеющиеся посылки помещаются над чертой, заключение – под ней. 2. В соответствии с принятой классификацией устанавливается разновидность данного вывода (это может быть категорический силлогизм, условный силлогизм и пр. ). 3. В соответствии с определениями посылок и заключения устанавливается, какая из частей вывода является подразумеваемой. 4. С использованием определений и правил, характерных для данного класса выводов, восстанавливается недостающая часть вывода. 5. Производится анализ восстановленной посылки на соответствие действительному положению дел. Ее ложность означает наличие содержательной ошибки в энтимеме. 6. Производится анализ связей между посылками и заключением на соответствие логическим правилам. Нарушение хотя бы одного из правил свидетельствует о наличии формальной ошибки в энтимеме.

Эпихейрема – (греч. epiheirema «умозаключение» ) – сокращенный полисиллогизм, в котором посылки являются энтимемами Это старьё нельзя выбрасывать: на что-нибудь сгодится Всякая старая вещь может на что-нибудь сгодиться Эта вещь старая Эта вещь может на что-нибудь сгодиться Всякую вещь, которая может сгодиться, нельзя выбрасывать Эту вещь нельзя выбрасывать