Тема 3 Средние величины 1 Понятие средних

Тема 3 Средние величины

1. Понятие средних величин и принципы их применения Средняя величина – это обобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени. Условия правильного применения средних величин Средняя величина должна исчисляться лишь для совокупностей, состоящих из однородных единиц Совокупность, неоднородную в качественном отношении, необходимо разделять на однородные группы и вычислять для них групповые типичные средние, характеризующие каждую из этих групп Средняя величина сглаживает индивидуальные значения и тем самым может элиминировать различные тенденции в развитии (скрыть передовое и отстающее), поэтому средние величины следует дополнять другими показателями

2. Способы определения и виды средних величин Средняя урожайность с одного гектара Средний размер банковского вклада Средние затраты времени на единицу продукции = = =

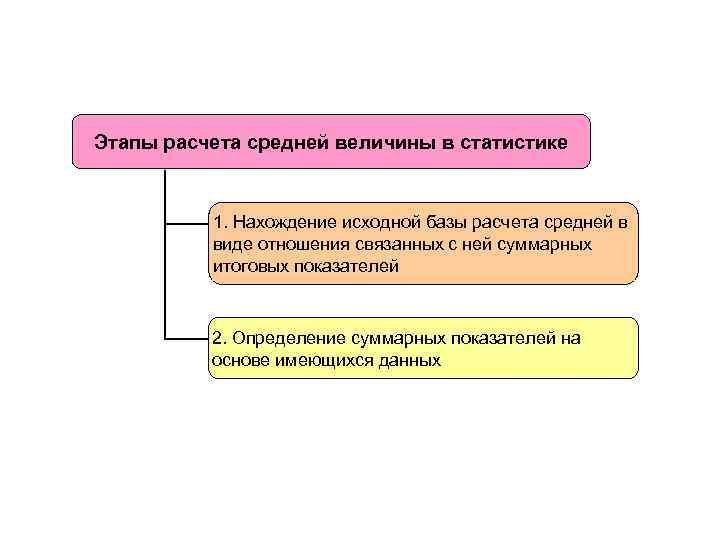Этапы расчета средней величины в статистике 1. Нахождение исходной базы расчета средней в виде отношения связанных с ней суммарных итоговых показателей 2. Определение суммарных показателей на основе имеющихся данных

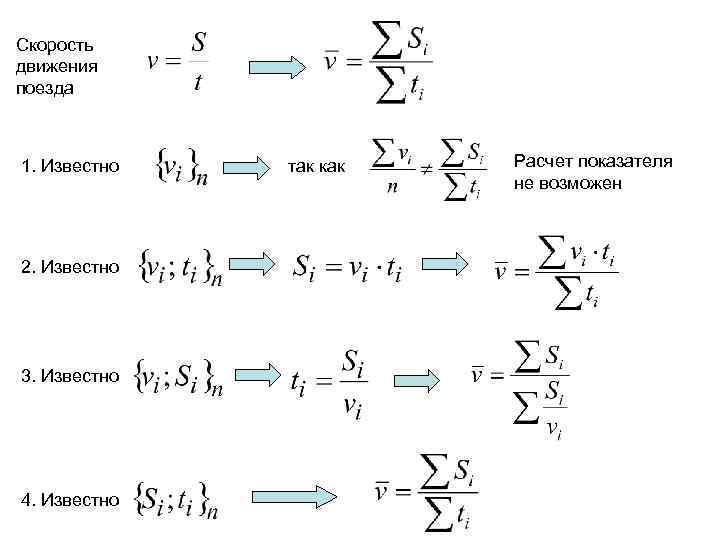Скорость движения поезда 1. Известно 2. Известно 3. Известно 4. Известно так как Расчет показателя не возможен

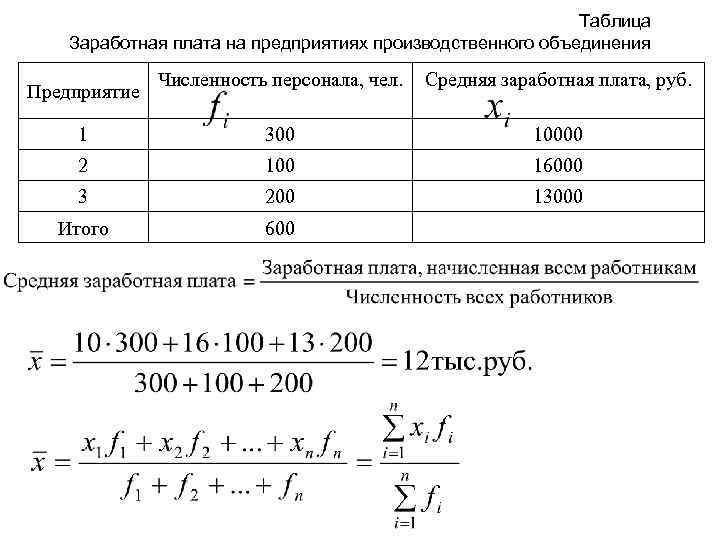Таблица Заработная плата на предприятиях производственного объединения Численность персонала, чел. Средняя заработная плата, руб. 1 300 10000 2 100 16000 3 200 13000 Итого 600 Предприятие

Средняя арифметическая взвешенная Вариант, конкретное значение осредняемого признака Численность (вес) варианта

Таблица Заработная плата на предприятиях производственного объединения Доля численности работников в Предприятие объединении Средняя заработная плата, руб. 1 0, 500 10000 2 0, 167 16000 3 0, 333 13000 Итого 1, 000

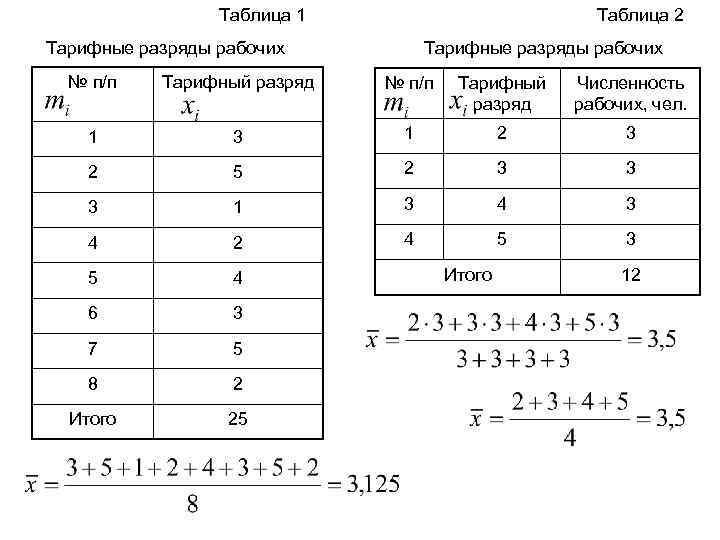Таблица 1 Таблица 2 Тарифные разряды рабочих № п/п Тарифный разряд Численность рабочих, чел. 1 3 1 2 3 2 5 2 3 3 3 1 3 4 2 4 5 3 5 4 6 3 7 5 8 2 Итого 25 Итого 12

Средняя арифметическая простая Вариант, конкретное значение осредняемого признака Число вариантов признака

Свойства средней арифметической 1. Алгебраическая сумма отклонений вариантов от средней арифметической равна нулю: 2. Величина средней арифметической не изменится, если вес каждого варианта умножить (или разделить) на одно и то же число: 3. Если все варианты признака увеличить или уменьшить на одно и то же число или в одно и то же число раз, то так же соответственно изменится и средняя:

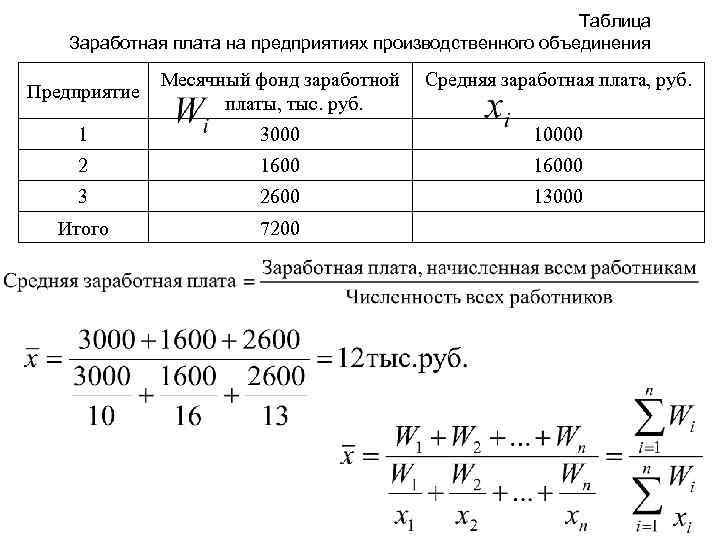Таблица Заработная плата на предприятиях производственного объединения Предприятие Месячный фонд заработной платы, тыс. руб. Средняя заработная плата, руб. 1 3000 10000 2 16000 3 2600 13000 Итого 7200

Средняя гармоническая взвешенная Вариант, конкретное значение осредняемого признака Вес варианта

Средняя гармоническая простая Вес варианта Число вариантов признака

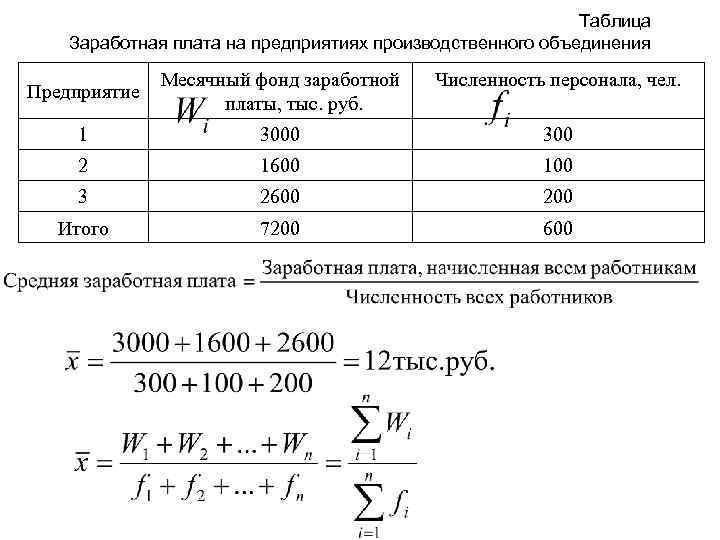Таблица Заработная плата на предприятиях производственного объединения Предприятие Месячный фонд заработной платы, тыс. руб. Численность персонала, чел. 1 3000 300 2 1600 100 3 2600 200 Итого 7200 600

Средняя агрегатная

План выпуска продукции, тыс. руб. Выполнение плана, % Филиал 1 620 108, 2 Филиал 2 930 103, 4 Определить средний процент выполнения плана

Фактически выпущено продукции, тыс. руб. Выполнение плана, % Филиал 1 670, 84 108, 2 Филиал 2 961, 62 103, 4 Определить средний процент выполнения плана

Объем выпуска продукции текущего года, млн. руб. Темп роста объема продукции к предшествующему году, % Филиал 1 360 112, 5 Филиал 2 520 108, 6 Определить средний темп роста