Тема 3 Представление числовой информации с помощью систем

Тема 3 Представление числовой информации с помощью систем счисления 1

Системы счисления (СС) • Для записи о номере и количестве объектов используются числа. • Числа записывают с помощью особых знаковых систем, называемых системами счисления (СС). • Алфавит систем счисления состоит из символов, которые называются цифрами. • Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. • Система счисления – это способ представления чисел и соответствующие ему правила действия над числами. 2

Системы счисления (СС) позиционные непозиционные В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения цифры в записи числа Пример: римская непозиционная система счисления I V X L C D M 1 5 10 50 100 500 1000 CCXXXII=2 сотни + 3 десятка + 2 единицы. ХХХ=30 MCMXCVIII = 1000 + (1000 – 100) + (100 – 10) +5 +1+ 1 +1 = 1998 В римских числах цифры записываются слева направо в порядке убывания. Тогда их значения складываются. Если же меньшая цифра стоит слева от большей, то ее значение вычитается. 3

Непозиционные СС Недостатки непозиционных СС • Нет нуля • Нельзя записывать большие числа (или вводить новые буквы, или много букв рядом) • Нет алгоритмов сложения, деления «в столбик» Примеры использования римской СС • • Часы Размеры на одежде В истории – века Год выпуска некоторых телепрограмм 4

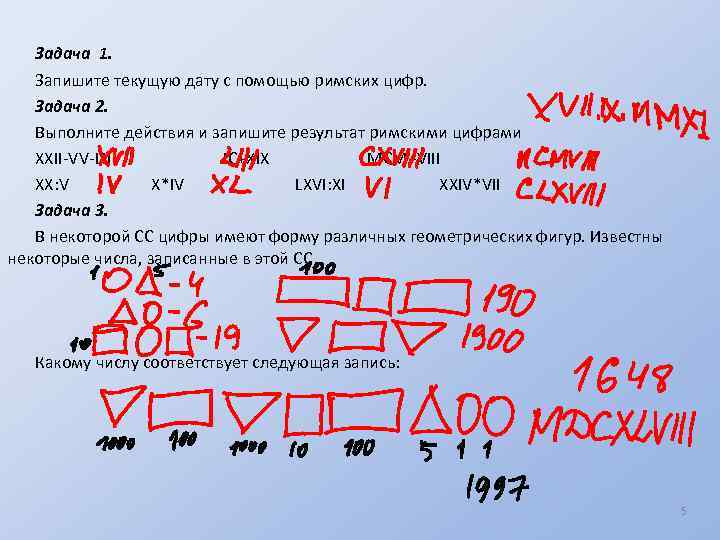Задача 1. Запишите текущую дату с помощью римских цифр. Задача 2. Выполните действия и запишите результат римскими цифрами XXII-VV-LII IC+XIX MCM+VIII XX: V X*IV LXVI: XI XXIV*VII Задача 3. В некоторой СС цифры имеют форму различных геометрических фигур. Известны некоторые числа, записанные в этой СС Какому числу соответствует следующая запись: 5

Позиционные системы счисления (ПСС) В позиционных системах счисления величина, обознача-емая цифрой в записи числа, зависит от ее позиции Первая ПСС – Древний Вавилон - шестидесятеричная XIX век – двенадцатеричная Настоящее время – десятичная, двоичная, восьмеричная, шестнадцатеричная Каждая ПСС имеет определенный алфавит цифр и основание. Основание системы счисления (n) в ПСС равно количеству цифр (знаков в ее алфавите) и определяет, во сколько различаются значения одинаковых цифр, стоящих в соседних позициях числа. При n < 10 используют n арабских цифр, при n ≥ 10 дополнительно к цифрам используют прописные буквы латинского алфавита. При необходимости основание СС указывается нижним индексом: 1011012, 36578, 2 С 9 F 16, 35610 6

Позиционные системы счисления (ПСС) Название СС Двоичная Троичная Восьмеричная Десятичная Шестнадцатеричная Основание n=2 n=3 n=8 n=10 n=16 Алфавит 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15) • Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим. Пример: в 10 -ичной СС имеем разряды единиц, десятков, сотен и т. п. • В системе счисления с основанием q (q-ичная СС) единицами разрядов служат последовательные степени числа q. • q единиц какого-либо разряда образуют единицу следующего разряда. • Для записи числа в q-ичной СС требуется q различных знаков (цифр), изображающих числа 0, 1, …, q – 1. • Запись числа q в q-ичной СС имеет вид 10. 7

Развернутая и свернутая форма записи числа Развернутой формой записи числа называется запись в виде Aq = ±(an-1 qn-1 + an-2 qn-2 + …+ a 1 q 1 + a 0 q 0 + a-1 q-1 + a-2 q-2+ … + a-m q-m ). Здесь Aq – само число, q – основание СС, ai – цифры данной СС, n – число разрядов целой части числа, m – число разрядов дробной части числа. Пример: получить развернутую форму 10 -ичного числа 526, 387. Решение: 526, 38710 = 5*102 +2*101 + 6*100 +3*10 -1 +8*10 -2 +7*10 -3. Вывод: как видно из примера, число в ПСС записывается в виде суммы числового ряда степеней основания (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа. Свернутой формой записи числа называется привычная нам запись: Aq = ±(an-1 an-2 … a 1 a 0 , a-1 a-2 …a-m ). 8

Развернутая и свернутая форма записи числа Десятичная система счисления: Развернутая форма записи числа A 10 = an-1 10 n-1 + an-2 10 n-2 + …+ a 1 101 + a 0 100 + a-1 10 -1 + a-2 10 -2+ … + a-m 10 -m Свернутая форма записи числа A 10 = an-1 an-2 … a 1 a 0 , a-1 a-2 …a-m Двоичная система счисления: Развернутая форма записи числа A 2 = an-1 2 n-1 + an-2 2 n-2 + …+ a 1 21 + a 0 20 + a-1 2 -1 + a-2 2 -2+ … + a-m 2 -m = =an-1 102 n-1 + an-2 102 n-2 + …+ a 1 102 1 + a 0 102 0 + a-1 102 -1 + a-2 102 -2+ … + a-m 102 -m Свернутая форма записи числа A 2= an-1 an-2 … a 1 a 0 , a-1 a-2 …a-m Замечание: в любой СС ее основание записывается как 10 Пример: Получить развернутую форму чисел 1123 1011012 15 FC 16 101, 112 9

Перевод из недесятичной СС в десятичную СС Правило: Если все слагаемые в развернутой форме недесятичного числа представить в десятичной СС и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной СС равное данному. Замечание: умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Пример: Перевести предлагаемые числа в десятичную СС. 1123 1011012 15 FC 16 101, 112 10

Домашнее задание Задача 1. Запишите в развернутой форме числа: 1) A 10 = 125, 34 2) A 8 = 125, 34 3) A 16 = 125, 34 Задача 2. Запишите в десятичной СС числа: 1) A 2=110, 11 2) A 8 = 125, 24 3) A 16 = 12 F, 48 Задача 3. Запишите десятичный эквивалент числа 10101, если считать его написанным во всех СС – от двоичной до девятеричной включительно. Задача 4. Какое минимальное основание может иметь СС, если в ней записаны числа: 110, 23, 67. Задача 5. Запишите число 199910 в римской системе счисления. Задача 6. Во сколько раз увеличатся числа 19, 9910 , 64, 58 , 39, F 16 при переносе запятой на один знак в право? 11

Тема 4 Перевод чисел в другие СС 12

Перевод десятичных чисел в другие СС Перевод целых чисел 1) Основание новой СС выразить в десятичной СС и все последующие действия производить в десятичной СС. 2) Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой СС до тех пор, пока не получим неполное частное, меньшее делителя. 3) Полученные остатки, являющиеся цифрами числа в новой СС, привести в соответствие с алфавитом новой СС. 4) Составить число в новой СС, записывая его, начиная с последнего частного. Пример 1: Перевести число 3710 в двоичную СС. Решение: Для обозначения в записи числа используем символику а 5 а 4 а 3 а 2 а 1 а 0 Пример 2: Перевести десятичное число 315 в 8 -ичную и 16 -ичную СС 13

Перевод десятичных чисел в другие СС Перевод дробных чисел 1) Основание новой СС выразить в десятичной СС и все последующие действия производить в десятичной СС. 2) Последовательно умножать данное число и получаемые дробные части произведений на основание новой СС до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой СС. 3) Полученные целые части произведений, являющиеся цифрами числа в новой СС, привести в соответствие с алфавитом новой СС. 4) Составить дробную часть числа в новой СС, записывая его, начиная с целой части первого произведения. Пример 3: Перевести десятичную дробь 0, 1875 в 2 -ичную, 8 -ичную и 16 -ичную СС. 14

Перевод десятичных чисел в другие СС Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробные части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой СС целая часть отделяется от дробной запятой (точкой). Пример 4: Перевести десятичное число 315, 1875 в 8 -ичную и 16 -ичную СС. 15

Домашнее задание Задача 1. Перевести целые числа из десятичной СС в троичную СС: 1) 12 2) 56 3)121 Задача 2. Перевести десятичные дроби в двоичную СС. В двоичной записи числа оставить 6 знаков. 1) 0, 555 2) 0, 333 3) 0, 453 Задача 3. Перевести смешанные десятичные числа в двоичную и восьмеричную СС, оставив 5 знаков в дробной части нового числа. 1) 21, 5 2) 12, 25 3) 97, 333 16

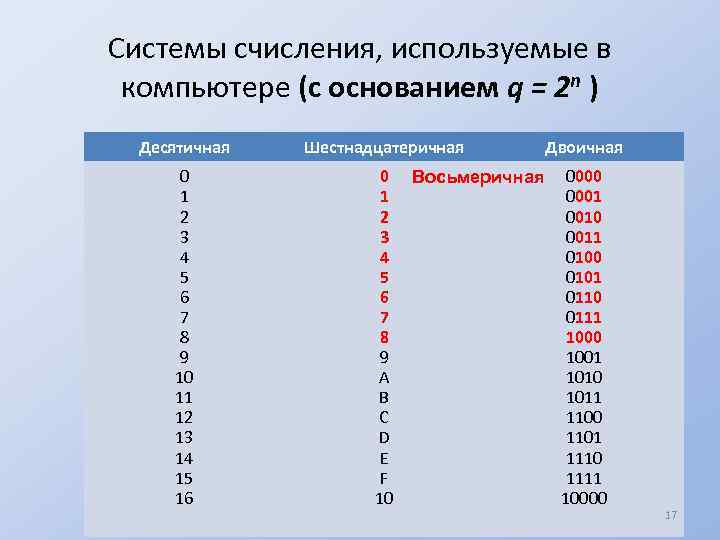Системы счисления, используемые в компьютере (с основанием q = 2 n ) Десятичная Шестнадцатеричная Двоичная 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 A B C D E F 10 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 10000 Восьмеричная 17

Перевод целых двоичных чисел в системы счисления с основанием q = 2 n (4, 8, 16 и т. д. ) • Данное двоичное число разбить справа налево на группы по n цифр в каждой; • Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов; • Рассмотреть каждую группу как n-разрядное двоичное число и записать его соответствующей цифрой в системе СС с основанием q = 2 n • Пример 1: 10101110 18

Перевод дробных двоичных чисел в системы счисления с основанием q = 2 n (4, 8, 16 и т. д. ) • Данное двоичное число разбить слева направо на группы по n цифр в каждой; • Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов; • Рассмотреть каждую группу как n-разрядное двоичное число и записать его соответствующей цифрой в системе СС с основанием q = 2 n • Пример 2: 0, 1010111 19

Перевод смешанных двоичных чисел в системы счисления с основанием q = 2 n (4, 8, 16 и т. д. ) • Целую и дробную части данного двоичного числа начиная от запятой разбить на группы по n цифр в каждой; • Если в последней правой и левой группах окажется меньше n разрядов, то их надо дополнить соответственно справа и слева нулями до нужного числа разрядов; • Рассмотреть каждую группу как n-разрядное двоичное число и записать его соответствующей цифрой в системе СС с основанием q = 2 n • Пример 3: 10101110, 1010111 20

Перевод произвольных чисел из СС с основанием q = 2 n (4, 8, 16 и т. д. ) в двоичную СС Необходимо каждую цифру исходного числа заменить ее n-разрядным эквивалентом в двоичной системе счисления Пример 4: 15 FC 16 Проверка: переведем оба числа в десятичную СС 21

Перевод произвольных чисел из одной СС с основанием q 1= 2 n 1 в другую СС с основанием q 2=2 n 2 Для этого необходимо сначала перевести исходное число из СС с основанием q 1 в двоичную СС, а затем полученное число перевести из двоичной СС в СС с основанием q 2. Пример 5: 57 FC, 37 А 16 перевести в 8 -ичную СС. 22

Задача 1. Перевести двоичное число в шестнадцатеричную СС 110111101011112 = Задача 2. Перевести смешанное двоичное число в шестнадцатеричную СС 1011101, 101112 = Задача 3. Перевести смешанное двоичное число в восьмеричную СС 1011101, 101112 = Задача 4. Перевести восьмеричное число в шестнадцатеричную СС 135, 568 = Задача 5. Перевести восьмеричное число в четверичную СС 135, 568 = 23

Домашнее задание Задача 1. Перевести целые и дробные числа из двоичной СС в восьмеричную СС: 1) 1100001101011 2) 1000001010 3)0, 1100011 4)0, 1001110001111 Задача 2. Перевести целые и дробные числа из двоичной СС в шестнадцатеричную СС: 1) 1100001101011 2) 1000001010 3)0, 1100011 4)0, 1001110001111 Задача 3. Перевести целые, дробные и смешанные числа из восьмеричной СС в двоичную СС: 1) 256 2) 127 3)0, 344 4)240, 0251 Задача 4. Перевести целые и дробные числа из шестнадцатеричной СС в двоичную СС: 1) 1 АС 8 2) 0, F 6 C 7 3)0, E 240 D 4)AF, FA 1 C Задача 5. Перевести числа из шестнадцатеричной СС восьмеричную СС. 1) 2 F 1, 5 2) 12, 25 3) 97, 3 D 3 24

Арифметика в позиционных системах счисления Любая позиционная СС определяется основанием СС, алфавитом и правилами выполнения арифметических операций. В основе правил арифметики лежат таблицы сложения и умножения однозначных чисел. Например, в пятеричной СС эти таблицы имеют вид: + 0 1 2 3 4 0 0 1 2 3 4 10 2 2 3 4 10 11 3 3 4 10 11 12 4 4 10 11 12 13 * 1 2 3 4 1 1 2 3 4 2 2 4 11 13 3 3 11 14 22 4 4 13 22 31 Примеры: 25

Домашнее задание Задача 1. Составьте таблицы сложения и умножения в троичной СС и вычислите: 1) 12 + 22 2) 211 – 21 3) 21* 2 4) 11: 2 Задача 2. Составьте таблицы сложения и умножения в двоичной СС и вычислите: 1) 1101 + 1011 2) 10101 - 1111 3)111*11 4)1110 : 10 Задача 3. Составьте таблицу сложения в восьмеричной СС и вычислите: 1 1) 256 + 333 2) 127 – 65 3)344 + 771 4)270 - 251 Задача 4. Составьте таблицу сложения в шестнадцатеричной СС и вычислите: 1) 1 АС 8 - ССС 2) F 6 C 7 + 39 3)E 240 – 111 4)AF + FA 1 C 26