ТЕМА 3 ОПИСАТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ ИССЛЕДУЕМОЙ СОВОКУПНОСТИ СРЕДНИЕ ВЕЛИЧИНЫ

ТЕМА 3. ОПИСАТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ ИССЛЕДУЕМОЙ СОВОКУПНОСТИ: СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИ

ВОПРОС 1. ОПРЕДЕЛЕНИЕ, ВИДЫ И ФОРМЫ СРЕДНИХ ВЕЛИЧИН СТАТИСТИКА ИЗУЧАЕТ МАССОВЫЕ ЯВЛЕНИЯ. ¡ КАЖДОЕ ИЗ ТАКИХ ЯВЛЕНИЙ ОБЛАДАЕТ КАК ОБЩИМИ ДЛЯ ВСЕЙ СОВОКУПНОСТИ, ¡ ТАК И ОСОБЕННЫМИ, ИНДИВИДУАЛЬНЫМИ СВОЙСТВАМИ. ¡

¡ Для изучения общих, типических характеристик совокупности применяется метод средних величин. ¡ Для изучения степени различий признаков совокупности – методы измерения вариации.

С помощью метода средних статистика решает множество задач Главное значение средних величин состоит в их обобщающей функции, ¡ т. е. замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. ¡

ФОРМЫ средних Виды и формы средних ВИД средних в зависимости от вида осредняемого признака ПРОСТАЯ СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ СРЕДНЯЯ КВАДРАТИЧЕСКАЯ СРЕДНЯЯ КУБИЧЕСКАЯ СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ СРЕДНЯЯ ГАРМОНИЧЕСКАЯ ВЗВЕШЕННАЯ ∑ xi X = -----n ∑ xi ∑xjfj X= -----∑f j ∑ xj 2 2 fj X =√ -----n X=√ -----∑fj ∑ xi 3 X =√ -----n ∑ x j 3 f j X=√ -----∑fj 3 n 3 ∑ fj X =√ x 1 x 2 x 3 … xn X =√ x 1 f 1 x 2 f 2 x 3 f 3…xj fj n Х = -----∑ 1/xi ∑fj Х = -----∑fj/xj

Различие между формами средних обусловлено тем, что при обобщении различных признаков социальноэкономических явлений бывает необходимым сохранение неизменными различных параметров исходной информации ¡ (сумму квадратов исходных величин, произведение индивидуальных величин, сумму величин, обратных индивидуальным значениям признака) ¡

Средняя арифметическая ¡ ¡ ¡ Это такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Среднее слагаемое – деление поровну между всеми единицами совокупности Средняя продолжительность жизни, средняя зарплата, среднее число студентов в группе

Виды средних Существование двух видов средней – простой и взвешенной – обусловлено существованием признаков разных видов. ¡ В зависимости от вида признаков (первичного или вторичного) средние могут быть рассчитаны как простые и взвешенные. ¡

Виды средних ¡ ¡ Для расчета средних первичных признаков применяется простая средняя. Для расчета средних вторичных признаков применяется взвешенная средняя. Взвешенная средняя м. б. рассчитана и для первичных признаков, если они представлены в сгруппированном виде. Несгруппированные данные осредняются по простой средней.

При расчете простых средних учитывается значение только осредняемого признака. ¡ При расчете взвешенных средних, наряду со значением осредняемого признака, в расчет включаются значения другого связанного с ним признака – признака-веса. ¡

Признак -вес Название вес означает тот факт, что разные значения признака имеют неодинаковую «важность» (значимость) при расчете средних (тем самым учитывается влияние структуры совокупности) ¡

Способы расчета взвешенных средних ¡ 1. Как соотношение двух сумм значений, по признакам, определяющим содержание вторичного признака: Рентабельность отдельного вида продукции = прибыль от реализации продукции отдельного вида / затраты на ее производство (полная себестоимость) * 100, % Р = П/З *100, % Р ср. = ∑ Пi / ∑ Зi

Способы расчета взвешенных средних ¡ ¡ 2. на основе отдельных значений осредняемого вторичного признака и признака-веса. РЕНТАБЕЛЬНОСТЬ ОТД ВИДОВ ПРОДУКЦИИ Р 1 Р 2 Р 3 … Рn ЗАТРАТЫ НА ПРОИЗВОДСТВО ОТД ВИДОВ ПРОДУКЦИИ З 1 З 2 З 3 … Зn P ср = ∑ Рi Зi / ∑ Зi = ∑ Пi / ∑ Зi

Условия использования средних ¡ ¡ Совокупность, по которой проводится обобщение, д. б. однородной. При расчете необходимо учитывать своеобразие и взаимосвязь признаков и использовать средние в сочетании с другими статистическими показателями.

Условия использования средних ¡ ¡ ¡ Порядок расчета средних сохраняется независимо от уровня обобщения: если Урожайность = валовой сбор/посевная площадь, то и средняя урожайность = ∑ВС/∑ПП, а не средняя урожайность = ∑У/n В искл случаях, когда не известен признак-вес, средняя величина вторичного признака м. б. определена по СРЕДНЕЙ ПРОСТОЙ.

ПОНЯТИЕ О СТЕПЕННОЙ СРЕДНЕЙ ¡ ¡ ¡ ВСЕ ВИДЫ СРЕДНИХ ПРИНАДЛЕЖАТ К ОБЩЕМУ ТИПУ СТЕПЕННЫХ СРЕДНИХ. РАЗЛИЧАЮТСЯ ОНИ ЛИШЬ ПОКАЗАТЕЛЕМ СТЕПЕНИ “k”. Степенная средняя степени есть корень k–той степени из частного от деления суммы индивидуальных значений признака в k–той степени на число индивидуальных значений (число единиц совокупности):

ПОНЯТИЕ О СТЕПЕННОЙ СРЕДНЕЙ k ∑ xi k X ср. =√ -----n ¡ ¡ ¡ K=1 – средняя арифметическая K=2 - средняя квадратическая K=-1 – средняя гармоническая K=0 – средняя геометрическая Чем больше показатель степени k, тем больше х ср.

Правило мажорантности средних ¡ Х гарм ≤ Х геом ≤ Х арифм≤ Х квадр ≤ Х кубич

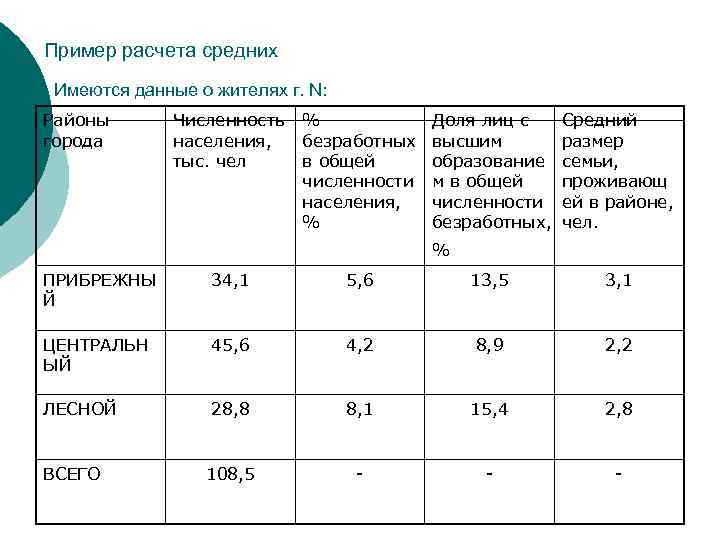Пример расчета средних Имеются данные о жителях г. N: Районы города Численность населения, тыс. чел % безработных в общей численности населения, % Доля лиц с высшим образование м в общей численности безработных, Средний размер семьи, проживающ ей в районе, чел. % ПРИБРЕЖНЫ Й 34, 1 5, 6 13, 5 3, 1 ЦЕНТРАЛЬН ЫЙ 45, 6 4, 2 8, 9 2, 2 ЛЕСНОЙ 28, 8 8, 1 15, 4 2, 8 108, 5 - - - ВСЕГО

АЛГОРИТМ ВЫБОРА ВИДА СРЕДНЕЙ ¡ ¡ ПЕРВИЧНЫЙ ПРИЗНАК - ПРОСТАЯ СРЕДНЯЯ ВТОРИЧНЫЙ ПРИЗНАК – ВЗВЕШЕННАЯ СРЕДНЯЯ – ГАРМОНИЧЕСКАЯ ИЛИ АРИФМЕТИЧЕСКАЯ

ПОРЯДОК ПОСТРОЕНИЯ ВЗЕШЕННОЙ СРЕДНЕЙ ¡ ¡ ¡ 1. ОПРЕДЕЛЯЕТСЯ ЛОГИЧЕСКАЯ ФОРМУЛА ПОСТРОЕНИЯ СРЕДНЕЙ ВЕЛИЧИНЫ. 2. СРЕДНЯЯ ОПРЕДЕЛЯЕТСЯ КАК СООТНОШЕНИЕ ДВУХ СУММ 3. В ЗАВИСИМОСТИ ОТ ТОГО, ЧТО НЕИЗВЕСТНО, ЧИСЛИТЕЛЬ ИЛИ ЗНАМЕНАТЕЛЬ ДРОБИ, РАССЧИТЫВАЕТСЯ: -СРЕДНЯЯ ГАРМОНИЧЕСКАЯ – ЕСЛИ НЕИЗВЕСТЕН ЗНАМЕНАТЕЛЬ -СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ-ЕСЛИ НЕИЗВЕСТЕН ЧИСЛИТЕЛЬ