Тема 3 Эластичность Учебные вопросы Прямая эластичность спроса

Тема 3 «Эластичность» Учебные вопросы: Прямая эластичность спроса по цене Перекрестная эластичность спроса по цене Эластичность спроса по доходу Эластичность предложения по цене

1. Прямая эластичность спроса по цене n n Эластичность — это мера чувствительности одной переменной к изменению другой, или число, которое показывает процентное изменение одной переменной в результате изменения другой переменной. Ценовая эластичность запрашиваемого количества блага, или, иначе говоря, прямая эластичность спроса по цене (ή — греческая буква «эта» ), определяется как процентное изменение объема спроса, поделенное на процентное изменение цены, причем объем спроса является зависимой переменной величиной.

n Изобразим это в формализованном виде: (3. 1) n n где Δ — символ (греческая буква «дельта» ), обозначающий изменение; ΔQ — изменение спроса; Δ Р — изменение цены. Существуют два метода вычисления коэффициента эластичности: 1) определение дуговой и 2) точечной эластичности.

n n n Дуговой эластичностью называется эластичность между двумя точками линии спроса или предложения. Определение дуговой эластичности методом центральной точки. (3. 1 б)

n n n Точечная эластичность. Теперь рассмотрим понятие точечной эластичности (или эластичности в точке). Точечная эластичность характеризует относительное изменение объема спроса при бесконечно малом изменении цены. (3. 2)

n n эластичность в точке прямой линии спроса равна либо отношению длин отрезков, которые проекция данной точки отсекает на осях, либо отношению отрезков самой линии. Таким образом: если OD = DC, то ή = 1; если OD >DC, то ή > 1; если OD < DC, то ή < 1.

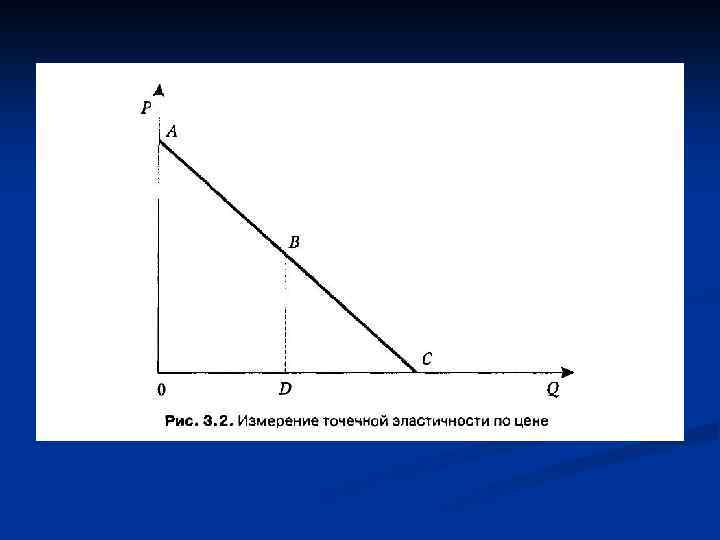
n Понятно, что эластичность в точке А стремится к бесконечности (∞), а в точке С равна нулю (0), а в точке В мы имеем единичную эластичность. На отрезке АВ линия спроса эластична, а на отрезке ВС неэластична (рис. 3. 3).

n n Не следует отождествлять наклон линии с эластичностью Мы знаем, что формула эластичности состоит из двух сомножителей: (Δ Q/ Δ P) и (Р/ Q). Первый из этих сомножителей постоянен, так как он определяет наклон линии. Но зато второй сомножитель (Р / Q) меняется в зависимости от положения точки на линии. Поэтому все наклонные прямые спроса изменяют свою эластичность от точки к точке и судить только по наклону прямой линии об ее эластичности не следует.

n n n Все прямые наклонные линии спроса с отрицательным наклоном имеют разную эластичность в разных точках. Лишь у равнобедренной гиперболы коэффициент эластичности равен единице в любой ее точке. Если изменение цены не вызывает никакого изменения спроса, то мы имеем дело с нулевой эластичностью спроса: ή = 0. Напротив, если любое бесконечно малое изменение цены вызывает бесконечное увеличение спроса, то налицо спрос с бесконечной эластичностью: ή = ∞. Вертикальная прямая спроса обладает нулевой эластичностью, а горизонтальная — бесконечной по величине эластичностью (рис. 3. 4)

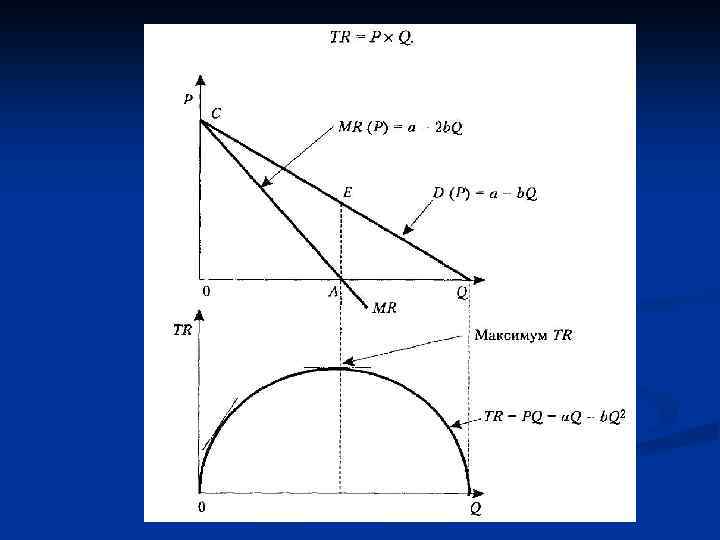
n Изменение эластичности по цене связано с совокупной (общей) выручкой (рис. 3. 5). Совокупная (общая) выручка (TR — total revenue) равна произведению количества проданной продукции (Q), умноженной на цену единицы продукции (Р):

Как видно на рис. 3. 5, при максимальной цене спроса (ή = ∞) общая выручка равна нулю. Затем, с понижением цены (при ή > 1), выручка фирмы увеличивается, достигает своего максимума (при ή = 1); дальнейшее понижение цены (при ή < 1) лишь продолжает снижать выручку, доведя ее до 0 при Р = О (ή=0). n Если мы начнем рассматривать нашу модель с нулевой цены (Р = 0), увеличивая ее, то процесс будет протекать в обратной последовательности n

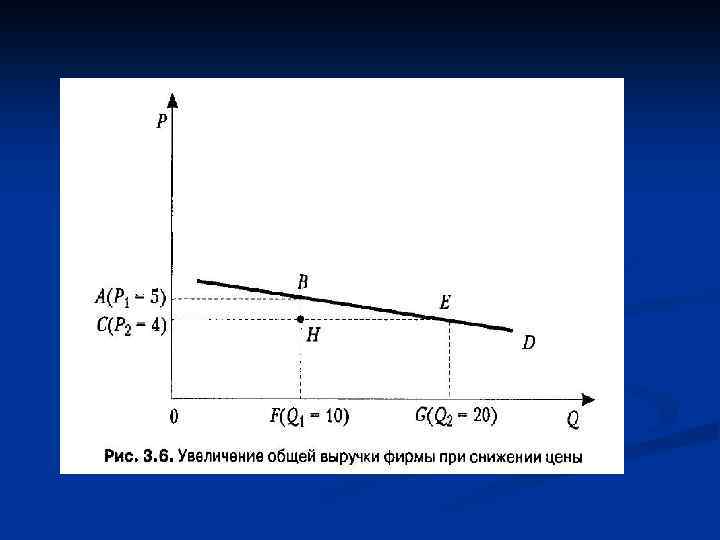
Выведем теперь формулу функциональной зависимости между эластичностью спроса, изменением цены и выручкой продавца. Обратимся для этого вновь к рис. 3. 6. При снижении цены с Р 1, до Р 2 величина спроса увеличилась с Q 1, до Q 2. n Поэтому, чтобы оценить изменение выручки, необходимо из величины площади прямоугольника АВНС вычесть величину площади HEGF: n

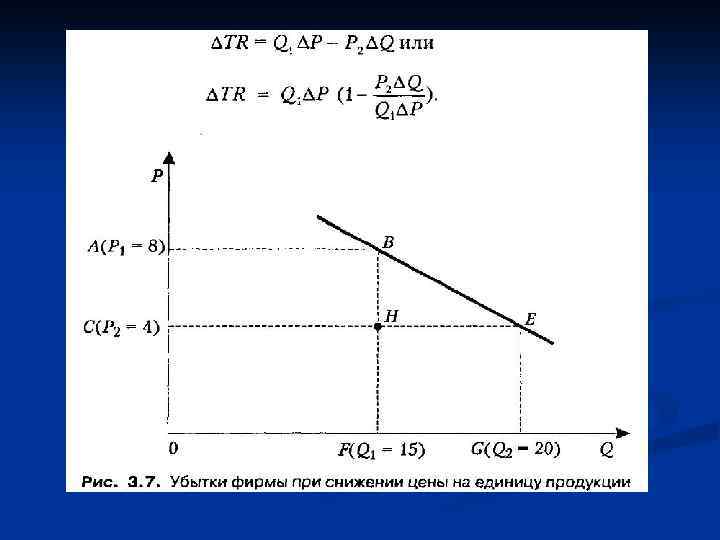
n n n Обратим внимание, что выражение P 2ΔQ/Q 2ΔP представляет собой не что иное, как коэффициент прямой эластичности спроса по цене (на базе минимальных значений цены и объема). Поэтому: ΔTR = Q 1ΔP (1 – ή) (3. 3) Из данной формулы наглядно видно, что при ή=1 значение формулы 3. 3 равно нулю и приращение выручки продавца равно нулю как при увеличении, так и при уменьшении цены

n Прирост общей выручки в результате продажи дополнительной единицы товара называют предельной выручкой {MR - marginal revenue):

Правила прямой эластичности спроса по цене n Правило № 1. Чем насущнее потребность, удовлетворяемая товаром, тем ниже эластичность спроса на этот товар. Другими словами, товар настолько необходим покупателю, что он согласен купить его практически по любой цене. n

n n n Правило № 2. Спрос становится более эластичным на долгосрочных отрезках времени. Правило № 3. Эластичность спроса падает при увеличении насыщенности потребности в том или ином благе. Правило № 4. Эластичность спроса на товар увеличивается по мере роста числа товаровзаменителей. В этом случае поле выбора потребителя расширяется. Потребитель более не привязан к одному виду товара. При отсутствии заменителей спрос обычно неэластичен.

Правило № 5. Агрегированность товарной продукции снижает эластичность спроса (агрегированной группы в целом). n Правило № 6. Эластичность спроса тем выше, чем больший удельный вес товара в расходах потребителя при условии высокой значимости данного товара для потребителя. n

Правило № 7. Эластичность спроса зависит от универсальности использования данного товара. n Правило № 8. Эластичность спроса зависит от психологии потребителя. И это учитывают в своей деятельности фирмы. n Здесь следует упомянуть о моде. Ценовая эластичность спроса на особо модные товары резко снижается. n

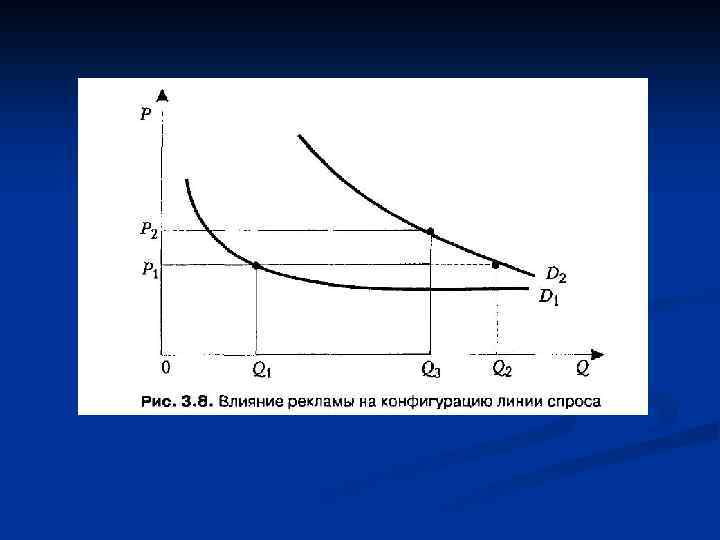
Реклама пытается убедить покупателя, что такой-то товар имеет выдающиеся свойства. Это приводит к следующим последствиям: n • линия спроса сдвигается вправо (если реклама привлечет внимание покупателей и возбудит у них желание купить данный товар); n • эластичность линии спроса снижается (если реклама убедит покупателя, что данный товар является наилучшим и не имеет полноценных субститутов). n

2. Перекрестная эластичность спроса по цене n Перекрестная эластичность спроса по цене определяется как процентное изменение количества запрашиваемого продукта 1, поделенное на процентное изменение цены продукта 2. При этом цена продукта 1 становится условием ceteris paribus.

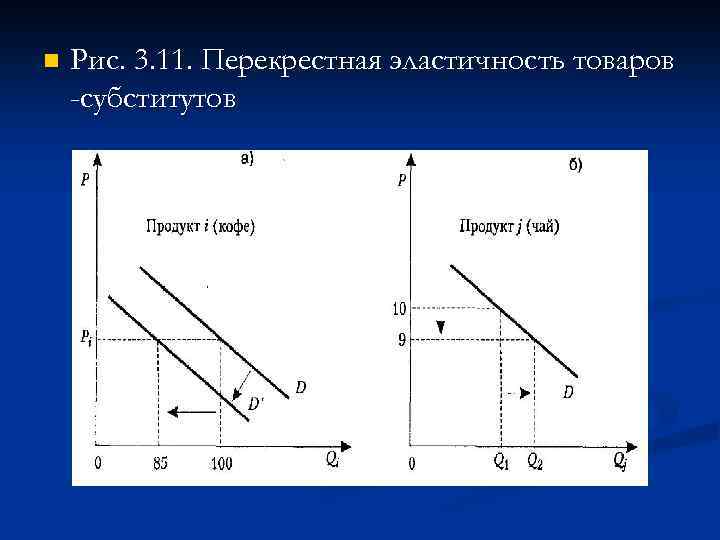
n Рис. 3. 11. Перекрестная эластичность товаров -субститутов

n Рассмотрим пример перекрестной эластичности субститутов (рис. 3. 11). Допустим, это кофе (продукт i) и чай (продукт j). Предположим, что цена чая (продукта j) упала с 10 до 9 р. Это вызвало снижение потребления кофе (i) со до 85 ед. Подсчитаем дуговую перекрестную эластичность (по формуле 3. 1, б):

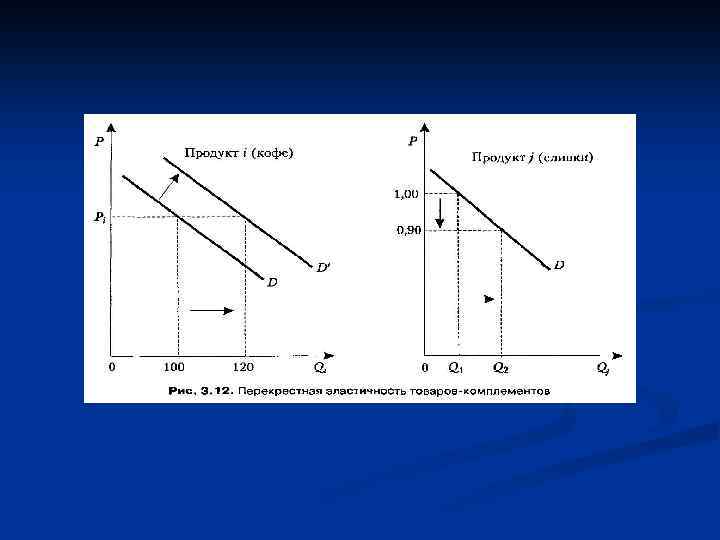
Если цена продукта j снижается, а объем спроса на продукт i возрастает (ή 1<0), то данные виды продукции являются комплементарными (взаимодополняющими). n Рассмотрим это на конкретном примере (продукт i - кофе, продукту j - сливки). Ситуация проиллюстрирована на рис. 3. 12. Предположим, что падение цены на сливки привело к увеличению потребления кофе на 20%. Величина перекрестной эластичности в данном случае равна (по формуле 3. 16): n

n n Перекрестная эластичность спроса может быть асимметричной. Это значит, что встречаются ситуации, когда, к примеру, увеличение цены товара j приведет к снижению спроса товара i, но, с другой стороны, увеличение цены товара i может не изменить спроса на товар j или величина изменения оказывается совершенно иной. Эластичностью ценовых ожиданий (е) называется относительное изменение ожидаемой цены экономического блага, поделенное на относительное изменение текущей цены данного блага.

3. Эластичность спроса по доходу n Эластичность спроса по доходу (греческая бу «мю» ) — это процентное изменение объема с (Q), поделенное на процентное изменение дох потребителя. I). (

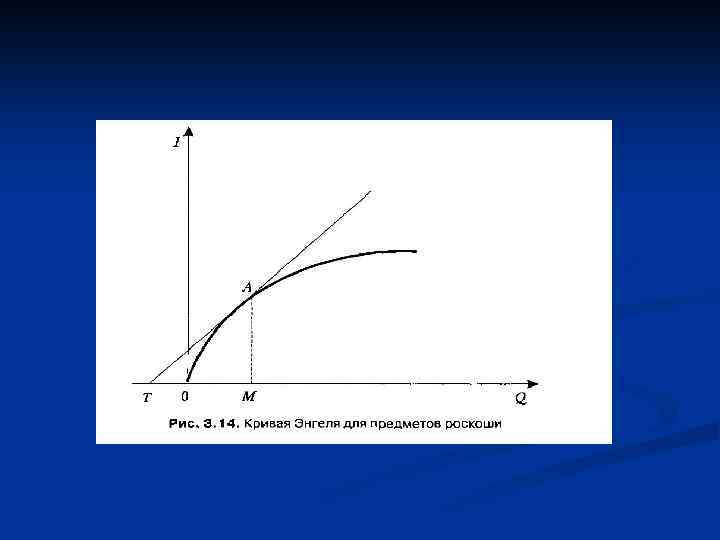
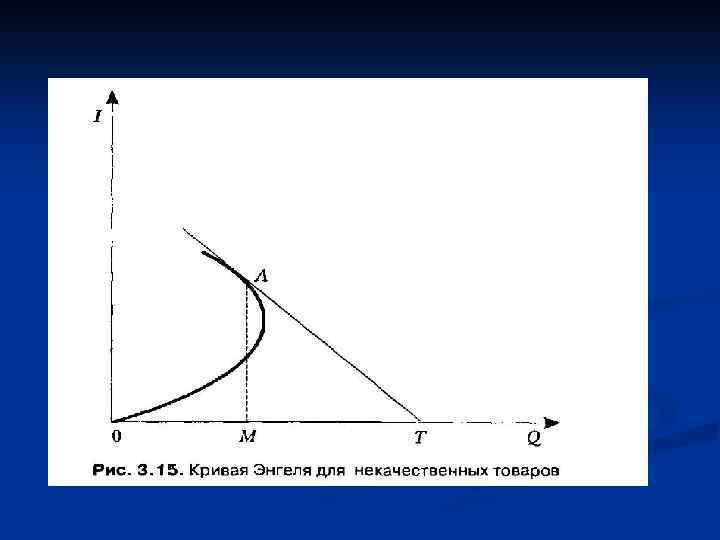
n Эта формула полезна при определении эффекта, оказываемого на спрос, для определенного блага при изменении только дохода. Если данный коэффициент положителен (μ > 0), то мы имеем дело с «нормальным» , «стандартным» , или «качественным» , товаром. Если коэффициент отрицателен (μ < 0), то такой товар условно называют «некачественным» . Если μ > 1, то говорят, что эластичность спроса по доходу высока. Спрос на эти товары опережает рост доходов. Для них не существует пределов насыщения. Товары с высокой эластичностью спроса по доходу принято условно называть «предметами роскоши» ( «luxuries» ). Это название часто условно, так как помимо собственно драгоценностей сюда относят товары длительного пользования. С другой стороны, если μ < 1, то считается, что эластичность спроса по доходу низка.

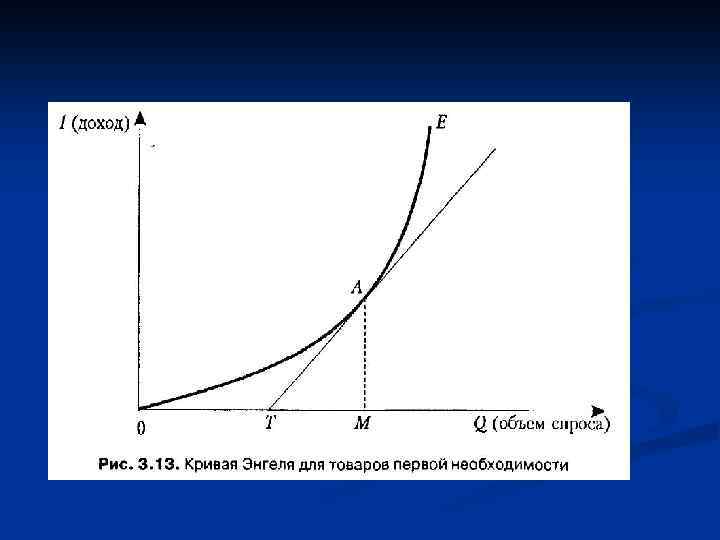
n Наклон касательной определяется отношением AM / ТМ. Отношение дохода к спросу выражается отношением AM/0 М. Поэтому эластичность спроса по доходу (формула 3. 7 а) может быть выражена следующим образом:

4. Эластичность предложения по цене n Коэффициент ценовой эластичности предложения (v — греческая буква «ни» ) определяется как процентное изменение количества предлагаемой продукции к процентному изменению цены:

В большинстве случаев коэффициент ценовой эластичности предложения (в отличие от эластичности спроса) имеет знак плюс, так кривые предложения чаще всего характеризуются положительным наклоном. n Если коэффициент ценовой эластичности предложения больше единицы (v > 1), то кривая предложения эластична. Если v = 1, то кривая предложения имеет единичную эластичность, и если v < 1, то предложение неэластично. n

n Любопытно отметить, что любая прямая линия предложения, проходящая через начало координат, обладает ценовой эластичностью, равной 1. Для доказательства этого положения обратимся к рис. 3. 17. Наклон кривой S 1 равен отношению АВ/В 0. Согласно формуле ценовой эластичности, имеем:

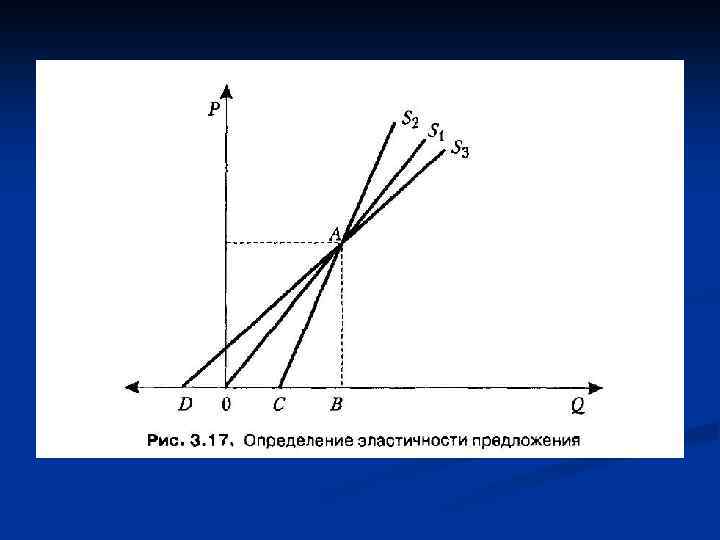
n Тогда, согласно формуле (3. 8), коэффициент ценовой эластичности предложения для линии S 1 равен:

n Подобным способом можно продемонстрировать, что любая прямая предложения, пересекающая ценовую ось (ординат), обладает коэффициентом ценовой эластичности, большим единицы (v>1), а прямая линия предложения, пересекающая количественную ось (абсцисс), имеет коэффициент ценовой эластичности v<1. Так, для линии S 3 (рис. 3. 17), наклон может быть измерен как отношение АВ/DB (ΔP/ΔQ). Тогда ΔQ/ΔP = DB/АВ.

n. И коэффициент ценовой эластичности предложения для линии S 3 равен:

n Для прямой предложения S 2 (рис. 3. 17. ) наклон задан отношением АВ/СB т. е.

n При этом коэффициент ценовой эластичности предложения линии S 2 равен:

n Данные выводы справедливы и для кривых предложения. Для того чтобы измерить коэффициент эластичности в интересующей нас точке на кривой предложения, следует провести касательную к этой точке и определять эластичность полученной касательной.

Задание на самостоятельную подготовку: n изучить парадоксы эластичности