Тема 3 Дифракция света — II Дифракция

Тема 3. Дифракция света - II • Дифракция в параллельных лучах • Дифракция Фраунгофера на круглом отверстии • Дифракция Фраунгофера на щели • Дифракция Фраунгофера на двух щелях • Дифракционная решетка • Дифракция рентгеновских лучей

Дифракция в параллельных лучах (дифракция Фраунгофера) l b Joseph Fraunhofer 1787 -1826 P На дифракционный объект (круглое отверстие, щель и др. ) направляют параллельный пучок света (плоскую волну) и дифракционную картину наблюдают на достаточно большом расстоянии, т. е. практически в параллельных лучах.

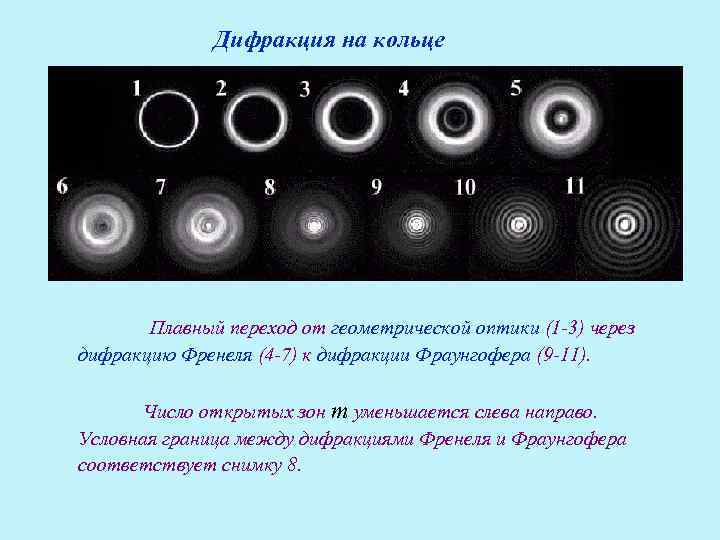Дифракция на кольце Плавный переход от геометрической оптики (1 -3) через дифракцию Френеля (4 -7) к дифракции Фраунгофера (9 -11). Число открытых зон m уменьшается слева направо. Условная граница между дифракциями Френеля и Фраунгофера соответствует снимку 8.

Радиус первой зоны Френеля: l b P Количественный критерий, определяющий тип дифракции: - дифракция Фраунгофера - дифракция Френеля - Геометрическая оптика

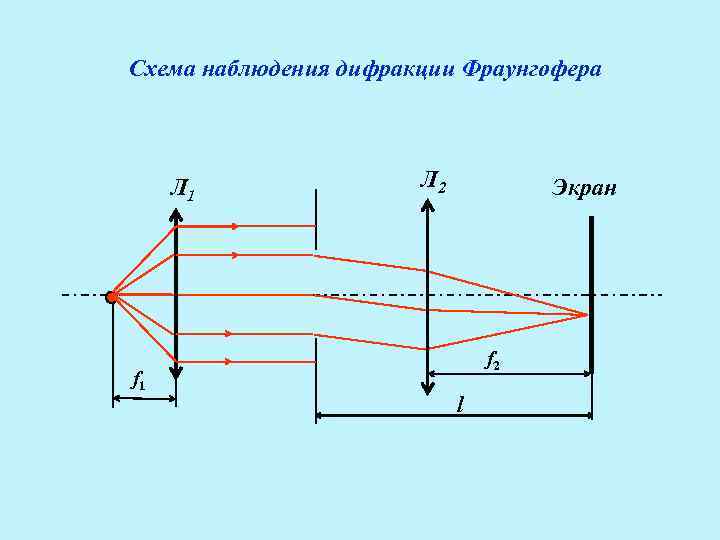Схема наблюдения дифракции Фраунгофера Л 1 f 1 Л 2 Экран f 2 l

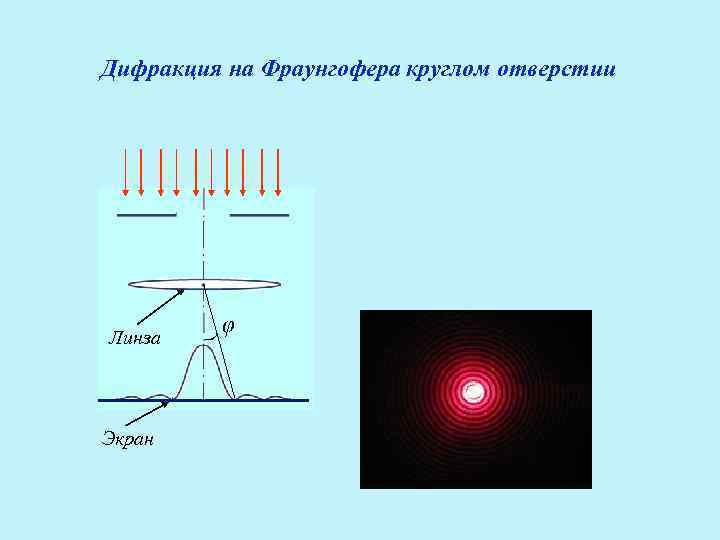Дифракция на Фраунгофера круглом отверстии Экран ) Линза φ

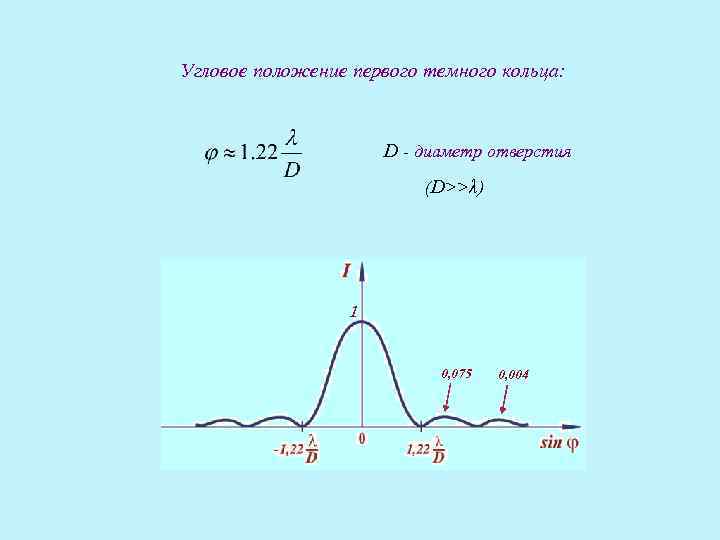Угловое положение первого темного кольца: D - диаметр отверстия (D>>λ) 1 0, 075 0, 004

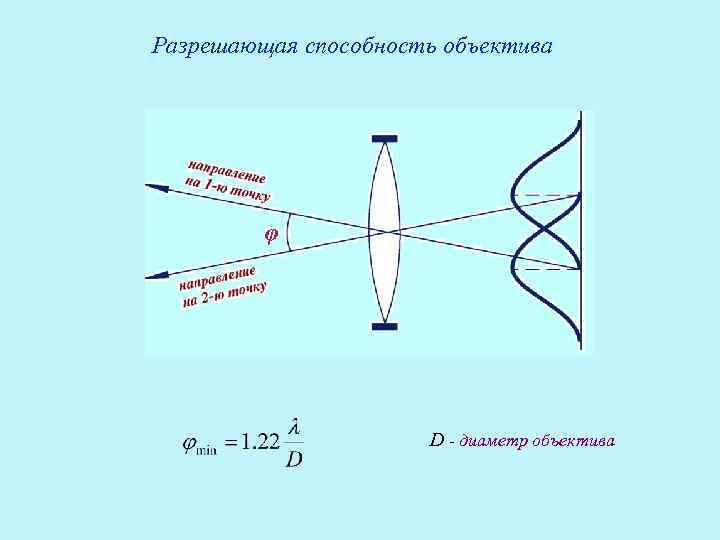Разрешающая способность объектива φ D - диаметр объектива

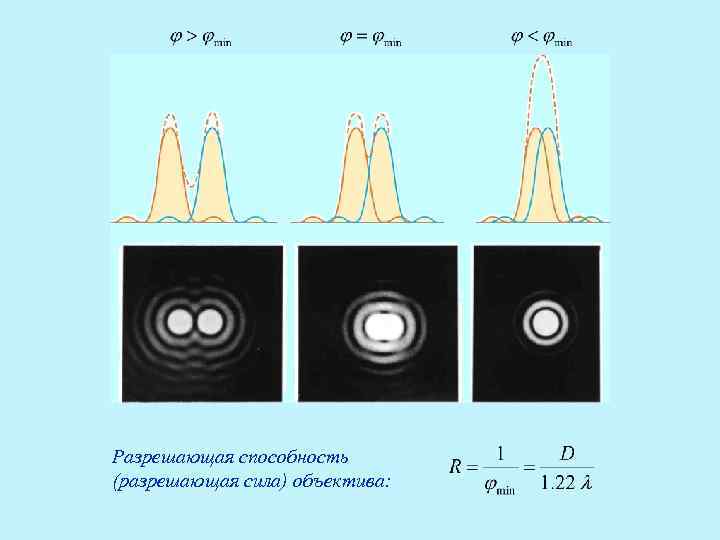Разрешающая способность (разрешающая сила) объектива:

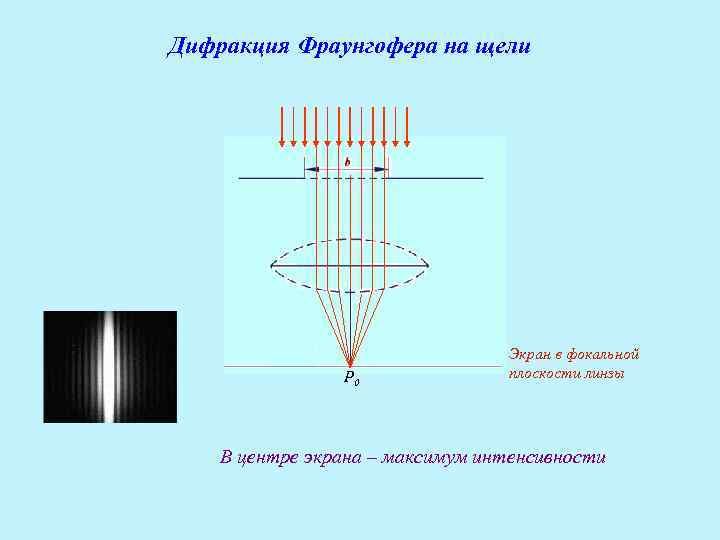Дифракция Фраунгофера на щели P 0 Экран в фокальной плоскости линзы В центре экрана – максимум интенсивности

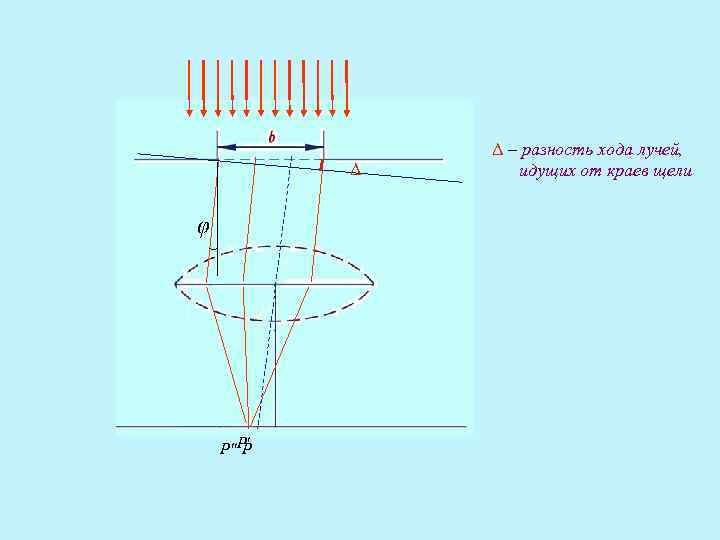Δ Δ ΔΔ φ φ φ P''P' P Δ – разность хода лучей, идущих от краев щели

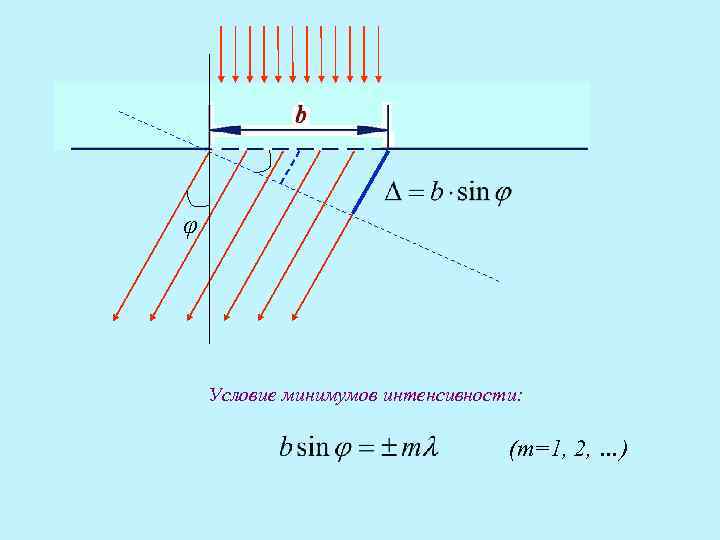φ Условие минимумов интенсивности: (т=1, 2, …)

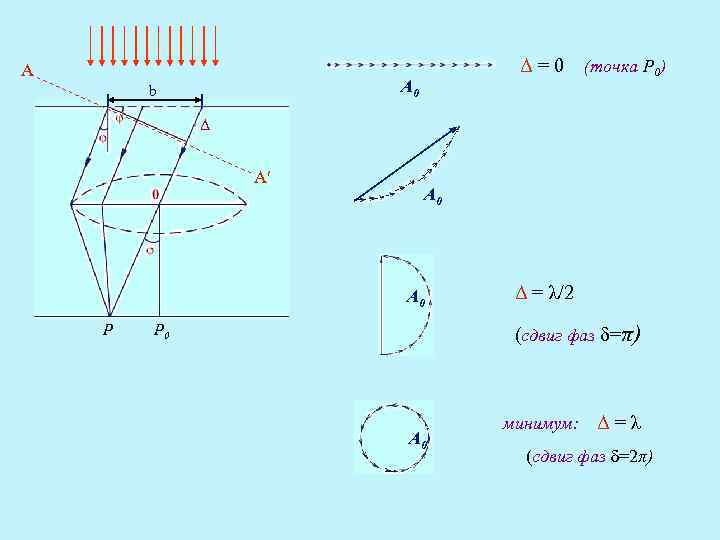Δ=0 А А 0 b (точка Р 0) Δ Аʹ А 0 P Δ = λ/2 (сдвиг фаз δ=π) P 0 А 0 минимум: Δ=λ (сдвиг фаз δ=2π)

максимум: Δ = 3λ/2 А 0 (сдвиг фаз δ=3π) максимум: Δ = 5λ/2 (сдвиг фаз δ=5π) Условие максимумов (кроме центрального): (т=1, 2…)

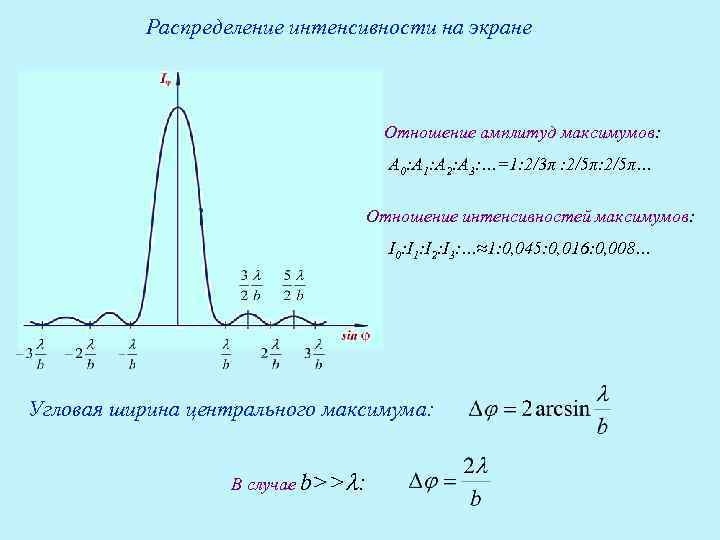Распределение интенсивности на экране Отношение амплитуд максимумов: A 0: A 1: A 2: A 3: …=1: 2/3π : 2/5π… Отношение интенсивностей максимумов: I 0: I 1: I 2: I 3: …≈1: 0, 045: 0, 016: 0, 008… Угловая ширина центрального максимума: В случае b>> :

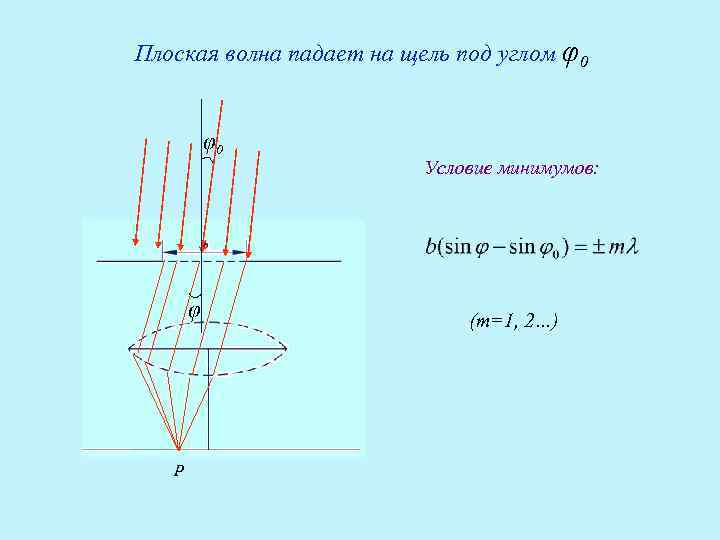Плоская волна падает на щель под углом φ0 φ0 φ P Условие минимумов: (т=1, 2…)

Дифракция Фраунгофера на вертикальной щели по мере ее расширения слева направо. Увеличение ширины щели (b) приводит к сужению дифракционной картины

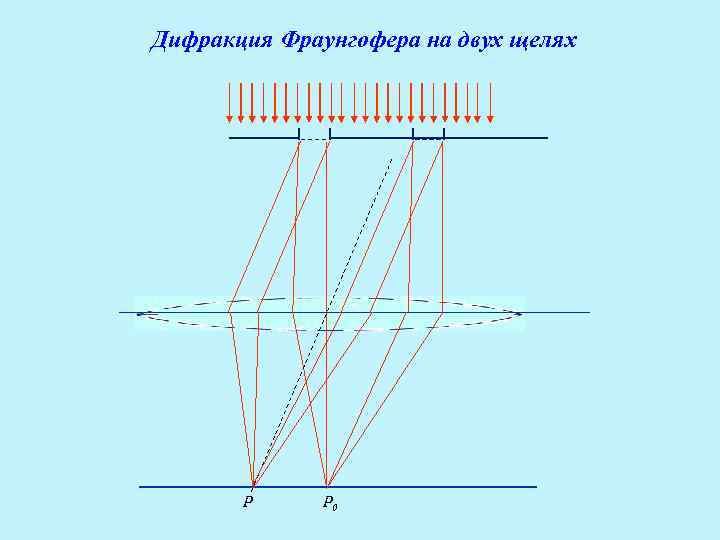Дифракция Фраунгофера на двух щелях P P 0

Условие интерференционного max: Условие интерференционного min: =d sin φ – оптическая разность хода между щелями

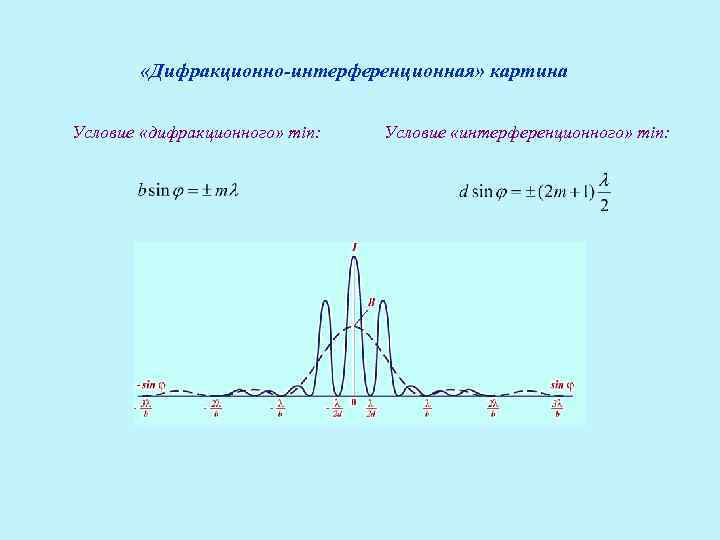«Дифракционно-интерференционная» картина Условие «дифракционного» min: Условие «интерференционного» min:

Ширина щелей b остается постоянной (1 мкм), расстояние d между щелями изменяется в диапазоне 1 -10 мкм. Частота следования интерференционных полос увеличивается пропорционально расстоянию d между щелями, ширина дифракционной картины остаётся неизменной (зависит только от b).

Ширина каждой щели b изменяется, а расстояние между щелями d остается постоянным. При уменьшении b ширина дифракционной картины увеличивается, а ее яркость уменьшается, период интерференционных полос остаётся неизменным.

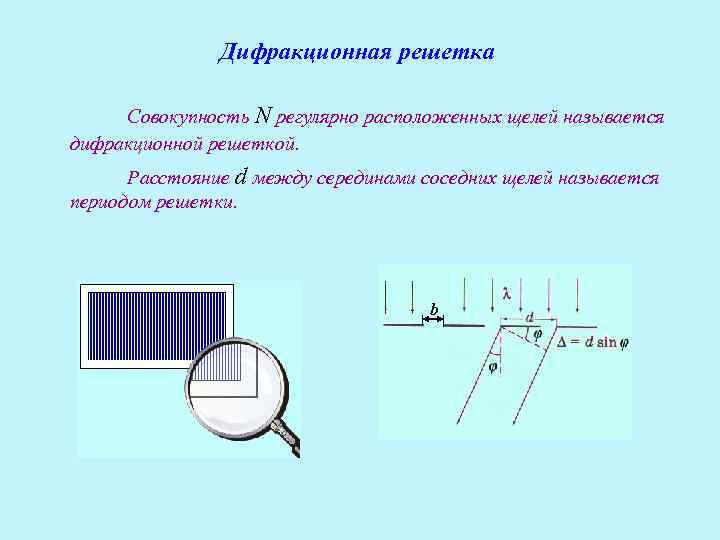Дифракционная решетка Совокупность N регулярно расположенных щелей называется дифракционной решеткой. Расстояние d между серединами соседних щелей называется периодом решетки. b

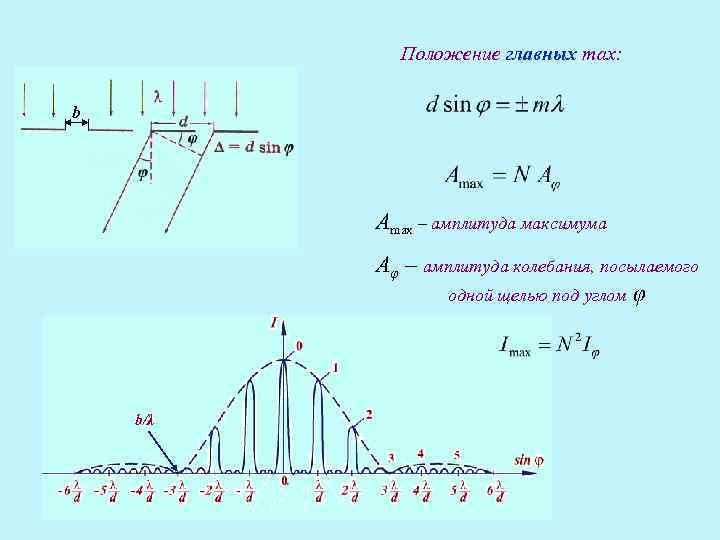Положение главных max: b Amax – амплитуда максимума Aφ – амплитуда колебания, посылаемого одной щелью под углом φ b/λ

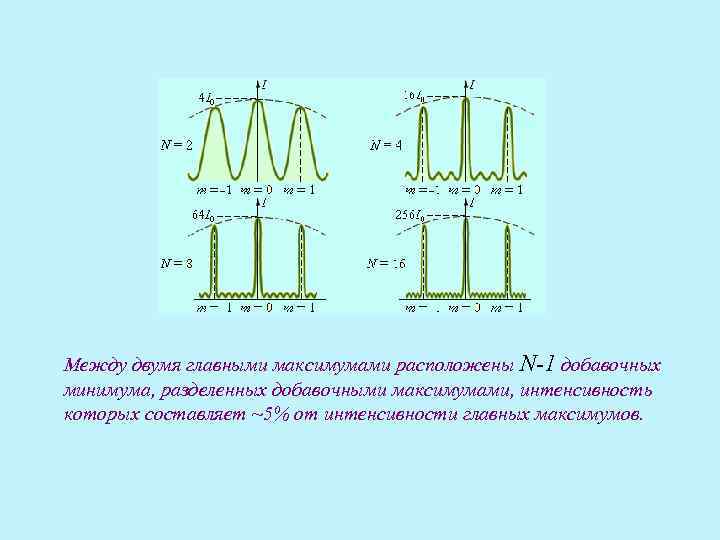Между двумя главными максимумами расположены N-1 добавочных минимума, разделенных добавочными максимумами, интенсивность которых составляет ~5% от интенсивности главных максимумов.

Положение добавочных минимумов: Ширина m-го главного максимума определяется положением двух соседних дополнительных минимумов:

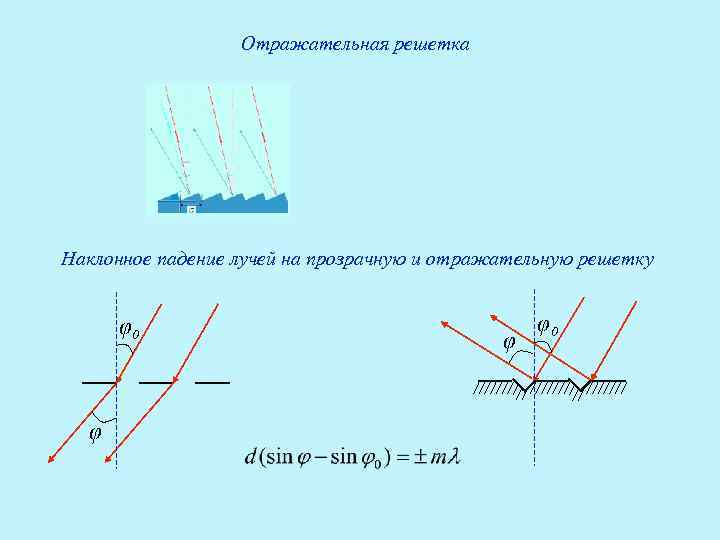Отражательная решетка Наклонное падение лучей на прозрачную и отражательную решетку φ0 φ φ φ0

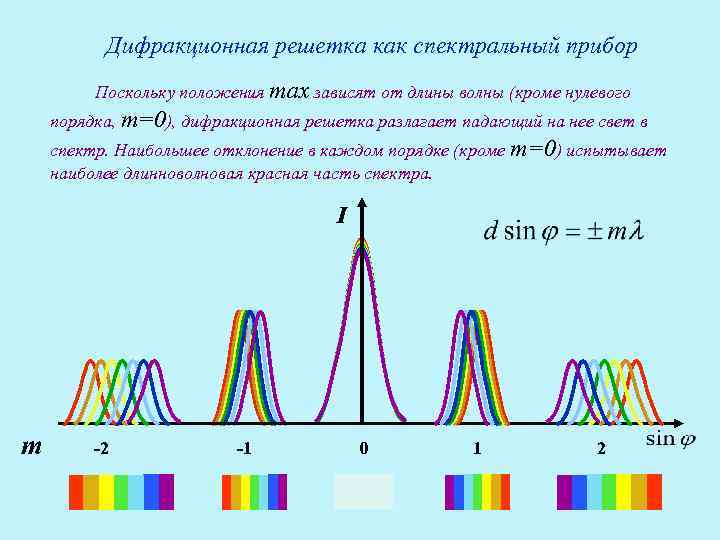Дифракционная решетка как спектральный прибор Поскольку положения max зависят от длины волны (кроме нулевого порядка, т=0), дифракционная решетка разлагает падающий на нее свет в спектр. Наибольшее отклонение в каждом порядке (кроме т=0) испытывает наиболее длинноволновая красная часть спектра. I m -2 -1 0 1 2

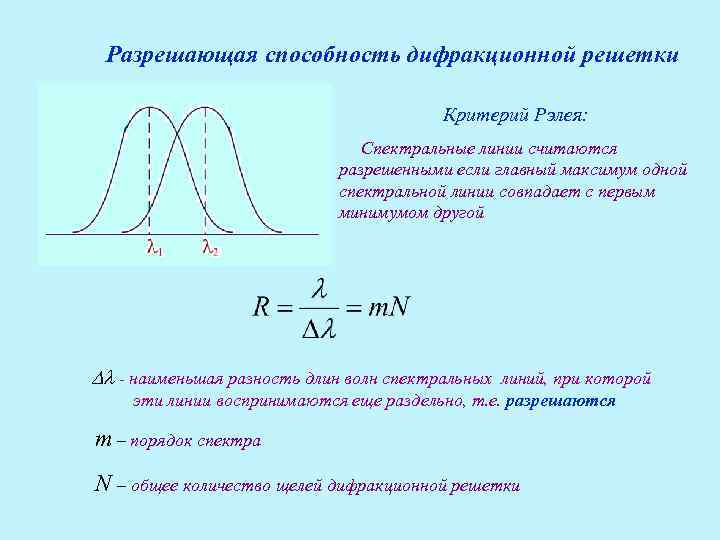Разрешающая способность дифракционной решетки Критерий Рэлея: Спектральные линии считаются разрешенными если главный максимум одной спектральной линии совпадает с первым минимумом другой - наименьшая разность длин волн спектральных линий, при которой эти линии воспринимаются еще раздельно, т. е. разрешаются m – порядок спектра N – общее количество щелей дифракционной решетки

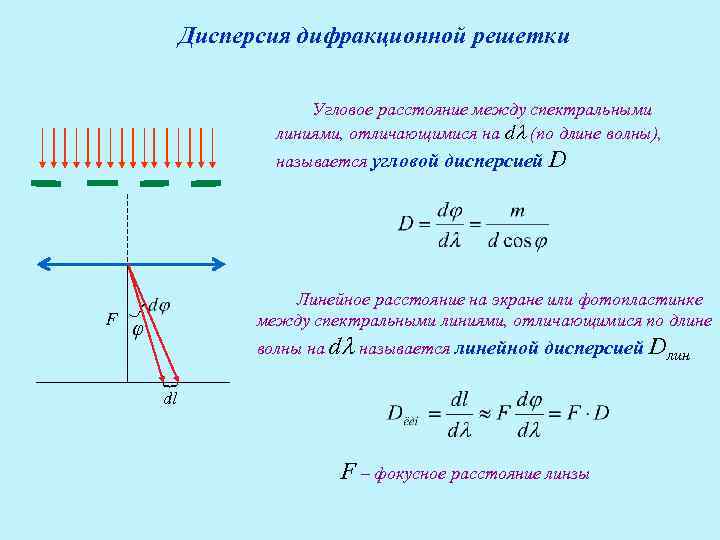Дисперсия дифракционной решетки Угловое расстояние между спектральными линиями, отличающимися на d (по длине волны), называется угловой дисперсией D φ волны на d называется линейной дисперсией Dлин { F Линейное расстояние на экране или фотопластинке между спектральными линиями, отличающимися по длине dl F – фокусное расстояние линзы

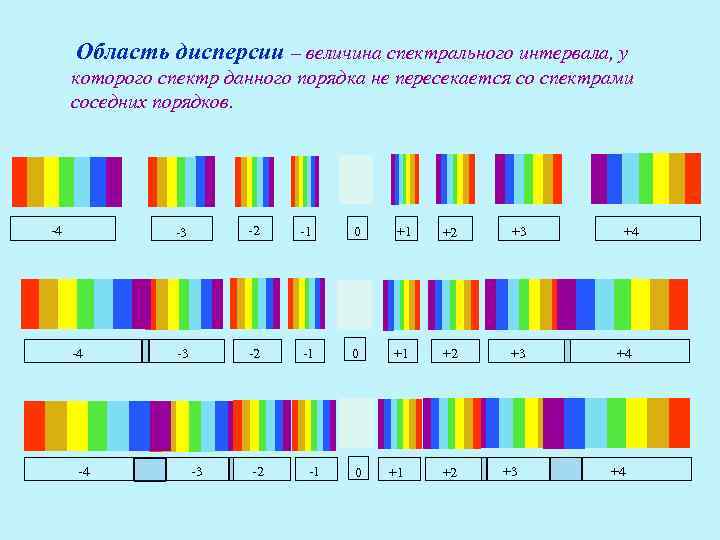Область дисперсии – величина спектрального интервала, у которого спектр данного порядка не пересекается со спектрами соседних порядков. -4 -3 -4 -4 -2 -1 0 +1 +2 +3 -3 -2 -1 0 +1 +2 +3 +4 +4 +4

Дифракция рентгеновских лучей Рентгеновское излучение —электромагнитные волны, расположенные на шкале электромагнитных волн между ультрафиолетовым излучением и гамма-излучением, что соответствует длинам волн от 10− 2 до 103 Å (10− 12 - 10− 7 м).

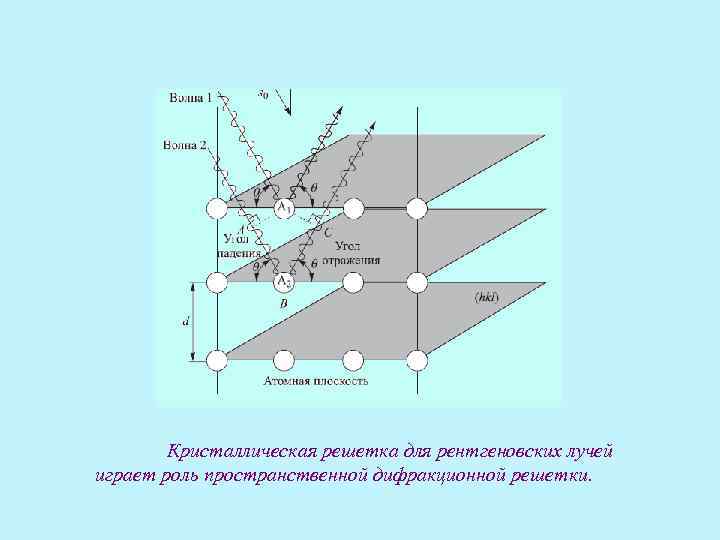Кристаллическая решетка для рентгеновских лучей играет роль пространственной дифракционной решетки.

Углы, на которых наблюдаются дифракционные максимумы, определяются условием Вульфа-Брэгга

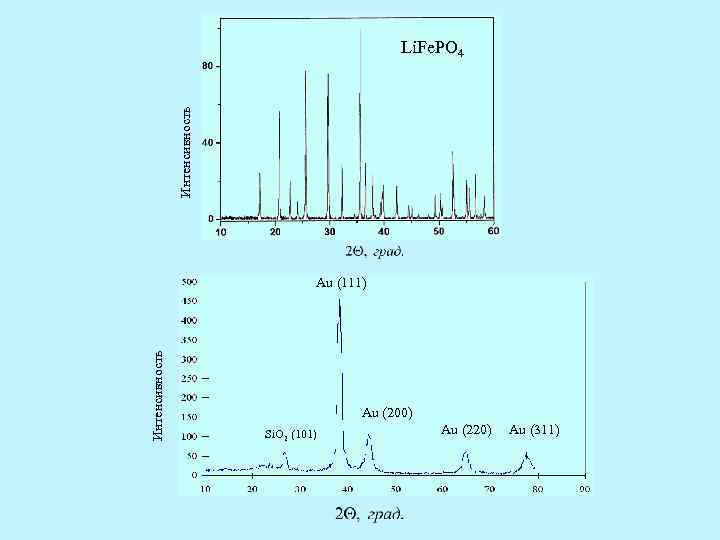Интенсивность Li. Fe. PO 4 Интенсивность Au (111) Au (200) Si. O 2 (101) Au (220) Au (311)

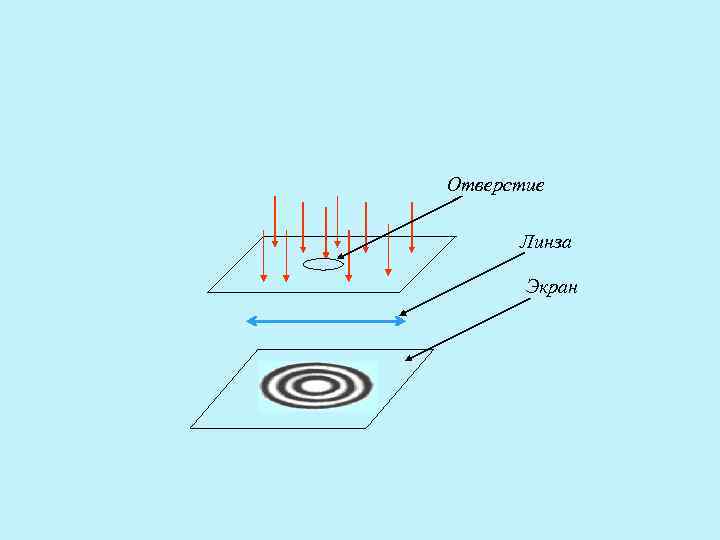Отверстие Линза Экран