Тема 3 1 Типовые звенья типовые воздействия 2

Тема 3 1. Типовые звенья, типовые воздействия. 2. Типовые реакции. Уравнения динамики звеньев. 3. Классификация методов описания линейных элементов. 4. Передаточные функции типовых звеньев

ТИПОВЫЕ ЗВЕНЬЯ Все линейные элементы систем автоматического управления разделяют на классы – “типовые звенья”. Разделение на типы проводят по виду дифференциального уравнения, описывающего динамику элемента, если математическая модель (дифференциальное уравнение) элемента известна. В противном случае тип элемента определяют по виду его реакции y(t) на типовое воздействие x(t), что позволяет восстановить его математическую модель x(t) y(t) элемент ТИПОВОЕ ВОЗДЕЙСТВИЕ – вид входного сигнала, который принято подавать на вход элемента для определения его свойств и параметров (при проведении натурных экспериментов или машинном моделировании). МАТЕМАТИЧЕСКАЯ МОДЕЛЬ - дифференциальное уравнение, показывающее вид связи (зависимости) между координатой состояния y(t) (и всех её производных) и входным воздействием 2 x(t) (и всех её производных).

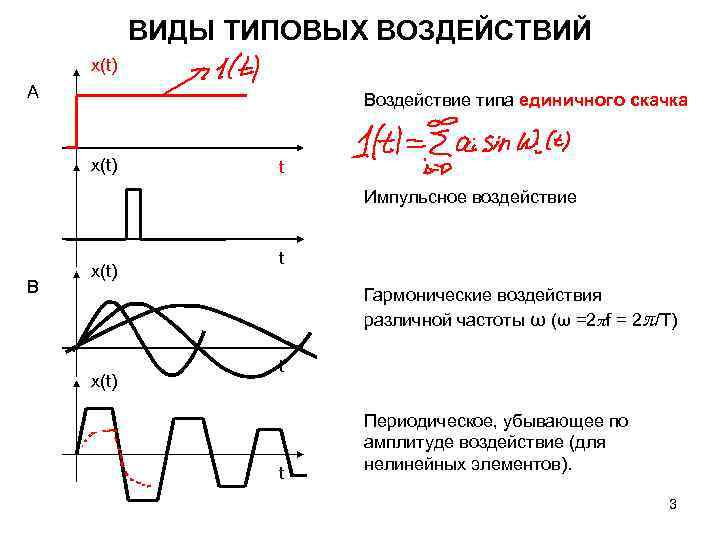ВИДЫ ТИПОВЫХ ВОЗДЕЙСТВИЙ x(t) А Воздействие типа единичного скачка x(t) t Импульсное воздействие B x(t) t Гармонические воздействия различной частоты ω (ω =2πf = 2π/T) x(t) t t Периодическое, убывающее по амплитуде воздействие (для нелинейных элементов). 3

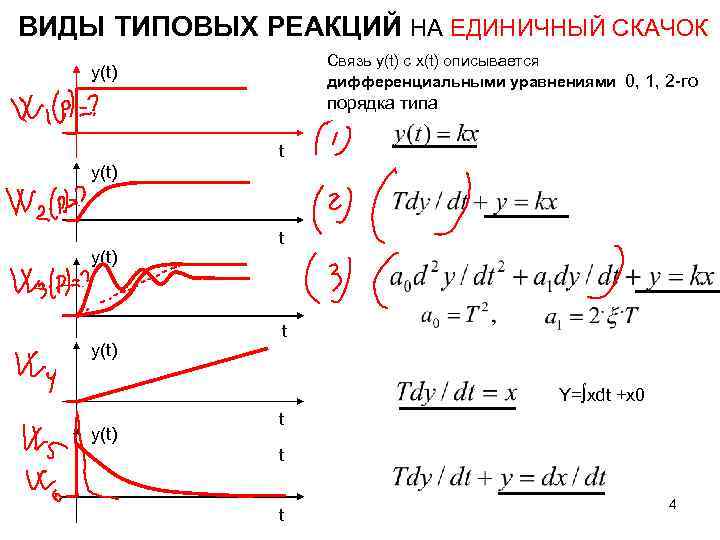ВИДЫ ТИПОВЫХ РЕАКЦИЙ НА ЕДИНИЧНЫЙ СКАЧОК Связь y(t) с x(t) описывается дифференциальными уравнениями 0, 1, 2 -го y(t) порядка типа t y(t) t t Y=∫xdt +x 0 y(t) t t t 4

Итог Между двумя величинами могут существовать три простейшие математические связи (процедуры) – умножение, дифференцирование, интегрирование, осуществляемые типовым звеном. (существуют нелинейные звенья со специфическим назначением, например, звено чистого запаздывания) Y=Kx → усиление (безинерционные, инер ционные, колебательные звенья) Y=dx/dt → дифференцирование Y=∫xdt +x 0 → dy/dt=x → интергрирование x y Звено/элемент В уравнении 3 величины y, F. x Какие можно поставить задачи? Y = ? X F 1. ? 2. ? 3. ? 5

Математическое описание динамики элемента: присутствует время Дифференциальные уравнение для получения уравнения используют законы природы /физики Дифференциальное уравнение наиболее общий инструмент описания элементов или системы связанных физических элементов, образующих техническое устройство или объект. Это устройство/система способна воспринимать внешнее воздействие x(t) и характеризуется некоторой выходной величиной y(t), известным образом зависящей от воздействия x(t). Все остальные методы описания систем прямо или косвенно вытекают из дифференциального уравнения или опираются на него. 6

x(t) – подача энергии U*I=P Тепловой y(t) = Q(t) объект - температура (контролируемый параметр) λ – коэффициент теплоотдачи, а – характеризует способность переводить потребляемую энергию в тепло 8

Для однозначного решения уравнения должны быть заданы начальные условия: (уравнение второго порядка – два начальных условия) значение величины y(0) и её производной y’(0) в начальный, принятый за начало отчета, момент времени. В физической системе эти значения определяются энергией, содержащейся на этот момент времени в элементах, способных ее накапливать, например, в электрических емкостях и индуктивностях, пружинах, подвижных массивных деталях (массах) и т. п. Кроме того, должно быть задано и входное воздействие x(t). Входным воздействием может быть произвольный сигнал, в том числе, например, типовой: ступенчатая единичная функция x(t) = 1(t) или синусоидальный сигнал x(t) = sin(ωt + φ), или более сложные сигналы, изменение которых во времени заранее не известно. Коэффициенты в уравнении (различные комбинации параметров К, Т) считаются известными и определяются конструкцией элемента / системы. 9

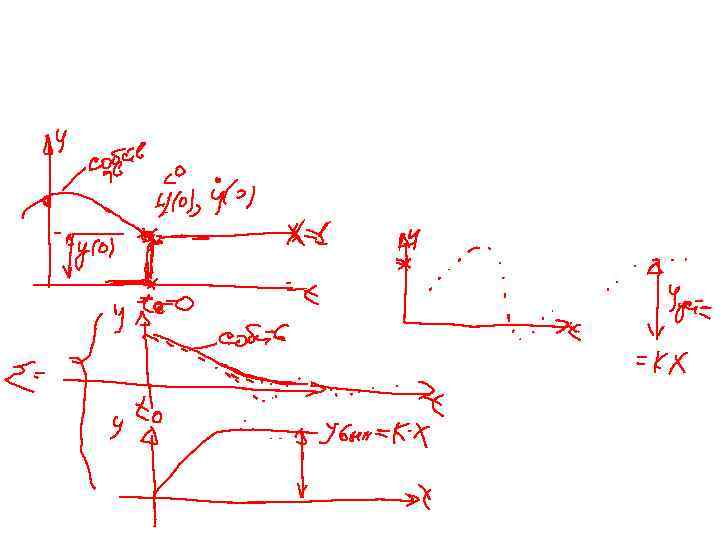
Дифференциальное уравнение при полностью известном воздействии позволяет корректно определить вид переходного и установившегося режима. Эти понятия применяются для устойчивых систем: - переходный режим – это сумма (принцип суперпозиции – сложение реакций работает только для линейных систем) свободной / собственной и вынужденной компонент решения дифференциального уравнения в пределах временного интервала, пока свободная компонента не затухнет. Практический критерий затухания – уменьшение величины амплитуды свободной компоненты в 20 раз по сравнению с максимальным ее значением. Собственная составляющая обусловлена наличием начальных условий и находится из решения диф. уравнения при нулевой правой части. Вынужденная компонента находится при наличии вынуждающего воздействия (ненулевой правой части) и нулевых начальных условиях y “ неудавшийся, невозникший ” переходный режим Вынужденная и собственная компоненты t 10

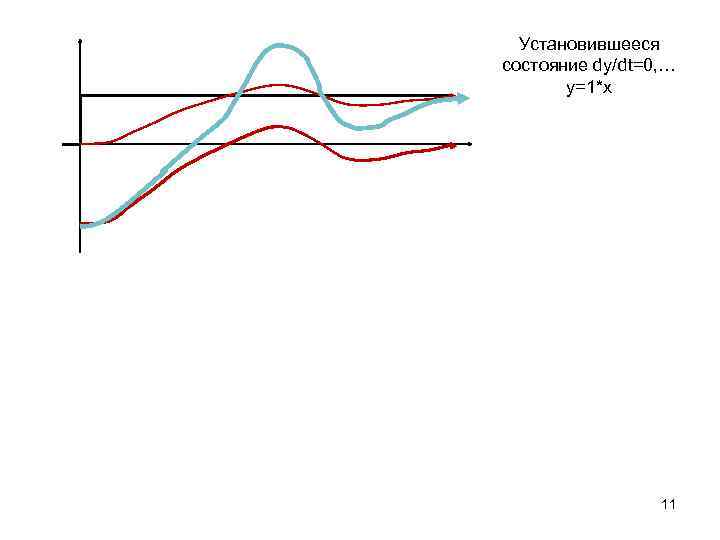Установившееся состояние dy/dt=0, … y=1*x 11

В случае известного заранее воздействия x(t), решение можно получить аналитически. Его удобно представлять в виде суммы вынужденной yв (t) и свободной yсв(t) (правая часть диф. уравнения =0) составляющих т. к. их легко разделить и найти по отдельности. В устойчивых системах yсв(t) затухает с течением времени, поэтому при относительно больших значениях t, при условии, что воздействие достаточно гладкое (т. е. оно и его младшие производные не содержат скачков /разрывов первого рода), выходной сигнал системы приближается к вынужденному. . 12

Свободная компонента в решении уравнения определяется корнями pk характеристического полинома A(p) исходного уравнения (1): где Т – период собственных колебаний 13

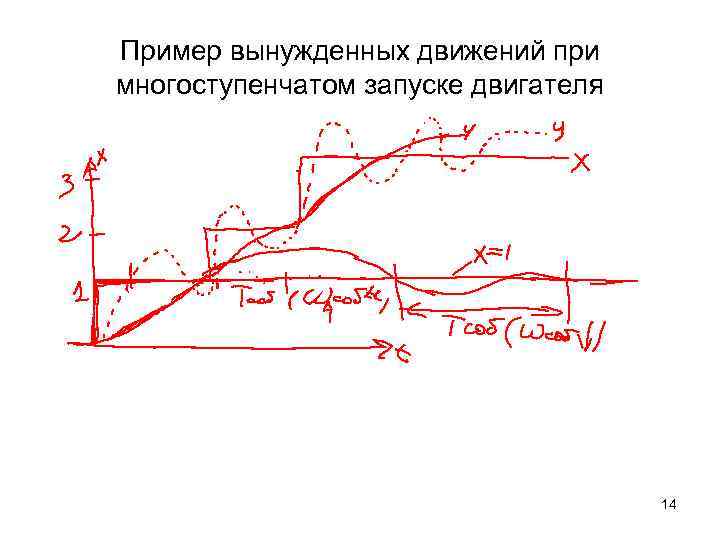Пример вынужденных движений при многоступенчатом запуске двигателя 14

aпостериорные методы (по результатам эксперимента) При реализации этих методов воздействие вначале преобразуется в изображение (операторный метод) или спектр (спектральный метод), затем определяется изображение или спектр реакции и, после чего восстанавливается временная реакция на воздействие (что находится обратным преобразованием – спектр или изображение переводится во временную функцию) или определяется передаточная или комплексно-передаточная фукция системы, . Такой «обходной» путь во многих случаях упрощает решение задач. 15

Преобразование Лапласа — интегральное преобразование, связывающее функцию комплексного переменного (изображение - F(p)) с функцией действительного переменного (оригинал - f(t)). . Преобразование Фурье 16

Операторный метод Довольно часто можно встретить заблуждение, состоящее в том, что понятия комплексный коэффициент передачи (ККП) – W ( jω ) и передаточная функция W(p) - это пр актически одно и то же, они отличаются только обозначением аргументов и поэтому области их применения одинаковы. Это происходит потому, что обычно автоматчики рассматривают линеаризованные модели САР с приращениями воздействий и реакций относительно некоторого стационарного режима. Такая модель предполагает, что начальные условия для приращений являются нулевыми. На самом деле, ККП и передаточная функция отличаются и по смыслу, и по кругу решаемых ими задач. Если ККП это первый уровень обобщения понятия коэффициент усиления, когда учитываются зависимость величины усиления устройства от частоты усиливаемого им синусоидального сигнала, а также зависимость фазовой задержки от частоты сигнала, проходящего систему, то передаточная функция это следующий, второй уровень обобщения. 17

При ненулевых начальных условиях 18

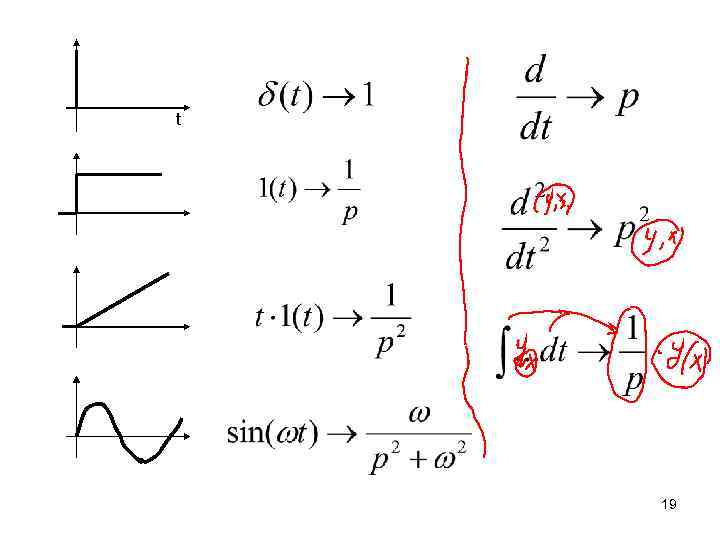t 19

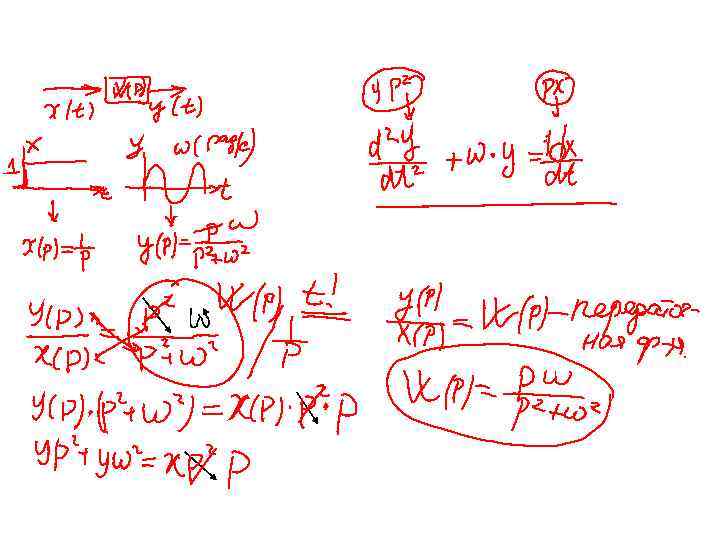
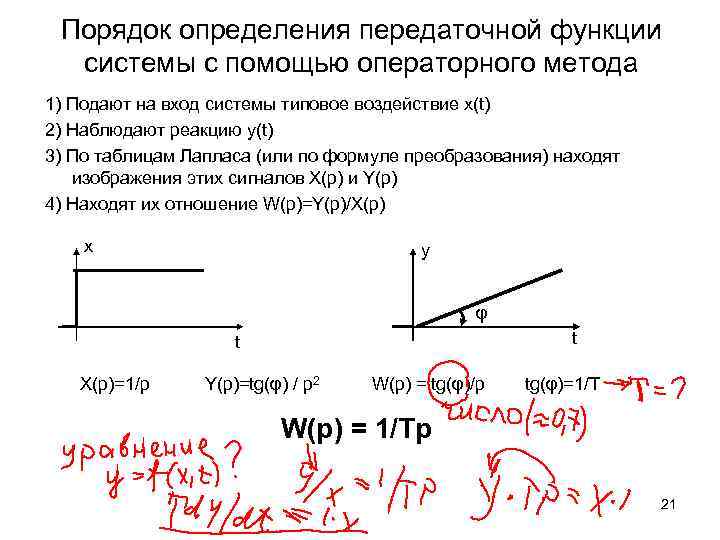Порядок определения передаточной функции системы с помощью операторного метода 1) Подают на вход системы типовое воздействие x(t) 2) Наблюдают реакцию y(t) 3) По таблицам Лапласа (или по формуле преобразования) находят изображения этих сигналов X(p) и Y(p) 4) Находят их отношение W(p)=Y(p)/X(p) x y φ t t X(p)=1/p Y(p)=tg(φ) / p 2 W(p) = tg(φ)/p tg(φ)=1/T W(p) = 1/Tp 21

Передаточная функция может все то, что может комплексный коэффициент усиления, но в добавок она позволяет учитывать и начальные условия системы, а следовательно, описывать и рассчитывать переходное процессы Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соотвествуют более простые соотношения над их изображениями 22

Спектральный метод основан на оценке спектрального состава входного и выходного сигнала или записи вида входного и выходного сигнала после преобразования его с помощью интеграла Фурье. Пример 23

Комплексное число можно разложить на действительную и мнимую составляющую и построить Комплексный Коэффициент Передачи на плоскости Re – Im. R – модуль W(jω), а φ – фаза W(j ω) (фаза, на которую задерживается сигнал, проходя через устройство). Таким образом, зная эти величина и характеристики входного сигнала, можно определить характеристики выходного сигнала. Im φ Im(ω1) Re(ω1) R ω Re 2ω 3ω Амплитудно-фазочастотная характеристики устройства 24

Функции частоты |W(ω)| и φ(ω) - называются амплитудно- и фазочастотной характеристиками системы. В проведенных рассуждениях и выкладках нигде не использовались начальные условия (НУ) дифференциального уравнения, они предполагаются нулевыми (или другими) в минус бесконечности, когда синусоида включилась, возникла. Тогда же закончился и переходный процесс, вызванный ее подачей на систему. Т. о. решение задачи с помощью комплексного коэффициента передачи ККП показывает, что линейное звено в широком диапазоне времен задерживает синусоиду по фазе и изменяет ее амплитуду, переходного процесса здесь нет, а существует только установившийся режим. Эти задержка по фазе и изменение амплитуды зависят от частоты входного синусоидального сигнала. 25

Если сигнал сложный, то его можно аппроксимировать суммой синусоид. Для линейной системы справедлив принцип суперпозиции, поэтому при воздействие на нее сложного сигнала, состоящего из совокупности синусоид, реакция может быть найдена суммированием реакций на отдельные синусоиды. 26

Выводы Дифференциальное уравнение – универсальный математический инструмент. Оно позволяет описывать линейную систему текущем времени, , а также учитывать начальные условия. Для известного входного сигнала и начальных условиях, дифференциальное уравнение позволяет найти отдельно свободную и вынужденную составляющие решения, определить переходной и установившийся режимы работы САР. Дифференциальное уравнение быстро и эффективно решается численно, моделирующие программы предоставляют многочисленные методы его решения. . 27

Операторный метод используют при отсутствии математического описания (в виде диф. уравнения) объекта, но возможности проведения опыта натурного эксперимента. Находя соотношение выходного и входного сигнала, записанных в операторном виде, находят передаточную функцию → характеристическое уравнение → корни характеристичекого уравнения → динамику собственных движений → общую динамику (собственные + вынужденные движения, если известно математическое описание вынужденных воздействий). Операторный метод учитывает начальные условия и работает с сигналами, начинающимися в нулевой момент. В операторном методе, как и в методе дифференциального уравнения может оказаться так, что переходный процесс в момент подачи воздействия на систему не возникает, т. к. начальные условия уже обеспечили то состояние, к которому должна привести вынуждающая сила. Спектральный метод (так же как и операторный, при возможости проведения опыта) рассматривает сигналы, начинающиеся в минус бесконечности и заканчивающиеся в плюс бесконечности, и не учитывает начальные условия, точнее считает их произвольными, но отнесенными к бесконечному времени в прошлом. Передаточная функция W(p) отличается от комплексного коэффициента передачи 28 W(jω) только обозначением аргумента: p = jω.

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ТИПОВЫХ ЗВЕНЬЕВ Передаточная функция { W(p) } показывает связь/зависимость между входным и выходным сигналом { причиной и следствием }, но не во временном пространстве, а в некотором новом пространстве p, предложенным Лапласом. Переход от пространства t в пространство p осуществляется с помощью формулы Таким образом (при нулевых начальных условиях) или В новом пространстве все математические процедуры меняют свой вид (кроме процедуры умножения переменной величины на константу). 29

Если есть возможность провести натурный эксперимент, то можно подать на вход элемента типовое воздействие, например, единичный скачок, и зафиксировать его реакцию – переходный процесс (при нулевых начальных условиях). Лаплас в своих таблицах множеству сигналов, представленных в графической форме и временном пространстве, дал математическое описание в виде функции от параметра P. x x(t) ? y(t) t y t x(p) W(p) y(p) В этом случае передаточная функция находится как отношение y(p) / x(p) 30

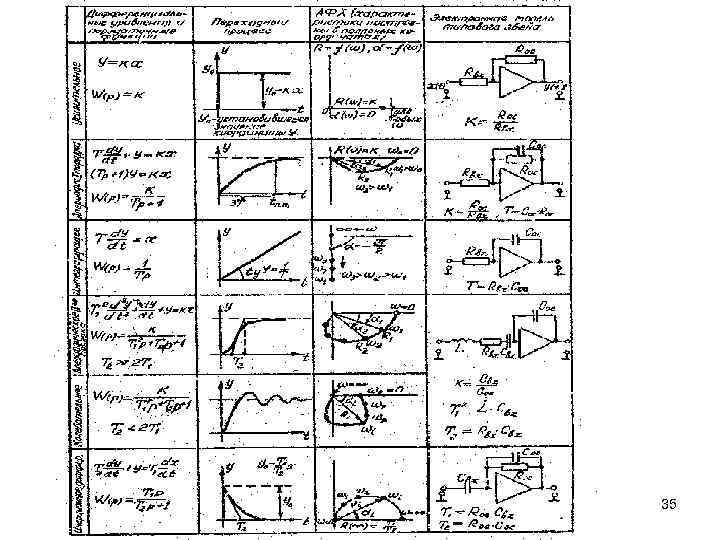
Усилительное безинерционное звено Инерционное звено первого порядка Колебательное и инерционное звено второго порядка Интегрирующее звено Инерционное дифференцирующее звено 31

Коэффициенты уравнений К , Т , … - собственные параметры элементы, определяемые его конструкцией. К - коэффициент передачи/усиления внешнего (постоянного по величине) воздействия. Т- постоянная времени, характеризует инерцию элемента, влияет на длительность переходных процессов. ξ - коэффициент затухания. От уравнений динамики элементов легко перейти к уравнениям статики, приравняв нулю все производные. В усилительных (инерционных и безинерционных) звеньях уравнения статики имеет вид В дифференцирующем В интегрирующем звене уравнение статики отсутствует. 32

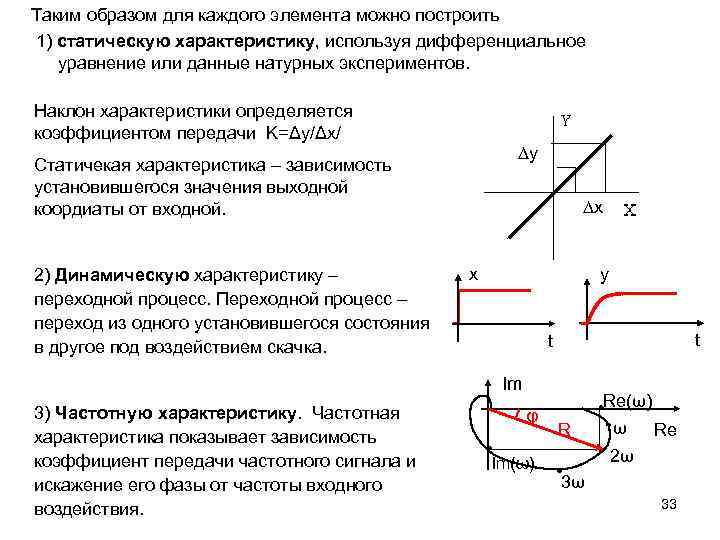Таким образом для каждого элемента можно построить 1) статическую характеристику, используя дифференциальное уравнение или данные натурных экспериментов. Наклон характеристики определяется коэффициентом передачи K=Δy/Δx/ ∆y Статичекая характеристика – зависимость установившегося значения выходной коордиаты от входной. 2) Динамическую характеристику – переходной процесс. Переходной процесс – переход из одного установившегося состояния в другое под воздействием скачка. ∆x x y t t Im 3) Частотную характеристику. Частотная характеристика показывает зависимость коэффициент передачи частотного сигнала и искажение его фазы от частоты входного воздействия. φ Im(ω) Re(ω) R ω Re 2ω 3ω 33

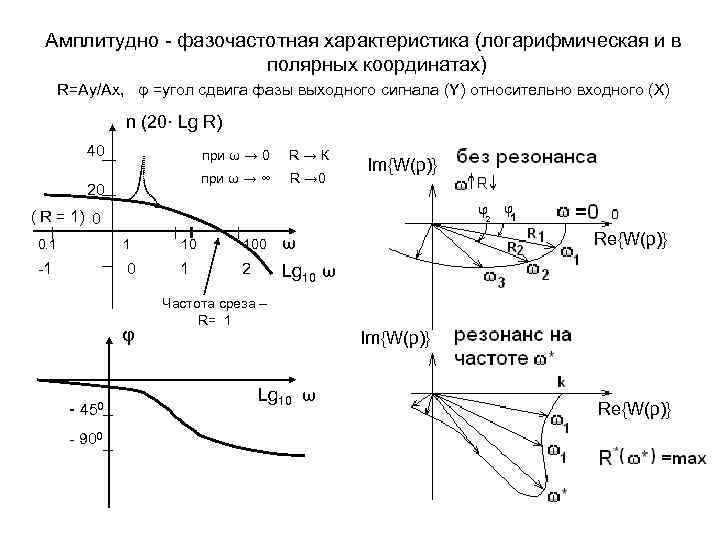Амплитудно - фазочастотная характеристика (логарифмическая и в полярных координатах) R=Ay/Ax, φ =угол сдвига фазы выходного сигнала (Y) относительно входного (X) n (20· Lg R) 40 20 при ω → 0 R → К при ω → ∞ R → 0 Im{W(p)} ( R = 1) 0 0. 1 10 100 -1 0 1 2 φ - 450 Re{W(p)} ω Lg 10 ω Частота среза – R= 1 Lg 10 ω Im{W(p)} Re{W(p)} - 900 34

35

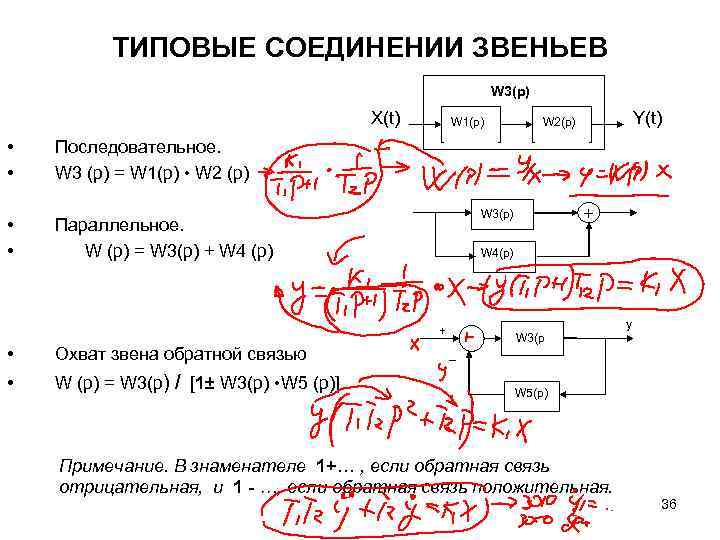ТИПОВЫЕ СОЕДИНЕНИИ ЗВЕНЬЕВ W 3(p) X(t) • • Параллельное. W (p) = W 3(p) + W 4 (p) Y(t) W 2(p) Последовательное. W 3 (p) = W 1(p) • W 2 (p) • • W 1(p) • Охват звена обратной связью • W (p) = W 3(p) / [1± W 3(p) • W 5 (p)] + W 3(p) W 4(p) + – y W 3(p W 5(p) Примечание. В знаменателе 1+… , если обратная связь отрицательная, и 1 - …, если обратная связь положительная. 36

ИТОГ • У каждого элемента/узла проверяется динамика (переходный процесс и частотная характеристика) и статика (статическая характеристика). • Способы оценки динамики: по дифференциальному уравнению, по передаточной функции, по комплексному коэффициенту передачи. • Любой из способов позволяет вывести характеристическое уравнение, найти корни и оценить вид собственных движений элемента (системы). • Зная вид воздействия, можно предсказать реакцию, как сумму собственных и вынужденных движений. 37

Лаплас (Laplace) Пьер Симон (1749– 1827, Париж), французский астроном, математик и физик, член Парижской АН (1785, член Французской академии (1816). Учился в школе бенедиктинцев, из которой вышел, однако, убеждённым атеистом. В 1766 Лаплас приехал в Париж, где Ж. д’Аламбер через пять лет помог ему получить место профессора Военной школы. Деятельно участвовал в реорганизации системы высшего образования во Франции, в создании Нормальной и Политехнической школ. Научное наследие Лапласа относится к области небесной механики, математики и математической физики, фундаментальными являются работы по дифференциальным уравнениям Лаплас Пьер Симон 23 марта 1749 года - 5 марта 1827 года 38

История жизни Наполеон, который очень верно судил о людях, так писал на острове Святой Елены о Лапласе в своих воспоминаниях «Великий астроном грешил тем, что рассматривал жизнь с точки зрения бесконечно малых» . Действительно, все, что не касалось науки, было для Лапласа бесконечно малым. Строгий и взыскательный к себе, когда дело шло о науке, в обыденной жизни Лаплас поступал иногда хорошо, иногда плохо, смотря по обстоятельствам, пренебрегая всем этим, как бесконечно малым, во имя главного дела своей жизни — научного творчества. Ради науки он даже менял свои убеждения. Видимо, стоит отнестись к некоторым моментам в жизни Лапласа, как к бесконечно малому в сравнении с тем великим и значительным, что создал ученый в астрономии, математике и физике. Пьер Симон Лаплас родился 23 марта 1749 года в местечке Бомонан -Ож (Нормандия) в семье небогатого крестьянина. Впоследствии граф и маркиз Лаплас стыдился своего незнатного происхождения, поэтому о его детских и юношеских годах известно очень немногое. Пьер Симон рано проявил свои выдающиеся способности, с блеском окончил школу бенедиктинцев, и был оставлен там же, в Бомоне, преподавателем математики военной школы. В семнадцать лет написал свою первую научную работу. Жизнь в захолустном Бомоне тяготила Лапласа и в 1766 году он отправился в Париж. Там с помощью д`Аламбера он получил место преподавателя математики в Военной школе Парижа. И т. д. …. 39

Преобразова ние Лапла са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) F(p) с функцией вещественного переменного (оригинал) F(t). . С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения 40

41

ФУРЬЕ Жан Батист Жозеф(21. 3. 1768 -16. 5. 1830) Фурье родился 21 марта 1768 г. в семье бедного портного в г. Осере. На девятом году жизни он потерял обоих родителей. Сироту устроили в Военную школу, руководимую монахами Бенедиктинского ордена. Особый интерес и необыкновенные способности мальчик проявлял в области математики, и его мечтой было стать военным инженером. Лежандр, бывший инспектором школ, пытался помочь в этом одаренному юноше, но министр отказался зачислить его в военноартиллерийское училище: у Фурье не было ни дворянской грамоты, ни денежных средств. Оставалась карьера служителя церкви, быть может, в должности преподавателя. Революция открыла перед Фурье другой путь. В 1789 г. он приехал в Париж и представил Академии наук работу о численном решении уравнений любой степени, которая однако, потерялась в вихре тогдашних событий. Фурье вернулся в Осер и начал преподавать в той школе, где ранее учился. 42

В это время он становиться завидным политическим деятелем. Фурье занял весьма умеренную позицию по отношению к якобинцам и за это был арестован. Падение Робеспьера в июле 1794 г. освободило его от тюрьмы. Он поступает в Нормальную школу, организованную в то время Конвентом с целью подготовки учителей. Нормальная школа просуществовала недолго, но Фурье уже успел обратить на себя внимание Монжа, Лагранжа, Лапласа Когда в 1795 г. для подготовки инженеров, прежде всего военных, была основана Политехническая школа, Фурье пригласил работать в ней в качестве помощника Лагранжа, и Монжа. Он вел занятия по всему циклу математических наук. Основным объектом исследования Фурье была математическая физика. В 1807 -1811 гг. он систематически подавал в Парижской Академии Наук свои открытия по теории теплопроводности в твердом теле. Результаты его исследований были опубликованы в 1822 г. в монографии "Аналитическая теория тепла"; главным в них были выводы уравнения теплопроводности и разработка методов его интегрирования при различных граничных условиях, например метода (метод Фурье) разделения переменных, в основе которого лежит представление функций тригонометрическими рядами (рядами Фурье). 43

Такие ряды применялись и раньше, но только у Фурье они стали настоящим орудием математической физики. Фурье нашел формулу представления функции с помощью интеграла, играющую важную роль в современной математике. "Аналитическая теория тепла" Фурье и примененные в ней методы стали основой для создания теории тригонометрических рядов и разработки некоторых других общих проблем математического анализа. Фурье доказал, что всякую произвольно начерченную линию, составленную из отрезков дуг разных кривых, можно представить единым аналитическим выражением. Хотя Фурье и не доказал, что любую функцию можно разложить в тригонометрический ряд, но его попытки осуществить такое разложение были толчком к ряду исследованию по этой проблеме. 44

МЕТОДЫ ОПИСАНИЯ ЛИНЕЙНЫХ ЭЛЕМЕНТОВ Методы текущего времени дифференциальные уравнения Апостериорные мтоды (a posteriori – знание пришедшее из опыта, a priori – до опыта), методы, описывающие реакцию элемента по результатам опыта Спектральный метод ( используются комплексные коэффициенты передачи - W(jω)). Операторный метод (метод преобразования Лапласа или метод передаточной функции W(p) ). Статистический метод. 45