Тема 2. Случайные величины Х P … p 1 p 2 … pn
ТЕМА 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
.
Пример 2. Монету подбрасывают 3 раза. С. в. X – число выпавших гербов. Найти распределение Х. {Выпадения Г} – У, р=0, 5; Х- число успехов в 3 -х исп-х Б. с вер. У р=0, 5; P{X=0} =Р 3(0) =С 30 р0 q 3 =1/8; P{X=1} =Р 3(1) =С 31 р q 2 =3/8; P{X=2} =Р 3(2) =С 32 р2 q 1 =3/8; P{X=3} =Р 3(3) =p 3 =1/8; хi 0 1 2 3 pi 1/8 3/8 1/8
§ 3. Функция от д. с. в. • Х -2 -1 0 1 2 р 0, 1 0, 2 0, 3 0, 1 У 0 1 4 р 0, 3 0, 5 0, 2
§ 4. Независимость двух д. с. в. •
§ 5. Математическое ожидание (среднее значение) д. с. в. Х х1 х2 … хn P Пусть Х им. расп-е p 1 p 2 … pn Опр 1. Математическим ожиданием д. с. в. Х наз. число Усл. Пр. 2. § 2 Опр 2. Если с. в. Х им. счетное множ-во значений, то говорят, что м. о. сущ-т и равно , если ряд сходится.
Пример Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем в 500 руб. , 10 билетов с выигрышем в 100 руб. и остальные 89 билетов – без выигрышей. Наудачу выбирается 1 билет. Найти мат. ожидание выигрыша.
§ 6. Свойства математического ожидания 1. 2. 3. Е(с)=с. Е(с. Х)= с Е(Х). Свойство аддитивности. Для любых двух с. в. Х и У Е(Х+У)=Е(Х)+Е(У). Док-во.
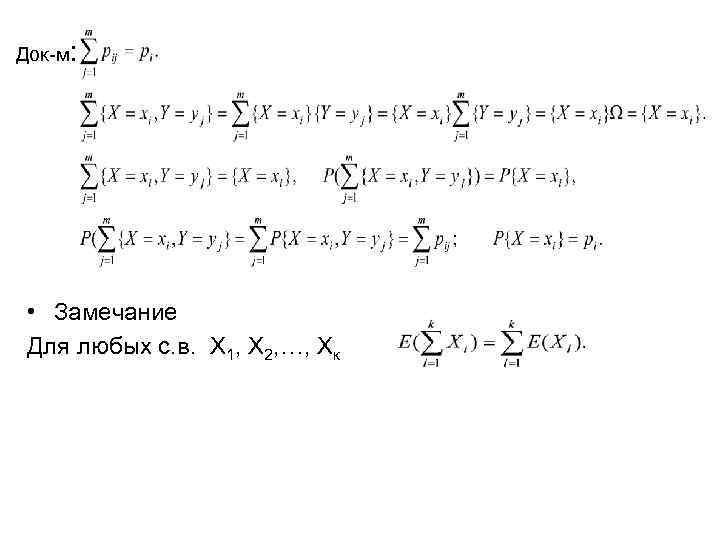Док-м: • Замечание Для любых с. в. Х 1, Х 2, …, Хк
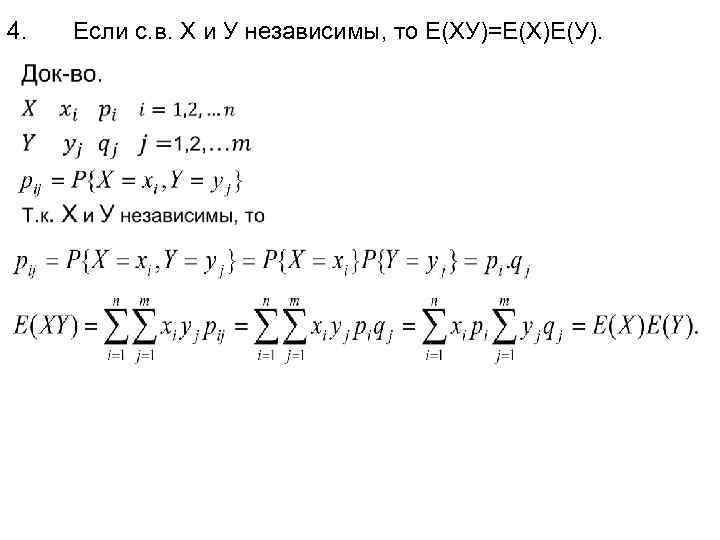4. • Если с. в. Х и У независимы, то Е(ХУ)=Е(Х)Е(У).
Пр. 1. Х и У-независимы и заданы их распределения а. Найти Е(Х У). Х -1 0 3 Y 1 4 p 0, 4 0, 5 0, 1 p 0, 7 0, 3 Е(Х У)=Е(Х)Е(У). Е(Х)=-0, 4+0, 3= -0, 1; Е(У)=0, 7+1, 2=1, 9; Е(Х У) =-0, 1*1, 9=- 0, 19; б. Е(2 Х-3 У+1)=?
ДОМ. ЗАДАНИЕ 1. Производятся 2 выстрела с вероятностями попадания в цель равными 0, 4 и 0, 3. Найти м. о. общего числа попаданий в цель. 2. Вероятность сдачи экзамена первым студентом равна 0, 6, а вторым – 0, 9. Составить таблицу распределения с. в. Х – числа студентов, успешно сдавших экзамен. Найти Е(Х).