Тема 2 Проекции прямой понятие о существенных свойствах

Тема 2 Проекции прямой понятие о существенных свойствах прямых линий, их классификации и взаимном положении

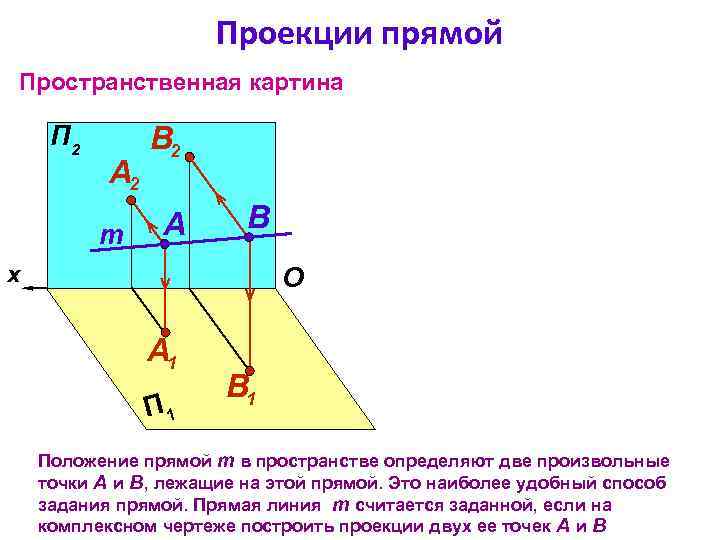Проекции прямой Пространственная картина П 2 А 2 m В 2 A B x O А 1 П 1 B 1 Положение прямой m в пространстве определяют две произвольные точки А и В, лежащие на этой прямой. Это наиболее удобный способ задания прямой. Прямая линия m считается заданной, если на комплексном чертеже построить проекции двух ее точек А и В

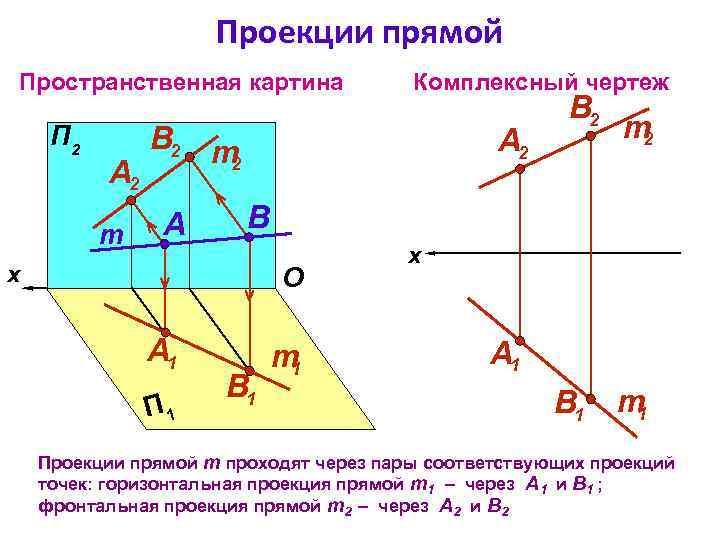Проекции прямой Пространственная картина П 2 А 2 m Комплексный чертеж В 2 m 2 A А 2 O П 1 m 2 B x А 1 B 2 B 1 m 1 x А 1 B 1 m 1 Проекции прямой m проходят через пары соответствующих проекций точек: горизонтальная проекция прямой m 1 – через А 1 и В 1 ; фронтальная проекция прямой m 2 – через А 2 и В 2

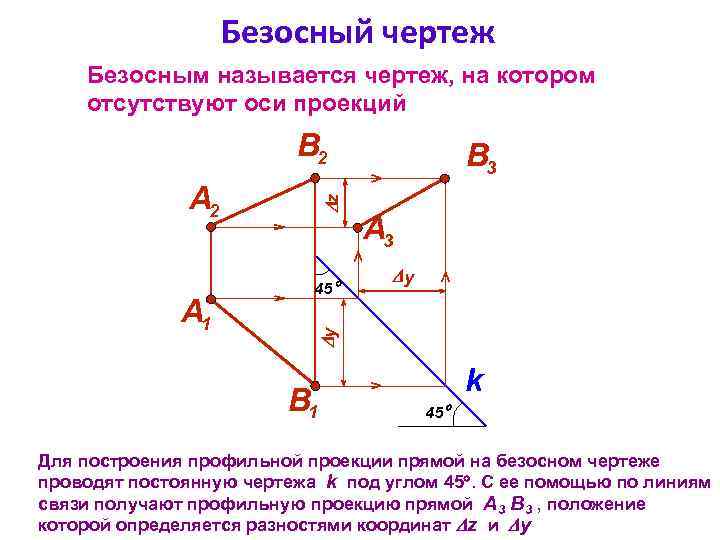Безосный чертеж Безосным называется чертеж, на котором отсутствуют оси проекций B 2 45 А 3 y y А 1 z А 2 B 3 B 1 k 45 Для построения профильной проекции прямой на безосном чертеже проводят постоянную чертежа k под углом 45. С ее помощью по линиям связи получают профильную проекцию прямой А 3 В 3 , положение которой определяется разностями координат z и y

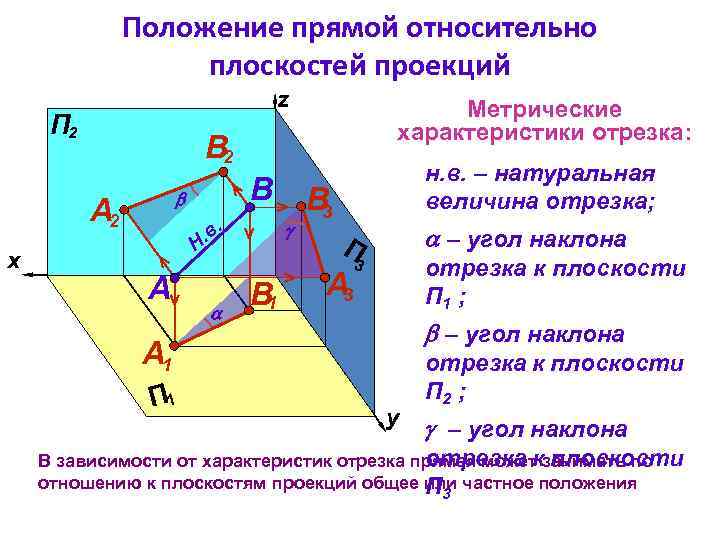Положение прямой относительно плоскостей проекций z П 2 В 2 B А 2 x Метрические характеристики отрезка: . в Н. A B 1 н. в. – натуральная величина отрезка; В 3 – угол наклона П 3 отрезка к плоcкости П 1 ; А 3 – угол наклона А 1 П 1 y отрезка к плоcкости П 2 ; – угол наклона отрезка к плоcкости В зависимости от характеристик отрезка прямая может занимать по отношению к плоскостям проекций общее или частное положения П 3

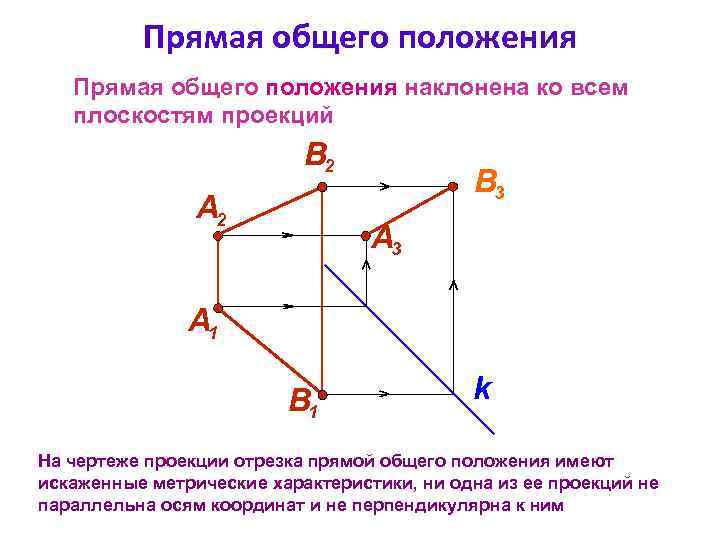Прямая общего положения наклонена ко всем плоскостям проекций B 2 А 2 B 3 А 1 B 1 k На чертеже проекции отрезка прямой общего положения имеют искаженные метрические характеристики, ни одна из ее проекций не параллельна осям координат и не перпендикулярна к ним

Прямые частного положения Прямая частного положения параллельна или перпендикулярна одной из плоскостей проекций Прямая, параллельная одной из плоскостей проекций, называется прямой уровня: Горизонтальная прямая уровня (горизонталь) h П 1 Фронтальная прямая уровня (фронталь) f П 2 Профильная прямая p П Прямая, перпендикулярная одной из плоскостей 3 проекций, называется проецирующей прямой: Горизонтально проецирующая прямая П 1 Фронтально проецирующая прямая П 2 Профильно проецирующая прямая П 3

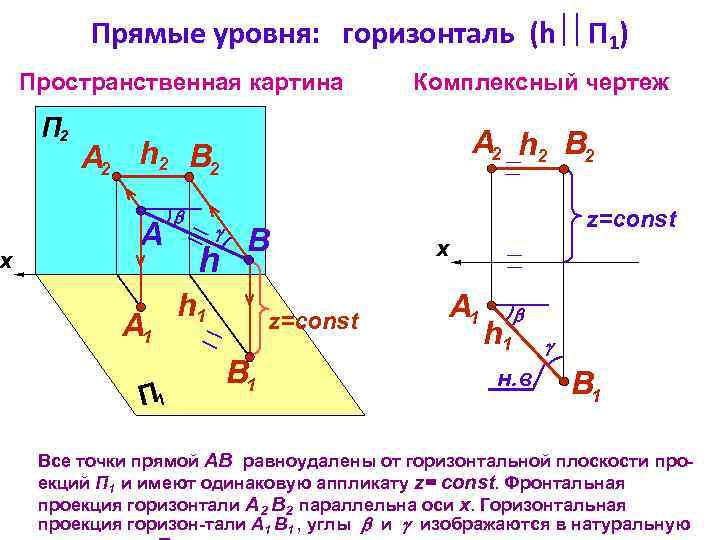x Прямые уровня: горизонталь (h П 1) Пространственная картина П 2 Комплексный чертеж А 2 h 2 В 2 A А 1 П 1 h B h 1 z=const B 1 z=const x А 1 h 1 н. в. B 1 Все точки прямой АВ равноудалены от горизонтальной плоскости проекций П 1 и имеют одинаковую аппликату z= const. Фронтальная проекция горизонтали А 2 В 2 параллельна оси х. Горизонтальная проекция горизон-тали А 1 В 1 , углы и изображаются в натуральную

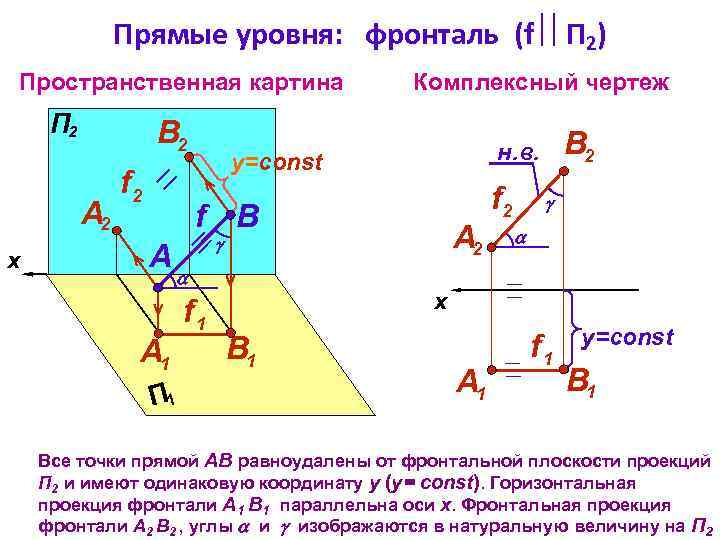Прямые уровня: фронталь (f П 2) Пространственная картина В 2 А 2 x f 2 y=const f B A П 1 А 2 f 2 f 1 А 1 В 2 н. в. x П 2 Комплексный чертеж B 1 А 1 f 1 y=const B 1 Все точки прямой АВ равноудалены от фронтальной плоскости проекций П 2 и имеют одинаковую координату y (y= const). Горизонтальная проекция фронтали А 1 В 1 параллельна оси х. Фронтальная проекция фронтали А 2 В 2 , углы и изображаются в натуральную величину на П 2

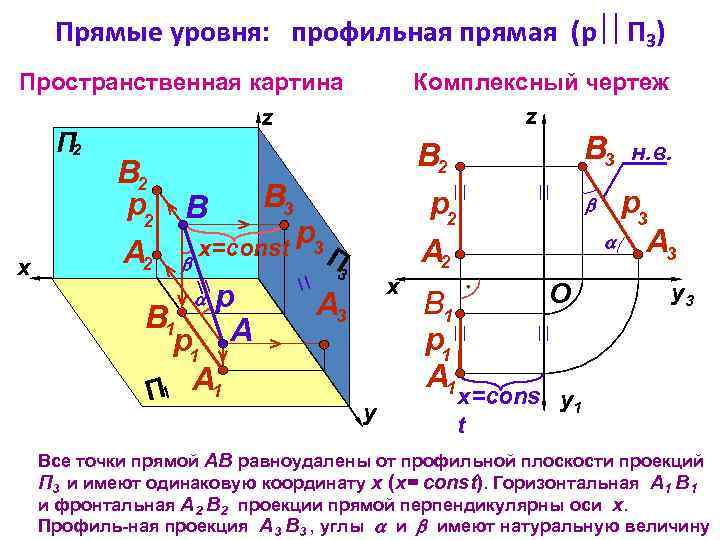Прямые уровня: профильная прямая (р П 3) Пространственная картина z П 2 x В 2 В 3 р2 B р x=const 3 П А 2 3 р А 3 B 1 р1 A П 1 А 1 Комплексный чертеж z В 2 р2 А 2 x y В 3 B 1 р1 А 1 O н. в. р3 А 3 y 3 x=cons y 1 t Все точки прямой АВ равноудалены от профильной плоскости проекций П 3 и имеют одинаковую координату х (х= const). Горизонтальная А 1 В 1 и фронтальная А 2 В 2 проекции прямой перпендикулярны оси х. Профиль-ная проекция А 3 В 3 , углы и имеют натуральную величину

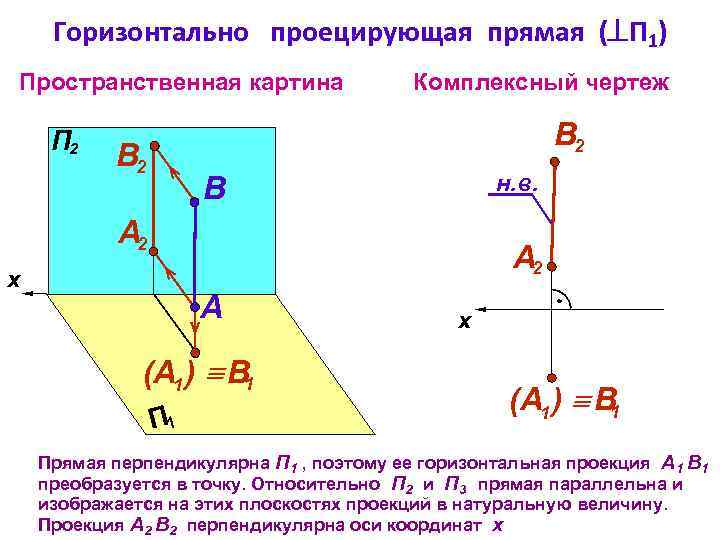Горизонтально проецирующая прямая ( П 1) Пространственная картина П 2 Комплексный чертеж В 2 н. в. B А 2 A (А 1 ) B 1 П 1 x x (А 1 ) B 1 Прямая перпендикулярна П 1 , поэтому ее горизонтальная проекция А 1 В 1 преобразуется в точку. Относительно П 2 и П 3 прямая параллельна и изображается на этих плоскостях проекций в натуральную величину. Проекция А 2 В 2 перпендикулярна оси координат х

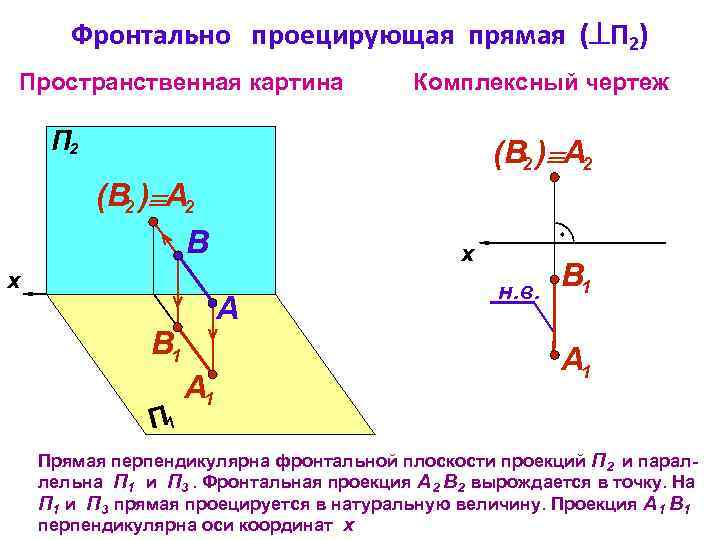Фронтально проецирующая прямая ( П 2) Пространственная картина Комплексный чертеж П 2 (В 2 ) А 2 B A B 1 П 1 x x А 1 н. в. B 1 А 1 Прямая перпендикулярна фронтальной плоскости проекций П 2 и параллельна П 1 и П 3. Фронтальная проекция А 2 В 2 вырождается в точку. На П 1 и П 3 прямая проецируется в натуральную величину. Проекция А 1 В 1 перпендикулярна оси координат х

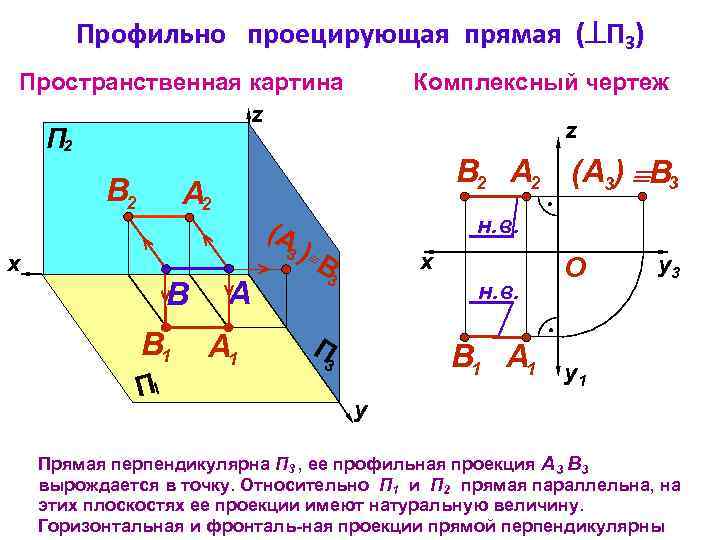Профильно проецирующая прямая ( П 3) Пространственная картина z Комплексный чертеж z П 2 В 2 B 2 А 2 (A 3) B 3 А 2 (А н. в. )В 3 3 B B 1 П 1 A А 1 x x П 3 н. в. B 1 А 1 O y 3 y 1 y Прямая перпендикулярна П 3 , ее профильная проекция А 3 В 3 вырождается в точку. Относительно П 1 и П 2 прямая параллельна, на этих плоскостях ее проекции имеют натуральную величину. Горизонтальная и фронталь-ная проекции прямой перпендикулярны

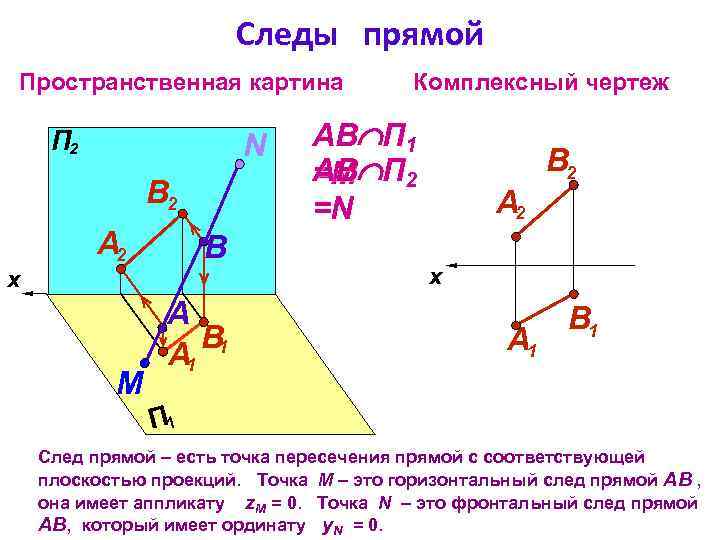Следы прямой Пространственная картина П 2 N В 2 А 2 Комплексный чертеж АВ П 1 АВ = М П 2 =N В 2 А 2 B x x M A B 1 А 1 B 1 П 1 След прямой – есть точка пересечения прямой с соответствующей плоскостью проекций. Точка М – это горизонтальный след прямой АВ , она имеет аппликату z. М = 0. Точка N – это фронтальный след прямой АВ, который имеет ординату y. N = 0.

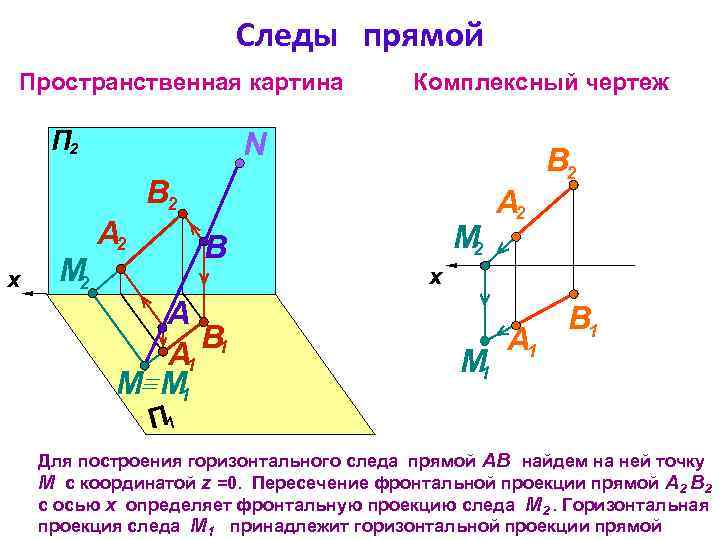Следы прямой Пространственная картина П 2 Комплексный чертеж N В 2 М 2 B x x А 2 A B 1 А 1 M M 1 М 1 А 1 B 1 П 1 Для построения горизонтального следа прямой АВ найдем на ней точку М с координатой z =0. Пересечение фронтальной проекции прямой А 2 В 2 с осью х определяет фронтальную проекцию следа M 2. Горизонтальная проекция следа М 1 принадлежит горизонтальной проекции прямой

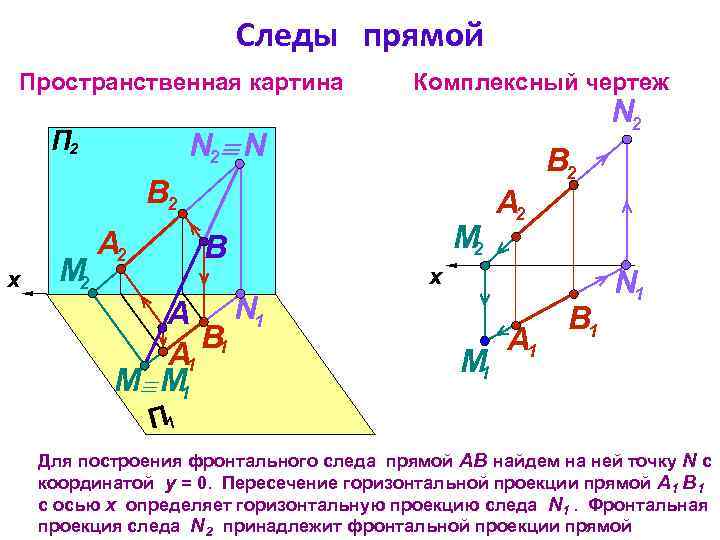Следы прямой Пространственная картина Комплексный чертеж N 2 N П 2 В 2 М 2 B A N 1 B 1 А 1 M M 1 x x А 2 М 1 А 1 B 1 N 1 П 1 Для построения фронтального следа прямой АВ найдем на ней точку N с координатой y = 0. Пересечение горизонтальной проекции прямой А 1 В 1 с осью х определяет горизонтальную проекцию следа N 1. Фронтальная проекция следа N 2 принадлежит фронтальной проекции прямой

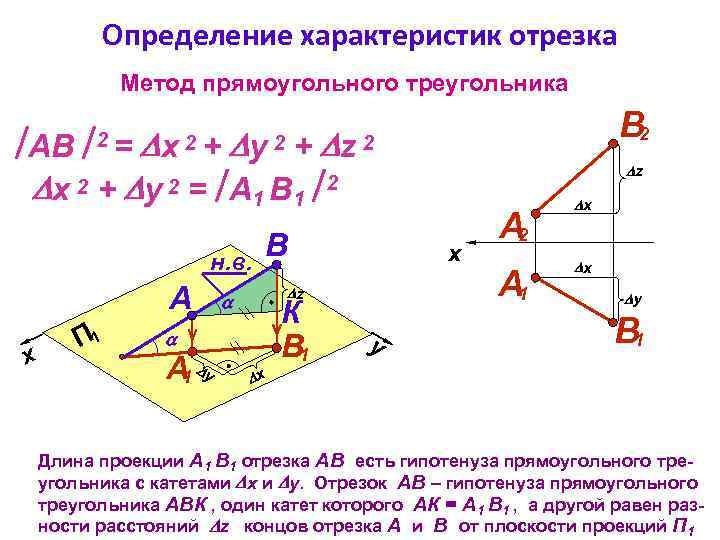Определение характеристик отрезка Метод прямоугольного треугольника В 2 АВ + x 2 + y 2 = А 1 В 1 2 x 2+ y 2 н. в. A x П 1 B z К B 1 А y 1 z 2 z x 2= y А 2 А 1 x x y B 1 x Длина проекции А 1 В 1 отрезка АВ есть гипотенуза прямоугольного треугольника с катетами x и y. Отрезок АВ – гипотенуза прямоугольного треугольника АВК , один катет которого АК = А 1 В 1 , а другой равен разности расстояний z концов отрезка А и В от плоскости проекций П 1

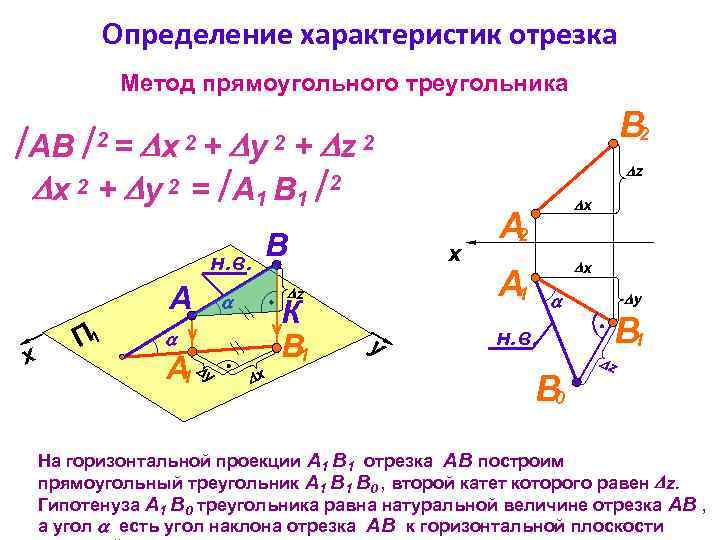Определение характеристик отрезка Метод прямоугольного треугольника В 2 АВ + x 2 + y 2 = А 1 В 1 2 x 2+ y 2 н. в. A x П 1 B z К B 1 А y 1 z 2 x z x 2= y x А 2 x А 1 н. в. B 0 y B 1 z На горизонтальной проекции А 1 В 1 отрезка АВ построим прямоугольный треугольник А 1 В 0 , второй катет которого равен z. Гипотенуза А 1 В 0 треугольника равна натуральной величине отрезка АВ , а угол есть угол наклона отрезка АВ к горизонтальной плоскости

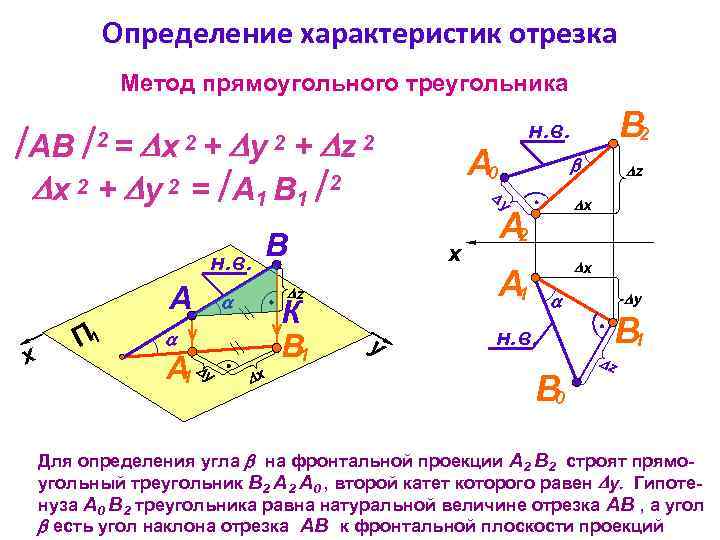Определение характеристик отрезка Метод прямоугольного треугольника АВ + x 2 + y 2 = А 1 В 1 2 x 2+ y 2 A x П 1 B z К B 1 А y 1 x y В 2 н. в. А 0 z x y н. в. z 2 x 2= А 2 x А 1 н. в. B 0 y B 1 z Для определения угла на фронтальной проекции А 2 В 2 строят прямоугольный треугольник В 2 А 0 , второй катет которого равен y. Гипотенуза А 0 В 2 треугольника равна натуральной величине отрезка АВ , а угол есть угол наклона отрезка АВ к фронтальной плоскости проекций

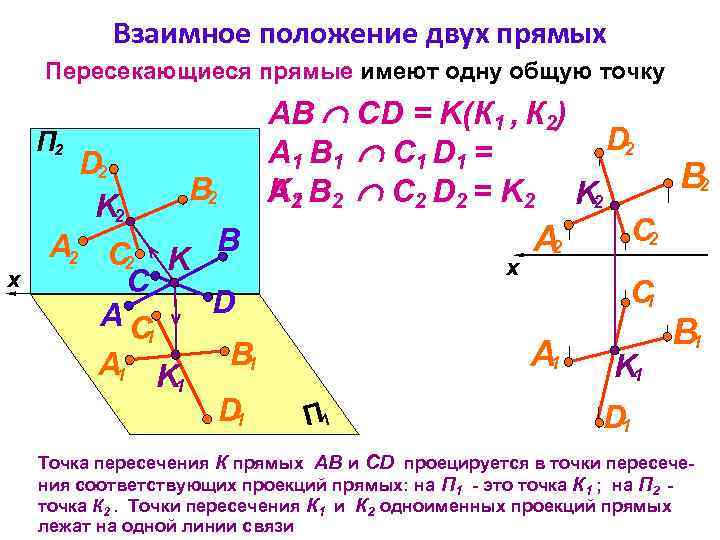Взаимное положение двух прямых Пересекающиеся прямые имеют одну общую точку x x АВ СD = K(К 1 , К 2) D 2 П 2 А 1 В 1 С 1 D 1 = D 2 В 2 K 1 А 2 В 2 С 2 D 2 = K 2 K 2 C 2 А 2 B А 2 C 2 K C C 1 D AC 1 B 1 А 1 K 1 D 1 П 1 D 1 Точка пересечения К прямых АВ и СD проецируется в точки пересечения соответствующих проекций прямых: на П 1 - это точка К 1 ; на П 2 точка К 2. Точки пересечения К 1 и К 2 одноименных проекций прямых лежат на одной линии связи

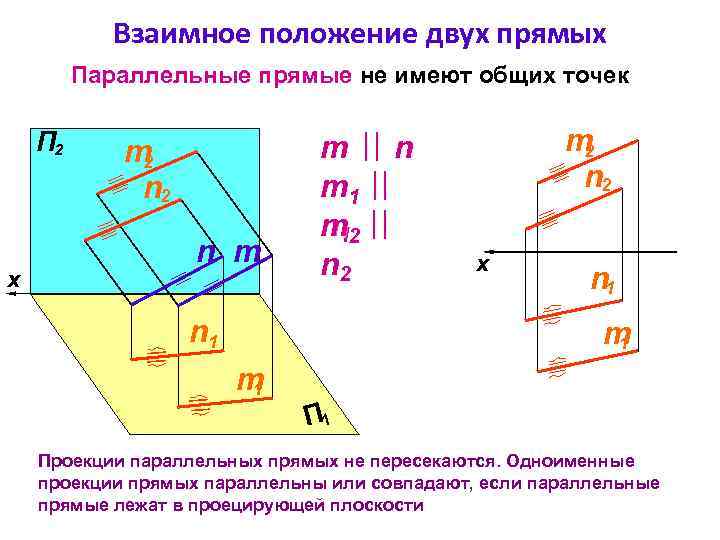Взаимное положение двух прямых Параллельные прямые не имеют общих точек x m 2 n m m n m 1 n 1 m 2 n 2 n 1 m 2 n 2 x П 2 n 1 m 1 Проекции параллельных прямых не пересекаются. Одноименные проекции прямых параллельны или совпадают, если параллельные прямые лежат в проецирующей плоскости

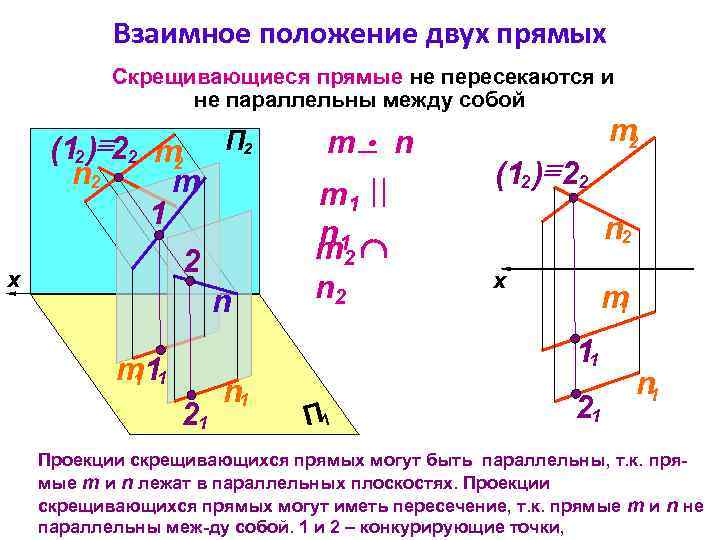Взаимное положение двух прямых Скрещивающиеся прямые не пересекаются и не параллельны между собой 1 m m 1 n 1 m 2 x m n 2 n n 2 m 2 (12 ) 22 n 2 x n 2 П 2 (12 ) 22 m 1 11 m 11 1 21 n 1 Проекции скрещивающихся прямых могут быть параллельны, т. к. прямые m и n лежат в параллельных плоскостях. Проекции скрещивающихся прямых могут иметь пересечение, т. к. прямые m и n не параллельны меж-ду собой. 1 и 2 – конкурирующие точки,

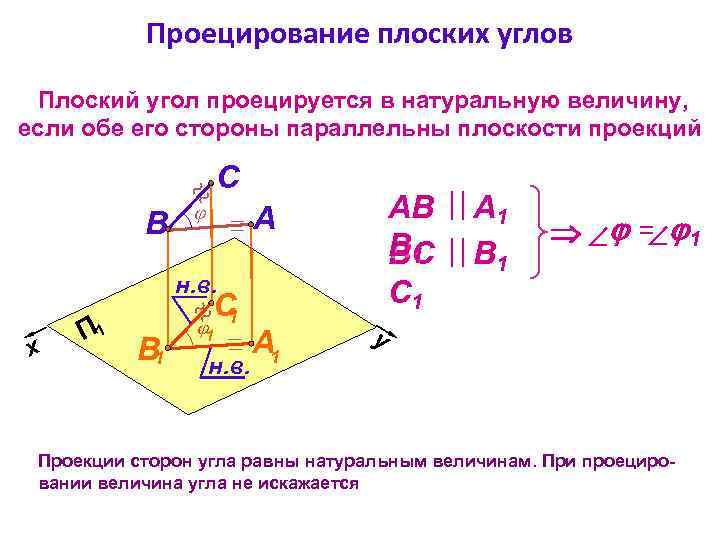Проецирование плоских углов Плоский угол проецируется в натуральную величину, если обе его стороны параллельны плоскости проекций C B АВ А 1 В 1 B 1 BC C 1 A н. в. x П 1 C 1 B 1 1 н. в. А 1 = 1 y Проекции сторон угла равны натуральным величинам. При проецировании величина угла не искажается

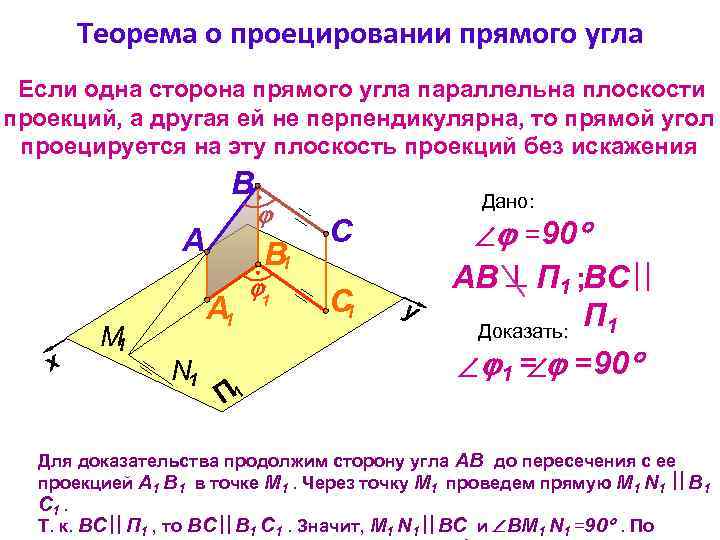Теорема о проецировании прямого угла Если одна сторона прямого угла параллельна плоскости проекций, а другая ей не перпендикулярна, то прямой угол проецируется на эту плоскость проекций без искажения B A x М 1 B 1 А 1 N 1 П 1 1 Дано: C C 1 y =90 АВ П 1 ; BC П 1 1 = =90 Доказать: Для доказательства продолжим сторону угла АВ до пересечения с ее проекцией А 1 В 1 в точке М 1. Через точку М 1 проведем прямую М 1 N 1 В 1 C 1. Т. к. BC П 1 , то BC В 1 С 1. Значит, М 1 N 1 ВС и BM 1 N 1 =90 . По

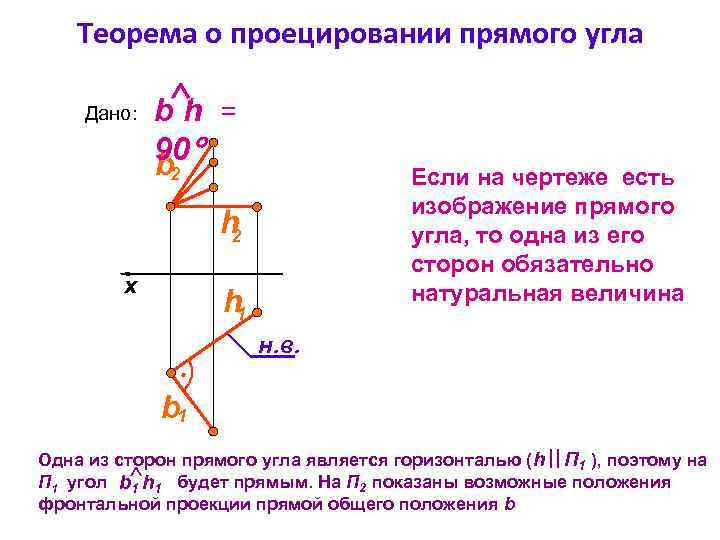Теорема о проецировании прямого угла Дано: bh = 90 b 2 Если на чертеже есть изображение прямого угла, то одна из его сторон обязательно натуральная величина h 2 x h 1 н. в. b 1 Одна из сторон прямого угла является горизонталью (h П 1 ), поэтому на П 1 угол b 1 h 1 будет прямым. На П 2 показаны возможные положения фронтальной проекции прямой общего положения b

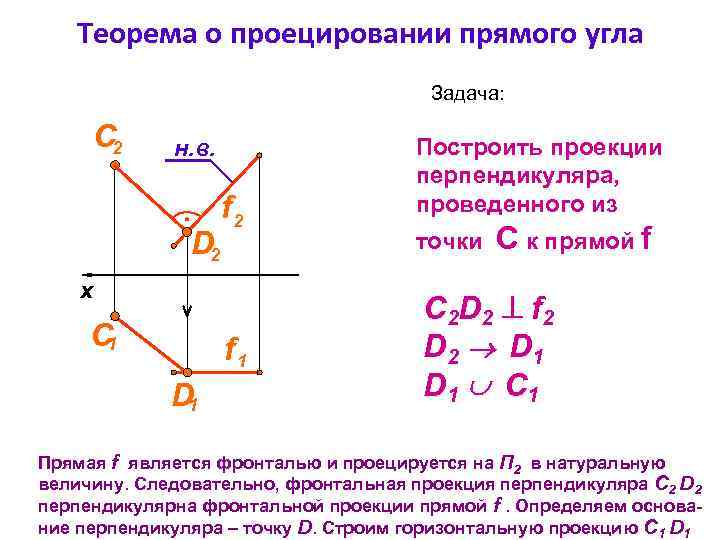Теорема о проецировании прямого угла Задача: C 2 н. в. D 2 f 2 x С 1 f 1 D 1 Построить проекции перпендикуляра, проведенного из точки С к прямой f C 2 D 2 f 2 D 2 D 1 C 1 Прямая f является фронталью и проецируется на П 2 в натуральную величину. Следовательно, фронтальная проекция перпендикуляра С 2 D 2 перпендикулярна фронтальной проекции прямой f. Определяем основание перпендикуляра – точку D. Строим горизонтальную проекцию С 1 D 1

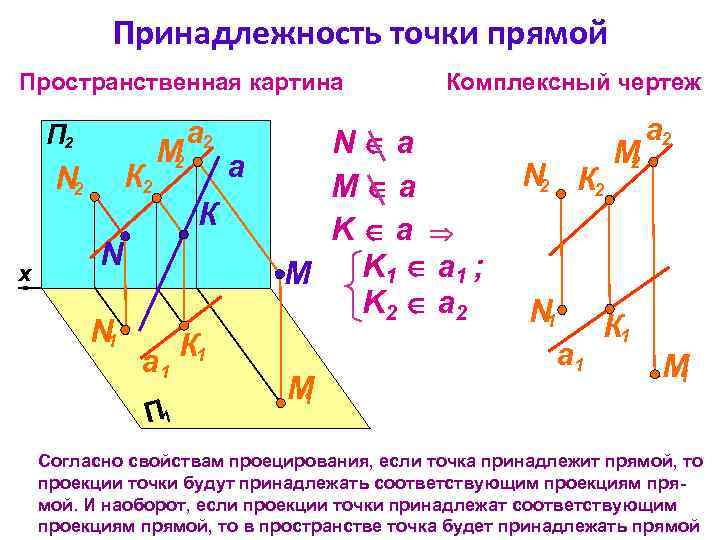Принадлежность точки прямой Пространственная картина П 2 К 2 N 2 x М 2 а 2 К N N 1 К 1 а 1 П 1 а Комплексный чертеж N a M a K a K 1 a 1 ; M K 2 a 2 M 1 N 2 К 2 N 1 а 1 М 2 а 2 К 1 M 1 Согласно свойствам проецирования, если точка принадлежит прямой, то проекции точки будут принадлежать соответствующим проекциям прямой. И наоборот, если проекции точки принадлежат соответствующим проекциям прямой, то в пространстве точка будет принадлежать прямой

Вопросы для самопроверки 1. Сколько точек однозначно определяют положение прямой в пространстве? а) одна б) две в) бесчисленное множество 2. Если отрезок прямой параллелен плоскости проекций, то длина его проекции на этой плоскости… а) искажается б) будет точкой в) равна длине отрезка 3. Если прямая перпендикулярна плоскости проекций, то ее проекцией на эту плоскость будет… а) прямая б) точка 4. Может ли прямая общего положения быть параллельной или перпендикулярной одной из основных плоскостей проекций? а) да б) нет

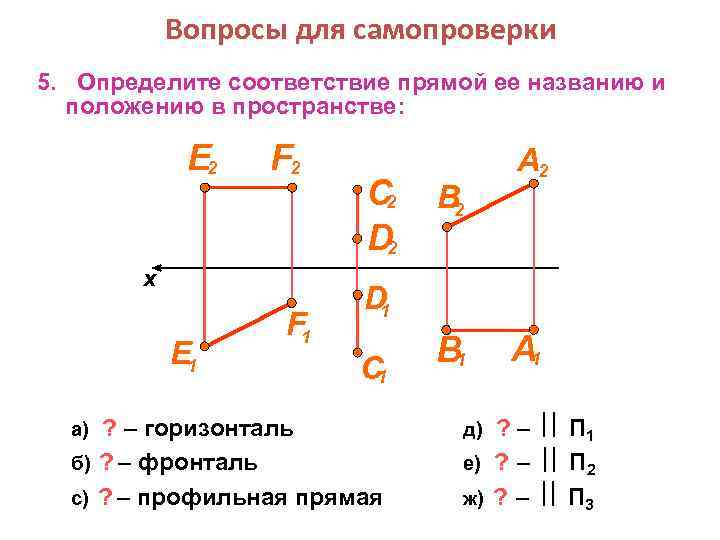Вопросы для самопроверки 5. Определите соответствие прямой ее названию и положению в пространстве: E 2 F 2 x E 1 F 1 C 2 D 1 C 1 ? – горизонталь б) ? – фронталь с) ? – профильная прямая а) В 2 A 2 B 1 А 1 ? – е) ? – ж) ? – д) П 1 П 2 П 3

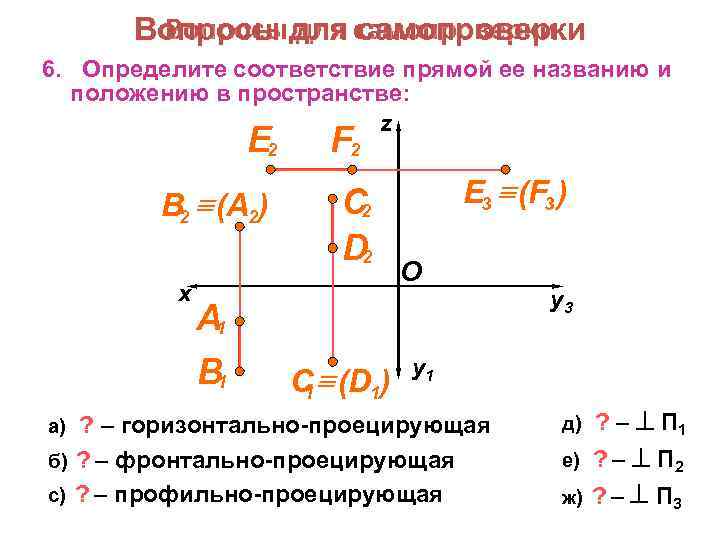Вопросы для самопроверки 6. Определите соответствие прямой ее названию и положению в пространстве: z E 2 В 2 (A 2) x А 1 B 1 F 2 C 2 D 2 C (D 1) 1 E 3 (F 3 ) O y 1 ? – горизонтально-проецирующая б) ? – фронтально-проецирующая с) ? – профильно-проецирующая а) y 3 д) ? – П 1 е) ? – П 2 ж) ? – П 3

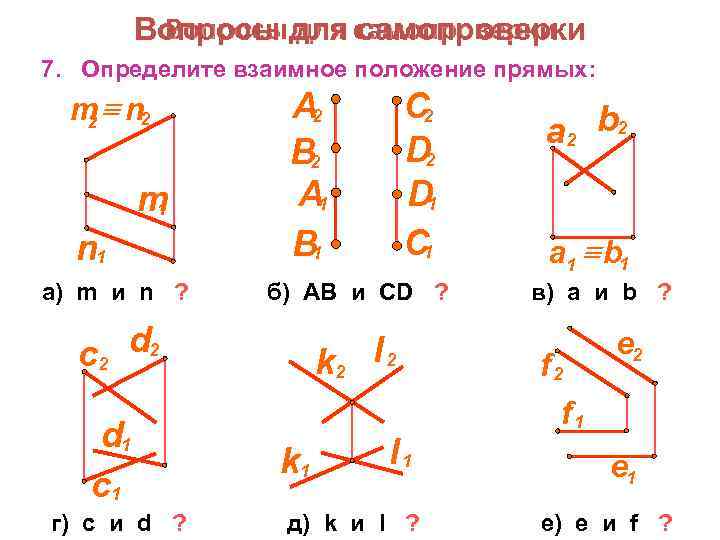Вопросы для самопроверки 7. Определите взаимное положение прямых: m n 2 2 m 1 n 1 а) m и n ? А 2 B 2 А 1 B 1 б) AB и CD ? d 2 c 2 d 1 c 1 г) c и d ? C 2 D 1 C 1 k 2 k 1 l 2 l 1 д) k и l ? a 2 b 2 a 1 b 1 в) a и b ? f 2 f 1 e 2 e 1 е) e и f ?

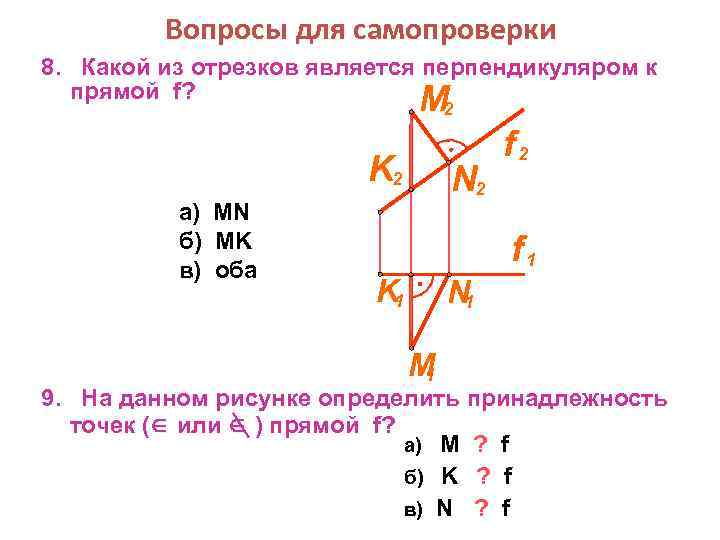Вопросы для самопроверки 8. Какой из отрезков является перпендикуляром к прямой f? M 2 K 2 а) MN б) MK в) оба N 2 f 1 K 1 N 1 M 1 9. На данном рисунке определить принадлежность точек ( или ) прямой f? а) М ? f б) K ? f в) N ? f