Тема 2. Параметры полета ракеты.pptx
- Количество слайдов: 75
 Тема 2. Параметры полета ракеты
Тема 2. Параметры полета ракеты
 Понятие о математическом моделировании движения ракет
Понятие о математическом моделировании движения ракет
 Для решения практических задач могут использоваться как теоретические, так и экспериментальные методы. В баллистике ракет использование летного эксперимента для решения таких задач весьма ограничено и часто в принципе невозможно. Это обусловлено следующими обстоятельствами:
Для решения практических задач могут использоваться как теоретические, так и экспериментальные методы. В баллистике ракет использование летного эксперимента для решения таких задач весьма ограничено и часто в принципе невозможно. Это обусловлено следующими обстоятельствами:
 - подготовка и проведение летного эксперимента приводит к фактическому уничтожению испытуемого образца ракеты; - большие материальные затраты на проведение летного эксперимента; - большие дальности полета, при которых ни запланированная цель, ни реальная точка падения БЧ не видны; - большое влияние возмущающих факторов, различное при каждом пуске, что исключает возможность пролонгации их влияния на последующие пуски;
- подготовка и проведение летного эксперимента приводит к фактическому уничтожению испытуемого образца ракеты; - большие материальные затраты на проведение летного эксперимента; - большие дальности полета, при которых ни запланированная цель, ни реальная точка падения БЧ не видны; - большое влияние возмущающих факторов, различное при каждом пуске, что исключает возможность пролонгации их влияния на последующие пуски;
 - большие временные затраты на подготовку и проведение каждого эксперимента.
- большие временные затраты на подготовку и проведение каждого эксперимента.
 При решении практических задач баллистики ракет физическое моделирование полета (летный эксперимент) заменяется математическим моделированием, т. е. математическим расчетом параметров движения
При решении практических задач баллистики ракет физическое моделирование полета (летный эксперимент) заменяется математическим моделированием, т. е. математическим расчетом параметров движения
 Такое математическое моделирование иногда называют «электронным выстрелом» , так как проводится на ЭЦВМ. В результате основным методом решения всех практических задач в баллистике ракет является метод математического моделирования полета при постановке минимального числа летных экспериментов.
Такое математическое моделирование иногда называют «электронным выстрелом» , так как проводится на ЭЦВМ. В результате основным методом решения всех практических задач в баллистике ракет является метод математического моделирования полета при постановке минимального числа летных экспериментов.
 Методы математического моделирования, кроме автоматизации численного анализа полета, позволяют сочетать теоретические исследования с экспериментальными. Они дают возможность проведения частичного эксперимента, т. е. такого эксперимента, в котором движение ракеты имитируется моделью, а система управления или отдельные ее приборы работают также, как и при действительном полете ракет.
Методы математического моделирования, кроме автоматизации численного анализа полета, позволяют сочетать теоретические исследования с экспериментальными. Они дают возможность проведения частичного эксперимента, т. е. такого эксперимента, в котором движение ракеты имитируется моделью, а система управления или отдельные ее приборы работают также, как и при действительном полете ракет.
 При таком частичном эксперименте дорогостоящие приборы системы управления не уничтожаются, а остаются невредимыми.
При таком частичном эксперименте дорогостоящие приборы системы управления не уничтожаются, а остаются невредимыми.
 Однако полет ракет и их БЧ является весьма сложным процессом так как подвержен влиянию большого числа различных факторов – случайных, трудно поддающихся математическому описанию. Поэтому любое математическое моделирование полета проводится лишь в некоторых идеализированных условиях. Степень идеализации зависит от условий решаемой задачи и может быть различной.
Однако полет ракет и их БЧ является весьма сложным процессом так как подвержен влиянию большого числа различных факторов – случайных, трудно поддающихся математическому описанию. Поэтому любое математическое моделирование полета проводится лишь в некоторых идеализированных условиях. Степень идеализации зависит от условий решаемой задачи и может быть различной.
 В связи с этим для математического моделирования полета ракет и БЧ создаются специальные математические модели, отражающие реальный полет с различной степенью точности.
В связи с этим для математического моделирования полета ракет и БЧ создаются специальные математические модели, отражающие реальный полет с различной степенью точности.
 Математическая модель движения представляет собой объективную схематизацию действительного движения объекта в форме, позволяющей проводить различные теоретические исследования и необходимые вычисления для решения поставленной задачи.
Математическая модель движения представляет собой объективную схематизацию действительного движения объекта в форме, позволяющей проводить различные теоретические исследования и необходимые вычисления для решения поставленной задачи.
 Такой формой обычно являются: - системы дифференциальных уравнений (обыкновенных или в частных производных), разрабатываемые в рамках теоретической механики и имеющие смысл уравнений движения объекта; - системы конечных аналитических соотношений, если схема полета позволяет получить аналитическое решение уравнений движения.
Такой формой обычно являются: - системы дифференциальных уравнений (обыкновенных или в частных производных), разрабатываемые в рамках теоретической механики и имеющие смысл уравнений движения объекта; - системы конечных аналитических соотношений, если схема полета позволяет получить аналитическое решение уравнений движения.
 Конкретный вид математической модели движения определяется принятыми при разработке модели схемами ЛА как механической системы, внешней среды, определяющей силовое воздействие на ЛА, а также системы отсчета и выбранной системы координат.
Конкретный вид математической модели движения определяется принятыми при разработке модели схемами ЛА как механической системы, внешней среды, определяющей силовое воздействие на ЛА, а также системы отсчета и выбранной системы координат.
 Выбор модели движения диктуется задачами проводимых исследований и неоднозначен. При этом к моделям часто предъявляются противоречивые требования - адекватности, точности, простоты, наглядности и др. Поэтому в каждой конкретной технической задаче обоснование и окончательный выбор модели является результатом компромисса и представляет собой важный этап процесса моделирования полета.
Выбор модели движения диктуется задачами проводимых исследований и неоднозначен. При этом к моделям часто предъявляются противоречивые требования - адекватности, точности, простоты, наглядности и др. Поэтому в каждой конкретной технической задаче обоснование и окончательный выбор модели является результатом компромисса и представляет собой важный этап процесса моделирования полета.
 Этим же обстоятельством объясняется и наличие большого числа различных математических моделей движения, используемых при решении практических задач.
Этим же обстоятельством объясняется и наличие большого числа различных математических моделей движения, используемых при решении практических задач.
 Все эти модели можно разделить на два вида: детерминированные и стохастические.
Все эти модели можно разделить на два вида: детерминированные и стохастические.
 К детерминированным моделям относят модели, для которых силы и моменты, действующие на объект, имеют только детерминированную составляющую. Это означает, что характер зависимости этой составляющей от параметров движения, времени и условий полета известен заранее.
К детерминированным моделям относят модели, для которых силы и моменты, действующие на объект, имеют только детерминированную составляющую. Это означает, что характер зависимости этой составляющей от параметров движения, времени и условий полета известен заранее.
 К стохастическим относят модели, для которых связь между параметрами движения и временем известна лишь приближенно и может быть представлена некоторым распределением вероятности. Для таких моделей предполагается, что все или некоторые компоненты вектора характеристик, определяющих силы и моменты, действующие на объект, содержат случайную составляющую наряду с детерминированной.
К стохастическим относят модели, для которых связь между параметрами движения и временем известна лишь приближенно и может быть представлена некоторым распределением вероятности. Для таких моделей предполагается, что все или некоторые компоненты вектора характеристик, определяющих силы и моменты, действующие на объект, содержат случайную составляющую наряду с детерминированной.
 Как детерминированные, так и стохастические модели могут быть представлены в дифференциальном или конечном аналитическом виде в зависимости от того, допускают или не допускают дифференциальные уравнения движения объекта получение конечного аналитического решения.
Как детерминированные, так и стохастические модели могут быть представлены в дифференциальном или конечном аналитическом виде в зависимости от того, допускают или не допускают дифференциальные уравнения движения объекта получение конечного аналитического решения.
 Для проведения математического моделирования полета модель движения должна быть дополнена начальными условиями, определяющими начальное состояние ракеты, или соотношениями для их расчета, системой ограничений или связей, определяющих множество допустимых значений параметров движения, параметров ракеты и ее системы управления, а также условиями или алгоритмом определения конечного состояния, т. е. окончания процесса моделирования.
Для проведения математического моделирования полета модель движения должна быть дополнена начальными условиями, определяющими начальное состояние ракеты, или соотношениями для их расчета, системой ограничений или связей, определяющих множество допустимых значений параметров движения, параметров ракеты и ее системы управления, а также условиями или алгоритмом определения конечного состояния, т. е. окончания процесса моделирования.
 В целом численное моделирование полета предполагает последовательное выполнение следующих основных операций:
В целом численное моделирование полета предполагает последовательное выполнение следующих основных операций:
 1. Схематизация полета, включающая в себя схематизацию ракеты как механической системы, системы отсчета и условий полета, а также схематизацию системы управления полетом.
1. Схематизация полета, включающая в себя схематизацию ракеты как механической системы, системы отсчета и условий полета, а также схематизацию системы управления полетом.
 2. Запись уравнений движения в скалярной форме при соответствующем выборе систем координат. 3. Задание начальных условий для системы дифференциальных уравнений движения или соотношений для их расчета.
2. Запись уравнений движения в скалярной форме при соответствующем выборе систем координат. 3. Задание начальных условий для системы дифференциальных уравнений движения или соотношений для их расчета.
 4. Задание исходных данных по ракете и ее системе управления, включающих энергетические, массово-инерционные, аэродинамические, геометрические и другие характеристики.
4. Задание исходных данных по ракете и ее системе управления, включающих энергетические, массово-инерционные, аэродинамические, геометрические и другие характеристики.
 5. Задание системы возможных ограничений или связей на параметры движения или параметры управления, определяющих область их допустимых значений.
5. Задание системы возможных ограничений или связей на параметры движения или параметры управления, определяющих область их допустимых значений.
 6. Выбор и обоснование метода численного интегрирования уравнений движения или аналитических представлений полета на отдельных участках траектории, величины шага интегрирования на активном и пассивном участках траектории и условий окончания процесса моделирования.
6. Выбор и обоснование метода численного интегрирования уравнений движения или аналитических представлений полета на отдельных участках траектории, величины шага интегрирования на активном и пассивном участках траектории и условий окончания процесса моделирования.
 7. Обоснование необходимого количества численных экспериментов для выявления требуемых закономерностей полета или получения решения поставленной задачи.
7. Обоснование необходимого количества численных экспериментов для выявления требуемых закономерностей полета или получения решения поставленной задачи.
 8. Проведение численных экспериментов и представление их результатов в требуемой по условиям задачи форме с указанием границ или рамок их возможного использования.
8. Проведение численных экспериментов и представление их результатов в требуемой по условиям задачи форме с указанием границ или рамок их возможного использования.
 В зависимости от конкретной технической задачи, решаемой путем моделирования полета, содержание вышеуказанных этапов может быть конкретизировано или дополнено другими операциями.
В зависимости от конкретной технической задачи, решаемой путем моделирования полета, содержание вышеуказанных этапов может быть конкретизировано или дополнено другими операциями.
 Полет и его характеристики
Полет и его характеристики
 Полет – это движение материального тела, называемого ЛА, над поверхностью Земли в атмосфере или за ее пределами в космическом пространстве. Полет является частным видом механического движения, называемого перемещением материального тела в пространстве и во времени. Для задания полета, его математического описания и характеристики могут быть использованы основные понятия и подходы теоретической механики.
Полет – это движение материального тела, называемого ЛА, над поверхностью Земли в атмосфере или за ее пределами в космическом пространстве. Полет является частным видом механического движения, называемого перемещением материального тела в пространстве и во времени. Для задания полета, его математического описания и характеристики могут быть использованы основные понятия и подходы теоретической механики.
 Для полета реальный ЛА должен быть представлен в виде некоторого абстрактного механического объекта (материальная точка, система материальных точек, твердое тело и т. д. ), к которому применимы общие законы механики.
Для полета реальный ЛА должен быть представлен в виде некоторого абстрактного механического объекта (материальная точка, система материальных точек, твердое тело и т. д. ), к которому применимы общие законы механики.
 Такое представление ЛА называется схематизацией. Будем исходить из того, что ракета или ее БЧ могут быть представлены схемой твердого тела. В теоретической механике произвольное перемещение твердого тела представляется в виде совокупности поступательного движения некоторого полюса и вращательного движения тела относительно этого полюса.
Такое представление ЛА называется схематизацией. Будем исходить из того, что ракета или ее БЧ могут быть представлены схемой твердого тела. В теоретической механике произвольное перемещение твердого тела представляется в виде совокупности поступательного движения некоторого полюса и вращательного движения тела относительно этого полюса.
 В качестве полюса может быть выбрана произвольная точка тела. Обычно в качестве полюса принимают ЦМ тела. В этом случае уравнения движения имеют наиболее простой вид.
В качестве полюса может быть выбрана произвольная точка тела. Обычно в качестве полюса принимают ЦМ тела. В этом случае уравнения движения имеют наиболее простой вид.
 Поступательным движением твердого тела называют такое движение, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе. При этом движении скорости и ускорения всех точек тела для любого момента времени равны между собой. Поэтому движение ЛА может быть полностью определено движением одной точки, например, движением ЦМ.
Поступательным движением твердого тела называют такое движение, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе. При этом движении скорости и ускорения всех точек тела для любого момента времени равны между собой. Поэтому движение ЛА может быть полностью определено движением одной точки, например, движением ЦМ.
 Вращательным движением твердого тела называется движение, при котором какие-либо две точки тела остаются неподвижными в каждый текущий момент времени, т. е. происходит вращение тела вокруг некоторой мгновенной оси.
Вращательным движением твердого тела называется движение, при котором какие-либо две точки тела остаются неподвижными в каждый текущий момент времени, т. е. происходит вращение тела вокруг некоторой мгновенной оси.
 Физические величины, характеризующие положение и ориентацию ЛА в пространстве и их изменение во времени, называют параметрами движения. Как правило, к ним относят линейные и угловые координаты, составляющие векторов линейных и угловых скоростей и ускорений ЛА в той или иной системе координат.
Физические величины, характеризующие положение и ориентацию ЛА в пространстве и их изменение во времени, называют параметрами движения. Как правило, к ним относят линейные и угловые координаты, составляющие векторов линейных и угловых скоростей и ускорений ЛА в той или иной системе координат.
 При этом величины, характеризующие движение центра масс ЛА, называют параметрами поступательного движения, а величины, характеризующие движение ЛА вокруг ЦМ - параметрами вращательного движения.
При этом величины, характеризующие движение центра масс ЛА, называют параметрами поступательного движения, а величины, характеризующие движение ЛА вокруг ЦМ - параметрами вращательного движения.
 В общем случае параметры движения отражают его различные стороны и в соответствии с этим подразделяются на геометрические, кинематические и динамические.
В общем случае параметры движения отражают его различные стороны и в соответствии с этим подразделяются на геометрические, кинематические и динамические.
 Под геометрическими параметрами понимают параметры движения, характеризующие геометрические свойства полета и определяющие составляющие вектора положения ЛА в некоторой системе координат. Это параметры ориентации ЛА (углы Эйлера, направляющие косинусы и т. д. ) в заданный момент времени.
Под геометрическими параметрами понимают параметры движения, характеризующие геометрические свойства полета и определяющие составляющие вектора положения ЛА в некоторой системе координат. Это параметры ориентации ЛА (углы Эйлера, направляющие косинусы и т. д. ) в заданный момент времени.
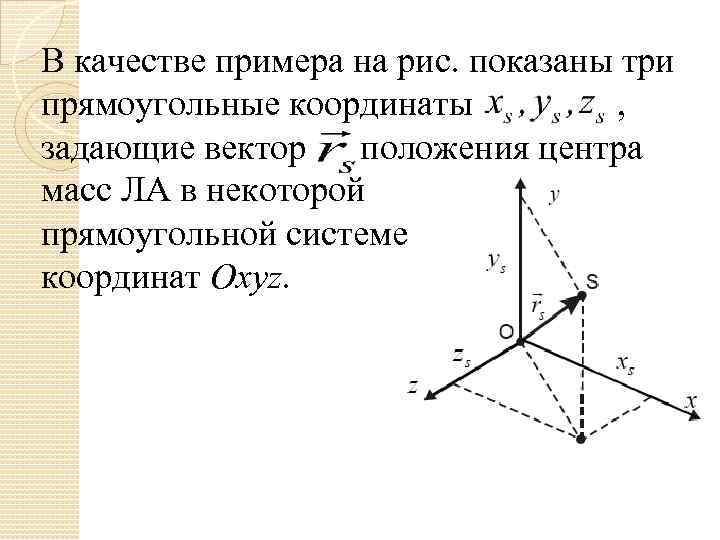 В качестве примера на рис. показаны три прямоугольные координаты , задающие вектор положения центра масс ЛА в некоторой прямоугольной системе координат Oxyz.
В качестве примера на рис. показаны три прямоугольные координаты , задающие вектор положения центра масс ЛА в некоторой прямоугольной системе координат Oxyz.
 Кинематические параметры движения характеризуют кинематические свойства полета ЛА без учета его массовоинерционных характеристик и действующих на ЛА сил и определяют компоненты векторов линейной и угловой скоростей ЛА в различных системах координат.
Кинематические параметры движения характеризуют кинематические свойства полета ЛА без учета его массовоинерционных характеристик и действующих на ЛА сил и определяют компоненты векторов линейной и угловой скоростей ЛА в различных системах координат.
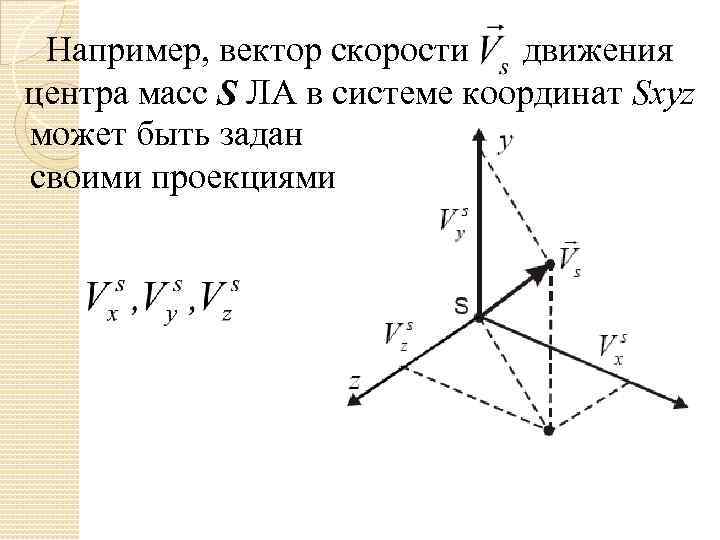 Например, вектор скорости движения центра масс S ЛА в системе координат Sxyz может быть задан своими проекциями
Например, вектор скорости движения центра масс S ЛА в системе координат Sxyz может быть задан своими проекциями
 Динамические параметры движения отражают динамические свойства полета, обусловленные действующими на ЛА силами и моментами и его массовоинерционными характеристиками, и определяют компоненты векторов линейного и углового ускорений ЛА.
Динамические параметры движения отражают динамические свойства полета, обусловленные действующими на ЛА силами и моментами и его массовоинерционными характеристиками, и определяют компоненты векторов линейного и углового ускорений ЛА.
 Геометрические параметры движения являются интегральными по отношению к кинематическим параметрам. Кинематические параметры являются интегральными по отношению к динамическим параметрам.
Геометрические параметры движения являются интегральными по отношению к кинематическим параметрам. Кинематические параметры являются интегральными по отношению к динамическим параметрам.
 Все они связаны между собой дифференциальными зависимостями где - вектор параметров угловой ориентации ЛА в пространстве; - вектор угловой скорости ЛА; - векторы линейного и углового ускорений.
Все они связаны между собой дифференциальными зависимостями где - вектор параметров угловой ориентации ЛА в пространстве; - вектор угловой скорости ЛА; - векторы линейного и углового ускорений.
 При математическом описании и анализе полета используется большое число различных параметров движения, задаваемых в различных СК. Однако число независимых параметров в каждой из названных групп определяется числом степеней свободы ракеты.
При математическом описании и анализе полета используется большое число различных параметров движения, задаваемых в различных СК. Однако число независимых параметров в каждой из названных групп определяется числом степеней свободы ракеты.
 Под числом степеней свободы понимают минимальное число независимых параметров (координат), однозначно определяющих положение тела в пространстве.
Под числом степеней свободы понимают минимальное число независимых параметров (координат), однозначно определяющих положение тела в пространстве.
 Независимость параметров следует понимать в том смысле, что ни один из них не может быть выражен через другие. Для материальной точки число степеней свободы равно трем, так как ее положение в пространстве можно однозначно задать с помощью трех координат. Абсолютно твердое тело имеет шесть степеней свободы: три степени свободы поступательного движения и три вращательного движения.
Независимость параметров следует понимать в том смысле, что ни один из них не может быть выражен через другие. Для материальной точки число степеней свободы равно трем, так как ее положение в пространстве можно однозначно задать с помощью трех координат. Абсолютно твердое тело имеет шесть степеней свободы: три степени свободы поступательного движения и три вращательного движения.
 Движение ЛА можно считать кинематически заданным, если известен закон изменения параметров движения во времени (2)
Движение ЛА можно считать кинематически заданным, если известен закон изменения параметров движения во времени (2)
 Однако в силу дифференциальной зависимости между геометрическими, кинематическими и динамическими параметрами движения установить этот закон можно только через дифференциальные уравнения, которые называют уравнениями движения.
Однако в силу дифференциальной зависимости между геометрическими, кинематическими и динамическими параметрами движения установить этот закон можно только через дифференциальные уравнения, которые называют уравнениями движения.
 Уравнения движения являются основной частью математической модели движения. Задача записи этих уравнений представляет собой задачу математического описания полета.
Уравнения движения являются основной частью математической модели движения. Задача записи этих уравнений представляет собой задачу математического описания полета.
 Получающаяся в результате система обыкновенных дифференциальных уравнений движения, приведенная к нормальной форме, обычно записывается в следующем стандартном функциональном виде: где n - порядок системы (3) уравнении, равный удвоенному числу степеней свободы ЛА; t - время, являющееся независимой переменной; - неизвестные переменные, зависимые от времени; - первые производные по времени от соответствующих переменных.
Получающаяся в результате система обыкновенных дифференциальных уравнений движения, приведенная к нормальной форме, обычно записывается в следующем стандартном функциональном виде: где n - порядок системы (3) уравнении, равный удвоенному числу степеней свободы ЛА; t - время, являющееся независимой переменной; - неизвестные переменные, зависимые от времени; - первые производные по времени от соответствующих переменных.
 Зависимые переменные представляют собой линейные и угловые координаты и составляющие векторов линейной и угловой скоростей ЛА, т. е. совокупность геометрических и кинематических параметров движения. Они полностью определяют положение ЛА и его скорость в текущий момент времени, поэтому их также называют параметрами состояния, или фазовыми координатами.
Зависимые переменные представляют собой линейные и угловые координаты и составляющие векторов линейной и угловой скоростей ЛА, т. е. совокупность геометрических и кинематических параметров движения. Они полностью определяют положение ЛА и его скорость в текущий момент времени, поэтому их также называют параметрами состояния, или фазовыми координатами.
 Соответствующая числу степеней свободы совокупность независимых параметров состояния образует пространство состояний или фазовое пространство.
Соответствующая числу степеней свободы совокупность независимых параметров состояния образует пространство состояний или фазовое пространство.
 Пространство состояний является математическим обобщением общеизвестного трехмерного физического пространства и распространяет понятие координаты точки в трехмерном пространстве на более общее понятие фазовой координаты точки.
Пространство состояний является математическим обобщением общеизвестного трехмерного физического пространства и распространяет понятие координаты точки в трехмерном пространстве на более общее понятие фазовой координаты точки.
 Для конечномерных механических систем, движение которых описывается системой уравнений вида (3), пространство состояний представляется как n-мерное координатное пространство, в котором все величины полностью равноправны независимо от их физического смысла и физической размерности.
Для конечномерных механических систем, движение которых описывается системой уравнений вида (3), пространство состояний представляется как n-мерное координатное пространство, в котором все величины полностью равноправны независимо от их физического смысла и физической размерности.
 Подходы к математическому описанию полета
Подходы к математическому описанию полета
 Математическое описание полета как частного вида механического движения основывается на общих законах и теоремах теоретической механики. Для этой цели в общем случае могут быть использованы подходы механики Ньютона, механики Лагранжа и механики Гамильтона.
Математическое описание полета как частного вида механического движения основывается на общих законах и теоремах теоретической механики. Для этой цели в общем случае могут быть использованы подходы механики Ньютона, механики Лагранжа и механики Гамильтона.
 Подход механики Ньютона. Этот подход называют еще силовым подходом. Он опирается на понятие силы и основные теоремы динамики точки и твердого тела, на основе которых записываются исходные векторные уравнения движения ЦМ и вокруг ЦМ.
Подход механики Ньютона. Этот подход называют еще силовым подходом. Он опирается на понятие силы и основные теоремы динамики точки и твердого тела, на основе которых записываются исходные векторные уравнения движения ЦМ и вокруг ЦМ.
 Подход очень нагляден, дает представление о механизме воздействия каждой из сил на движение ЛА, достаточно прост для механических схем ЛА в виде материальной точки или твердого тела, но более сложен в случае составных механических систем, Основная трудность подхода заключается в переходе от векторных уравнений к скалярным, т. е. в проектировании исходных векторных уравнений на оси выбранных СК.
Подход очень нагляден, дает представление о механизме воздействия каждой из сил на движение ЛА, достаточно прост для механических схем ЛА в виде материальной точки или твердого тела, но более сложен в случае составных механических систем, Основная трудность подхода заключается в переходе от векторных уравнений к скалярным, т. е. в проектировании исходных векторных уравнений на оси выбранных СК.
 Подход применим как для свободных систем, так и для систем со связями. В последнем случае связи заменяются реакциями связей, т. е. в число действующих сил добавляются силы реакции связей.
Подход применим как для свободных систем, так и для систем со связями. В последнем случае связи заменяются реакциями связей, т. е. в число действующих сил добавляются силы реакции связей.
 Подход механики Лагранжа. Этот подход называют энергетическим, так как в его основе лежат понятие энергии и дифференциальные уравнения Лагранжа П рода. Формализм Лагранжа позволяет получить сразу скалярные уравнения, т. е. исключает операцию проектирования векторных уравнений.
Подход механики Лагранжа. Этот подход называют энергетическим, так как в его основе лежат понятие энергии и дифференциальные уравнения Лагранжа П рода. Формализм Лагранжа позволяет получить сразу скалярные уравнения, т. е. исключает операцию проектирования векторных уравнений.
 Сущность подхода заключается в записи дифференциальных уравнений Лагранжа II рода для обобщенных координат и обобщенных скоростей в следующей последовательности: где Т - кинетическая энергия; - обобщенные координаты и обобщенные скорости; обобщенные силы; N - число степеней свободы.
Сущность подхода заключается в записи дифференциальных уравнений Лагранжа II рода для обобщенных координат и обобщенных скоростей в следующей последовательности: где Т - кинетическая энергия; - обобщенные координаты и обобщенные скорости; обобщенные силы; N - число степеней свободы.
 Основные трудности этого подхода состоят в определении обобщенных сил. Подход удобен для записи уравнений движения составных механических систем.
Основные трудности этого подхода состоят в определении обобщенных сил. Подход удобен для записи уравнений движения составных механических систем.
 Подход механики Гамильтона. Этот подход основан на использовании канонических уравнений Гамильтона для обобщенных фазовых координат и обобщенных импульсов : где - гамильтониан; - функция Лагранжа; Т - кинетическая энергия системы; U - потенциальная энергия системы.
Подход механики Гамильтона. Этот подход основан на использовании канонических уравнений Гамильтона для обобщенных фазовых координат и обобщенных импульсов : где - гамильтониан; - функция Лагранжа; Т - кинетическая энергия системы; U - потенциальная энергия системы.
 В итоге применения формализма Гамильтона получаются сразу скалярные уравнения в нормальной форме.
В итоге применения формализма Гамильтона получаются сразу скалярные уравнения в нормальной форме.
 Получаемая в результате использования этих подходов механики система скалярных уравнений определяет механическое движение самого ЛА как механического объекта без учета работы СУ.
Получаемая в результате использования этих подходов механики система скалярных уравнений определяет механическое движение самого ЛА как механического объекта без учета работы СУ.
 Для моделирования управляемого движения ЛА, снабженного СУ, полученную систему уравнений необходимо дополнить уравнениями работы системы управления. Система управления определяют управляющие воздействия в виде управляющих сил и моментов, с помощью которых и осуществляется управление полетом.
Для моделирования управляемого движения ЛА, снабженного СУ, полученную систему уравнений необходимо дополнить уравнениями работы системы управления. Система управления определяют управляющие воздействия в виде управляющих сил и моментов, с помощью которых и осуществляется управление полетом.
 Для записи уравнений работы системы управления используются методы теории автоматического управления.
Для записи уравнений работы системы управления используются методы теории автоматического управления.






