 Тема 2: Отношения
Тема 2: Отношения
 • Отношения – один из способов задания взаимосвязей между элементами множества • Унарные (одноместные) отношения отражают наличие признака R у элемента множества M. Все элементы a из множества M, которые отличаются признаком R, образуют подмножество в M, называемое унарным отношением R, т. е. a ∈ R и R ⊆ M. • Бинарные (двухместные) отношения определяют взаимосвязи, которыми характеризуются пары элементов множества M. Все пары (a, b) элементов из M, между которыми имеет место отношение R, образуют подмножество пар из множества всех возможных пар элементов M⨉M=M², называемое бинарным отношением R, т. е. (a, b)∈R и R⊆M⨉M.
• Отношения – один из способов задания взаимосвязей между элементами множества • Унарные (одноместные) отношения отражают наличие признака R у элемента множества M. Все элементы a из множества M, которые отличаются признаком R, образуют подмножество в M, называемое унарным отношением R, т. е. a ∈ R и R ⊆ M. • Бинарные (двухместные) отношения определяют взаимосвязи, которыми характеризуются пары элементов множества M. Все пары (a, b) элементов из M, между которыми имеет место отношение R, образуют подмножество пар из множества всех возможных пар элементов M⨉M=M², называемое бинарным отношением R, т. е. (a, b)∈R и R⊆M⨉M.
 • n-местное отношение – подмножество R прямого произведения n множеств: R⊆M 1⨉…⨉Mn. Говорят, что элементы a 1, a 2, …, an (a 1∈M 1; a 2∈M 2; …; an∈Mn) находятся в отношении R, если (a 1, a 2, …, an)∈R. Если n-местное отношение R задано на множестве M своих элементов, т. е. M 1=M 2=…=Mn, то R⊆Mn.
• n-местное отношение – подмножество R прямого произведения n множеств: R⊆M 1⨉…⨉Mn. Говорят, что элементы a 1, a 2, …, an (a 1∈M 1; a 2∈M 2; …; an∈Mn) находятся в отношении R, если (a 1, a 2, …, an)∈R. Если n-местное отношение R задано на множестве M своих элементов, т. е. M 1=M 2=…=Mn, то R⊆Mn.
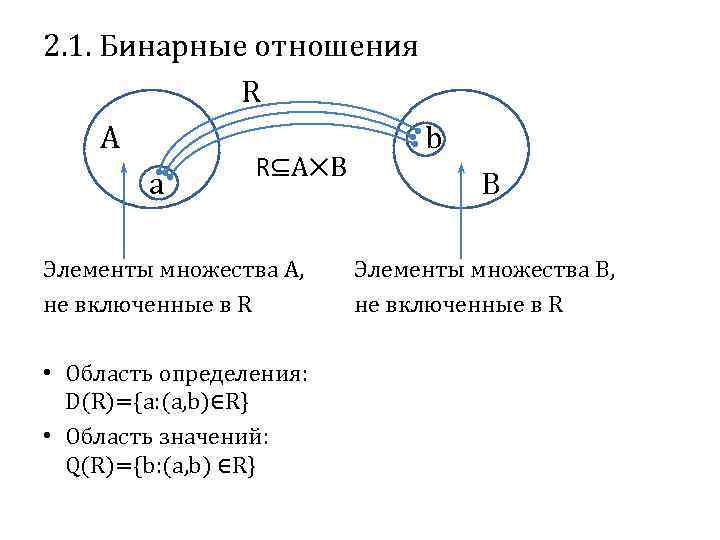 2. 1. Бинарные отношения R A b R⊆A⨉B a Элементы множества A, не включенные в R • Область определения: D(R)={a: (a, b)∈R} • Область значений: Q(R)={b: (a, b) ∈R} B Элементы множества B, не включенные в R
2. 1. Бинарные отношения R A b R⊆A⨉B a Элементы множества A, не включенные в R • Область определения: D(R)={a: (a, b)∈R} • Область значений: Q(R)={b: (a, b) ∈R} B Элементы множества B, не включенные в R
 • Отношения задаются: 1. Списком (перечислением) пар. R={(a, b), (a, c), (b, d)} 2. Матрицей. M={a 1, a 2, …, an} R⊆M⨉M Пример 1. Пусть M={1, 2, 3, 4, 5, 6, 7}. Задать в явном виде (списком) и матрицей отношение R⊆M⨉M, если R означает – «быть строго меньше» .
• Отношения задаются: 1. Списком (перечислением) пар. R={(a, b), (a, c), (b, d)} 2. Матрицей. M={a 1, a 2, …, an} R⊆M⨉M Пример 1. Пусть M={1, 2, 3, 4, 5, 6, 7}. Задать в явном виде (списком) и матрицей отношение R⊆M⨉M, если R означает – «быть строго меньше» .
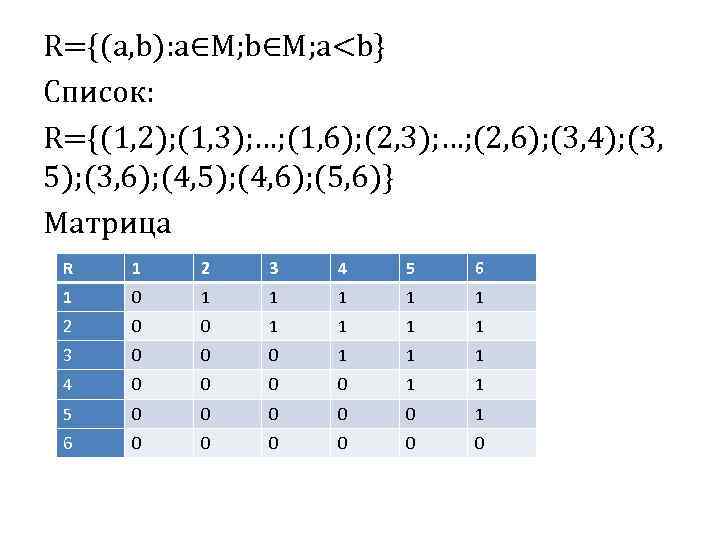 R={(a, b): a∈M; b∈M; a
R={(a, b): a∈M; b∈M; a
 2. 2. Свойства бинарных отношений R – отношение, M – множество R⊆M⨉M 1. 2. 3. 4. R – рефлексивно, если ∀a∈R a R – антирефлексивно, если ∄a∈R : a R – симметрично, если из a R b следует b R a R – антисимметрично, если ∄(a, b) : a≠b для которой из a R b следует b R a 5. R – транзитивно, если из a R b и b R c следует a R c
2. 2. Свойства бинарных отношений R – отношение, M – множество R⊆M⨉M 1. 2. 3. 4. R – рефлексивно, если ∀a∈R a R – антирефлексивно, если ∄a∈R : a R – симметрично, если из a R b следует b R a R – антисимметрично, если ∄(a, b) : a≠b для которой из a R b следует b R a 5. R – транзитивно, если из a R b и b R c следует a R c
 Пример 1. Какими признаками характеризуется матрица отношения R, если R обладает свойствами 1 -5. (Не одновременно!) 1. Главная диагональ матрицы рефлексивного отношения состоит из единиц. 2. Главная диагональ матрицы антирефлексивного отношения состоит из нулей. 3. Матрица симметричного отношения симметрична относительно главной диагонали. 4. В матрице антисимметричного отношения отсутствуют единицы, симметричные относительно главной диагонали.
Пример 1. Какими признаками характеризуется матрица отношения R, если R обладает свойствами 1 -5. (Не одновременно!) 1. Главная диагональ матрицы рефлексивного отношения состоит из единиц. 2. Главная диагональ матрицы антирефлексивного отношения состоит из нулей. 3. Матрица симметричного отношения симметрична относительно главной диагонали. 4. В матрице антисимметричного отношения отсутствуют единицы, симметричные относительно главной диагонали.
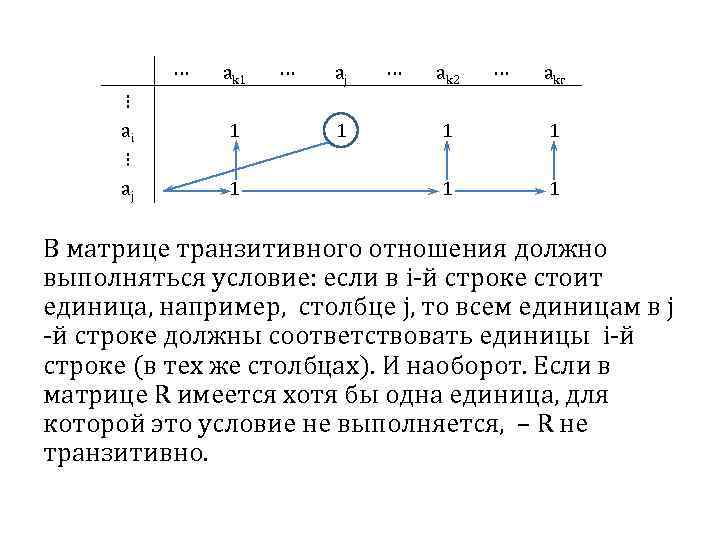 ⋯ ⋮ ai ⋮ aj ak 1 1 1 ⋯ aj 1 ⋯ ak 2 ⋯ akr 1 1 В матрице транзитивного отношения должно выполняться условие: если в i-й строке стоит единица, например, столбце j, то всем единицам в j -й строке должны соответствовать единицы i-й строке (в тех же столбцах). И наоборот. Если в матрице R имеется хотя бы одна единица, для которой это условие не выполняется, – R не транзитивно.
⋯ ⋮ ai ⋮ aj ak 1 1 1 ⋯ aj 1 ⋯ ak 2 ⋯ akr 1 1 В матрице транзитивного отношения должно выполняться условие: если в i-й строке стоит единица, например, столбце j, то всем единицам в j -й строке должны соответствовать единицы i-й строке (в тех же столбцах). И наоборот. Если в матрице R имеется хотя бы одна единица, для которой это условие не выполняется, – R не транзитивно.
 2. 3. Эквивалентность и порядок Отношением эквивалентности называется бинарное отношение на множестве, если оно рефлексивно, симметрично, транзитивно. • разбиение • классы эквивалентности • индекс разбиения Отношение нестрогого порядка – рефлексивно, антисимметрично, транзитивно.
2. 3. Эквивалентность и порядок Отношением эквивалентности называется бинарное отношение на множестве, если оно рефлексивно, симметрично, транзитивно. • разбиение • классы эквивалентности • индекс разбиения Отношение нестрогого порядка – рефлексивно, антисимметрично, транзитивно.
 Отношение нестрогого порядка – антирефлексивно, антисимметрично, транзитивно. Элементы a, b ∈ M сравнимы по отношению порядка R на M, если выполняется a R b или b R a. • полностью упорядоченное множество • частично упорядоченное множество
Отношение нестрогого порядка – антирефлексивно, антисимметрично, транзитивно. Элементы a, b ∈ M сравнимы по отношению порядка R на M, если выполняется a R b или b R a. • полностью упорядоченное множество • частично упорядоченное множество
 2. 4. Операции над бинарными отношениями 1. Объединение R 1∪R 2={(a, b): (a, b)∈R 1 или (a, b)∈R 2} 2. Пересечение R 1∩R 2={(a, b): (a, b)∈R 1 и (a, b)∈R 2} 3. Разность R 1R 2={(a, b): (a, b)∈R 1 и (a, b)∉R 2} 4. Дополнение R=UR, где U=M 1⨉M 2 (или U=M 2)
2. 4. Операции над бинарными отношениями 1. Объединение R 1∪R 2={(a, b): (a, b)∈R 1 или (a, b)∈R 2} 2. Пересечение R 1∩R 2={(a, b): (a, b)∈R 1 и (a, b)∈R 2} 3. Разность R 1R 2={(a, b): (a, b)∈R 1 и (a, b)∉R 2} 4. Дополнение R=UR, где U=M 1⨉M 2 (или U=M 2)
 5. Обратное отношение R-1: R-1={(a, b): (b, a)∈R} /R – быть младше R-1 – быть старше/ 6. Композиция отношений R 1∘R 2: (a, b)∈R 1∘R 2, если ∃c: (a, c)∈R 1 и (c, b)∈R 2
5. Обратное отношение R-1: R-1={(a, b): (b, a)∈R} /R – быть младше R-1 – быть старше/ 6. Композиция отношений R 1∘R 2: (a, b)∈R 1∘R 2, если ∃c: (a, c)∈R 1 и (c, b)∈R 2


