Тема 2 Линейные дискретные преобразования изображений Литература для

Тема 2. Линейные дискретные преобразования изображений Литература для углубленного изучения: 1. Гоноровский И. С. Радиотехнические цепи и сигналы 2. Баскаков С. И. Радиотехнические цепи и сигналы 3. Бернюков А. К. Дискретная и цифровая обработка информации 4. Оппенгейм А. , Шафер Р. Цифровая обработка сигналов

План 1. Линейные дискретные преобразования изображений 2. 2 -мерное Дискретное преобразование Фурье (ДПФ) 3. Свойства ДПФ

1. Линейные дискретные преобразования изображений

Области применения глобальных двумерных ортогональных преобразований для обработки изображений • для выделения характеристик признаков изображения; • для кодирования изображений, когда ширина спектра уменьшается за счет отбрасывания или грубого квантования малых по величине коэффициентов преобразования; • для сокращения размерности при выполнении вычислений.

Пример ДОП • • • Фурье, синусные, косинусные, вейвлет-преобразования, а также преобразования Карунена. Лоева, Уолша, Хаара и Адамара.

• ДПП – перенос исходного изображения в частотную область • ДПО – восстановление исходного изображения по спектру • Фильтрация в частотной области – умножение Фурье-образа изображения на ЧХ фильтра.

Основные процедуры глобальной обработки изображений, осуществляемые как в пространственной, так и в пространственно-частотной области

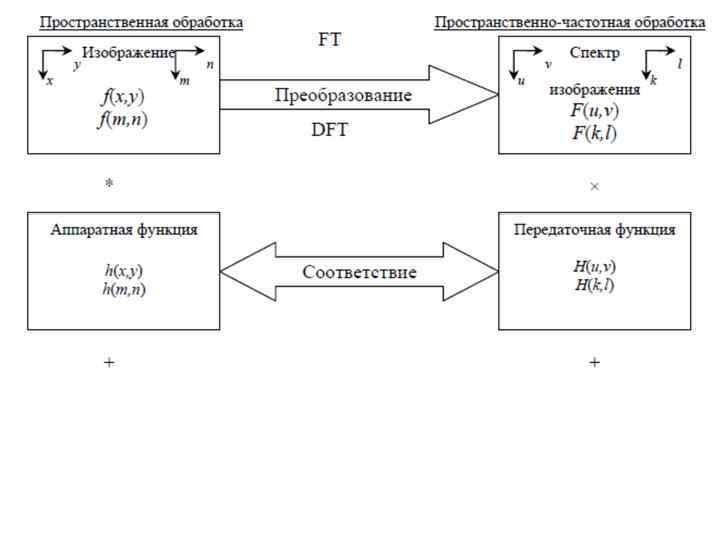
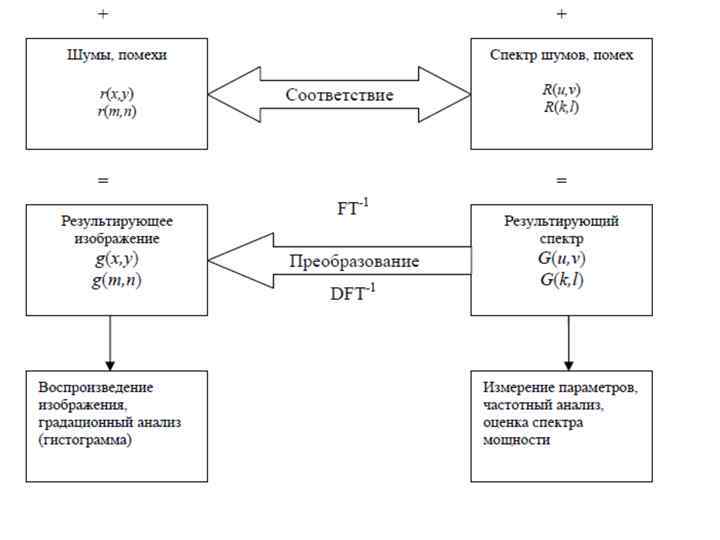
Применение дискретных ортогональных преобразований Хартли, Хаара, Уолша-Адамара: • альтернатива ДОП Фурье для решения задач: – – – – – предварительной обработки изображений, устранения шумов и помех, оптимальной винеровской фильтрации, повышения качества визуального восприятия изображений, выделения границ объектов и их сегментации в целях классификации и распознавания образов, анализа спектров изображений, вычисления дискретной свертки, корреляционной функции и других операциях над спектрами.

2. 2 -мерное Дискретное преобразование Фурье (ДПФ)

• Условие для БПФ nxm n=m=2 p где p N Пусть JJ – матрица преобразования размера J J: • ДПФ

• Матрица обратного преобразования • Инверсия преобразования Фурье

• Ядро дискретного преобразования

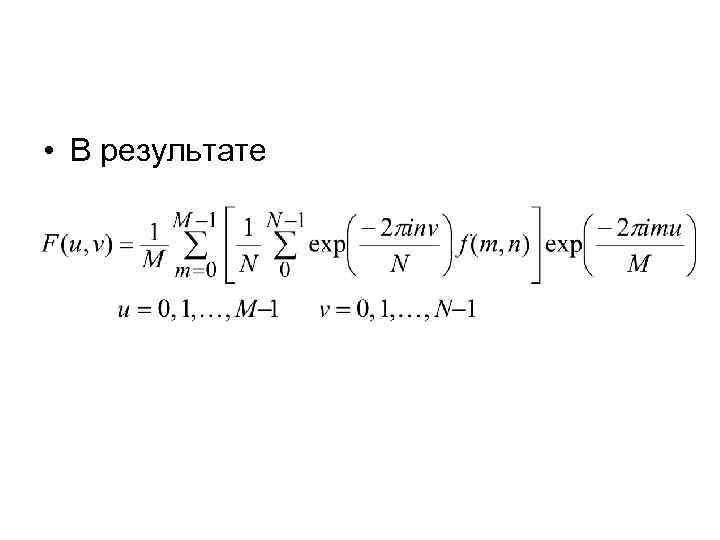
• В результате

• Образ Фурье действительной функции – комплексная функция |F(u, v)| - частотный спектр изображения f(m, n)

• фазовый спектр • спектр мощности

изображение частотный спектр как функция интенсивности

• Пусть изображение f(x, y) (2 -мерный сигнал), имеет размер 128,

• Амплитуда спектра - четная функция М(u) = М (-u) • Фаза спектра - нечетная функция -P(u) = P(-u)

Пример 2 -мерного ступенчатого сигнала

Амплитуда спектра изображения f(x, y)

ДПФ одномерного сигнала длины 128

Одномерный профиль ДПФ по горизонтальной линии y = 64 Одномерный профиль амплитуды спектра Одномерный профиль фазы спектра

2 -мерное ДПФ F(u, v) может быть получено: 1. С помощью 1 -мерного ДПФ от каждой строки изображения f(x, y), F(u, y), 2. С помощью 1 -мерного ДПФ от каждого столбца F(u, y)

исходное изображение f(x, y) спектр строки F(u, y) спектр изображения F(u, v)

3. Свойства ДПФ

• Вращение. Поворот f(x, y) на угол также приводит к повороту спектра ДПФ F(u, v) на угол . исходное изображение f(x, y); спектр исходного изображения F(u, v) повернутое изображение f(x, y); спектр повернутого изображения F(u, v)

Линейная комбинация. • ДПФ - линейный оператор, поэтому верно следующее: k 1 f(x, y) + k 2 g(x, y) k 1 F(u, v) + k 2 G(u, v)

Изображение A Изображение B 0. 25 A + 0. 75 B Спектр A Спектр B 0. 25 A + 0. 75 B

• Трансляция. При трансляции первоначального изображения на (x 0, y 0), амплитудный спектр ДПФ смещенного изображения будет тем же самым, что и у первоначального изображения, но изменяется фаза:

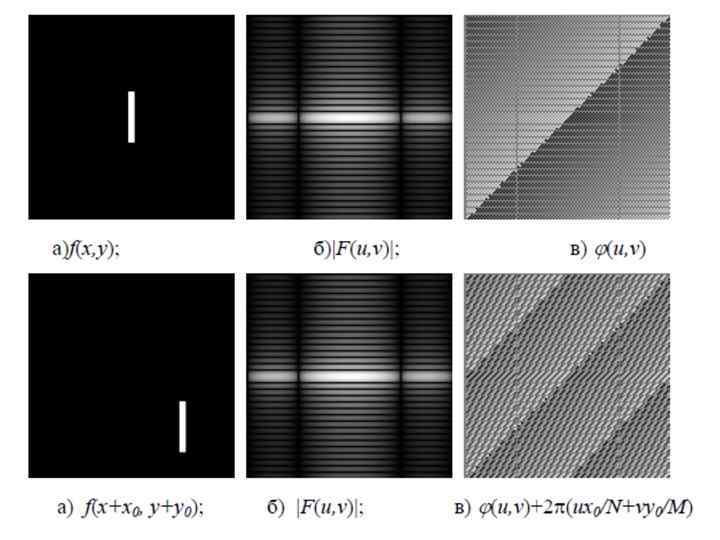
• При смещении спектра ДПФ на (u 0, v 0) • Это свойство используется при отображении оптических Фурье-спектров. Смещение на (N/2, M/2) в F(u, v) эквивалентно умножению f (x, y) на (-1) (x + y).