Тема 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 1. 3. Методы

Тема 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 1. 3. Методы линейного программирования

1. 3. 1. Алгебраический симплексный метод o Алгебраический симплексный метод применяется для решения задач линейного программирования, ограничения в которых представлены в виде неравенств смысла « » . Симплексный метод – это итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по угловым точкам области возможных решений до тех пор, пока не достигнет оптимального значения, в частности по угловым точкам многоугольника решений, полученного геометрическим методом. Для унификации процедуры ручного счета при решении задач ЛП с использованием симплекс-метода применяются симплекс-таблицы.

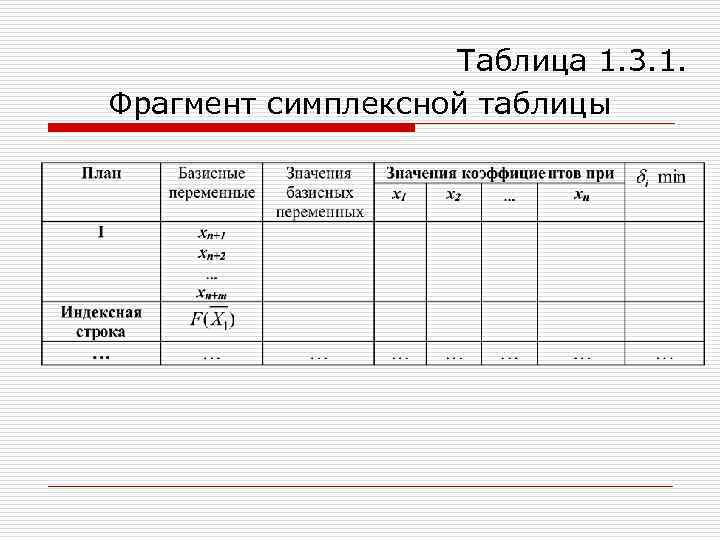
Алгоритм решения задачи линейного программирования алгебраическим симплексным методом на основе заполнения симплексной таблицы 1. Составление первого опорного плана. Система ограничений задачи, решаемой симплексным методом, задана в виде неравенств смысла « » , правые части которых . Перейдем от системы неравенств к системе уравнений путем добавления неотрицательных дополнительных переменных к левой части ограничений-неравенств. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными. где ‑ основные, свободные переменные , ‑ дополнительные, базисные переменные . Приравняем основные переменные задачи к нулю: , и получим первый опорный план: Занесем полученный опорный план в симплексную таблицу, которая состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами целевой функции, взятыми с противоположными знаками (табл. 1. 3. 1).

Таблица 1. 3. 1. Фрагмент симплексной таблицы

2. Проверка плана на оптимальность. Если все коэффициенты индексной строки симплексной таблицы неотрицательны при решении задачи на максимум или отрицательны при решении задачи на минимум, то план является оптимальным. В противном случае план не является оптимальным и его можно улучшить. В таком случае переходим к третьему этапу. 3. Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине (при решении задачи на максимум) или из положительных коэффициентов выбираем наибольший (при решении задачи на минимум), что и определяет ведущий столбец. Он показывает, какая переменная на следующей итерации перейдет из свободных в базисные. Затем элементы столбца свободных членов на элементы того же знака ведущего столбца. Результаты заносим в отдельный столбец , элементы которого будут всегда положительные. Строка симплексной таблицы, соответствующая минимальному значению является ведущей. Она определяет переменную, которая на следующей итерации выйдет из базиса и станет свободной. Элемент симплексной таблицы, находящийся на пересечении ведущих столбца и строки, называется разрешающим (РЭ).

4. Построение нового опорного плана. Переход к новому опорному плану осуществляется в результате пересчета симплексной таблицы методом Жордана – Гаусса. Сначала замени переменные в базисе. Затем разделим элементы ведущей строки предыдущего опорного плана на разрешающий элемент, и результаты деления занесем в строку следующего опорного плана. В результате деления на месте разрешающего элемента в следующем опорном плане будет единица, а в остальных клетках данного столбца записываем нули. Остальные новые элементы нового плана находим по правилу прямоугольника: где СТЭ – элемент старого плана, РЭ – разрешающий элемент, А и В – элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Далее возвращаемся ко второму этапу алгоритма.

Примечание 1. (Задача не имеет решения). Если в ведущем столбце все коэффициенты , то целевая функция не ограничена на множестве допустимых планов, т. е. и задача не имеет решения.

Примечание 2. (Задача имеет множество решений ). o Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедший в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. o Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. o В результате будет получен второй оптимальный план с другим набором базисных переменных.

Примечание 3. (Вырожденность плана). o Если в столбце симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных переменных станут равными нулю). o Вырожденные планы могут привести к зацикливанию, т. е. многократному повторению процесса вычислений, не позволяющему получить оптимальный план. o С целью исключения этого для выбора ведущей строки используют метод Креко, который заключается в следующем. Элементы строк, имеющие одинаковые наименьшие значения делятся на предполагаемые разрешающие элементы, а результаты заносятся в дополнительные строки. За ведущую строку выбирается та, в которой встретится наименьшее частное при чтении таблицы слева направо по столбцам, включая нуль и отрицательные значения.

1. 3. 2. Метод искусственного базиса (М-метод) Симплексный метод решения задач базируется на введении дополнительных переменных, позволяющих образовать единичную матрицу, в которую не допускаются отрицательные и другие числа, кроме нуля и единицы. Наличие единичной матрицы является необходимым условием при решении задач симплексным методом. Если же ограничения задачи заданы в виде неравенств вида или уравнений: то невозможно сразу получить начальное базисное решение, если матрица, составленная из коэффициентов при неизвестных системы ограничений, не позволяет образовать единичную матрицу.

Причем уравнения отражают жесткие условия ограничений по ресурсам, не допускающих никаких отклонений. Для соблюдения равенств вводятся искусственные переменные yi, равные нулю. Векторы искусственных переменных образуют необходимую для решения единичную матрицу. Такой базис называется искусственным, а метод решения называется методом искусственного базиса. Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.

За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый “штраф” величиной М, очень большое положительное число, которое обычно не задается (М ). Для постановки задачи на минимум целевую функцию записывают в виде: Для решения задачи на максимум целевую функцию следует записать иначе:

o Далее задача решается симплексным методом до тех пор, пока не получатся в индексной строке положительные числа при решении задачи на максимум или отрицательные числа при решении задачи на минимум. o Преобразование разнородных ограничений, представляющих собой смесь уравнений и неравенств разного вида, заключается в образовании базиса решения путем одновременного введения свободных и искусственных переменных, что придает симплексному методу большую гибкость.

1. 3. 3. Графический метод решения задач ЛП Данный способ применяется: o если математическая модель задачи представлена в виде неравенств ( ) и содержит не более двух переменных; o если задача задана в канонической форме (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2, т. е. n - m = 2. o Данный метод основан на геометрическом представлении допустимых решений и ЦФ задачи.

o Каждое из неравенств задачи ЛП определяет на координатной плоскости некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. o Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). o ОДР всегда представляет собой выпуклую фигуру, т. е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. o ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. o В случае несовместности системы ограничений задачи ОДР является пустым множеством.

Решение задачи линейного программирования графическим методом включает следующие этапы: 1. На плоскости строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств. 2. Находят полуплоскости, определяемые каждым из ограничений задачи. 3. Строят многоугольник решений. 4. Строят вектор-градиент который указывает направление возрастания целевой функции.

5. Строят начальную прямую целевой функции перпендикулярную вектору градиенту и затем передвигают ее в направлении вектора до крайней угловой точки многоугольника решений (при решении задачи на максимум) или в противоположном направлении (при решении задачи на минимум). В результате находят: -точку, в которой целевая функция принимает максимальное (минимальное) значение, -либо множество точек с одинаковым максимальным (минимальным) значением целевой функции, если начальная прямая сливается с одной из сторон многоугольника решений, -либо устанавливается неограниченность сверху (снизу) целевой функции на множестве планов, т. е.

6. Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке. Примечание: Если начальная прямая сливается с одной из сторон многоугольника решений, то множество оптимальных решений записывают как линейную выпуклую комбинацию углов точек отрезка по формуле: где , А и В начальная и конечная точка отрезка. Подставляя любые значения от 0 до 1, получают координаты множество точек отрезка АВ, в каждой из которых целевая функция принимает максимальное (минимальное) значение.

o Графический метод решения задач ЛП обладает рядом достоинств: прост, нагляден, позволяет быстро и легко получить ответ. o Однако при реализации данного метода возможны «технические» погрешности, которые неизбежно возникают приближенном построении графиков. o Второй недостаток графического метода заключается в том, что многие величины, имеющие четкий экономический смысл (такие, как остатки ресурсов производства, избыток питательных веществ и т. п. ), не выявляются при геометрическом решении задач. o Но самое главное – графический метод неприемлем для решения практических задач, т. к. его можно применить лишь в том случае, когда число переменных в стандартной задаче равно двум.