ТЕМА 2 ЭКОНОМИЧЕСКИЙ РОСТ 1 Характер экономического

ТЕМА 2: ЭКОНОМИЧЕСКИЙ РОСТ

1. Характер экономического роста предыдущих лет. Исследования экономического роста. 2. Взаимодействие между ВВП, капиталом и нормой сбережений. 3. Технический прогресс и темпы экономического роста. Детерминанты технического прогресса 4. Фундаментальные факторы, определяющие уровень жизни в долгосрочном периоде. Государственная политика повышения уровня жизни в долгосрочном периоде: политика, воздействующая на уровень сбережений и политика, воздействующая на рост уровня производительности.

1. Характер экономического роста предыдущих лет.

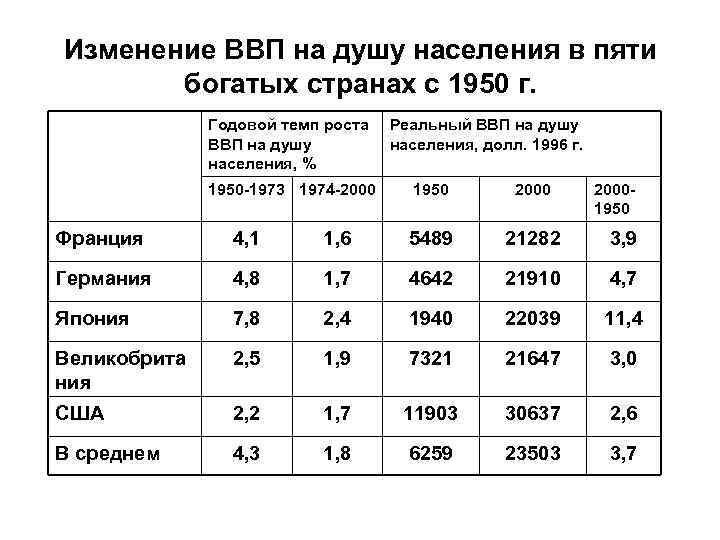Изменение ВВП на душу населения в пяти богатых странах с 1950 г. Годовой темп роста ВВП на душу населения, % 1950 -1973 1974 -2000 Реальный ВВП на душу населения, долл. 1996 г. 1950 20001950 Франция 4, 1 1, 6 5489 21282 3, 9 Германия 4, 8 1, 7 4642 21910 4, 7 Япония 7, 8 2, 4 1940 22039 11, 4 Великобрита ния 2, 5 1, 9 7321 21647 3, 0 США 2, 2 1, 7 11903 30637 2, 6 В среднем 4, 3 1, 8 6259 23503 3, 7

Выводы из таблицы: 1. Уровень жизни вырос многократно. 2. Темпы роста ВВП на душу населения снизились с середины 1970 -х гг. 3. Уровни ВВП на душу населения между этими пятью странами конвергировали (стали ближе).

МОДЕЛЬ Р. СОЛОУ

РОБЕРТ СОЛОУ Born August 23, 1924 New York Field Economics US USA Institution Alma Mater Doctoral Advisor MIT Harvard University Wassily Leontief Doctoral Students George Akerlof Ben Bernanke Joseph Stiglitz Known for Neo-classical growth model Notable Prizes John Bates Clark Medal (1961) Nobel Prize in Economics (1987)

Допущения в модели Солоу: • труд и капитал являются полностью взаимозаменяемыми (субститутами); • постоянная отдача от масштаба производства; • предельная производительность капитала убывает; • постоянная норма выбытия капитала; • инвестиционные лаги отсутствуют.

Условие равновесия экономической системы равенство совокупного спроса и совокупного предложения. Это предполагает анализ факторов, определяющих величины совокупного спроса и совокупного предложения.

Совокупное предложение в модели Солоу: • описывается агрегатной производственной функцией (типа Кобба-Дугласа) с постоянной отдачей от масштаба производства: Y = F(K, L), где Y – объем выпуска, K, L – капитал и труд.

• Вследствие допущения постоянной отдачи от масштаба производства для любого положительного числа z верно: z. Y = F(z. K, z. L)

• Если примем, что z = 1/L, то Y/L = F (K/L, 1). • Это уравнение показывает, что объем выпуска в расчете на одного работника (Y/L) является функцией капитала на одного работника (K/L).

• k = K/L – капиталовооруженность, • у = Y/L – производительность труда. • Соответственно, предыдущую функцию можно представить в форме взаимосвязи между производительностью и капиталовооруженностью: у = f(k)

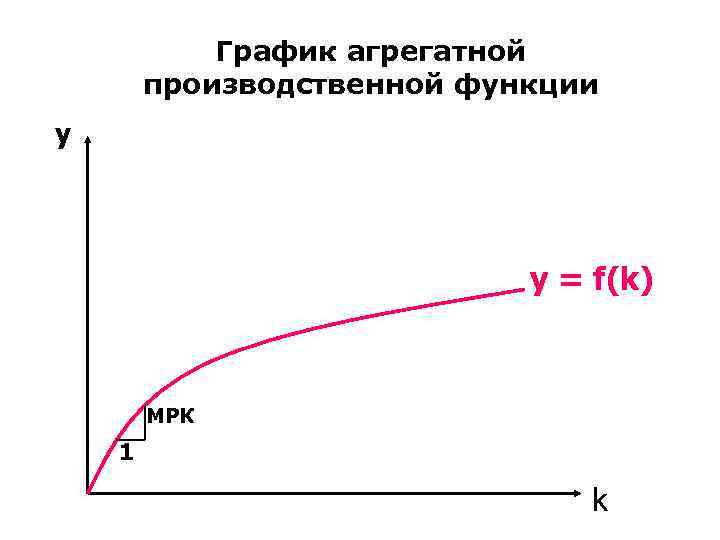График агрегатной производственной функции y у = f(k) МРК 1 k

Описание графика агрегатной производственной функции: • График производственной функции показывает, как капиталовооруженность k определяет размер выпуска продукции на одного работника: у = f(k). • Тангенс угла наклона графика производственной функции равен предельной производительности капитала: если k увеличивается на одну единицу, то y возрастает на MPK единиц. По мере возрастания k кривая производственной функции становится более пологой, что свидетельствует о снижении предельной производительности.

2. Взаимодействие между ВВП, капиталом и нормой сбережений

Спрос в модели Солоу: • Y = С + I. • Y/L = C/L + I/L. • y = с + i, где с, y, i – потребление, доход, инвестиции на одного работника.

• Предположим, что функция потребления имеет вид: с = (1 – s)y, где s (предельная склонность к сбережению) принимает значения от 0 до 1. • Подставим значение с в функцию y = с + i. Получим y = (1 – s)y + i, или i = sy, или y = i/s. Инвестиции, как и потребление, пропорциональны доходу. Предельная склонность к сбережению показывает, какая часть произведенной продукции направляется на инвестиции.

• При равенстве совокупного спроса и совокупного предложения: • у = f(k), • y = i/s, • i = sf(k).

• Как накопление капитала обеспечивает экономический рост? • Запасы капитала (k) могут изменяться по двум причинам: 1. Инвестиции приводят к росту запасов капитала. 2. Часть капитала изнашивается, т. е. амортизируются. Поэтому для того чтобы понять, как изменяются запасы капитала, необходимо найти факторы, определяющие величину инвестиций и амортизации.

Инвестиции есть функция от капиталовооруженности: i = sf(k). • Чем выше капиталовооруженность, тем выше объем выпуска на одного работника f(k) и больше инвестиции i (k – запасы капитала, i – новый капитал).

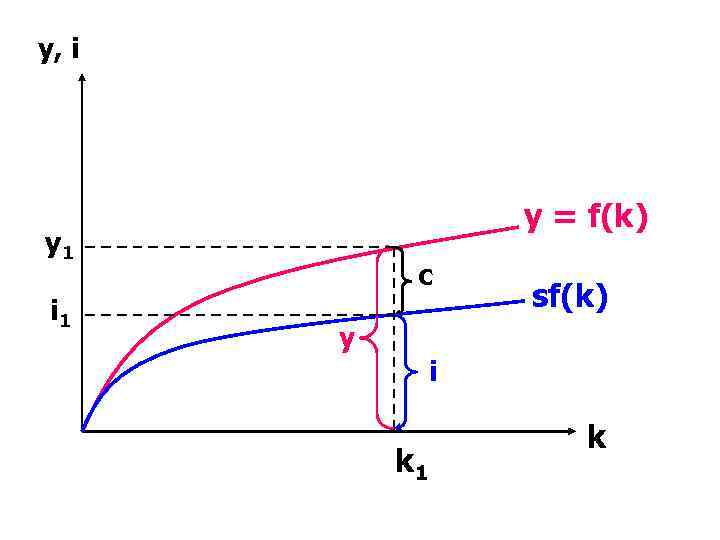y, i у = f(k) y 1 i 1 c sf(k) y i k 1 k

Описание рисунка: • Для любого уровня капиталовооруженности k : • f(k) – объем выпуска на одного работника, • sf(k) – объем инвестиций, • f(k) – sf(k) – объем потребления

• Чтобы учесть амортизацию, предположим, что ежегодно выбывает определенная доля капитала δ, т. е. δ – норма выбытия. • Количество капитала, выбывшего за год, равно δk.

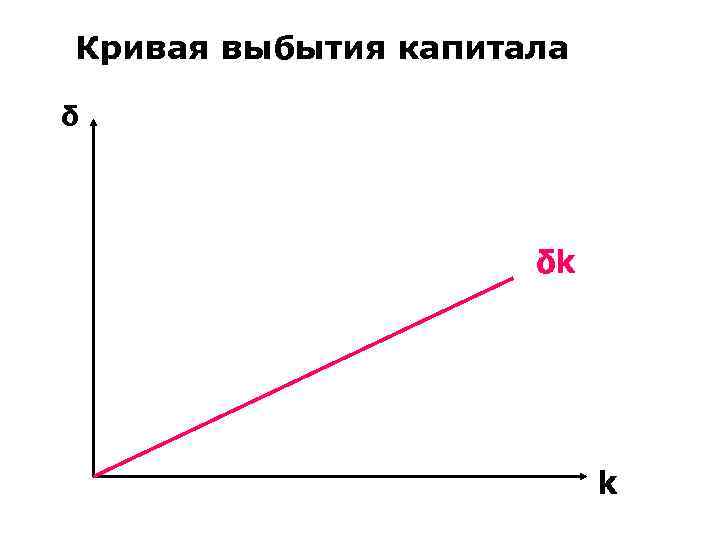Кривая выбытия капитала δ δk k

Устойчивый уровень капиталовооруженности • Существует единственный уровень капиталовооруженности, при котором инвестиции равны выбытию: sf(k) = δk. • Состояние, при котором инвестиции равны выбытию, называется устойчивым уровнем капиталовооруженности k*.

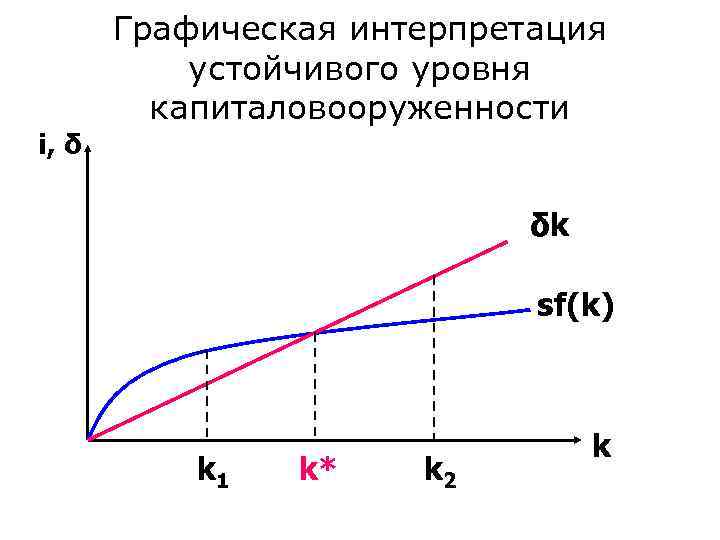Графическая интерпретация устойчивого уровня капиталовооруженности i, δ δk sf(k) k 1 k* k 2 k

Описание рисунка: • Устойчивый уровень капиталовооруженности – это такая капиталовооруженность работников, при которой инвестиции равны выбытию. Он соответствует равновесию экономики в долгосрочном периоде. • Если k 1 < k*, то i > δk, и запасы капитала растут. • Если k 2 > k*, то i < δk, и запасы капитала снижаются.

Что происходит в экономике при изменении предельной склонности к сбережениям (нормы сбережений)? • Рост нормы сбережений s означает, что размер инвестиций при любых уровнях капиталовооруженности станет больше. Поэтому происходит сдвиг вверх кривой функции инвестиций. • В точке прежнего устойчивого равновесия инвестиции теперь будут превышать выбытие. Запасы капитала будут расти, пока экономика не достигнет нового устойчивого состояния.

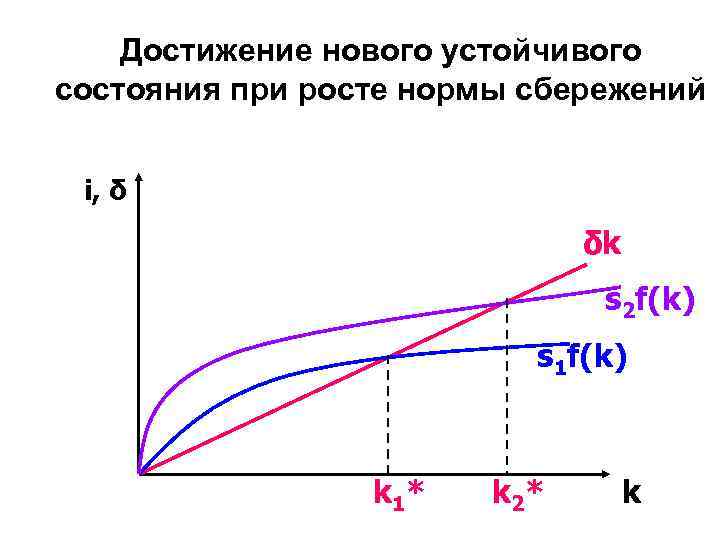Достижение нового устойчивого состояния при росте нормы сбережений i, δ δk s 2 f(k) s 1 f(k) k 1* k 2* k

Основные выводы: Модель Солоу показывает, что норма сбережений является ключевой детерминантой величины устойчивой капиталовооруженности. Если норма сбережений увеличивается, то при прочих равных условиях запас капитала будет расти и соответственно увеличится уровень производства. Более высокие сбережения ведут к более быстрому росту, но это не длится вечно, а до тех пор, пока экономика не достигнет нового устойчивого состояния.

На основе изложенного выше можно рассмотреть взаимосвязь нормы сбережений, капитала и ВВП на душу населения: Взаимодействие между ВВП и капиталом: - воздействие капитала на ВВП - воздействие ВВП на накопление капитала - динамика капитала и ВВП - капитал и ВВП в устойчивом состоянии Последствия альтернативных норм сбережений. - норма сбережений и ВВП - норма сбережений и потребление - воздействие нормы сбережений на ВВП в устойчивом состоянии - динамические эффекты повышения нормы сбережения

Предположим, что какой-то субъект, принимающий экономические решения, может просто выбрать национальную норму сбережений и соответственно определенное устойчивое состояние экономики. Вопрос – какое устойчивое состояние ему следует выбрать? Какие размеры накопления капитала являются оптимальными?

«Золотое правило» Фелпса • Уровень накопления капитала, обеспечивающий устойчивое состояние с наивысшим уровнем потребления, называется золотым уровнем накопления капитала (k**)

• • • y = с + i, с = y – i, i = δk, y = f(k), c* = f(k*) – δk* Устойчивый уровень потребления есть разница между выпуском и выбытием капитала в устойчивом состоянии.

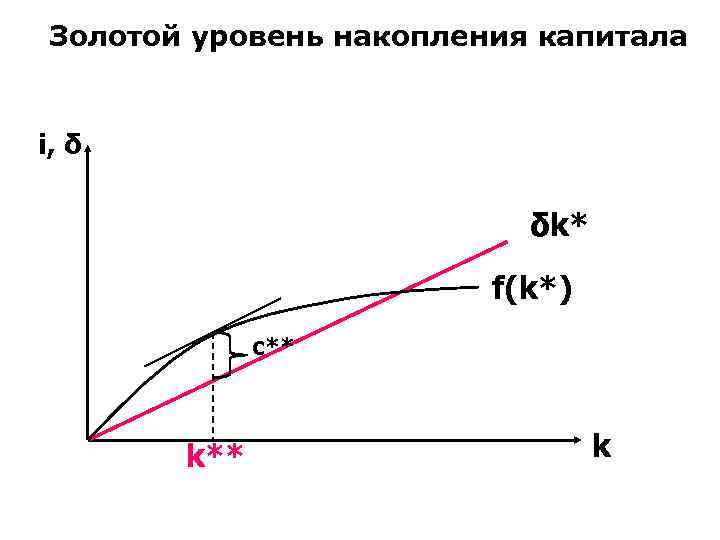Золотой уровень накопления капитала i, δ δk* f(k*) с** k

«Золотое правило » МРК = δ

• Поскольку модель Солоу показывает, что само по себе накопление капитала не может объяснить непрерывный экономический рост, в анализ вводится два источника экономического роста: рост населения и технологический прогресс.

Рост населения как источник экономического роста Предположим, население растет постоянным темпом n. Это влияет на запас капитала в сторону уменьшения: Δk = i – δk – nk, i = sf(k), Δk = sf(k)–δk–nk = sf(k)–(δ+n)k

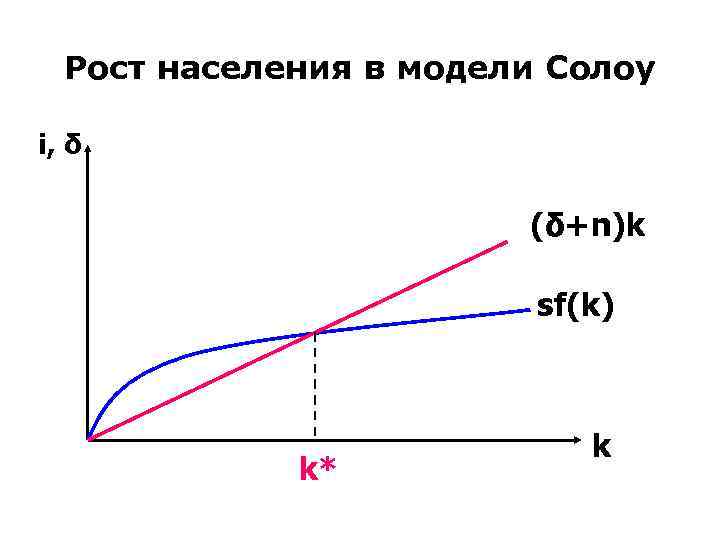Рост населения в модели Солоу i, δ (δ+n)k sf(k) k* k

• Для сохранения устойчивого состояния экономики (когда капитал и выпуск продукции на одного работника остаются неизменными) капитал и объем выпуска должны расти тем же темпом n, каким растет население. • Но в данном случае уровень жизни не изменяется.

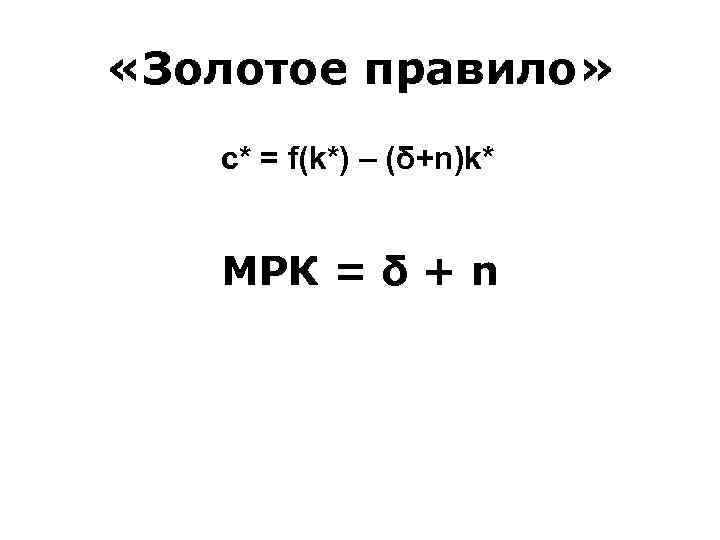«Золотое правило» c* = f(k*) – (δ+n)k* МРК = δ + n

3. Технический прогресс и темпы экономического роста. Детерминанты технического прогресса

Технический прогресс как источник экономического роста • Технический прогресс приводит к росту эффективности труда с постоянным ростом g. Фактически растет количество «эффективных единиц» труда, что аналогично росту населения.

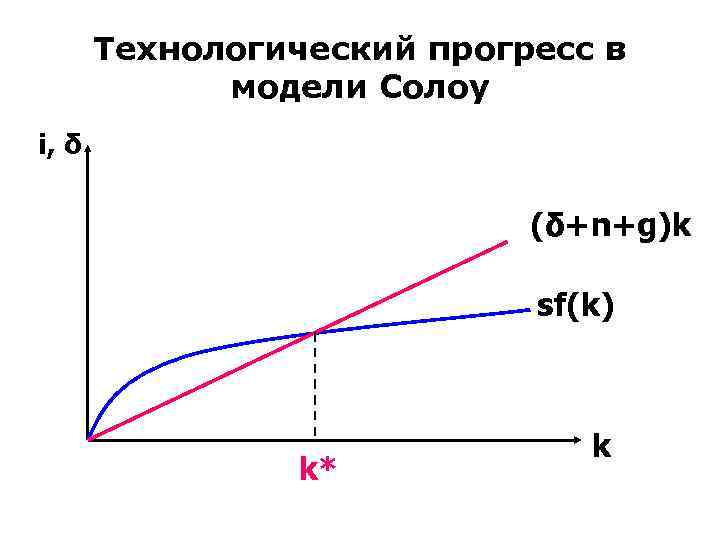Технологический прогреcc в модели Солоу i, δ (δ+n+g)k sf(k) k* k

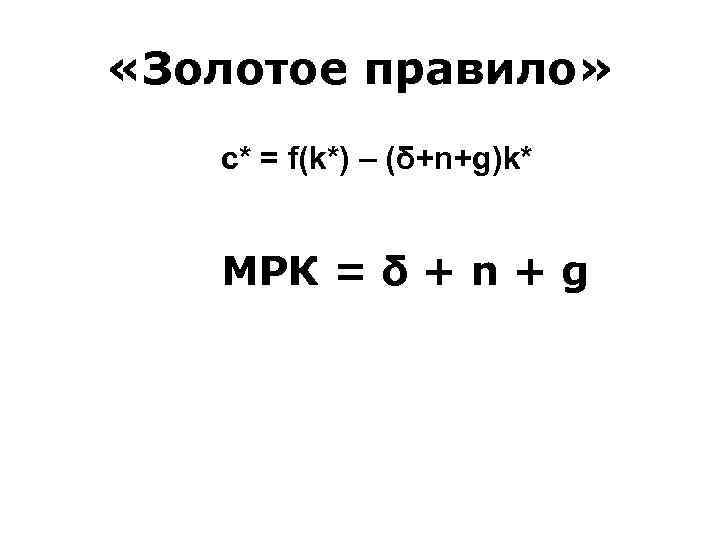«Золотое правило» c* = f(k*) – (δ+n+g)k* МРК = δ + n + g

• Модель Солоу показывает, что только технический прогресс может объяснить непрерывно растущий уровень жизни.

4. Фундаментальные факторы, определяющие уровень жизни в долгосрочном периоде. Государственная политика повышения уровня жизни в долгосрочном периоде: политика, воздействующая на уровень сбережений и политика, воздействующая на рост уровня производительности.

Источниками экономического роста выступают: • сбережения • технологический прогресс

Три вопроса, которые важны с точки зрения экономической политики • Должно ли общество сберегать больше или меньше? • Может ли экономическая политика повлиять на норму сбережений? • Как может экономическая политика влиять на скорость технологического прогресса?

Ответ на первый вопрос: Чтобы оценить общенациональный уровень накопления капитала, необходимо сравнить темп прироста объема выпуска с величиной чистой отдачи от капитала, т. е. (n+g) и (MPK – δ)

Пусть реальный ВВП растет 3% в год, т. е. (n+g) = 0, 03

Рассчитаем предельный продукт капитала, исходя из: 1) запас капитала в 2. 5 раза больше годового ВВП; 2) выбытие капитала составляет 10% ВВП; 3) на долю капитала приходится около 30% общего годового дохода.

первое означает: k = 2, 5 y второе означает: δk = 0, 1 y Поэтому: δ = (δk)/k = (0, 1 y)/(2, 5 y) = 0, 04 т. е. около 4% запаса капитала выбывает каждый год

так как доход на капитал равен его предельному продукту: (МРК × К)/Y = МРК × (К/Y) 0, 30 = МРК × 2, 5 МРК = 0, 30/2, 5 = 0, 12 чистый предельный продукт капитала MPK – δ = 0, 12 – 0, 04 = 0, 08, что больше прироста производства и означает что запасы капитала намного ниже Золотого правила

Вывод: при разработке государственной политики следует стремиться к увеличению нормы сбережений и инвестиций

Пути увеличения национальных сбережений: - увеличение государственных сбережений - увеличение частных сбережений

Поощрение технологического прогресса