Тема 2 3 — 2 4 Дисперсійний

Тема 2. 3. - 2. 4 – Дисперсійний аналіз для незв'язних вибірок. Дисперсійний аналіз для зв'язаних вибірок .

Питання • Основні положення дисперсійного аналізу. • Дисперсійний аналіз для незв'язних вибірок. • Дисперсійний аналіз для зв'язаних вибірок

Література 1. Сидоренко Е. В. Методы математической обработки в психологии. — СПб: Речь, 2001. — 350 с. 2. Гусев А. Н. , Измайлов Ч. А. , Михалевская М. Б. Измерение в психологии: общий психологический практикум. 2 е изд. — Москва: Смысл, 1998. — 286 с. 3. Гмурман В. Е. Теория вероятностей и математическая статистика. — Москва: Высшая школа, 2000. — 479 с.

Дисперсійний аналіз • є методом багатовимірної статистики, який дозволяє здійснювати дослідження впливу якісних факторів і аналізу значущості цього впливу. • При дослідженні психологічних процесів та явищ дисперсійний аналіз може використовуватися для виявлення спільного впливу психологічних факторів, що не піддаються кількісному виміру, на психологічний показник, що досліджується.

• Дисперсійний аналіз це аналіз мінливості ознаки під впливом будь яких контрольованих змінних факторів. У зарубіжній літературі дисперсійний аналіз часто позначається як ANOVA, що перекладається як аналіз варіативності (Analysis of Variance), Автором методу є Р. А. Фішер (Fisher RA, 1918, 1938).

• Завдання дисперсійного аналізу полягає в тому, щоб із загальної варіативності ознаки вичленувати варіативність трояку роду:

• а) варіативність, зумовлену дією кожної з досліджуваних незалежних змінних; б) варіативність, зумовлену взаємодією досліджуваних незалежних змінних; в) випадкову варіативність, зумовлену усіма іншими невідомими змінними.

• Нульова гіпотеза в дисперсійному аналізі буде гласить, що середні величини досліджуваного результативної ознаки у всіх градаціях однакові. Альтернативна гіпотеза буде стверджувати, що середні величини результативної ознаки в різних градаціях досліджуваного фактора різні.

• Справа в тому, що градація увазі ступінь, стадію, рівень розвитку. Говорячи про градаціях фактора, ми явно чи неявно маємо на увазі, що сила його зростає при переході від градації до градації. Між тим, схема дисперсійного аналізу застосовна і в тих випадках, коли градації фактора являють собою номінативну шкалу, тобто відрізняються лише якісно.

• Наприклад, градаціями фактора можуть бути: * Паралельні форми експериментальних завдань; * Колір забарвлення стимулів; * Жанр музичних творів, які супроводжують процес роботи; * Традиційні або спеціально підібрані православні тексти в сеансах аутогенного тренування; * Різні форми захворювання; * Різні експериментатори; * Різні психотерапевти і т. д.

• Дисперсійний аналіз дозволяє нам констатувати зміна ознаки, але при цьому не вказує напрямок цих змін. Нам необхідно спеціально графічно представляти отримані дані по градаціях фактора, щоб отримати наочне уявлення про напрям змін.

• Подібного роду завдання, як ми пам'ятаємо, дозволяють вирішувати непараметричні методи порівняння вибірок або умов вимірювання, а саме критерій Н. Крускала Уолліса і критерій χ 2 r Фрідмана.

Однак це стосується тільки тих завдань, в яких досліджується дія одного чинника, або однієї змінної. Завдання однофакторного дисперсійного аналізу, дійсно, можуть ефективним чином вирішуватися за допомогою непараметричних методів.

• Наприклад, як змінюється час вирішення завдання * За різних умов мотивації випробовуваних (низької, середньої, високої) або * При різних способах пред'явлення завдання (усно, письмово, у вигляді тексту з графіками та ілюстраціями), * В різних умовах роботи з задачею (в самоті, в одній кімнаті з експериментатором і іншими випробуваними) і т. п.

• * У першому випадку змінної, вплив якої досліджується, є мотивація, * У другому ступінь наочності, * В третьому фактор публічності.

• Перевага однофакторного дисперсійного аналізу в порівнянні з непараметричних методів Н Крускала Уолліса і χ 2 r Фрідмана необмеженість у обсягах вибірок. Обмеження дисперсійного аналізу досить умовні. Наприклад, вимога нормальності розподілу ознаки можна обійти принаймні дво ма шляхами: при занадто скошеному, островершінном або плосковершінних розподілі можна, по-перше, нормалізувати дані, а по-друге. . . просто взагалі з цього приводу "не хвилюватися", як радять, наприклад, А. К. Kurtz і ST Мауо (1979, р. 417).

Однофакторний дисперсійний аналіз для незв'язаних вибірок

Призначення методу • Метод однофакторного дисперсійного аналізу застосовується в тих випадках, коли досліджуються зміни результативної ознаки під впливом зміни умов або градацій якого фактора. У даному варіанті методу впливу кожної з градацій фактора піддаються різні вибірки випробуваних. Градацій фактора повинно бути не менше трьох.

Опис методу • Роботу починаємо з того, що представляємо отримані дані у вигляді стовпців індивідуальних значень. Кожен із стовпців відповідає тому або іншому з досліджуваних умов.

• Після цього нам потрібно підсумувати індивідуальні значення по стовпцях і суми звести в квадрат. Суть методу полягає в тому, щоб зіставити суму цих зведених в квадрат сум з сумою квадратів усіх значень, отриманих у всьому експерименті.

Гіпотези H 0: Відмінності між градаціями фактора (різними умовами) є не більш вираженими, ніж випадкові відмінності всередині кожної групи. H 1: Відмінності між градаціями фактора (різними умовами) є більш вираженими, ніж випадкові відмінності всередині кожної групи.

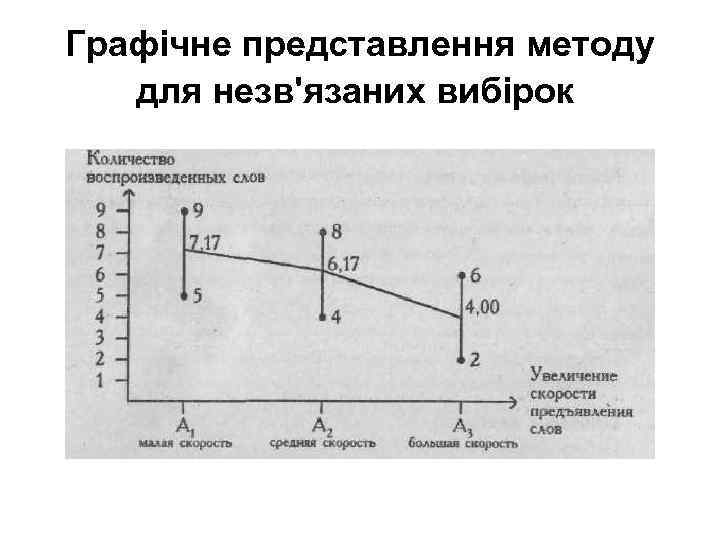Графічне представлення методу для незв'язаних вибірок

Обмеження методу однофакторного дисперсійного аналізу для незв'язаних вибірок • Однофакторний дисперсійний аналіз вимагає не менше трьох градацій фактора і не менше двох випробовуваних в кожної градації.

• Повинне дотримуватися правило рівності дисперсій в кожній комірці дисперсійного комплексу. Умова рівності дисперсій виконується при використанні запропонованої схеми розрахунку за рахунок вирівнювання кількості спостережень в кожному з умов (градацій). • Правомірність цього методичного прийому була обгрунтована Г. Шеффе (1980).

• Результативний ознака повинен бути нормально розподілений в досліджуваній вибірці.

Приклад Три різні групи з шести випробуваних отримали списки з десяти слів. Першій групі слова пред'являлися з низькою швидкістю 1 слово в 5 секунд, другій групі із середньою швидкістю 1 слово в 2 секунди, і третій групі з великою швидкістю 1 слово в секунду. Було передбачено, що показники відтворення будуть залежати від швидкості пред'явлення слів. Результати представлені в Табл. 7. 2.

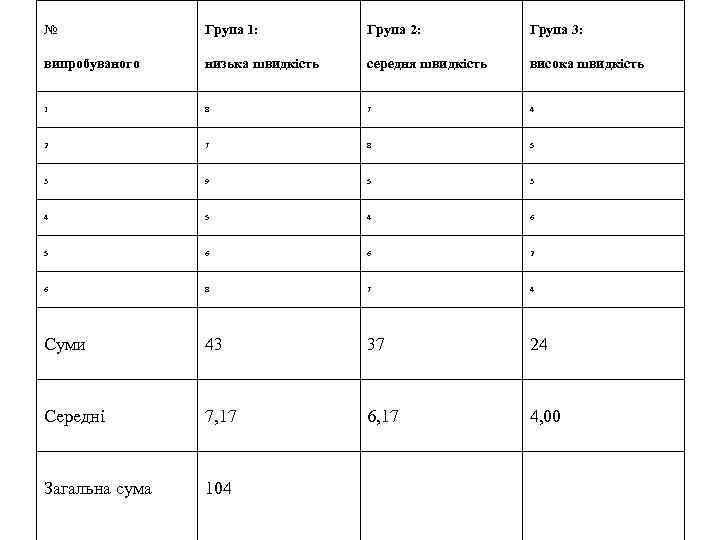№ Група 1: Група 2: Група 3: випробуваного низька швидкість середня швидкість висока швидкість 1 8 7 4 2 7 8 5 3 9 5 3 4 5 4 6 5 6 6 2 6 8 7 4 Суми 43 37 24 Середні 7, 17 6, 17 4, 00 Загальна сума 104

• Оскільки зіставляються різні групи, будь які відмінності в показниках між різними умовами пред'явлення слів це в той же час відмінності між групами випробуваних. Однак всякі відмінності між випробуваними всередині кожної групи пояснюються якимись іншими, не відносяться до справи змінними, будь то індивідуальні відмінності між окремими випробуваними або неконтрольовані фактори, що змушують їх реагувати різним чином. Критерій F дозволяєперевірити гіпотези: Але: Відмінності в обсязі відтворення слів між групами є не більш вираженими, ніж випадкові відмінності всередині кожної групи. Н 1: Відмінності в обсязі відтворення слів між групами є більш вираженими, ніж випадкові відмінності всередині кожної групи. Використовуючи експериментальні значення, представлені в Табл. 7. 2, встановимо деякі величини, які будуть необхідні для розрахунку критерію F.

Поз нач енн я T c Розшифровка позначення ^ Експер имента льні значенн я Суми 43; 37; індивідуальних 24 значень по кожному з умови Σ (T Сума квадратів 2 сумарних значень c) по кожному з умов Σ (T 2 c) = 43 2 +37 2+24 2 C c = 3 Кількість умов

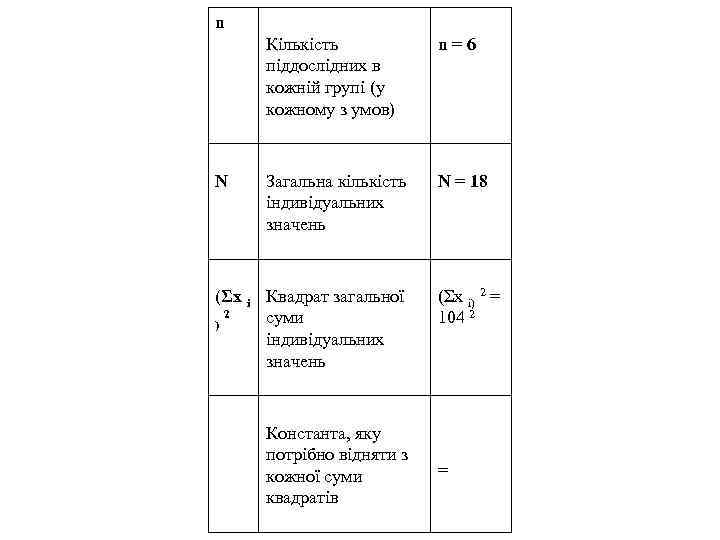n Кількість піддослідних в кожній групі (у кожному з умов) N n = 6 Загальна кількість індивідуальних значень N = 18 (Σx i Квадрат загальної 2 суми ) індивідуальних значень (Σx i) 2 = 104 2 Константа, яку потрібно відняти з кожної суми квадратів =

x i Кожне індивідуальне значення Σ (x Сума квадратів 2) індивідуальних i значень

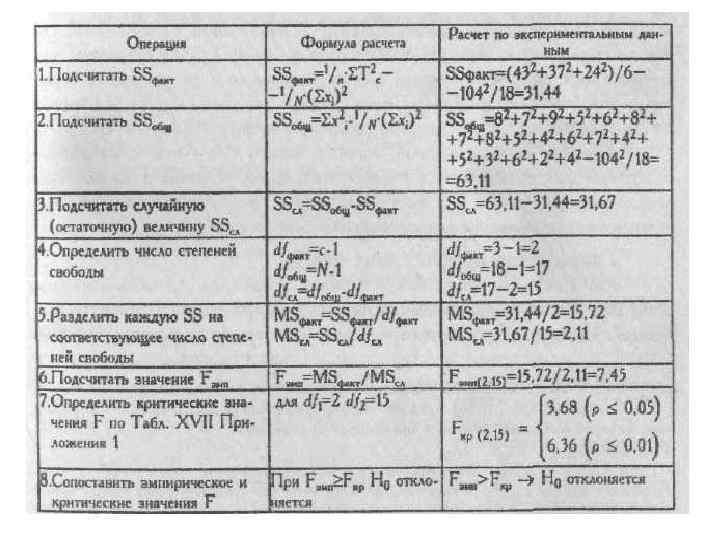
• Висновок: Н 0 відхиляється. Приймається H 1. Відмінності в обсязі відтворення слів між групами є більш вираженими, ніж випадкові відмінності всередині кожної групи (р <0, 01). Отже, швидкість пред'явлення слів впливає на обсяг їх відтворення 5.

Дисперсійний аналіз для зв'язаних вибірок • Призначення методу Метод дисперсійного аналізу для зв'язаних вибірок застосовується в тих випадках, коли досліджується вплив різних градацій фактора або різних умов наодну і ту ж вибірку випробовуваних. Градацій фактора повинно бути не менше трьох. Непараметричний варіант цього виду аналізу критерій Фрідмана χ 2 r.

Опис методу • В даному випадку відмінності між випробуваними можливий самостійний джерело відмінностей. У схемі однофакторного аналізу для незв'язаних вибірок відмінності між умовами в той же час відображували відмінності між випробуваними. Тепер відмінності між умовами можуть проявитися лише всупереч розбіжностям між випробуваними. Фактор індивідуальних відмінностей може виявитися більш значущим, ніж фактор зміни експериментальних умов. Тому нам необхідно враховувати ще одну величину суму квадратів сум індивідуальних значень випробуваних.

Призначення методу • Метод дисперсійного аналізу для зв'язаних вибірок застосовується в тих випадках, коли досліджується вплив різних градацій фактора або різних умов наодну і ту ж вибірку випробовуваних. Градацій фактора повинно бути не менше трьох. Непараметричний варіант цього виду аналізу критерій Фрідмана χ 2 r.

Опис методу • В даному випадку відмінності між випробуваними можливий самостійний джерело відмінностей. У схемі однофакторного аналізу для незв'язаних вибірок відмінності між умовами в той же час відображували відмінності між випробуваними. Тепер відмінності між умовами можуть проявитися лише всупереч розбіжностям між випробуваними. Фактор індивідуальних відмінностей може виявитися більш значущим, ніж фактор зміни експериментальних умов. Тому нам необхідно враховувати ще одну величину суму квадратів сум індивідуальних значень випробуваних.

Графічне представлення методу На Рис. 7. 3 представлена крива зміни часу рішення анаграм різної довжини: чотирибуквений, пятібуквенних і шестібуквенной. Однофакторний дисперсійний аналіз для зв'язаних вибірок дозволить визначити, що переважує тенденція, виражена цією кривою, або індивідуальні відмінності, діапазон яких представлений на графіку у вигляді вертикальних ліній від мінімального до максимального значення.

Обмеження методу дисперсійного аналізу для зв'язаних вибірок • • • Дисперсійний аналіз для зв'язаних вибірок вимагає не менше трьох градацій фактора і не менше двох випробовуваних, які зазнали впливу кожної з градацій фактора. Повинне дотримуватися правило рівності дисперсій в кожній комірці комплексу. Ця умова побічно виконується за рахунок однакової кількості спостережень у кожному осередку комплексу. Пропонована схема розрахунку орієнтована тільки на такі рівномірні комплекси. Результативний ознака повинен бути нормально розподілений в досліджуваній вибірці.

Подсчет в программе • Для того, чтобы рассчитать однофакторный дисперсинный анализ используя статистически пакет SPSS необходимо сделать следующий шаги: • 1. Внести значения переменных в таблицу Data Editor. (Например 2 переменных var 1 и var 2) • 2. Выбираем Analyze > Compare means > One Way ANOVA… • 3. В появившемся окне под переносим переменную на которую происходит влияние (зависимую переменную) в правое верхнее окно Dependent List • 3. 1. Переменную которая «влияет» или является причиной переносим в нижнее окно Factor • 4. Нажимаем кнопку Options… • 4. 1. В появившемся окне выбираем Descriptive, Homogeneity of variance test, Mean plot. • 4. 2. Нажимаем Continue

• 4. 1. В появившемся окне выбираем Descriptive, Homogeneity of variance test, Mean plot. • 4. 2. Нажимаем Continue • 5. Нажимаем кнопку Ok • 6. Смотрим результаты [cta id=" "]

Решение прикладных задач средствами EXCEL. • В MS Excel для проведения однофакторного дисперсионного анализа использует ся процедура. Однофакторный дисперсионный анализ. • Для проведения дисперсионного анализа необходимо: • • ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соот ветствующие одному значению исследуемого фактора, а столбцы располагались в порядке возрастания (убывания) величины исследуемого фактора, • • выполнить команду Сервис > Анализ данных;

• появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК; • • в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши; • • в разделе Группировка переключатель установить в положение по столбцам;

• • • указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кноп кой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верх нюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведе но сообщение в случае возможного наложения выходного диапазона на исход ные данные. • нажать кнопку ОК. Результаты анализа. Выходной диапазон будет включать в себя результаты дис персионного анализа: средние, дисперсии, критерий Фишера и другие показатели. Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперси онный анализ на пересечении строки ежду группами и столбца РМ Значение. В случаях, когда Р Значение < 0, 05, критерий Фишера значим, и влияние исследуемого фак тора можно считать доказанным.

• Задача № 1. • Изучалось различие в продуктивности воспроизведения одного и того же материала трех групп испытуемых (по 5 человек), различающихся условиями предъявления этого материала для запоминания. Результаты обследования приведены в таблице. • •

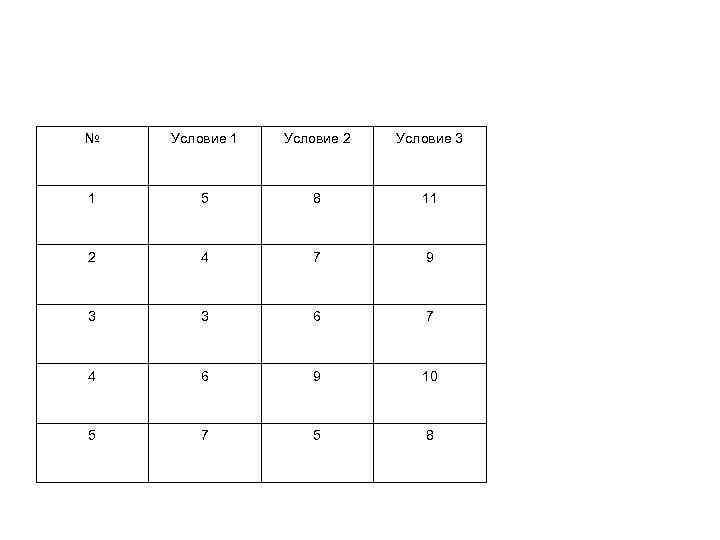№ Условие 1 Условие 2 Условие 3 1 5 8 11 2 4 7 9 3 3 6 7 4 6 9 10 5 7 5 8

• Проверить гипотезу о том, что продуктивность воспроизведения материала зависит от условий его предъявления. • Решение: • Формулируем гипотезы: • H – продуктивность воспроизведения материала не зависит от условий его предъявления. • H – продуктивность воспроизведения материала зависит от условий его предъявления. • 1. Исследуемые данные введите в рабочую таблицу Excel по столбцам: в столбец А — данные по Условию 1, в столбец В — данные по Условию 2, в столбец С – данные по Условию 3 (диапазон А 1 -С 6). • 2. Выполните команду Сервис ► Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа щелчком мыши выберите процедуру Однофакторный дисперсионный анализ. Нажмите кнопку ОК.

• 3. В появившемся диалоговом окне Однофакторный дисперсионный анализ в поле Входной интервал задайте. А 2 С 6. Для этого наведите указатель мыши на ячейку А 2 и протяните его к ячейке С 6 при нажатой левой кнопке мыши.

• В разделе Группировка переключатель установите в положение по столбцам. • 5. Далее необходимо указать выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал (наведите указатель мыши и щелкните левой кнопкой), затем щелкните указателем мыши в правом поле ввода Выходной интервал, и щелчком мыши на ячейке А 8 укажите расположение выходного диапазона. Нажмите кнопку ОК.

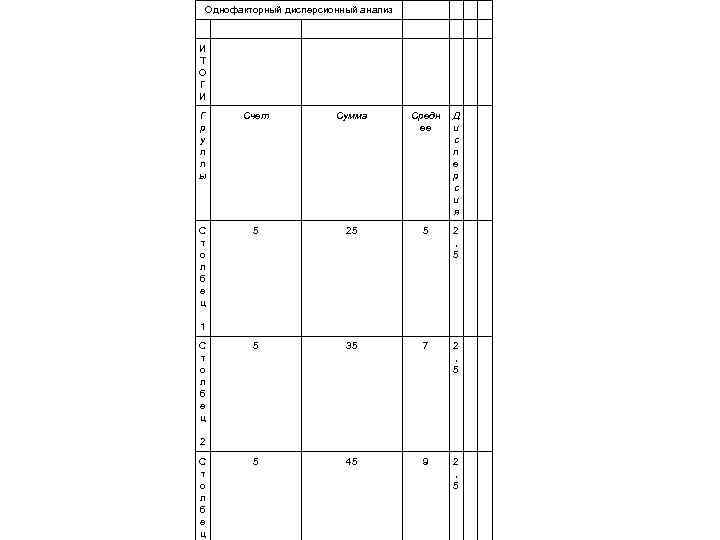Однофакторный дисперсионный анализ И Т О Г И Г р у п п ы Счет Сумма Средн ее Д и с п е р с и я С т о л б е ц 1 5 25 5 2 , 5 С т о л б е ц 2 5 35 7 2 , 5 С т о л б е ц 5 45 9 2 , 5

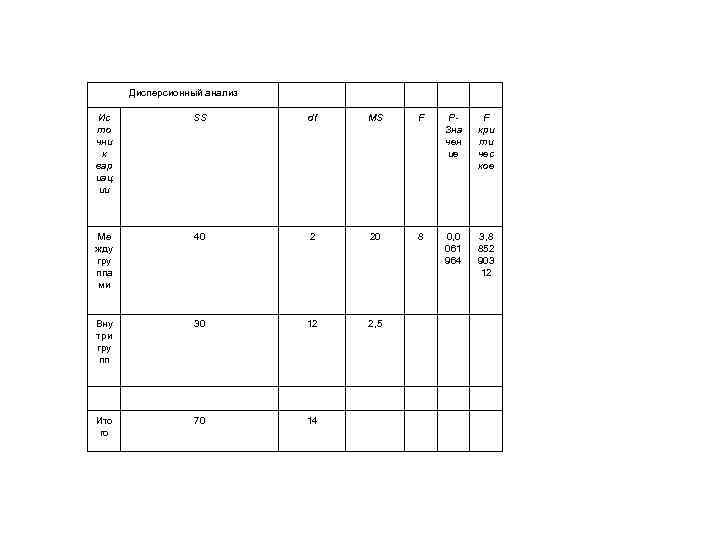Дисперсионный анализ Ис то чни к вар иац ии SS df MS F PЗна чен ие F кри ти чес кое Ме жду гру ппа ми 40 2 20 8 0, 0 061 964 3, 8 852 903 12 Вну три гру пп 30 12 2, 5 Ито го 70 14

Интерпретация результатов. • В таблице Дисперсионный анализ на пересечении строки Между группами и столбца Р-Значение находится величина 0, 000729. Величина Р-Значение < 0, 01, следовательно, критерий Фишера значим, и обнаружено статистически достоверное влияние условий предъявления материала на продуктивность его воспроизведения. •