Тема 2 2 Влияние Земли на распространение радиоволн

Тема 2. 2 Влияние Земли на распространение радиоволн Лекции № 26 Результирующее поле излучателей, поднятых над поверхностью Земли 1. Допустимая высота неровностей земной поверхности для зеркального отражения радиоволн. 2. Результирующее поле излучателей, поднятых на земной поверхностью.

Вопрос 1 Допустимая высота неровностей земной поверхности для зеркального отражения радиоволн

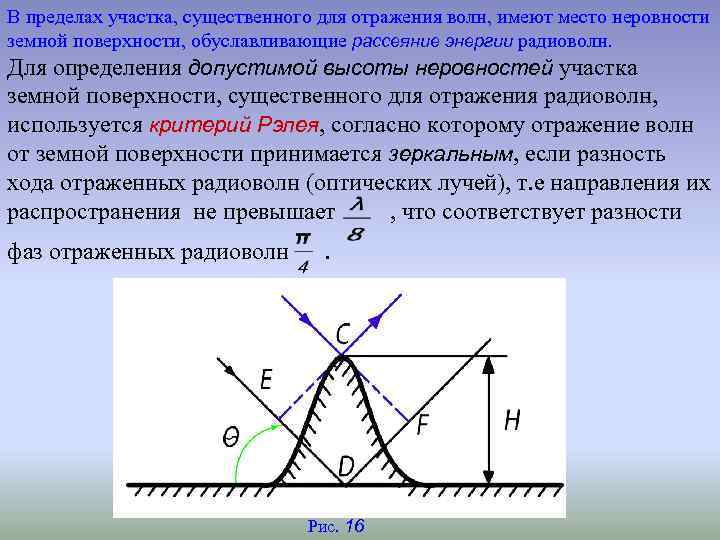В пределах участка, существенного для отражения волн, имеют место неровности земной поверхности, обуславливающие рассеяние энергии радиоволн. Для определения допустимой высоты неровностей участка земной поверхности, существенного для отражения радиоволн, используется критерий Рэлея, согласно которому отражение волн от земной поверхности принимается зеркальным, если разность хода отраженных радиоволн (оптических лучей), т. е направления их распространения не превышает , что соответствует разности фаз отраженных радиоволн . Рис. 16

Разность хода лучей, зеркально отраженных от плоской земной поверхности и вершины неровности (см. рис. 16), равна: (1. 28) Отражение радиоволн можно считать зеркальным, если выполняется условие: (1. 29) Выражение для допустимой высоты неровностей участка земной поверхности, существенного для зеркального отражения радиоволн, имеет вид: (1. 30) При малых углах скольжения θ, когда x 0 >> h и sinθ ≈ x 0 /h (см. рис. 15, б): (1. 31) Вывод: допустимая высота неровностей участка земной поверхности, существенного для зеркального отражения радиоволн зависит не только от длины волны (λ), но от угла скольжения (θ). С уменьшением угла скольжения (удалением точки отражения радиоволны от антенны) высота допустимых неровностей (HД ) увеличивается.

Вопрос 2 Результирующее поле излучателей, поднятых на земной поверхностью

При наличии прямой и отраженной радиоволн результирующее поле в точке наблюдения (В) представляет собой результат интерференции (сложения) этих волн. Определим результирующее поле. 2. 1 Интерференционный множитель Рис. 17

Пусть в точке А (см. рис. 17) расположен излучатель радиоволн, у которого характеристики и параметры определяющие его направленные свойства (нормированная диаграмма направленности F(θ, φ), максимальный коэффициент направленного действия Dmax, излучаемая мощность PΣ ) заранее известны. Направление максимального излучения относительно линии горизонта (главного лепестка ДН излучателя) характеризуется углом θm. Земную поверхность будем считать идеально плоской с электрическими параметрами ε и σ. Требуется найти напряженность результирующего электрического поля в точке наблюдения В, расположенной в дальней зоне относительно излучателя. В данном случае: (1. 32) где: (1. 33) (1. 34)

Если расстояние до точки наблюдения значительно больше высоты излучателя (r 1 >> h), то в амплитудных множителях (1. 33 и 1. 34) разностью хода лучей r 1 и r 2 можно пренебречь полагая r 1 ≈ r 2 ≈ r. В фазовых множителях (1. 33 и 1. 34) подобное приближение допустимо, так как разность хода прямой и отраженной радиоволн составляет величину сравнимую с рабочей длиной радиоволны (λ). В результате выражение для напряженности результирующего электрического поля в точке наблюдения В принимает следующий вид: (1. 35) Первый множитель в (1. 35), стоящий перед квадратными скобками, определяет величину напряженности поля излучателя в свободном пространстве, а второй множитель, учитывающий влияние земной поверхности на результирующее поле в точке наблюдения В называется интерференционным множителем.

Интерференционный множитель как комплексную величину общем случае можно представить следующей формулой: (1. 36) Модуль интерференционного множителя имеет вид: (1. 37) Фаза интерференционного множителя имеет вид (1. 38)

где: Результирующая нормированная диаграмма направленности (ДН) излучателя А (далее – результирующая ДН) при интерференции прямой и отраженной радиоволны в данном случае имеет выражение: (1. 39)

2. 1 Анализ интерференционного множителя Рассмотрим два наиболее характерных случая ориентации максимума главного лепестка ДН излучателя А (антенны) в пространстве. 1. θm ≥ θ 0 где: (см. рис. 18) θ 0 – половина ширины главного лепестка ДН антенны по нулевому уровню излучаемой мощности. h Рис. 18

Земная поверхность в данном случае не облучается главным лепестком ДН излучателя А (антенны) и не влияет на его направленные свойства (результирующее поле в точке наблюдения). При этом отражение радиоволн от земной поверхности отсутствует (см. 1. 37). 2. θm ≥ θ 0 A h Рис. 19 (см. рис. 19)

На практике этот случай характерен для антенн радиолокационных станций (РЛС) обнаружения и сопровождения низколетящих воздушных объектов, а также при организации наземной радиосвязи. Поверхность Земли в данном случае облучается главным лепестком ДН излучателя А (антенны). В данном случае излучатель А (антенна) имеет осесимметричную ДН: Согласно 1. 37 модуль интерференционного множителя имеет вид: (1. 40) Выражение для результирующей ДН антенны в вертикальной плоскости может быть записано в виде: Проведем анализ выражения (1. 40).

При h >> λ приближенно можно считать, что максимумы и минимумы (экстремумы) модуля интерференционного множителя (1. 40) имеют место при выполнении соответственно условий: Направления экстремумов модуля интерференционного множителя определяются соотношениями: (1. 41) (1. 42) где: n - номер максимума (минимума) модуля интерференционного множителя (n = 1, 2, 3, …).

Из выражений (1. 41) и (1. 42) получаем: (1. 43) (1. 44) (максимальные и минимальные) интерференционного множителя в данном случае равны: Экстремальные значения модуля (1. 45) (1. 46)

Следовательно, модуль интерференционного множителя имеет многолепестковую структуру. Количество лепестков N интерференционного множителя определяется наибольшим значением n без единицы, при котором выполняется условие: Тогда количество лепестков N модуля интерференционного множителя определяется приближенной формулой: (1. 47) где: – волновая высота излучателя (антенны). Из выражения (1. 47) видно, что количество лепестков модуля интерференционного множителя равно числу полуволн, укладывающихся по высоте антенны.

Проведем анализ модуля интерференционного множителя для различной удельной проводимости земной поверхности (σ) и в зависимости от типа линейной поляризации радиоволн (В, Г). 2. 1. Горизонтальная поляризация радиоволн (Г) а) Земная поверхность – идеальный проводник (σ = ∞) В данном случае Тогда модуль интерференционного множителя имеет вид: (1. 48) Направления максимумов и минимумов интерференционного множителя согласно выражениям (1. 43) и (1. 44) определяются соотношениями: (1. 49) (1. 50)

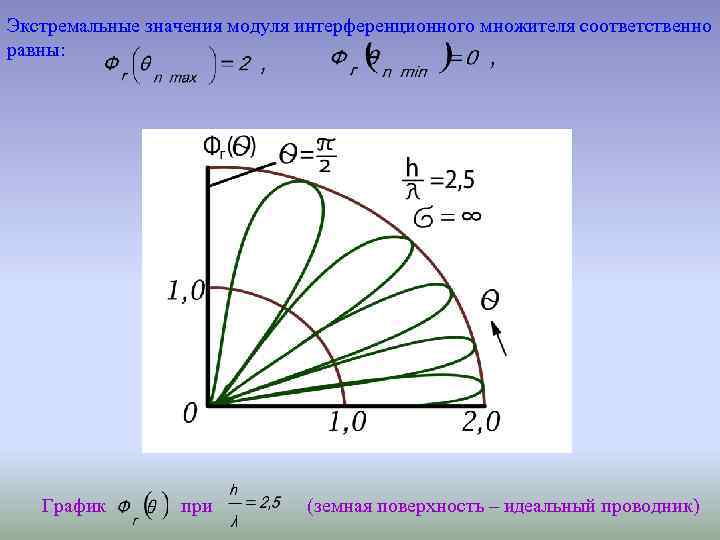Экстремальные значения модуля интерференционного множителя соответственно равны: График при (земная поверхность – идеальный проводник)

Выводы по 2. 1. а): • При увеличении волновой высоты излучателя А (передающей антенны) лепестки модуля интерференционного множителя «прижимаются» к земной поверхности, что приводит к увеличению напряженности поля в точке наблюдения Ер(В) и к дальности действия РЛС на малых высотах. • В направлении максимумов модуля интерференционного множителя напряженность поля излучения излучателя А (передающей антенны) в точке наблюдения Ер(В) в два раза больше, чем напряженность поля при распространении радиоволн без их отражения от земной поверхности – Еп(В). В направлении минимумов модуля интерференционного множителя излучение излучателя А отсутствует.

2. 1. Горизонтальная поляризация радиоволн (Г) б) Земная поверхность – реальный диэлектрик (60σ·λ << ε ) В данном случае . Направления максимумов и минимумов модуля интерференционного множителя определяются выражениями (1. 49) и (1. 50): (1. 51) (1. 52)

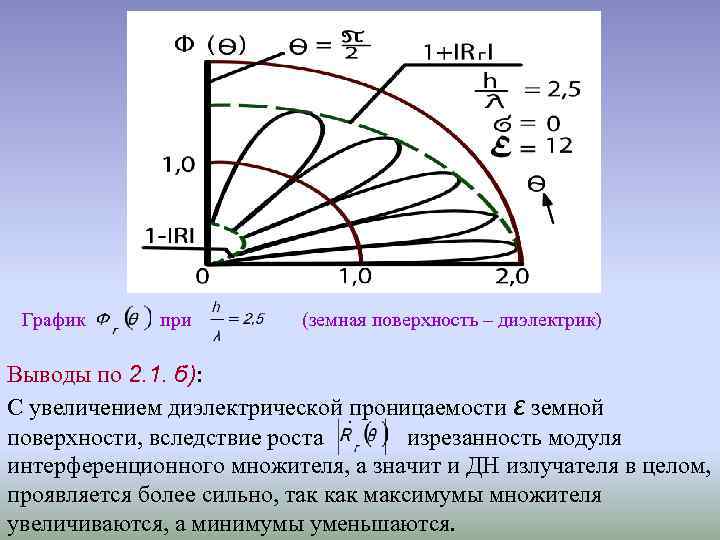График при (земная поверхность – диэлектрик) Выводы по 2. 1. б): С увеличением диэлектрической проницаемости ε земной поверхности, вследствие роста изрезанность модуля интерференционного множителя, а значит и ДН излучателя в целом, проявляется более сильно, так как максимумы множителя увеличиваются, а минимумы уменьшаются.

2. 1. Горизонтальная поляризация радиоволн (Г) в) Земная поверхность – полупроводник (60σ·λ ≈ ε ) В данном случае . Значения максимумов и минимумов модуля интерференционного множителя мало отличается от значений интерференционного множителя в случае диэлектрической земной поверхности и определяются выражениями (1. 51) и (1. 52). Выводы по 2. 1. в): С увеличением проводимости почвы σ изрезанность модуля интерференционного множителя, а также ДН излучателя (передающей антенны) проявляется более сильно, так как при σ1 > σ2

2. 2. Вертикальная поляризация радиоволн (В) а) Земная поверхность – идеальный проводник (σ = ∞) В данном случае имеем: Модуль интерференционного множителя, с учетом выражения (1. 40), имеет вид: (1. 53) Направления максимумов и минимумов интерференционного множителя согласно выражениям (1. 43) и (1. 44) определяются соотношениями: (1. 54) (1. 55) где: n - номер максимума (минимума) модуля интерференционного множителя (n = 1, 2, 3, …).

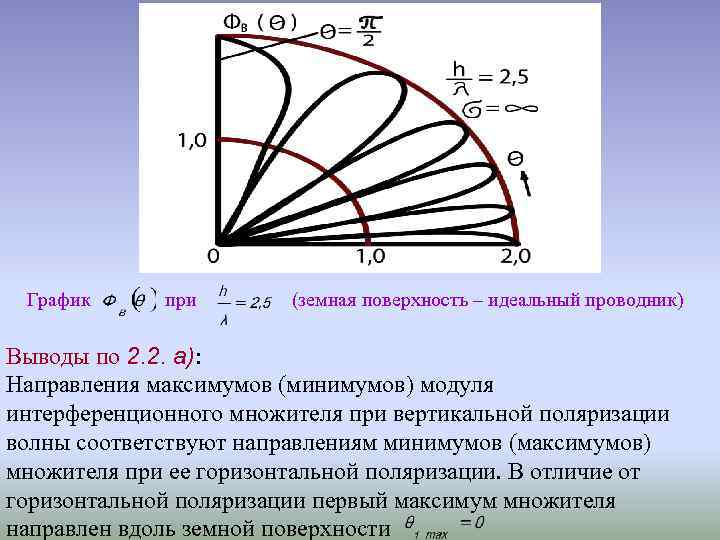График при (земная поверхность – идеальный проводник) Выводы по 2. 2. а): Направления максимумов (минимумов) модуля интерференционного множителя при вертикальной поляризации волны соответствуют направлениям минимумов (максимумов) множителя при ее горизонтальной поляризации. В отличие от горизонтальной поляризации первый максимум множителя направлен вдоль земной поверхности

2. 2. Вертикальная поляризация радиоволн (В) б) Земная поверхность – реальный диэлектрик (60σ·λ << ε ) В данном случае где: – угол Брюстера, при котором . Модуль интерференционного множителя, с учетом выражения (1. 40), имеет вид: (1. 56) Знак минус в выражении (1. 56) соответствует интервалу углов а знак плюс – . ,

График при , (земная поверхность – идеальный проводник) Выводы по 2. 2. б): Для интервалов направления максимумов и минимумов модуля интерференционного множителя определяются выражениями (1. 49) и (1. 50), а для углов скольжения – выражениями (1. 54) и (1. 55). Соответственно значение определяются выражениями (1. 51) и (1. 52).

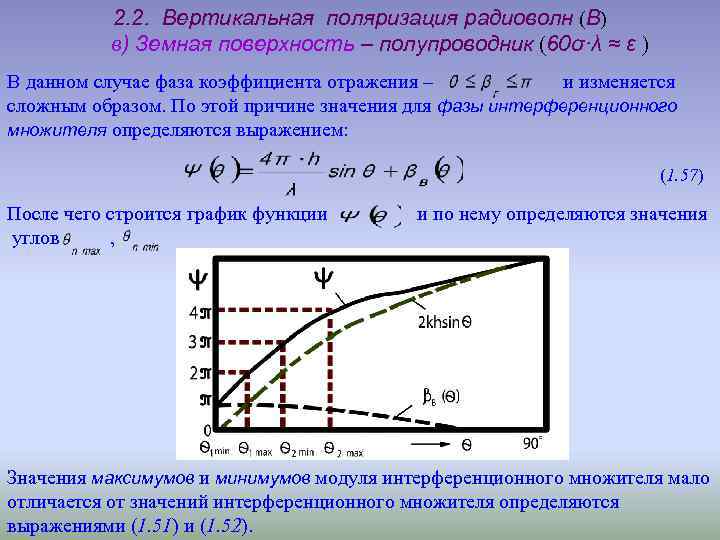2. 2. Вертикальная поляризация радиоволн (В) в) Земная поверхность – полупроводник (60σ·λ ≈ ε ) В данном случае фаза коэффициента отражения – и изменяется сложным образом. По этой причине значения для фазы интерференционного множителя определяются выражением: (1. 57) После чего строится график функции углов , и по нему определяются значения Значения максимумов и минимумов модуля интерференционного множителя мало отличается от значений интерференционного множителя определяются выражениями (1. 51) и (1. 52).