Тема 19 Векторная оптимизация и теория принятия решений

Тема 19 Векторная оптимизация и теория принятия решений Ø Принятие решений на основе решения оптимизационной задачи Ø Теория принятия решений Ø Методы многокритериальной оптимизации 2/17/2018 1

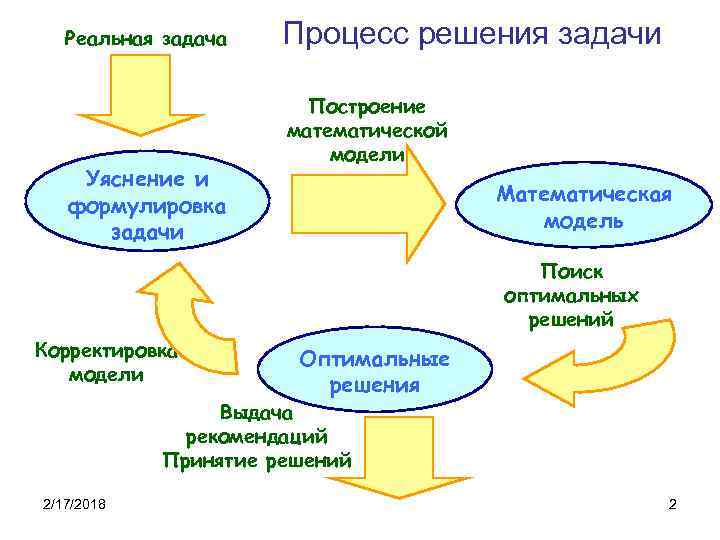Реальная задача Уяснение и формулировка задачи Процесс решения задачи Построение математической модели Математическая модель Поиск оптимальных решений Корректировка модели Оптимальные решения Выдача рекомендаций Принятие решений 2/17/2018 2

Задачи и математические модели Ø В качестве средства достижения своих целей человек создает некую систему – т. е. набор связанных элементов, образующих целостный объект. Ø Реальные задачи как раз и возникают при создании или совершенствовании имеющейся системы. Ø Математическая модель описывает исследуемую систему и позволяет выразить ее эффективность в виде целевой функции Ø Y = f(X), Ø где X = (x 1, …, xn) — входные параметры системы, Ø Y = (y 1, …, yk) — выходные характеристики Ø На переменные x 1, …, xn накладывается ряд ограничений, которые задают область допустимых параметров Ø D={x, g 1 (X) 0, . . gm (X) 0}. 2/17/2018 3

Принятие решений Ø После того, как модель Y = f(X) создана, подставляя некоторый вариант исходных данных X D получают значение выходных параметров Y. Ø Для того, чтобы задуманная исходная цель была достигнута, требуется значения X выбрать такими, чтобы значения выходных параметров y 1, …, yk удовлетворяли определенным критериям. Например, yi

Компьютерные системы поддержки принятия решений Ø Модели современных систем достаточно сложны и для их исследования разрабатываются специализированные компьютерные программы в различных областях: Ø Базы данных, базы знаний, системы бух учета, системы складов и перевозок (логистические), пакеты решения всевозможных уравнений и, наконец, пакеты оптимизации. Ø Все такие пакеты программ и являются по сути компьютерными системами поддержки принятия решений. Их суть в том, чтобы на основе моделирования и оптимизации выбрать наиболее подходящий вариант достижения намеченной цели. Ø В настоящее время большое развитие получили проблемноориентированные программные системы для поддержки принятия решений в конкретной предметной области. Ø Например для поиска перспективных конструкций СВЧ приборов, антенн, систем планирования, диагностики и т. д. 2/17/2018 5

Теория принятия решений Ø Зародилась в 30 -е годы в США для выработки оптимальной стратегии и тактики военных операций и получила название – исследование операций. Ø В рамках этой науки были сформулированы математические постановки и методы решения целого ряда ставших теперь классическими задач и методов их решения Ø А. А. Грешилов. Как принять наилучшее решение в реальных условиях. М: «Радио и связь» 1991. Ø О. И. Ларичев. Теория и методы принятия решений. М: « Логос» . 2003 2/17/2018 6

Метод линейного программирования Ø Задача о диетическом питании (мы знакомились) Ø Задача о планировании выпуска продукции Ø Задача о рюкзаке (об инвестировании) Ø Задача о перевозках Ø Задача о наилучшем использовании станков Ø Задача об оптимальном раскрое Ø Задача о назначениях ( распределении работ) Ø Задача о закреплении самолетов за воздушными линиями 2/17/2018 7

Сетевые задачи (задачи на графах) Ø Задача комивояжера Ø Задача о покупке автомобиля Ø Задача о размещении производства Ø Задача о максимальном потоке Ø Задача о многополюсной цепи с максимальной пропускной способностью 2/17/2018 8

Динамическое программирование Ø Задача об оптимальной загрузке транспортного средства неделимыми предметами Ø Задача о вкладе средств в производство Ø Задача о распределении средств поражения 2/17/2018 9

Методы многокритериальной оптимизации Ø Если целевая функция только одна, т. е. модель имеет вид то имеет место изученная нами однокритериальная оптимизация. Ø Однако, большинство практически важных систем оценивается не одним, а несколькими критериями, в общем случае m критериями и модель имеет вид 2/17/2018 10

Примеры задач с несколькими критериями Ø Усилитель оценивается по двум основным показателям – коэффициент усиления и КПД: y 1=G(x 1. . xn) и y 2= КПД(x 1. . xn) которые в принципе противоречивы. Ø Выпуск продукции на заводе оценивается стоимостью затрат на производство – y 1 и показателем качества, т. е. ценой на рынке y 2. Ø Такие постановки задач приводят к задаче оптимизации с векторной целевой функцией Ø Получить наилучшее решение = найти компромисс между частными критериями. 2/17/2018 11

Подходы к решению Ø Первый подход - сведение многокритериальной задачи к однокритериальной путем свертывания векторного критерия в один скалярный Ø Второй подход –методы не сводящиеся к однокритериальной задаче Ø Нахождение множества эффективных решений множества Паретто и предъявление их эксперту 2/17/2018 12

Множество Паретто • Введем область критериев Df Ø Предпочтение Парето: Ø Вариант x 1 лучше чем x 2 (x 1>x 2) если fi(x 1) fi(x 2) и хотя бы одно строгое. Ø x 1, x 2 несравнимые (противоречивые) - если нельзя установить предпочтение, т. е. имеются Ø и fi(X 1)< fi(X 2) и fj(X 1)> fj(X 2) Ø Множество Xp для которых не существует более предпочтительных (Xp

f 2 x 2 D Df 4 B A f D x 1 4 f 1 В множестве Парето можно установить более мягкие критерии предпочтения. Например та альтернатива лучше, у которой меньше строгих неравенств выполняется. Вот здесь и вступает в действие интуиция эксперта, основанная на большом опыте. 2/17/2018 14

Метод весовых коэффициентов Ø Вводят вектор весовых коэффициентов Ø Величина значения wi определяет важность (вес) i -го критерия оптимальности и задает его предпочтение перед остальными Ø Весовые коэффициенты задает эксперт 2/17/2018 15

Обобщенные критерии Ø Аддитивный критерий оптимальности Ø Мультипликативный критерий Ø Среднестепенной обобщенный критерий 2/17/2018 16

Одна из процедур оценки весовых коэффициентов 2/17/2018 17

Метод -ограничений Ø Выбирается одна из целей как основная, например Ø Остальные целевые функции записываются в виде ограничений Ø Добавляются свои ограничения 2/17/2018 18

Метод -ограничений (продолжение) Ø Подобный подход позволяет определить некое количество неухудшаемых решений даже для случая вогнутой границы Ø Проблемой остается подходящий выбор значений , хотя ограничения ставятся в жесткой форме и более определенно, чем в методе весовых коэффициентов. Для эксперта это бывает проще. 2/17/2018 19

Метод достижения цели Ø Найти оптимальное решение Ø Задается вектор намерений разработчика (каких значений критериев он хотел бы достичь) Ø Задается вектор весовых коэффициентов Ø Найти 2/17/2018 при 20

Программная реализация в Мат. Лаб • [x, f, ga]=fgoalattain(fun, xo, q, w, A, b, • Ae, be, xmi, xma<, nonlcon, options, p 1, p 2, . . >); • [x, f, ga]=fgoalattain(fun, xo, q, w, [], • [], [], nonlcon); 2/17/2018 21

Метод сведения к задаче минимакса • Этот метод находит решение, на котором достигается минимум наихудшего случая. 2/17/2018 22

Пример 2/17/2018 23

• • • function minmax 1; %начальное приближение x 0=[1; 0]; % неравенства A=[3 2]; b=2. 2; xm=[0; 0]; % обращение [x, p]=fminimax(@fu 3, x 0, A, b, [], xm, [] , @nonling) return 2/17/2018 24

• • • function f=fu 3(x) f(1)=(x(1)-1)^2+(x(2)-2)^2 -2. 1; f(2)=x(1)^1. 3+2*x(2)^0. 9 -1; f(3)=1. 7*x(1)+x(2)-0. 25; Return • • • function [c, ceq]=nonling(x) c=[]; %ограничений-неравенств нет %ограничение-равенство: ceq(1)=-exp(x(1))+exp(x(2))-0. 5; return 2/17/2018 25

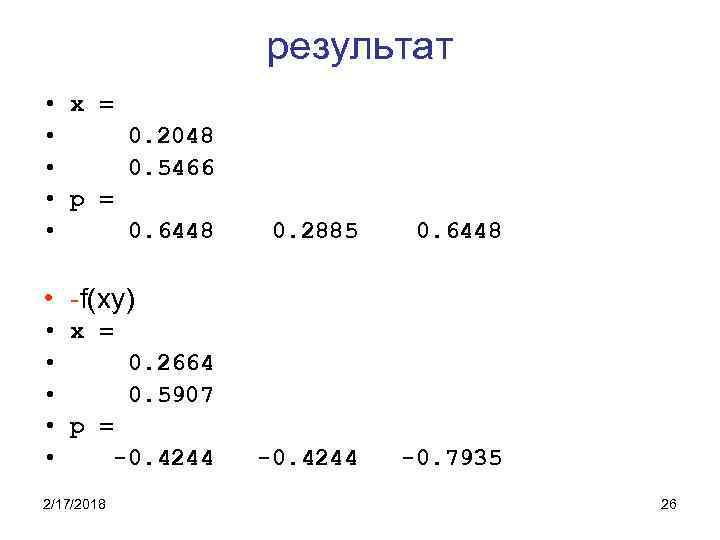результат • x = • 0. 2048 • 0. 5466 • p = • 0. 6448 0. 2885 0. 6448 -0. 4244 -0. 7935 • -f(xy) • x = • 0. 2664 • 0. 5907 • p = • -0. 4244 2/17/2018 26

Конец 2/17/2018 27