Тема 14 Квантовая статистика В квантовой физике статистический

Тема 14. Квантовая статистика. В квантовой физике статистический подход лежит в самой природе микрочастиц, в их волновых свойствах. 1

1. Фермионы подчиняются принципу Паули: в любом квантовом состоянии может находиться не более одной частицы. 2. Бозоны не подчиняются принципу Паули: в любом квантовом состоянии может находиться неограниченное число частиц. 2

§ 14. 1. Фермионы. Электроны в металле. Распределение Ферми-Дирака 3

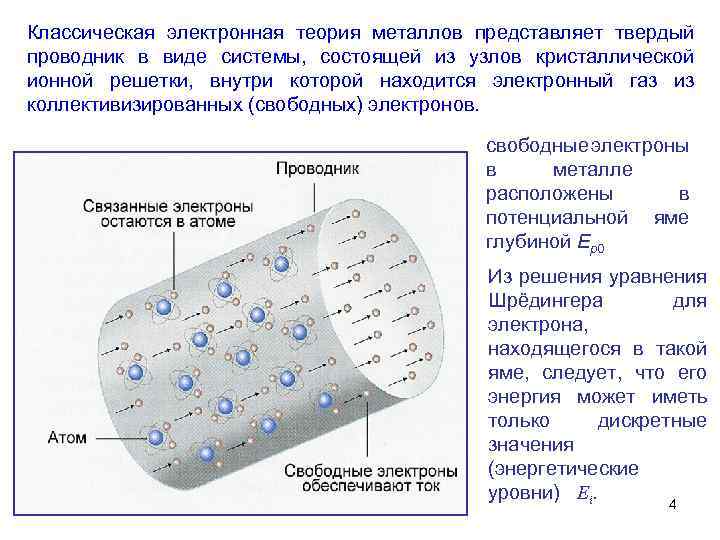Классическая электронная теория металлов представляет твердый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных (свободных) электронов. свободные электроны в металле расположены в потенциальной яме глубиной Ер0 Из решения уравнения Шрёдингера для электрона, находящегося в такой яме, следует, что его энергия может иметь только дискретные значения (энергетические уровни) Ei. 4

- Электроны являются фермионами и подчиняются принципу Паули, согласно которому каждый энергетический уровень заселяется не более чем двумя электронами с противоположными спинами; - энергетический спектр квазинепрерывный; с учетом спина: Распределение Ферми-Дирака определяет среднее число фермионов в состоянии с энергией Ei Паули Вольфганг Эрнст (1890– 1958) Австрийскошвейцарский 5 физик-теоретик

Рассмотрим поведение электронного газа при Т=0 К f(Ei) 2 0 εF E • При температурах Т→ 0 заполнены все состояния с энергией Е< εF 6

Энергия Ферми • энергетический уровень, отделяющий заполненные уровни от пустых при Т = 0 К, называется энергией Ферми • n – концентрация свободных электронов • me - масса электрона Оценим значение энергии Ферми: 7

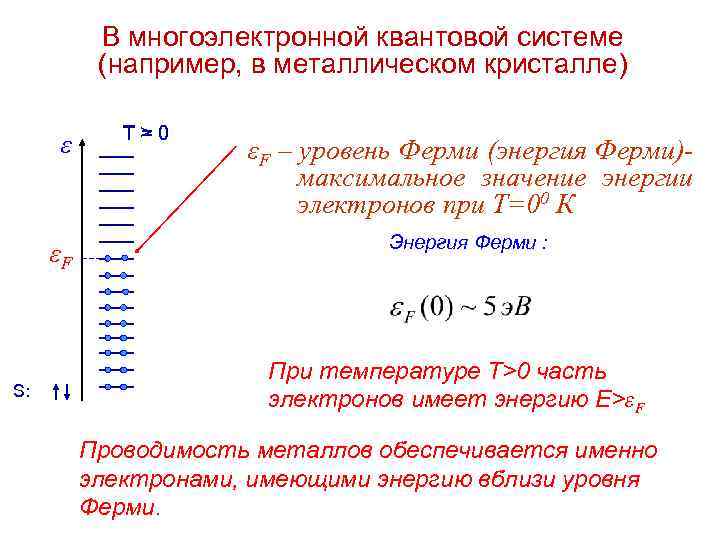В многоэлектронной квантовой системе (например, в металлическом кристалле) ε εF S: T>0 = εF – уровень Ферми (энергия Ферми)максимальное значение энергии электронов при Т=00 К Энергия Ферми : При температуре Т>0 часть электронов имеет энергию Е>εF Проводимость металлов обеспечивается именно электронами, имеющими энергию вблизи уровня Ферми. 8

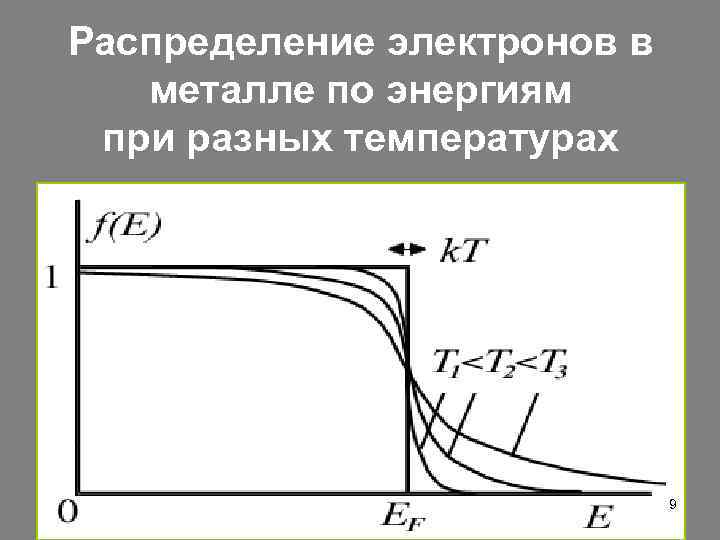Распределение электронов в металле по энергиям при разных температурах 9

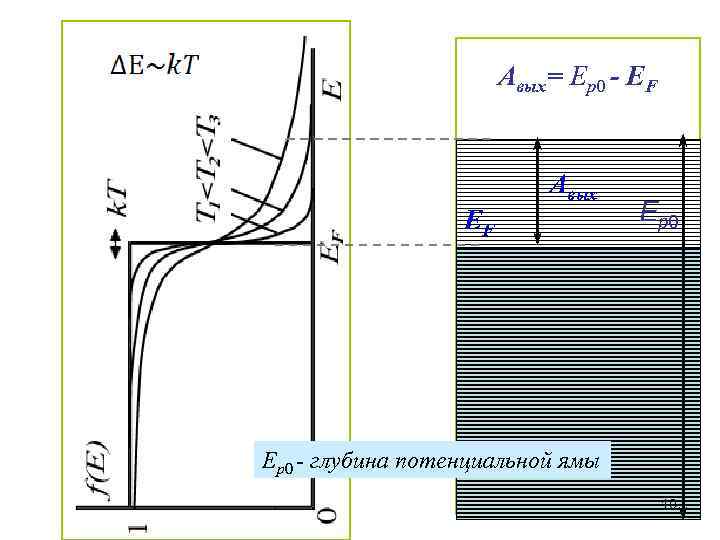Авых= Ер0 - EF EF Aвых Ер0 - глубина потенциальной ямы 10

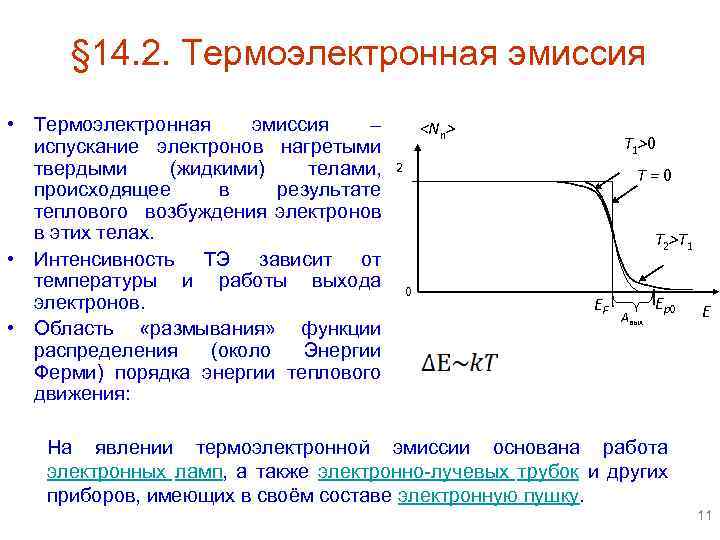§ 14. 2. Термоэлектронная эмиссия • Термоэлектронная эмиссия – испускание электронов нагретыми твердыми (жидкими) телами, происходящее в результате теплового возбуждения электронов в этих телах. • Интенсивность ТЭ зависит от температуры и работы выхода электронов. • Область «размывания» функции распределения (около Энергии Ферми) порядка энергии теплового движения: T 1>0 2 T=0 T 2>Т 1 0 EF Авых Ер0 E На явлении термоэлектронной эмиссии основана работа электронных ламп, а также электронно-лучевых трубок и других приборов, имеющих в своём составе электронную пушку. 11

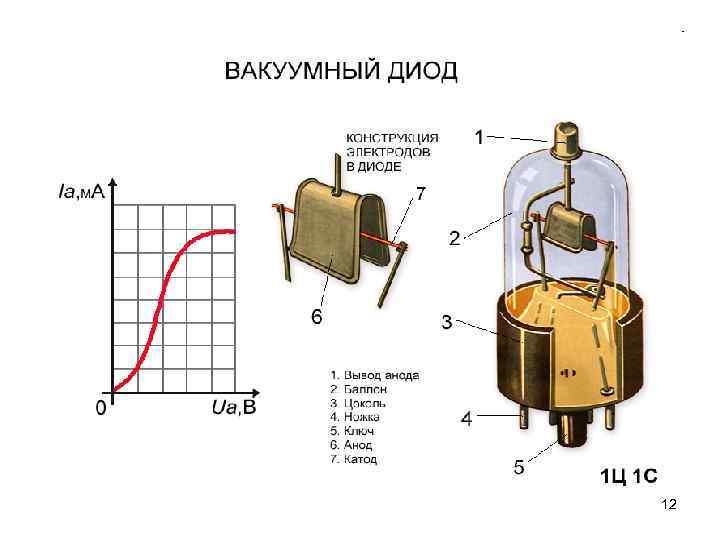12

Плотность тока насыщения определяется формулой Ричардсона — Дешмана: 13

§ 14. 3. Зависимость сопротивления проводников от температуры. Сверхпроводимость Концентрация основных носителей тока - в проводниках практически не температуры: nосн ~ 1022 – 1023 1/м 3 зависит от - Физической причиной электросопротивления металлов является рассеяние электронов на атомах примеси и на узлах кристаллической решетки. ρ = ρколеб +ρприм (ρколеб - сопротивление, обусловленное тепловыми колебаниями решетки, которое растет с ростом температуры) ρ ~ ρ0 (1+αТ) 14

§ 14. 4. Энергетические уровни в атоме и энергетические зоны в кристалле 15

Образование энергетических зон в кристалле 2 Nур ε а ат ом 2 1 ат ом Nур I II в кристалле (N атомов) В кристаллах энергетические спектр электронов распадается на N (число атомов в кристалле) близких уровней «Расстояние» между уровнями внутри зон ~10 – 23 э. В 16

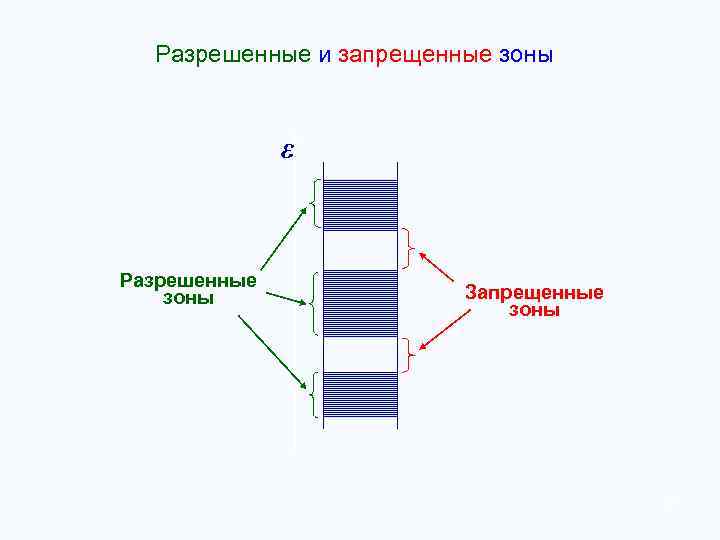Разрешенные и запрещенные зоны ε Разрешенные зоны Запрещенные зоны 17

§ 14. 5. Распределение электронов по квантовым состояниям в кристалле. Проводники и диэлектрики 18

• В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны кристаллы подразделяют на проводники (металлы), полупроводники и диэлектрики. 19

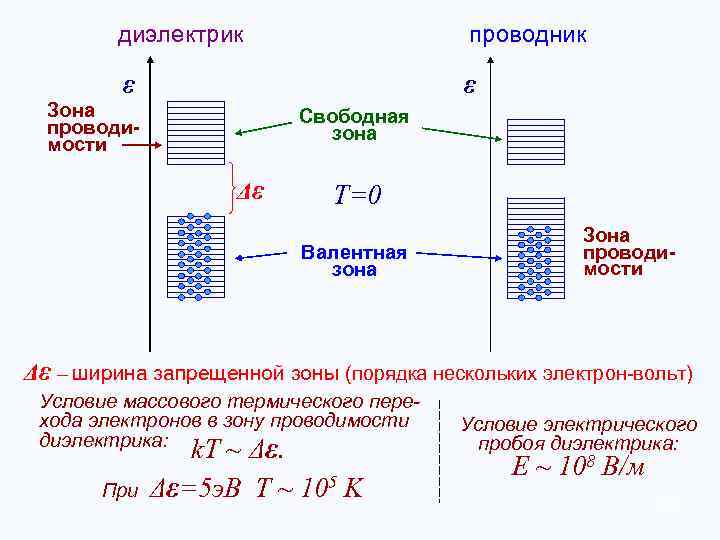диэлектрик проводник ε ε Зона проводимости Свободная зона Δε Т=0 Валентная зона Зона проводимости Δε – ширина запрещенной зоны (порядка нескольких электрон-вольт) Условие массового термического перехода электронов в зону проводимости диэлектрика: При k. T ~ Δε. Δε=5 э. В Т ~ 105 K Условие электрического пробоя диэлектрика: E ~ 108 В/м 20

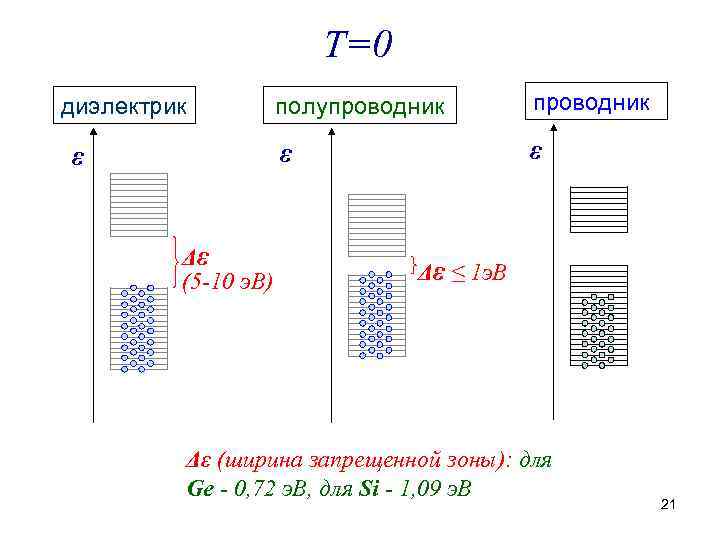Т=0 ε Δε (5 -10 э. В) полупроводник ε диэлектрик ε Δε ≤ 1 э. В Δε (ширина запрещенной зоны): для Ge - 0, 72 э. В, для Si - 1, 09 э. В 21

§ 14. 6. Полупроводники. Электроны и дырки в полупроводниках 22

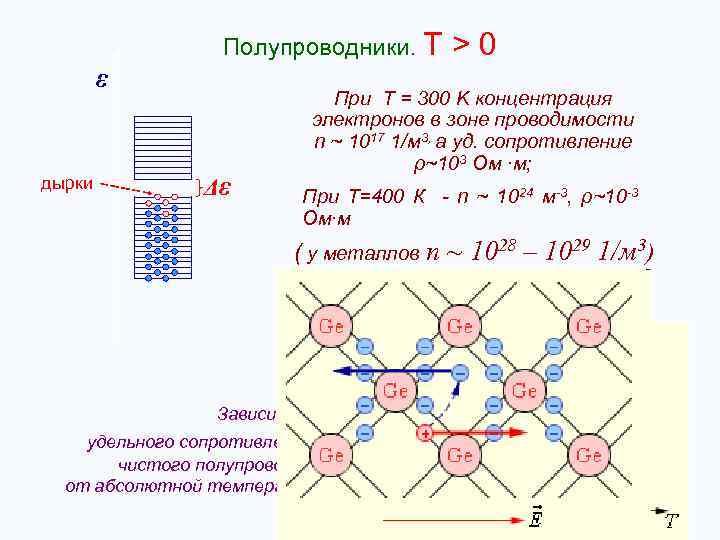Полупроводники. T ε дырки Δε >0 При Т = 300 K концентрация электронов в зоне проводимости n ~ 1017 1/м 3, а уд. сопротивление ρ~103 Ом ∙м; При Т=400 К - n ~ 1024 м-3, ρ~10 -3 Ом∙м ( у металлов n ~ 1028 – 1029 1/м 3) Зависимость удельного сопротивления ρ чистого полупроводника от абсолютной температуры 23

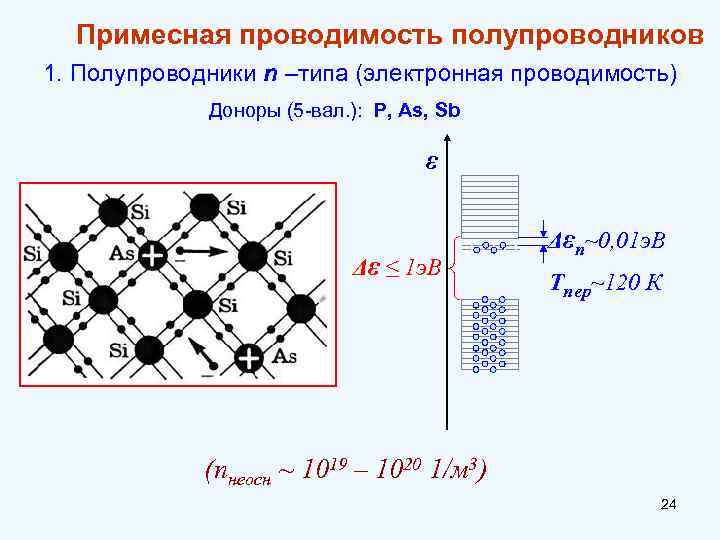Примесная проводимость полупроводников 1. Полупроводники n –типа (электронная проводимость) Доноры (5 -вал. ): P, As, Sb ε Δε ≤ 1 э. В Δεп~0, 01 э. В Тпер~120 К (nнеосн ~ 1019 – 1020 1/м 3) 24

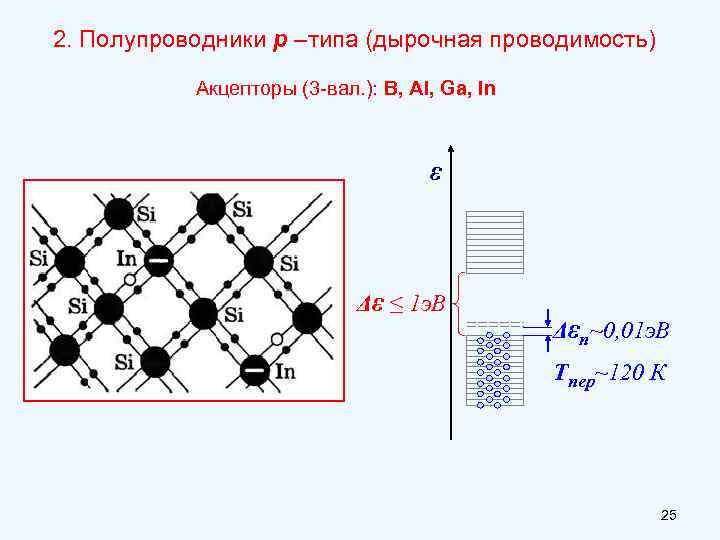2. Полупроводники р –типа (дырочная проводимость) Акцепторы (3 -вал. ): B, Al, Ga, In ε Δε ≤ 1 э. В Δεп~0, 01 э. В Тпер~120 К 25