Тема 10: Олигополия Микроэкономика Тема 10. Олигополия

Тема 10: Олигополия Микроэкономика

Тема 10. Олигополия Равновесие Нэша n Модель Курно n Модель Штэкельберга n Модель Бертрана n Модель ломанной кривой спроса n

1. Равновесие Нэша n Каждая фирма ведет себя наилучшим образом при данном поведении своих конкурентов

2. Модель Курно Предпосылки: 1. Фирмы производят однородный товар 2. Знают кривую рыночного спроса 3. Каждая фирма принимает объем производства конкурента постоянным, а потом принимает собственное решение об объеме производства

2. 1 Типовая задача Допустим, что у нас имеется две фирмы с линейными кривыми спроса P=25 -1/2 Q , а предельные издержки постоянны и равны 10. А) Найдите равновесие по Курно. Б) Найдите равновесие по Штэкельбергу.

Решение: ТR 1 = Pq 1 = (25 -1/2 Q)q 1= [25 -1/2(q 1+q 2)]q 1 = 25 q 1 -1/2 q 12 -1/2 q 1 q 2 n MR 1 = 25 –q 1 -1/2 q 2 n 25 –q 1 -1/2 q 2 =10 n q 1=15 -1/2 q 2 ; q 2=15 -1/2 q 1 n q 1* =10; q 2* =10; Q= q 1*+ q 2* =20 n P= 25 -1/2 Q = 25 - ½(q 1* + q 2* ) =15 n П 1 = 150; П 2 = 150 n

3. Модель Штекельберга Предпосылки модели: n n n На рынке действуют две фирмы, производящие однородный продукт. Фирма L - лидер по объему выпуска; Фирма F - ведомая по объему выпуска. Равновесная цена (Р) на рынке зависит от общего произведенного объема (Q). Выбор выпуска, максимизирующий прибыль ведомого, будет зависеть от выбора, сделанного лидером, q F = f (q L) функция реакции ведомого

Обозначения: Р = P (Q ) – обратная функция рыночного спроса Q = (q L+ q F) – отраслевой выпуск; q. L– объем выпуска лидирующей фирмы; q. F – объем выпуска ведомой фирмы; ПL- прибыль лидера; ПF- прибыль ведомого;

3. 1 Задача b (q. L+ q. F ) P (q. L+ q. F) = a –ведомого ТСL= TCF = 0 ПF = F (q. L, q. F ) = [ a – b (q. L + q. F) ] q. F = a q F - b q. F q. L – b q. F 2 MRF = a - bq. L – 2 bq. F = 0 q. F = (a - bq. L) / 2 b

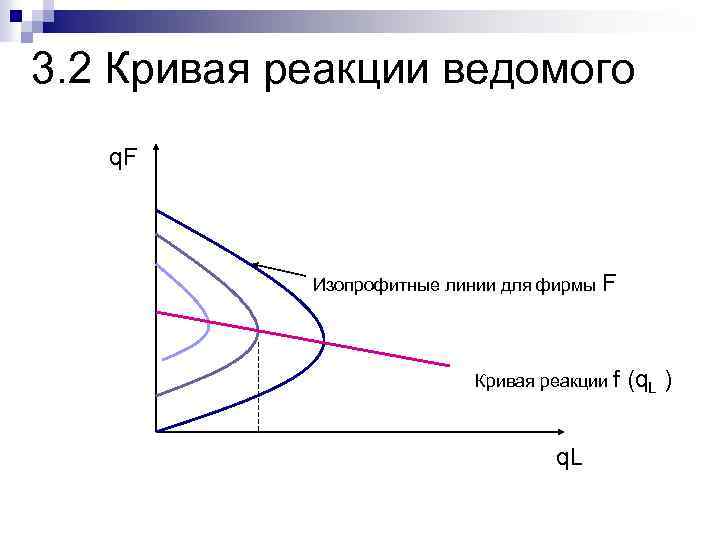3. 2 Кривая реакции ведомого q. F Изопрофитные линии для фирмы F Кривая реакции f q. L (q. L )

3. 3 Задача лидера P (q. L + q. F) q. L- TC →max при q. F = f (q. L) P (q. L + f (q. L ) q. L- TC →max f (q. L ) = q. F = (a - b q. L) / 2 b ПL = F (q. L, q. F ) = [ a – b (q. L + q. F) ] q. L = a q. L – b q. L 2 - b q. F q. L = a q. L – b q. L 2 – (a q. L ) /2 - (b q. L)/2 = (a q. L) /2 - (b q. L)/2 MRL = a/2 - bq L = 0 q. L* = a / 2 b q. F * = a / 4 b q. L*+q. F * = 3 a / 4 b

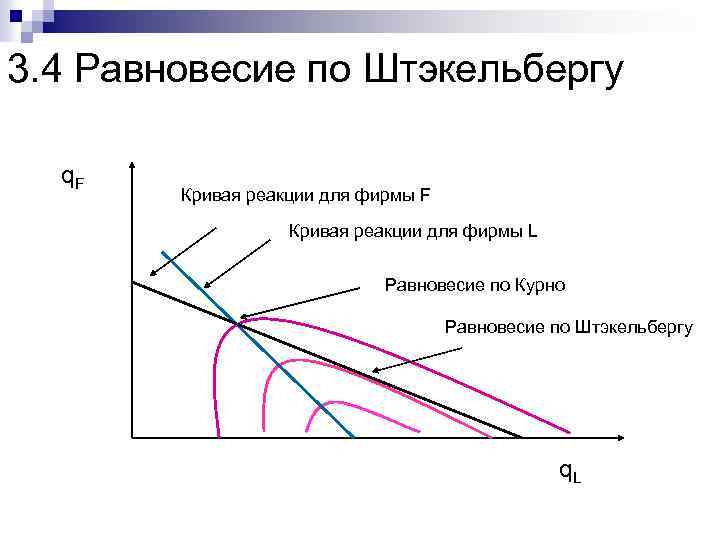3. 4 Равновесие по Штэкельбергу q. F Кривая реакции для фирмы L Равновесие по Курно Равновесие по Штэкельбергу q. L

3. 5 Типовая задача Допустим, что у нас имеется две фирмы с линейными кривыми спроса P=25 -1/2 Q , а предельные издержки постоянны и равны 10. А) Найдите равновесие по Курно. Б) Найдите равновесие по Штэкельбергу.

Решение по Штэкельбергу ТR 1 = Pq 1 = (25 -1/2 Q)q 1= [25 -1/2(q 1+q 2)]q 1 = {25 -1/2[q 1+ (15 -1/2 q 1 )]}q 1 = 25 q 1 -1/2 q 12 – (15/2)q 1 + 1/4 q 12 ; n MR 1 = 25 - q 1 – 15/2 + 1/2 q 1 n 25 - q 1 – 15/2 + 1/2 q 1 =10 n q 1* =15; q 2* =7, 5; Q= q 1*+ q 2* =22, 5 n P= 25 -1/2 Q = 25 - ½(q 1* + q 2* ) =27, 5 n П 1 = 412, 5; П 2 = 206, 25 n

4. Конкуренция не по объему выпуска, а по ценам Ценовая конкуренция в случае однородных товаров ( модель французского экономиста Джозефа Бертрана, 1883 г. ) n Ценовая конкуренция в случае дифференцированных товаров n

4. 1 Ценовая конкуренция в случае однородных товаров Стратегия поведения дуополистов основывается на установлении цен n При снижении цен равновесием Нэша – результат будет конкурентным, т. е цены будут равны предельным издержкам n Обе фирмы получат нулевую прибыль n Поменяв стратегию с выпуска на цену, решение дуополистов существенно меняется n

4. 2 Критика модели Бертрана Когда фирмы производят однородные товары естественно конкурировать с помощью установления количеств. А не цен n Если даже при ценовой конкуренции цены установлены равными, то остается открытым вопрос, какая доля продаж придется на каждую фирму. n

4. 3 Ценовая конкуренция в случае дифференцированных товаров Предположим, что фирмы имеют одинаковые фиксированные издержки, и нулевые предельные n Они сталкиваются с одинаковыми кривыми спроса, например: Q 1 = 0 - 1 P 1 + 2 P 2 Q 2 = 0 - 1 P 2+ 2 P 1 При определении цен можно воспользоваться подходом Курно или Штэкельберга n

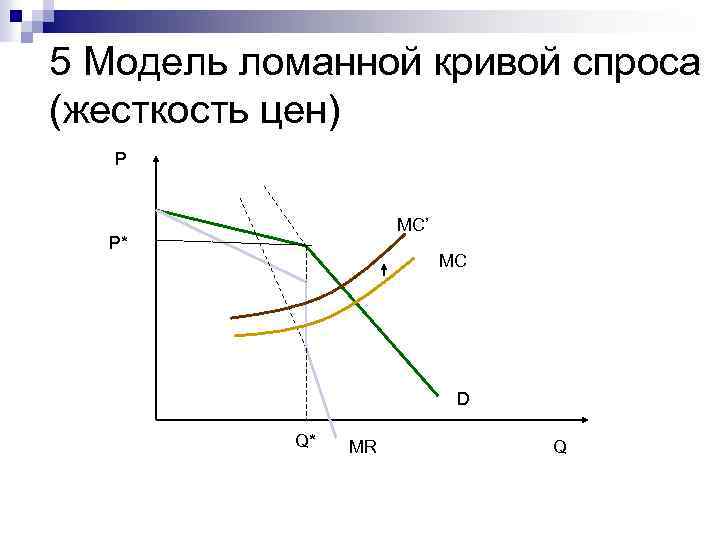5 Модель ломанной кривой спроса (жесткость цен) P MC’ P* MC D Q* MR Q

4. Типовые примеры Допустим, что имеется две фирмы, которые сталкиваются с одинаковыми линейными кривыми спроса Q 1=24 -2 P 1+P 2 и Q 2=24 -2 P 2+P 1 Общие издержки постоянны и равны 100. А) Найти оптимальные ценовые стратегии фирм, используя подходы Курно и Штэкельберга

4. 1 Решение при подходе Курно TR 1 = Q 1 P 1 – ТС =(24 -2 P 1+P 2)P 1 -100 =24 P 1 -2 P 12 +P 2 P 1 -100 n MR 1=24 -4 P 1+P 2=0 n P 1=6+1/4 P 2 n P 2=6+1/4 P 1 n P 1=8; P 2=8 n Q 1 =16 Q 2=16 n П 1=28 П 2 =28 n

4. 2 Решение при подходе Штэкельберга TR 1 = Q 1 P 1=(24 -2 P 1+P 2)P 1=24 P 1 -2 P 12 +P 2 P 1 = 24 P 1 -2 P 12 + 6 P 1+ 1/4 P 1 2 =30 P 17/4 P 12 n MR 1=30 -7/2 P 1=0 n P 1 = 8, 57 P 2=8, 57 n Q 1 = 15, 43 Q 2= Q-Q 1 n