Тема 1 Введение в анализ 1 1

Тема 1. Введение в анализ • 1. 1. Элементы теории множеств • 1. 2. Начала анализа • 1. 3. Функция- определения. Основные свойства. Классификация • 1. 4. Основные элементарные функции • 1. 5. Числовые последовательности. Понятие предела • 1. 6. Понятие предела функции • 1. 7. Методы вычисления пределов. Замечательные пределы • 1. 8. Вычисление пределов. Решение задач Майер И. И. 1

1. 1. Элементы теории множеств Множество - совокупность предметов (объектов), объединенных общим (характеристическим) свойством. Обозначается заглавными буквами А, X, Y Элемент множества – любой его объект. Обозначается строчными буквами a, x, y a A - элемент а входит (принадлежит) в множество А а А - элемент а не принадлежит множеству А. Пустое множество ( )не содержит ни одного элемента В множестве можно выделить подмножества, например в множестве букв (А) можно выделить гласные(Г) и согласные (С). Принадлежность подмножества множеству обозначается Г А Универсальное множество содержит все свои подмножества. Обозначается E или U. Множество может состоять из бесконечного или конечного количества элементов. Счетное множество состоит из элементов, которым можно присвоить порядковые номера Майер И. И. 2

1. 2. Начала анализа. Числовые множества. Числовое множество – множество точек на прямой К числовым множествам относятся: - множество всех натуральных чисел N (счетное); - множество всех целых чисел Z (счетное); - множество всех рациональных чисел Q (счетное); - множество всех действительных чисел R (несчетное); Очевидно, что N Z Q R В множестве можно выделить подмножества: - открытый интервал (числовой промежуток), (а, b). Это множество чисел х, удовлетворяющих неравенствам а<х

Числовые интервалы можно изобразить геометрически на числовой прямой: Окрестность точки х0 - любой открытый интервал, содержащий эту точку. Открытый интервал (а, b) служит окрестностью всякой принадлежащей ему точки: ε-окрестность точки х0 - открытый интервал с центром в точке х0 длиной 2ε, то есть интервал (х0 -ε, х0+ε). Майер И. И. 4

1. 1. Элементы теории множеств Отображение – фундаментальное свойство в теории множеств. Обозначает правило, по которому каждому элементу одного множества (обозначаемого А или Х) ставится в соответствие один элемент другого множества (В , Y). Записывают это правило f: A B (f: Х Y), y = f (x) С этим свойством связано определение: - Числовой функции - Числовой последовательности Майер И. И. 5

1. 3. Функция- определения. Определение функции: Если каждому элементу x множества X ставится в соответствие один элемент y из множества Y, то на множестве X задана функция y = f(x). В функциональном анализе: x - независимая переменная, аргумент; множество значений Х - это область определения функции, ООФ , D ; y - зависимая переменная, значение функции, функция; множество значений Y – область значений, ОЗФ, , или Е. График функции Гf - третье множество, которое определяет функцию. Функция определена, если заданы ООФ , ОЗФ, Гf. Числовая последовательность - Определение: если по Некоторому закону (правилу f) каждому натуральному числу n из множества N поставлено в соответствие число то говорят о числовой последовательности. В терминах теории множеств – множество натуральных чисел N отображается во множество чисел последовательности an. Майер И. И. 6

1. 3. Классификация функций. Свойства 1. Функция, заданная формулой, может быть явной (y = x 3 -2 x+3) или неявной (x 2 + y -25 =0) 2. Явно заданные функции подразделяются на: элементарные(с конечным количеством алгебраических операций и вычисления функций от функций) и неэлементарные. Элементарные функции подразделяются на: - стандартные : х2, sin(x) ln (x) и др; - полученные при помощи конечного количества алгебраических операций; - полученные как функция от функции (сложная функция, композиция функций, функция от функции), например, y= sin (x 2 + 2) 3. По количеству независимых аргументов – функции одного или нескольких переменных Майер И. И. 7

1. 3. Основные свойства функций 1. Четность (нечетность). Функция: - четная, если f(x) =f(-x) ; - нечетная, если f(x) = - f(-x) - общего вида, не четная и не нечетная 2. Периодичность. Для периодической функции верно f(x+T) = f(x). Здесь Т - период 3. Ограниченность. Функция ограничена на промежутке Х, если существует такое М >0, что abs(f(x)) < = М 4. Монотонность. Функция называется монотонной, если она возрастающая (f(x 2) > f(x 1) при x 2 > x 1) или убывающая (f(x 2) < f(x 1) при x 2 > x 1) 5. Непрерывность. Функция непрерывна в точке х0, если: 1. Определена в точке х0 2. Имеет конечный предел при х стремящемся к х 0 3. Этот предел равен значению функции в точке х0 Непрерывность функции - одно из важнейших ее свойств Майер И. И. 8

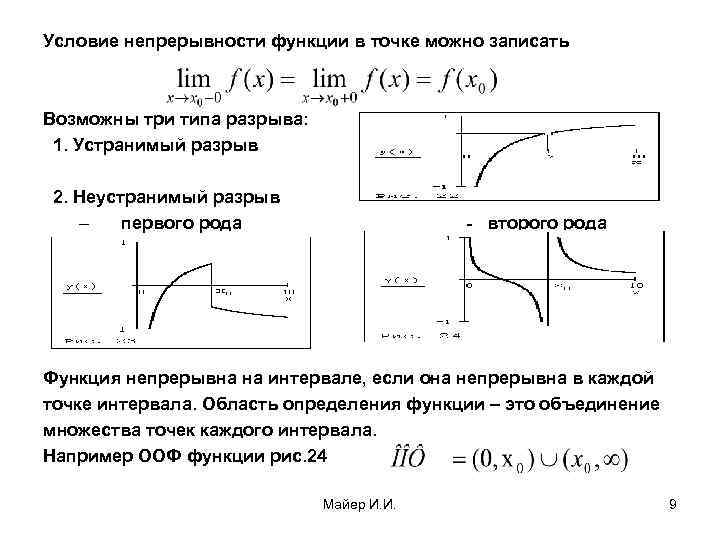Условие непрерывности функции в точке можно записать Возможны три типа разрыва: 1. Устранимый разрыв 2. Неустранимый разрыв – первого рода - второго рода Функция непрерывна на интервале, если она непрерывна в каждой точке интервала. Область определения функции – это объединение множества точек каждого интервала. Например ООФ функции рис. 24 Майер И. И. 9

1. 3. Классификация функций. Обратная функция Взаимно- однозначное соответствие, взаимно- однозначное отображение двух множеств - когда каждому элементу множества Х соответствует один элемент множества Y и при этом каждому элементу множества Y соответствует один элемент множества X Обратная функция: Если два множества Х и Y являются взаимно-обратными, то то говорят о существовании обратной функции. Записывают это так : f: Y X ; x = f-1 (Y) Инвариантность переменных позволяют записать y = f-1 (x) Примеры взаимно-обратных функций Прямая функция Обратная функция Майер И. И. 10

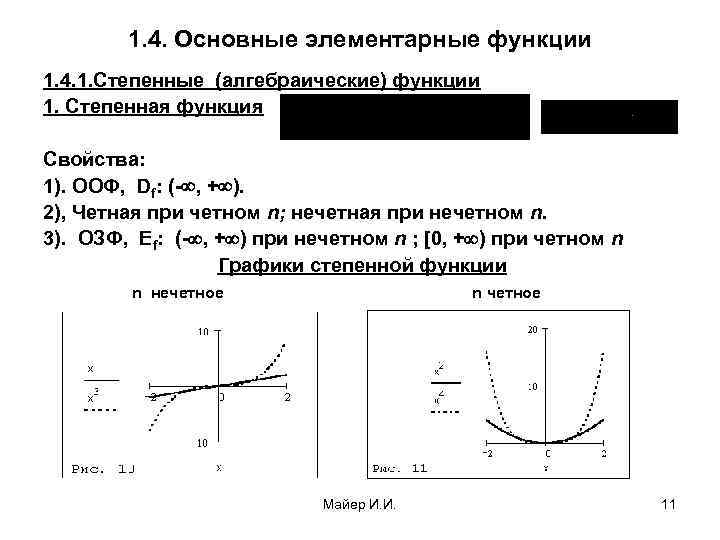1. 4. Основные элементарные функции 1. 4. 1. Степенные (алгебраические) функции 1. Степенная функция Свойства: 1). ООФ, Df: (- , + ). 2), Четная при четном n; нечетная при нечетном n. 3). ОЗФ, Ef: (- , + ) при нечетном n ; [0, + ) при четном n Графики степенной функции n нечетное n четное Майер И. И. 11

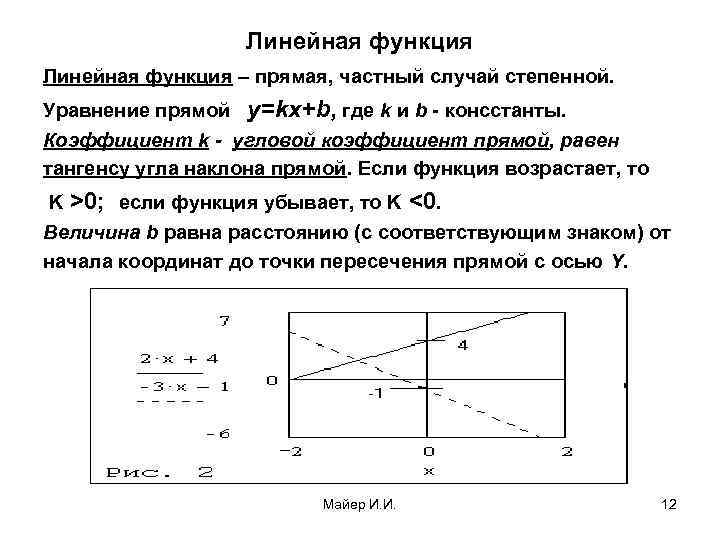Линейная функция – прямая, частный случай степенной. Уравнение прямой y=kx+b, где k и b - консстанты. Коэффициент k - угловой коэффициент прямой, равен тангенсу угла наклона прямой. Если функция возрастает, то K >0; если функция убывает, то K <0. Величина b равна расстоянию (с соответствующим знаком) от начала координат до точки пересечения прямой с осью Y. Майер И. И. 12

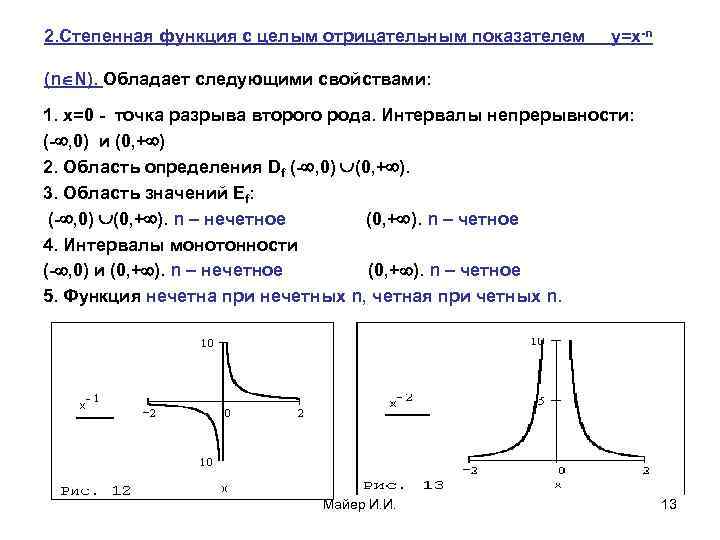2. Степенная функция с целым отрицательным показателем y=x-n (n N). Обладает следующими свойствами: 1. x=0 - точка разрыва второго рода. Интервалы непрерывности: (- , 0) и (0, + ) 2. Область определения Df (- , 0) (0, + ). 3. Область значений Ef: (- , 0) (0, + ). n – нечетное (0, + ). n – четное 4. Интервалы монотонности (- , 0) и (0, + ). n – нечетное (0, + ). n – четное 5. Функция нечетна при нечетных n, четная при четных n. Майер И. И. 13

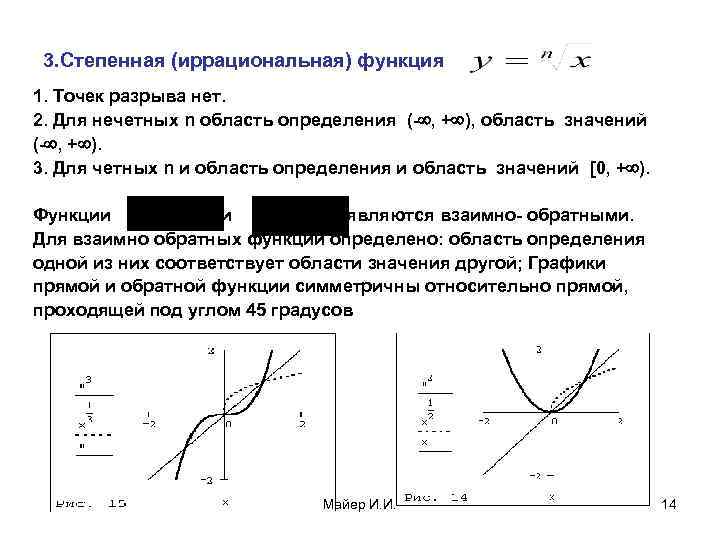3. Степенная (иррациональная) функция 1. Точек разрыва нет. 2. Для нечетных n область определения (- , + ), область значений (- , + ). 3. Для четных n и область определения и область значений [0, + ). Функции и являются взаимно- обратными. Для взаимно обратных функций определено: область определения одной из них соответствует области значения другой; Графики прямой и обратной функции симметричны относительно прямой, проходящей под углом 45 градусов Майер И. И. 14

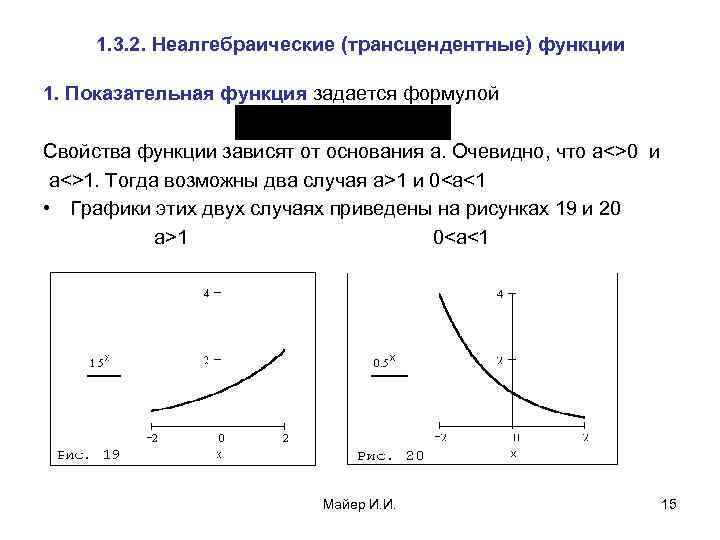1. 3. 2. Неалгебраические (трансцендентные) функции 1. Показательная функция задается формулой Свойства функции зависят от основания a. Очевидно, что a<>0 и a<>1. Тогда возможны два случая a>1 и 01 0

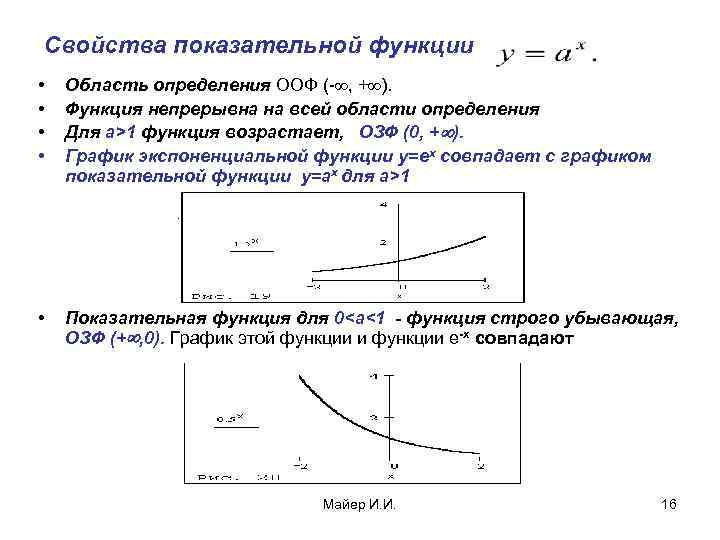Свойства показательной функции • • Область определения ООФ (- , + ). Функция непрерывна на всей области определения Для а>1 функция возрастает, ОЗФ (0, + ). График экспоненциальной функции y=ex совпадает с графиком показательной функции y=ax для а>1 • Показательная функция для 0

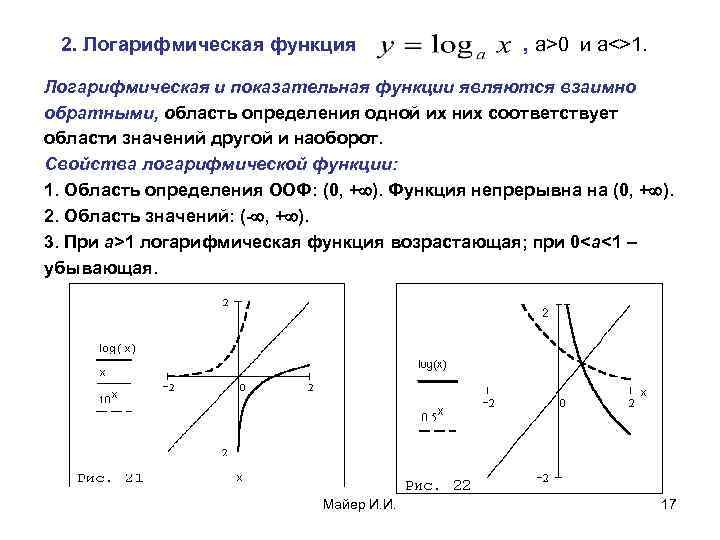2. Логарифмическая функция , a>0 и a<>1. Логарифмическая и показательная функции являются взаимно обратными, область определения одной их них соответствует области значений другой и наоборот. Свойства логарифмической функции: 1. Область определения ООФ: (0, + ). Функция непрерывна на (0, + ). 2. Область значений: (- , + ). 3. При a>1 логарифмическая функция возрастающая; при 0

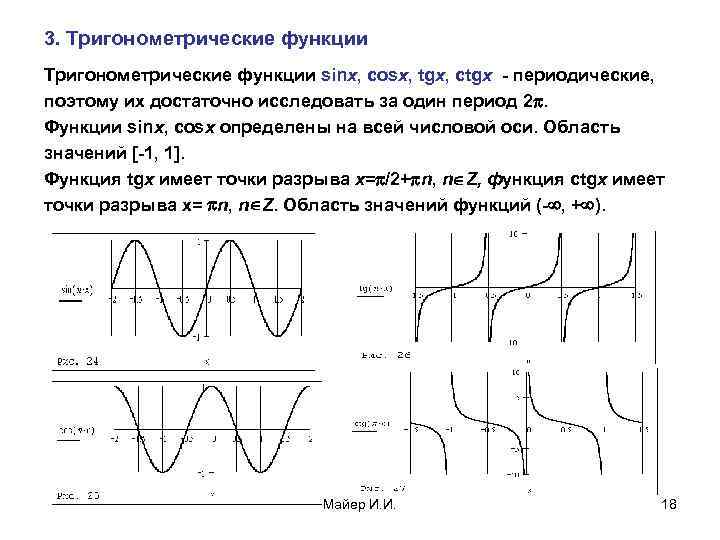3. Тригонометрические функции sinx, cosx, tgx, ctgx - периодические, поэтому их достаточно исследовать за один период 2. Функции sinx, cosx определены на всей числовой оси. Область значений [-1, 1]. Функция tgx имеет точки разрыва x= /2+ n, n Z, функция ctgx имеет точки разрыва х= n, n Z. Область значений функций (- , + ). Майер И. И. 18

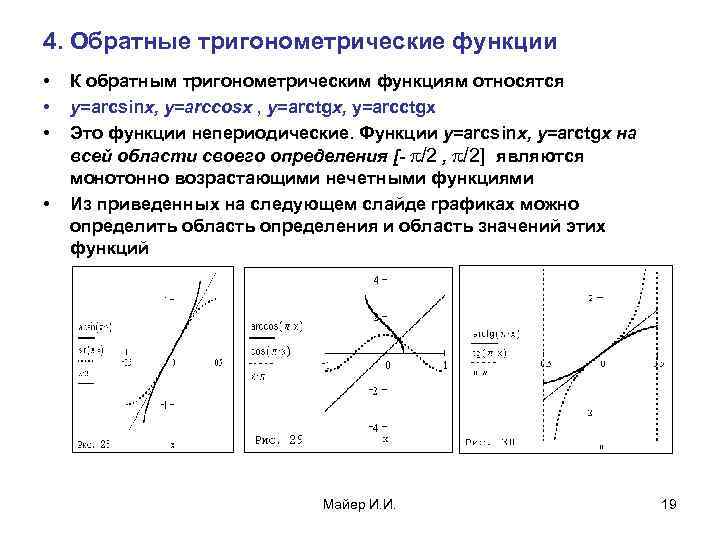4. Обратные тригонометрические функции • • К обратным тригонометрическим функциям относятся y=arcsinx, y=arccosx , y=arctgx, y=arcсtgx Это функции непериодические. Функции y=arcsinx, y=arctgx на всей области своего определения [- /2 , /2] являются монотонно возрастающими нечетными функциями Из приведенных на следующем слайде графиках можно определить область определения и область значений этих функций Майер И. И. 19

1. 4. Числовые последовательности • Фундаментальное свойство отображение позволяет определить как числовую функцию , так и числовую последовательность • Если по некоторому закону (правилу f) каждому натуральному числу n из множества N поставлено в соответствие число • то говорят о числовой последовательности. В терминах теории множеств – множество натуральных чисел N отображается во множество чисел последовательности an. • К числовым последовательностям относят: Ш Арифметическую прогрессию Ш Геометрическую прогрессию Ш Последовательности, элементы которых вычисляются по некоторому правилу f, Майер И. И. 20

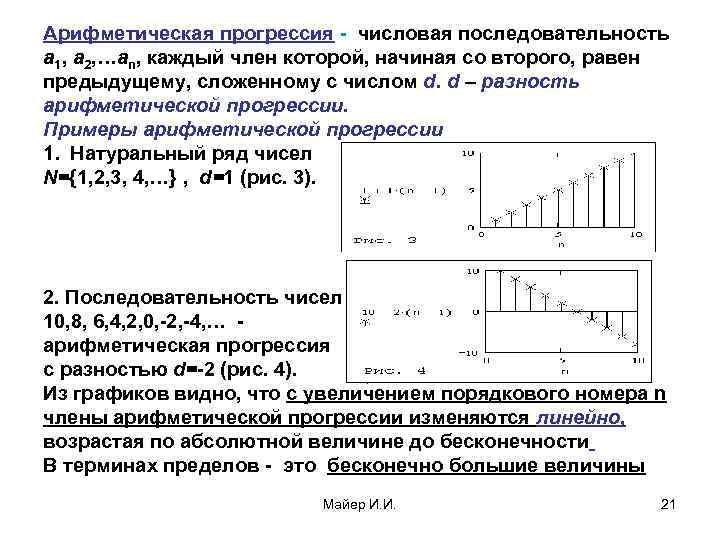Арифметическая прогрессия - числовая последовательность a 1, a 2, …an, каждый член которой, начиная со второго, равен предыдущему, сложенному с числом d. d – разность арифметической прогрессии. Примеры арифметической прогрессии 1. Натуральный ряд чисел N={1, 2, 3, 4, …} , d=1 (рис. 3). 2. Последовательность чисел 10, 8, 6, 4, 2, 0, -2, -4, … арифметическая прогрессия с разностью d=-2 (рис. 4). Из графиков видно, что с увеличением порядкового номера n члены арифметической прогрессии изменяются линейно, возрастая по абсолютной величине до бесконечности В терминах пределов - это бесконечно большие величины Майер И. И. 21

Числа 5, 10, 20, 40, … со знаменателем q=2 образуют возрастающую геометрическую прогрессию (рис. 5). Числа 0. 1, 0. 001, …со знаменателем q=0. 1 образуют убывающую геометрическую прогрессию (рис. 6). Числа 3, -6, 12, -24, … образуют знакопеременную геометрическую прогрессию со знаменателем q = - 2 (рис. 7). Вывод: из графиков следует, что с ростом n члены геометрической прогрессии изменяются нелинейно Майер И. И. 22

1. 5. Предел: числовой последовательности; числовой функции Величина А называется: - пределом числовой последовательности, если для любой сколь угодно малой величины найдется такой номер n, что абсолютная разность между членом последовательности an и величиной А меньше. Предел последовательности – величина которой стремится an. В предельном плане различают: - Бесконечно большие последовательности, ББП - Бесконечно малые последовательности , БМП - Ограниченные последовательности Майер И. И. 23

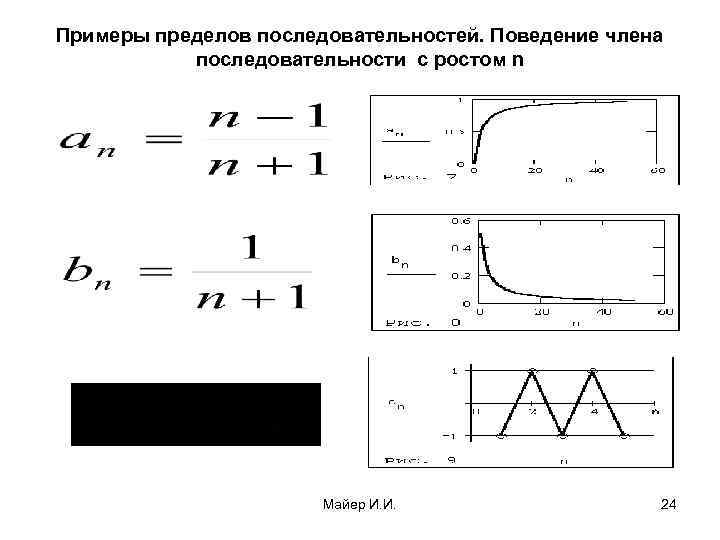Примеры пределов последовательностей. Поведение члена последовательности с ростом n Майер И. И. 24

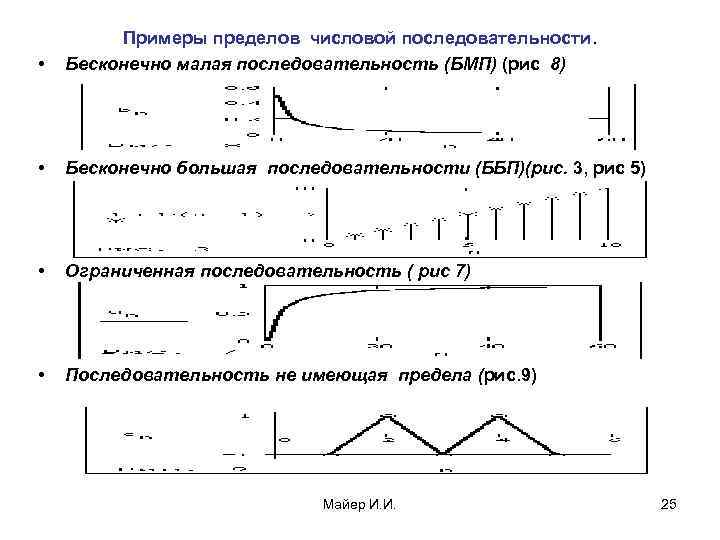• Примеры пределов числовой последовательности. Бесконечно малая последовательность (БМП) (рис 8) • Бесконечно большая последовательности (ББП)(рис. 3, рис 5) • Ограниченная последовательность ( рис 7) • Последовательность не имеющая предела (рис. 9) Майер И. И. 25

1. 6. Предел функции. Число А называется пределом числовой функции, если для любой сколь угодно малой величины всегда найдется такое, зависящее от положительное число S > 0, что для всех х , для которых верно abs(x) >S верно неравенство • A < f(x) < A+ При исследовании функции рассматривают пределы : - на границах области определения, чаще это интервал (- , + ) - в точке. При этом рассматриваются: предел слева от точки ( левосторонний предел ); предел справа от точки (правосторонний предел) ; предел функции в точке Условие непрерывности функции в точке: левосторонний предел конечен, равен правостороннему и равен значению функции в точке Майер И. И. 26

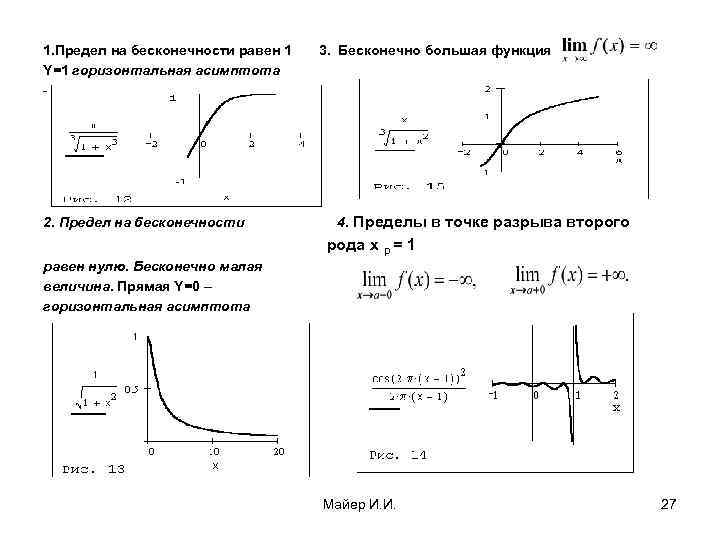1. Предел на бесконечности равен 1 Y=1 горизонтальная асимптота - 2. Предел на бесконечности 3. Бесконечно большая функция 4. Пределы в точке разрыва второго рода х р = 1 равен нулю. Бесконечно малая величина. Прямая Y=0 – горизонтальная асимптота Майер И. И. 27

Основные свойства пределов 1. Предел постоянной величины есть сама постоянная 2. Предел алгебраической суммы величин равен алгебраической сумме пределов этих величин 3. Предел произведения величин равен произведению пределов 4. Предел отношения двух величин равен отношению пределов, при условии, что предел знаменателя отличен от нуля • если 5. Предел сложной функции равен пределу от предела lim f (u (x) ) = lim f (lim (u (x) ) Майер И. И. 28

1. 7. Методы вычисления пределов функции Пример 1. Найти предел при Предел числителя и предел знаменателя равны , поэтому получается неопределенность типа Майер И. И. 29

1. 7. Методы вычисления пределов функции Пример 1. Найти предел при Разделим числитель и знаменатель на старшую степень знаменателя Получим Майер И. И. 30

1. 7. Примеры вычисления пределов функции • Пример 2. Найти • Получили неопределенность • Разделим числитель и знаменатель на • Предел числителя в полученной дроби равен 4, а предел знаменателя равен нулю. Следовательно, Майер И. И. 31

Приведенные примеры приводит к общему правилу вычисления предела отношения двух многочленов при раскрытии неопределенности типа Запишем задачу в общем виде Здесь n, m - старшие степени при х числителя и знаменателя соответственно Майер И. И. 32

1. 7. Методы вычисления пределов Предел сложной функции, функции от функции Y=f(U(x)) Правило вычисления предела: lim f(U(x))= lim f (lim U(x) ) Пример 4. Вычислить = Пример 5. Вычислить = Некоторые задачи этого класса приводят ко второму замечательному пределу и его свойствам Майер И. И. 33

Замечательные пределы В прикладных задачах радиотехники, физики широкое применение получил первый замечательный предел и его следствия В банковской деятельности, для анализа доходности по сложной схеме начисления процентов применяется второй замечательный предел • и его следствия Здесь е – константа Эйлера; е = 2. 73 Майер И. И. 34

Применение второго замечательного предела Пример 6. Вычислить Введем новую переменную t=x-2. Тогда x=t+2 и Результат получен с учетом того, что Майер И. И. 35

Пример 7. Вычислить Решение. Преобразуем выражение Обозначим t=2 x-1. Получим Майер И. И. 36

Практическое применение второго замечательного предела Эффективность финансовой операции зависит не только от ставки процента, но и от продолжительности самой операции. Принято оперировать с так называемой «годовой ставкой процента» , когда базовый период равен одному году, а расчет ставки процента любой продолжительности выполняют по различным схемам. Самой эффективной является схема сложных процентов, с разбивкой года на периоды начисления: ежеквартальный, ежемесячный и т. д. Принятые обозначения: р% - годовая процентная в процентах i = р%/ 100 – годовая ставка начислений к - количество периодов начисления t – период начисления S(0) – начальная сумма S(t) – сумма в момент времени t, начисленная сумма Формула сложных процентов за t целых лет: S(t) = S(0)*(1+i)t Формула сложных процентов за к периодов в течении одного года : S(t) = S(0)*(1+i/к)к Майер И. И. 37

Решим предельную задачу : во сколько раз увеличится к концу года первоначальный вклад, если число периодов начисления процентов k будет неограниченно возрастать? Применив второй замечательный предел, получим, что при годовой процентной ставке p =100 % даст приращение первоначального капитала в e раз, т. е. менее, чем втрое Майер И. И. 38

Примеры вычисления пределов с учетом иерархии Иерархия последовательностей (функций) по скорости возрастания (или убывания) при n ->∞ (x->∞) -для последовательностей , n->∞: n!>>en >>na>>ln(n) где a > 0 -для функций: при x-> ∞ ex >> xa>> ln(x) – где a > 0. Майер И. И. 39

Вычисление пределов с учетом иерархии Пример 8. Вычислить Получили неопределенность . Чтобы избавиться от неопределенности, необходимо преобразовать исходную формулу С учетом иерархии ex >> xa получим Майер И. И. 40

Примеры вычисления пределов дробно-рациональной функции Пример др. 1. (n< m) Пример др2. (n=m) Пример др3. (n>m) Пример др4. (n>m) Знак минус в примере др4. получен, так как у коэффициентов при старших степенях числителя и знаменателя разные знаки Майер И. И. 41