Тема 1. ОСНОВИ СТАНДАРТИЗАЦІЇ І МЕТРОЛОГІЇ Лекція 2.

Тема 1. ОСНОВИ СТАНДАРТИЗАЦІЇ І МЕТРОЛОГІЇ Лекція 2. Методи та похибки вимірювань

Питання лекції: 1.Похибки засобів вимірювання. 2. Оформлення результатів вимірювання. 3.Систематичні похибки, способи виявлення і зменшення впливу. 4.Випадкові похибки. Література: Л1 с.19…31; Л2 с.32…40. Матеріально –технічне забезпечення: ПЕОМ, проектор, слайди.

Мета лекції Розглянути: особливості розрахунку оцінок результатів вимірювання при прямих та непрямих методах вимірювання; способи знаходження та зменшення впливу систематичних похибок; знаходження оцінок випадкових похибок.

1. Похибки засобів вимірювання Клас точності ЗВТ(ЗВ) – узагальнена характеристика, що визначається межами його допустимих основних і додаткових похибок, а також іншими характеристиками, що впливають на його точність, значення яких регламентується. 1.1. Нормується межа абсолютної похибки  =  а – якщо значення похибки залишається практично постійним у діапазоні вимірювань;  =  (а + bХ) – якщо значення похибки можна вважати таким, що змінюється за лінійним законом,

1.2. Нормується межа відносної похибки Якщо межі відносної похибки практично незмінні, то межі допустимої основної відносної похибки встановлюються за виразом де q – позитивне число, що обирається із стандартизованого ряду (1; 1,5; 2; 2,5; 3; 4; 5; 6) 10n; n = 1; 0;-1; -2. (1) Якщо ж межі абсолютних похибок змінюються практично лінійно, то межі допустимої відносної основної похибки встановлюють за виразом де с і d – позитивні числа, що обираються з ряду (1), – кінцева межа вимірювання.

1.3. Нормується межа зведеної похибки Межі допустимої зведеної похибки, встановлюються за формулою де Р – позитивне число, що обирається із ряду (1). У цьому випадку клас точності позначають числами, які дорівнюють межам припущеної зведеної похибки, вираженими в процентах. При цьому можливі такі два випадки позначення класу точності: 1. Якщо нормуюче значення виражене у одиницях вимірюваної величини, то клас точності позначається просто числом, наприклад 2,5. 2. Якщо нормуюче значення виражене довжиною робочої ділянки шкали, тоді під числом, що позначає клас точності, ставиться позначка у вигляді кута.

2. Принципи опису й оцінювання похибок, запис результатів вимірювання. Стандартом встановлено, що в чисельних показниках точності вимірювань (у тому числі й у похибці) повинно бути не більше двох значимих цифр, причому дві цифри утримуються в таких випадках: при особливо відповідальних і точних вимірюваннях; якщо числова величина двох значимих цифр менше 30; якщо з одержаними результатами передбачається проводити подальші розрахунки. В інших випадках утримується одна значима цифра. При записі результатів вимірювань найменші розряди числових значень результату вимірювання і чисельних показників точності повинні бути однакові.

Правила округлення результатів і похибок вимірювань: 1. Зайві цифри, які мають розряди менші розряду похибки, в цілих числах замінюються нулями, а в десятинних дробах відкидаються. При цьому в запису цілого числа, як правило, ці нулі не виписуються, а щоб число залишилось без зміни, застосовують множення на 10 у відповідній степені. 2. Якщо в групі цифр, які відкидаються або замінюються нулями, цифра старшого розряду (перша зліва) менша 5, то цифри, які залишаються не змінюються. 3. Якщо в групі цифр, які відкидаються або замінюються нулями, цифра старшого розряду більша 5, а наступні цифри не нулі, то остання (справа) цифра, яка залишається, збільшується на одиницю. 4. Якщо в групі цифр, які відкидаються або замінюються нулями, цифра старшого розряду дорівнює 5, а за нею немає цифр або йдуть нулі, то закруглення проводиться до найближчої парної цифри, тобто якщо остання цифра в закругленому числі парна або нуль, то вона залишається без зміни, якщо ж вона не парна то збільшується на одиницю.

Оцінка прямих одноразових вимірювань Для технічних вимірювань встановлюється така форма представлення результатів вимірювання А;  від н до в; Р, де А – результат вимірювання;  – похибка вимірювання; н – нижня межа похибки; в – верхня межа похибки; Р – встановлена (довірча) ймовірність, з якою похибка знаходиться в цих межах. Для одноразових вимірювань робочими приладами Р=0,95. Допускається при симетричній довірчій похибці результат вимірювання записувати в формі А; ; Р.

Оцінка непрямих вимірювань Оцінка непрямих (опосередкованих) вимірювань: приклад – вимірювання потужності амперметром та вольтметром. Якщо Хі розложити у ряд Тейлора зберігаючи при цьому члени з нульовими і першими степенями погрішностей , то можна отримати де – часткові похибки. Таким чином, похибка результату непрямого вимірювання залежить не тільки від похибок прямих вимірювань, але і від вигляду функціональної залежності.

Види функціональної залежності 1. Вимірювана величина є функцією одного параметра. тоді де а – постійний множник; – результат прямого вимірювання величини X; Х – абсолютна похибка прямого вимірювання. 2. Вимірювана величина є функцією суми або різниці двох параметрів 3. Вимірювана величина є добутком декількох параметрів де – відносні похибки вимірювань параметрів в Х1 … Хn.

3. Систематичні похибки, способи виявлення і зменшення впливу. Залежно від джерела виникнення похибки поділяються на: а) методичні похибки (недосконалість методів вимірювань, припущення, спрощення, невідповідність об’єкта вимірювань теоретичній моделі тощо). Методична похибка є систематичною; б) інструментальні похибки (властивості засобів вимірювань, пов’язані з принципом їх дії, конструкційними та технічними обмеженнями); в) суб’єктивні, або особисті похибки (зумовлені особливостями індивідуальних властивостей людини); г) зовнішні похибки (виникають внаслідок впливу зовнішніх умов – електричних і магнітних полів, атмосферного тиску, вологи тощо).

Стандартні ситуації щодо систематичних похибок 1. Умови вимірювання дозволяють вилучити джерело систематичної похибки до вимірювання. 2. Вилучити систематичну похибку не можна, (але її походження відоме і вона може бути досить точно оцінена (розрахунком, додатковим експериментом). В таких випадках уводять поправку. 3. Причина систематичної похибки відома, але її значення невідоме, є тільки відомості про межі похибки. В таких випадках зменшити її вплив дозволяє метод рандомізації, тобто переведення систематичної похибки у випадкову, а потім статистична обробка результатів вимірювання. 4. Систематична похибка існує, але про неї нічого не відомо, що може привести в результаті вимірювань до помилкових висновків. У цьому випадку проводять вимірювання різними методами, різними приладами, в різних умовах, а потім проводять сумісну обробку результатів спостережень.

Рекомендації щодо зменшення впливу систематичних похибок на етапі підготовки до проведення вимірювань: 1. Правильно вибирати прилади і методи вимірювань. 2. Сумлінно готувати прилади до роботи (виставляти нулі, калібрувати, прогрівати). 3. Виконувати вимоги метрологічного забезпечення щодо своєчасної повірки ЗВТ, в разі сумнівів направляти прилади на позачергову повірку. 4. Застосовувати індивідуальні засоби передбачені комплектуванням приладу (калібровані провідники, дільники тощо). 5. Правильно розміщувати прилади (робоче положення, взаємне розміщення), при необхідності застосовувати екранізацію або термостатування приладів.

Методи виявлення і вилучення систематичних похибок на етапі проведення вимірювання 1. Заміщення, при якому вимірювана величина заміщується зразковою мірою. 2. Компенсація за знаком, при якому вимірювання проводять двічі так, щоб невідома за абсолютним значенням, але відома за своєю природою систематична похибка входила до результатів спостережень з протилежними знаками Х1=Х+Хсп, а Х2=Х-Хсп, тоді значення величини Х=(Х1+Х2)/2. 3. Рандомізація. На етапі обробки результатів вводять поправки або поправочні множники (аналітичне вилучення систематичних похибок).

4. Випадкові похибки Якщо систематичні похибки виключені з результатів вимірювань, а функція розподілу ймовірностей має симетричний характер, то послідовність розрахунків оцінок буде такою: 1. Розраховують середнє арифметичне результатів n спостережень, яке приймають за результат вимірювання

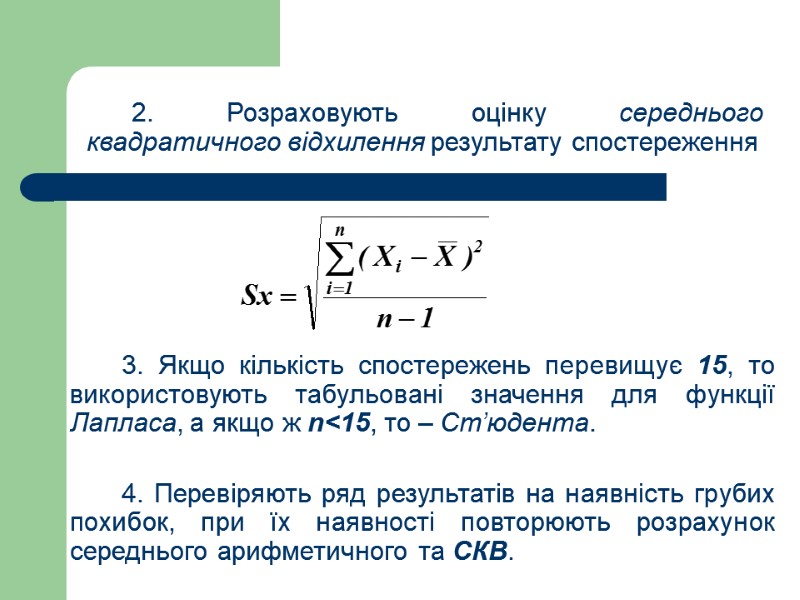
2. Розраховують оцінку середнього квадратичного відхилення результату спостереження 3. Якщо кількість спостережень перевищує 15, то використовують табульовані значення для функції Лапласа, а якщо ж n<15, то – Ст’юдента. 4. Перевіряють ряд результатів на наявність грубих похибок, при їх наявності повторюють розрахунок середнього арифметичного та СКВ.

5. Обчислюють оцінку СКВ результату вимірювання 6. Для конкретного закону розподілу результатів спостережень обчислюють довірчі границі випадкової похибки результату вимірювання. 7. Записують результат вимірювання у вигляді де  -- границя похибки результату вимірювання; РД – довірча ймовірність.

Висновки: 1. Точність вимірювання, окрім інших факторів, залежить від класу точності ЗВТ (ЗВ). 2. Результати вимірювань та їх оцінка мають спеціальні форми запису, що визначаються відповідними нормативними документами. 3. Знання джерел систематичних похибок надає шляхи і методи їх знаходження, зменшення впливу або взагалі, їх усунення. 4. Для точного розрахунку оцінок результатів вимірювань потрібно використовувати спеціально розроблені методики.