1. Мат_модель проблемной ситуации.ppt
- Количество слайдов: 13

Тема 1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОБЛЕМНОЙ СИТУАЦИИ

o o Решение современных экономических задач и анализ экономической ситуации невозможен без использования математических моделей и методов. Специфика предмета, его методологическая особенность заключается в том, что изучаются не сами экономические объекты и явления как таковые, а их математические модели. Математической моделью реального объекта (явления) называется ее упрощенная, идеализированная схема, составленная с помощью математических символов и операций (соотношений). Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта.

o o Простейшие математические модели на уровне таблиц и формул использовались еще Ф. Кене в 1758 г. в работе «Экономические таблицы» , А. Смитом для описания макроэкономической модели, Д. Риккардо в описании модели международной торговли. В XX в. значительный вклад в развитие экономикоматематических моделей внесли такие ученые как: В. В. Леонтьев, Дж. Хикс, П. Самуэльсон, Л. В. Канторович, Р. Беллман и др. Развитие эк. мат. моделирования в России

o Единой классификации экономикоматематических моделей не существует, хотя можно выделить наиболее значимые их группы в зависимости от признака классификации. Классификация ЭММ o Экономико-математическая модель имеет ряд обязательных свойств. Свойства ЭММ

o o o Разработка новой модели – это сложный творческий процесс, требующий больших умственных и временных затрат. Для экономии этих ресурсов полезно обращаться к существующему "банку" моделей для проверки пригодности их к новой задаче. Можно привести следующую схему выбора модели и метода ее исследования (рис. 1).
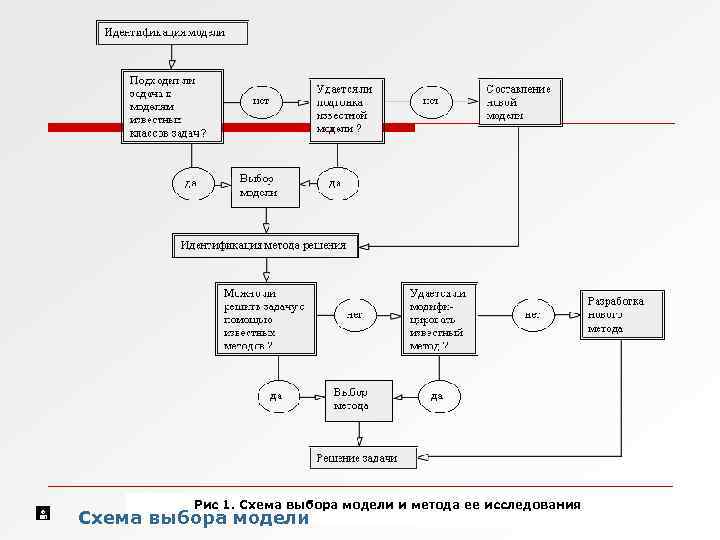
Рис 1. Схема выбора модели и метода ее исследования Схема выбора модели

o Экономико-математические модели являются продуктом процесса экономикоматематического моделирования. o Экономико-математическое моделирование (формализация) – это описание существенных свойств и черт изучаемого экономического объекта на языке математических символов и соотношений. Другими словами, вся совокупность действий, связанных с построением, анализом и другими операциями, проводимыми с моделями, называется экономико-математическим моделированием. o

o o Можно выделить три этапа проведения экономикоматематического моделирования. На первом этапе ставятся цели и задачи исследования, проводится качественное описание объекта в виде экономической модели. На втором этапе формируется математическая модель изучаемого объекта, осуществляется выбор (или разработка) методов исследования, проводится программирование модели на ЭВМ, подготавливается исходная информация. Далее проводится пригодность машинной модели на основании правильности получаемых с ее помощью результатов и оценка их устойчивости. На третьем, основном этапе экономико-математического моделирования осуществляется анализ математической модели, реализованной в виде программ для ЭВМ, проведение машинных расчетов, обработка и анализ полученных результатов.

o o Инструментом для осуществления процесса экономико-математического моделирования являются экономико-математические методы. Экономико-математические методы представляют собой комплекс экономикоматематических дисциплин, объединенных для изучения социально-экономических систем и процессов.

Самым крупным разделом в составе экономикоматематических методов выступают методы принятия оптимальных решений (в том числе и исследование операций), которые включают в себя следующие дисциплины и методы: o оптимальное (математическое) программирование; o сетевые методы планирования и управления; o теорию и методы управления запасами; o теорию игр; o теорию массового обслуживания; o теорию расписания и др.

o o o Оптимизация (от лат. optimum – наилучшее), процесс нахождения экстремума (глобального максимума или минимума) определённой функции или выбора наилучшего (оптимального) варианта из множества возможных. Математическое программирование (термин "программирование" имеет смысл "планирования", "сравнения вариантов", "оптимизации") занимается решением экстремальных задач (оптимизационных задачам). Суть решения таких задач состоит в отыскании максимального или минимального значения заданной функции (целевой функции или объективной функции или критерий эффективности) на заданном множестве значений ее аргументов (множества допустимых решений). Причем, множество допустимых решений задается (описывается) с помощью некоторых уравнений или неравенств.

Традиционно в математическом программировании выделяют следующие основные разделы: 1. Линейное программирование – целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств. В свою очередь в линейном программировании существуют классы задач, структура которых позволяет создать специальные методы их решения, выгодно отличающиеся от методов решения задач общего характера. Так, в линейном программировании появился раздел транспортных задач. 2. Нелинейное программирование – целевая функция и (или) система ограничений задаются нелинейными функциями. Нелинейное программирование принято подразделять на: o выпуклое программирование; o квадратичное программирование; o многоэкстремальные задачи.

3. Динамическое программирование – задачи, в которых имеется переменная времени и целевая функция выражается не в явном виде как функция переменных, а косвенно – через уравнения, описывающие протекание операций во времени. Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно-линейного программирования. o В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения. o В задачах параметрического программирования целевая функция или функция, определяющая область возможных изменений переменных, либо то и другое зависят от некоторых параметров. o В задачах дробно-линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, также являются линейными. o Также выделяют задачи стохастического, эвристического, геометрического программирования. o
1. Мат_модель проблемной ситуации.ppt