Тела вращения Телом вращения в простейшем случае

Тела вращения

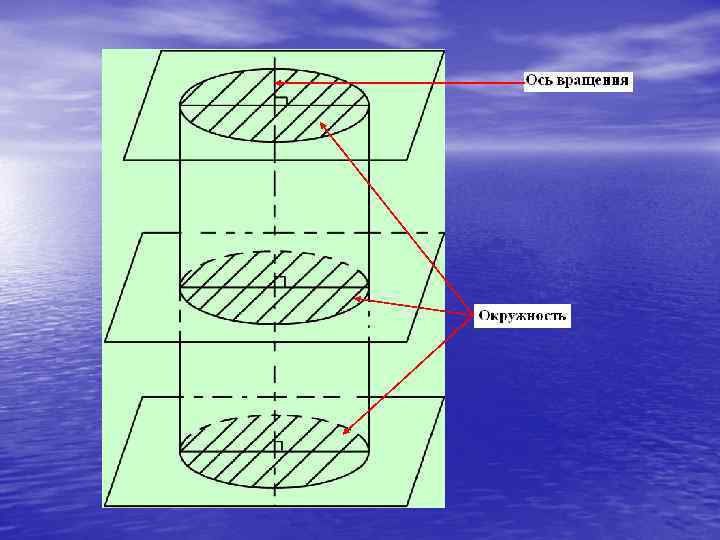
Телом вращения в простейшем случае называется такое тело, которое плоскостями, перпендикулярными некоторой оси (оси вращения), пересекается по кругам с центрами на этой прямой. Прямой цилиндр, конус, шар являются примерами тел вращения. Т. е. как видно из определения в любом теле вращения должно быть: Ø Ось вращения Ø Все плоскости, проходящие через тело и перпендикулярные оси вращения, при пересечен с телом должны давать окружности, с центрами лежащими на этой оси. Рассмотрим одно из тел вращения – прямой цилиндр.

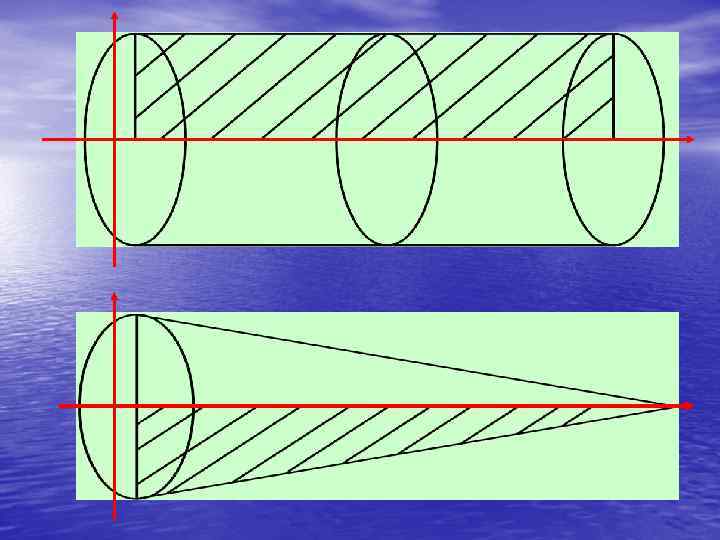
Вычисление объема тела вращения • Пусть задано тело объемом V причем имеется такая прямая , что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадь S сечения тела этой плоскостью. Но плоскость, перпендикулярная оси Ох, пересекает ее в некоторой точке х. Следовательно, каждому числу x из отрезка [а; b] поставлено в соответствие единственное число S(x) — площадь сечения тела этой плоскостью. Тем самым на отрезке [а; b] задана функция S(x). Если функция S непрерывна на отрезке [а; b] то справедлива формула (1)

Если же тело образовано вращением вокруг оси Ox криволинейной трапеции a. ABb, ограниченной сверху дугой непрерывной линии y=ƒ(x), где a≤ x ≤ b, то: и формула (1) примет вид: : формула для вычисления объема тела вращения

Таким образом, для того, чтобы найти объем тела вращения, нам необходимо знать уравнение непрерывной функции, график которой ограничивает сверху криволинейную трапецию, вращением которой вокруг оси и получается данное тело. Рассмотрим пример: Вычислить объем тела, образованного вращением вокруг оси Ox сегмента параболы отсеченного прямой x = 3. Решение. Функция является непрерывной на данном отрезке. Пределы интегрирования здесь даны непосредственно, и сразу же по формуле можно найти искомый объем:

Площадь поверхности вращения. • Рассмотрим поверхность, полученную вращением дуги линии y = f(x) (a≤x≤b) вокруг оси Ох (предположим, что функция у = f(x) имеет непрерывную производную). Фиксируем значение x є [а, b], аргументу функции придадим приращение dx, которому соответствует «элементарное кольцо» , полученное вращением элементарной дуги ∆l. Это «кольцо» заменим цилиндрическим кольцом - боковой поверхностью тела, образованного вращением прямоугольника с основанием, равным дифференциалу дуги dl, и высотой h = f(x). Разрезав последнее кольцо и развернув его, получим полоску шириной dl и длиной 2πу, где у =f(x).

Следовательно, дифференциал площади поверхности выразится формулой: откуда формула для вычисления поверхности тела вращения Пример Вычислить площадь поверхности, полученной вращением отрезка прямой y = x (0≤x≤h) вокруг оси Ox. Решение. Поскольку a=0, b=h, то по формуле получим

Конус в переводе с греческого «konos» означает «сосновая шишка» . С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287– 212 гг. до н. э. ) «О методе» , в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470 – 380 гг. до н. э. ) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса. Вычислим объем прямого конуса, высота которого H и радиус основания R. Для этого будем рассматривать конус, как тело вращения прямоугольного треугольника около одного из катетов.

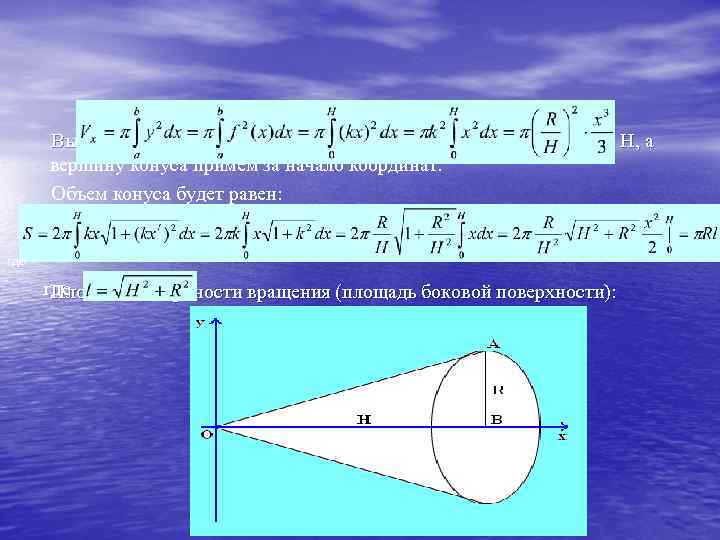Выберем систему координат так, чтобы ось Ox совпала с высотой H, а вершину конуса примем за начало координат. Объем конуса будет равен: где Площадь поверхности вращения (площадь боковой поверхности):

Вычислить объем усеченного конуса, у которого радиусы оснований R 1 и R 2 (R 2>R 1), а высота h. Составляем уравнение кривой: b=R 1, k=(R 2 -R 1)/h. Значит уравнение кривой: Тогда объем равен:

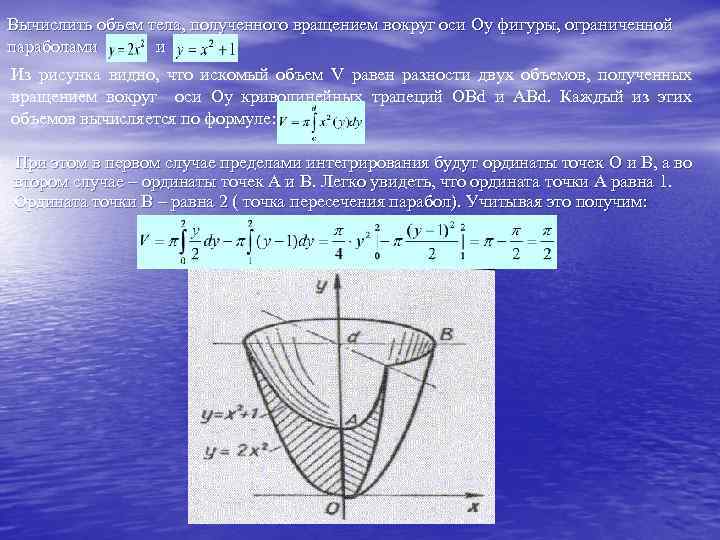Вычислить объем тела, полученного вращением вокруг оси Oy фигуры, ограниченной параболами и Из рисунка видно, что искомый объем V равен разности двух объемов, полученных вращением вокруг оси Oy криволинейных трапеций OBd и ABd. Каждый из этих объемов вычисляется по формуле: При этом в первом случае пределами интегрирования будут ординаты точек O и B, а во втором случае – ординаты точек A и B. Легко увидеть, что ордината точки А равна 1. Ордината точки B – равна 2 ( точка пересечения парабол). Учитывая это получим:

Найдите площадь поверхности шара радиуса R Решение. Поместим начало координат в центре шара. Будем рассматривать поверхность как поверхность, полученную в результате вращения полуокружности вокруг оси Ox. Тогда площадь поверхности шара найдется по формуле: Т. к. и то

Вычислить объем и площадь боковой поверхности тела, полученного вращением вокруг оси Ox фигуры, ограниченной линиями: № 1. xy=6, x=1, x=6, y=0 № 2. xy=4, x=3, x=5, y=0 № 3. № 4. y=2 x, y=x+3, x=0, x=1 № 5. y=x+2, y=1, x=0, x=2 Вычислить объем и площадь боковой поверхности прямого цилиндра, а также объем шара, шарового сегмента и шарового сектора.

Что царь однажды воинам своим Велел снести земли по горсти в кучу. И гордый холм возвысился, И царь мог с высоты с весельем озирать И дол, покрытый белыми шатрами, И море, где бежали корабли. » Это одна из немногих легенд, в которой при кажущемся правдоподобии нет и зерна правды. Докажем геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая куча земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм» . Войско в 100 000 воинов считалось очень внушительным V = 0, 2 x 100 000 = 20 000 дм 3 = 20 м 3. Угол откоса ≤ 45°, иначе земля начнет осыпаться. Возьмем угол откоса наибольшим возможным, т. е. 45°

образующей в 45 градусов. А это значит, что высота равна радиусу. Воспользовавшись формула объема, мы можем найти высоту: H≈2, 7 метра. Надо обладать очень богатым воображением, чтобы земляную кучу в 2, 7 м ( человеческих роста) назвать «гордым холмом» . Сделав расчет для меньшего угла, мы получили бы еще более скромный результат. У Аттилы было самое многочисленное войско, которое знал древний мир. Историки оценивают его в 700 000 человек. К сведению, Аттила – предводитель гуннов, кочевого народа, сложившегося в Приуралье из многих племен. Массовое передвижение гуннов на запад (с 70 -х гг. IV в. ) дало толчок «великому переселению народов» . Если бы все воины Аттилы участвовали в насыпании холма, образовалась бы куча повыше вычисленной нами, но не очень. Советую вам самим дома вычислить высоту кургана и подумать, удовлетворила бы такая высота честолюбие Аттилы были нет.

формула для вычисления объема тела вращения формула для вычисления поверхности тела вращения