Текстурный анализ Раздел 4 ТЕКСТУРНЫЙ АНАЛИЗ КРИСТАЛЛОГРАФИЧЕСКИЕ ПРОЕКЦИИ

Текстурный анализ Раздел 4 ТЕКСТУРНЫЙ АНАЛИЗ. КРИСТАЛЛОГРАФИЧЕСКИЕ ПРОЕКЦИИ

Введение Главная задача кристаллографии в физическом металловедении – точно отобразить углы между плоскостями. Существует закон постоянства углов: для всех кристаллов одного и того же вещества в одной и той же модификации углы между соответствующими плоскостями одинаковы.

Введение Цель кристаллографических проекций: удобно и точно изобразить и измерять на плоском листе бумаги угловые соотношение между плоскостями, направлениями и элементами их симметрии. С помощью кристаллографических проекций исследуют в металловедении линии скольжения, двойники, выделения новых фаз, ориентировку монокристаллов, преимущественную ориентировку зерен в поликристаллах и целый ряд других задач.

Кристаллографический комплекс В кристаллографии проектируется не кристалл, а кристаллографический комплекс, полученный от данного кристалла. Кристаллографический комплекс получается при параллельном перемещении плоскостей в пространстве до взаимного пересечения их в одной точке.

Полярный комплекс В некоторых случаях проектируется полярный комплекс, который обратен кристаллическому. Полярный комплекс получается при восстановлении из центра кристаллографического комплекса перпендикуляров ко всем плоскостям. Таким образом, в полярном комплексе плоскость заменяется её нормалью (как в обратной решетке).

Виды кристаллографических проекций Для упрощения рассмотрения кристаллографических задач - плоскости или нормали к ним проектируют на различные поверхности (плоскость, сферу), что приводит к различным кристаллографическим проекциям. В кристаллографии чаще других рассматриваются следующие проекции: 1) линейная; 2) гномоническая; 3) сферическая; 4) гномосферическая; 5) стереографическая; 6) гномостереографическая.

Линейная проекция Проектируемый объект – кристаллографический комплекс. Все плоскости и направления проектируются на плоскость, находящуюся на некотором расстоянии от центра кристаллического комплекса. Линейной проекцией плоскости Q является прямая AB, по которой проектируемая плоскость Q пересекается с плоскостью проекции Р. Линейной проекцией линии кристаллографического направления ON является точка пересечения направления с плоскостью проекции N – полюс. Линейная проекция плоскости Q и направления ON

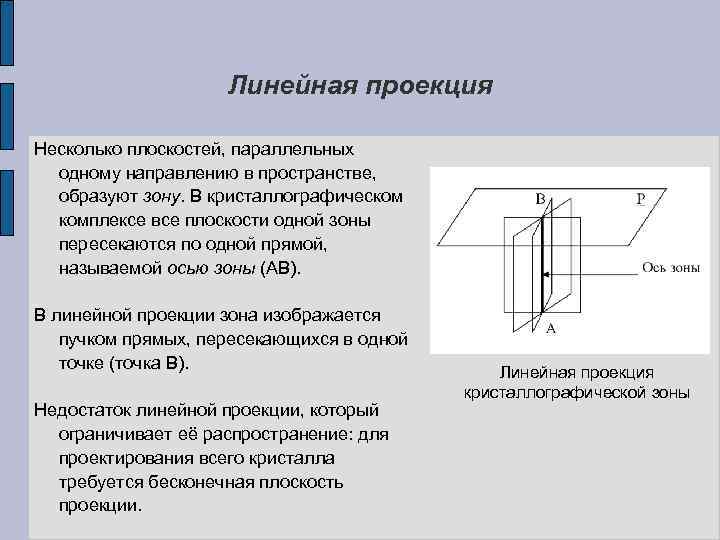Линейная проекция Несколько плоскостей, параллельных одному направлению в пространстве, образуют зону. В кристаллографическом комплексе все плоскости одной зоны пересекаются по одной прямой, называемой осью зоны (АВ). В линейной проекции зона изображается пучком прямых, пересекающихся в одной точке (точка В). Недостаток линейной проекции, который ограничивает её распространение: для проектирования всего кристалла требуется бесконечная плоскость проекции. Линейная проекция кристаллографической зоны

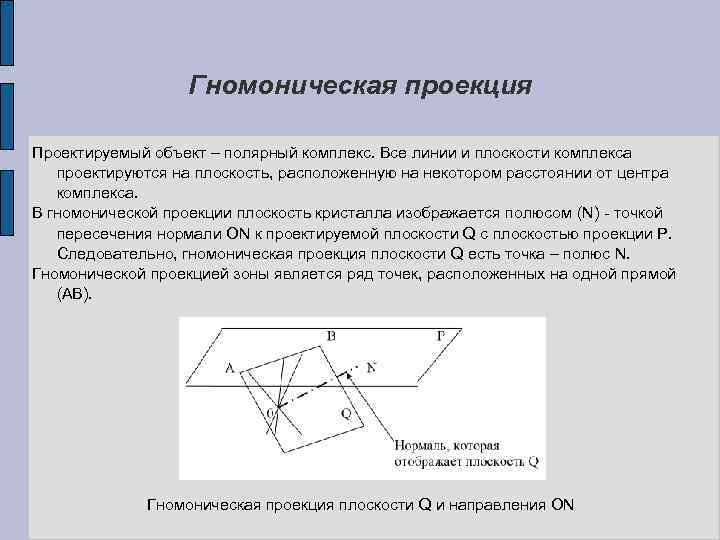Гномоническая проекция Проектируемый объект – полярный комплекс. Все линии и плоскости комплекса проектируются на плоскость, расположенную на некотором расстоянии от центра комплекса. В гномонической проекции плоскость кристалла изображается полюсом (N) - точкой пересечения нормали ON к проектируемой плоскости Q с плоскостью проекции Р. Следовательно, гномоническая проекция плоскости Q есть точка – полюс N. Гномонической проекцией зоны является ряд точек, расположенных на одной прямой (АВ). Гномоническая проекция плоскости Q и направления ON

Гномоническая проекция В полярном комплексе прямая (направление ON) отображается перпендикулярной ей плоскостью Q, поэтому гномонической проекцией направления (ON) является линия пересечения плоскости Q полярного комплекса с плоскостью проекции P, т. е. в гномонической проекции направление ON отображается линией АВ. Недостаток гномонической проекции, как и у линейной проекции, в том, что для проектирования всего кристалла требуется бесконечная плоскость. Гномоническая проекция плоскости Q и направления ON

Сферическая и гномосферическая проекции Вокруг центра кристаллографического комплекса произвольным радиусом описывается сфера, которая называется сферой проекции. Плоскости кристалла пересекают сферу по кругам наибольшего диаметра, т. е. по большим кругам. Если все плоскости проектировать подобным образом на сферу, то большие круги пересекутся под тем же углам, что и плоскости кристалла.

Сферическая и гномосферическая проекции Если в центр сферы проекций поместить полярный комплекс, то получится гномосферическая проекция, в которой кристаллографическая плоскость отображается полюсом Р – точкой пересечения перпендикуляра к плоскости с поверхностью сферы. Совокупность полюсов на сфере называется полюсной фигурой. По размещению полюсов на сфере, образующих полюсную фигуру, можно определить ориентировку кристаллографических плоскостей, т. к. угол между двумя плоскостями в кристалле равен углу между их полюсами.

Стереографическая и гномостереографическая проекции Практически более удобно пользоваться не сферой проекций, а её плоским изображением. Сфера проецируется без нарушения углов между плоскостями или полюсами.

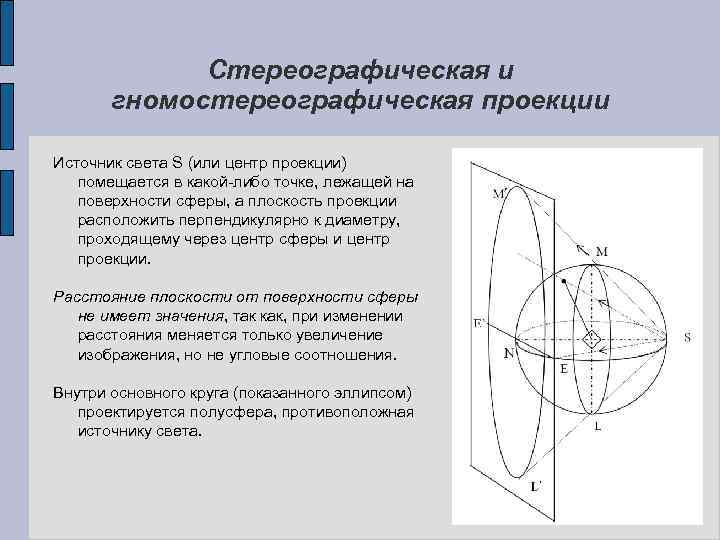Стереографическая и гномостереографическая проекции Источник света S (или центр проекции) помещается в какой-либо точке, лежащей на поверхности сферы, а плоскость проекции расположить перпендикулярно к диаметру, проходящему через центр сферы и центр проекции. Расстояние плоскости от поверхности сферы не имеет значения, так как, при изменении расстояния меняется только увеличение изображения, но не угловые соотношения. Внутри основного круга (показанного эллипсом) проектируется полусфера, противоположная источнику света.

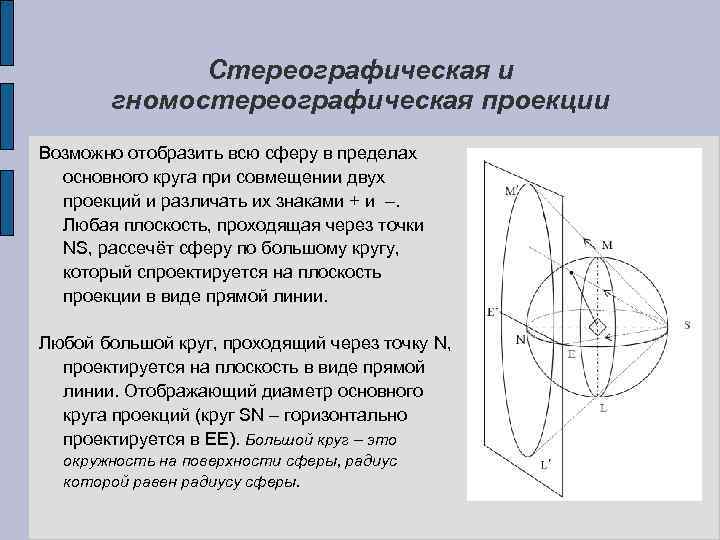Стереографическая и гномостереографическая проекции Возможно отобразить всю сферу в пределах основного круга при совмещении двух проекций и различать их знаками + и . Любая плоскость, проходящая через точки NS, рассечёт сферу по большому кругу, который спроектируется на плоскость проекции в виде прямой линии. Любой большой круг, проходящий через точку N, проектируется на плоскость в виде прямой линии. Отображающий диаметр основного круга проекций (круг SN – горизонтально проектируется в ЕЕ). Большой круг – это окружность на поверхности сферы, радиус которой равен радиусу сферы.

Стереографическая и гномостереографическая проекции Если большой горизонтальный круг разделить на градусы, то его проекция ЕЕ будет служить шкалой для стереографически спроектированных точек, лежащих на горизонтальном круге. Так же наносятся деления на вертикальный круг ML, которые проектируются на основной круг. По экватору измеряется угол в пределах 0 -1800, по основному кругу меридиану - угол в диапазоне 0 -3600 по часовой стрелке. Таким образом, можно спроектировать на плоскость глобус с линиями широты и долготы (меридианами и параллелями).

Стереографическая и гномостереографическая проекции Если ось, проходящую через северный и южный полюсы, спроектировать перпендикулярно к плоскости проекции, то стереографическая проекция всех параллелей и меридианов образует сетку Болдырева. Если ось, проходящая через северный и южный полюсы сферы, параллельна плоскости проекции, то линии долготы и широты образуют стереографическую сетку, называемую сеткой Вульфа.

Свойства стереографической и гномостереографической проекций 1. На стереографической проекции кристаллографическая плоскость, совпадающая с большим кругом, параллельным плоскости проекции, изображается основным кругом. 2. Кристаллографические плоскости, совпадающие с большим кругом, перпендикулярным плоскости проекции, проектируются в виде диаметра основного круга. 3. Наклонные плоскости изображаются в виде проекций наклонных больших кругов, которые при повороте сетки Вульфа могут совпадать с одним из меридианов.

Свойства стереографической и гномостереографической проекций 4. Кристаллографические направления на стереографической проекции изображаются в виде точек (полюсов). Поэтому стереографическая проекция плоскостей, принадлежащих одной зоне, изображаются в виде проекции кругов, пересекающихся в одной точке. 5. Гномостереографическая проекция есть проекция обратной решетки. Кристаллографические плоскости на гномостереографической проекции изображаются в виде полюсов, а кристаллографические направления в виде проекции больших кругов. Поэтому на гномостереографической проекции полюса плоскостей, принадлежащих одной зоне, лежат на проекции одного круга, который при вращении сетки можно совместить с одним из меридианов.

Свойства стереографической и гномостереографической проекций 6. Для кристаллов кубической сингонии можно пользоваться одними и теми же стандартными проекциями при изображении кристалла в стерео- или гномостереографической проекциях. Это связано с тем, что в кубической сингонии плоскости и перпендикулярные к ним направления имеют одни и те же индексы, а углы между пересекающимися плоскостями равны углам между нормалями к соответствующим плоскостям. 7. Углы между двумя точками на проекции не изменяются при вращении точек вокруг оси (центра) стереографической проекции. 8. Угол между двумя полюсами на проекции равен разности их широт, угол между двумя точками равен разности их долгот, когда они лежат на экваторе (горизонтальном диаметре). Для измерения угла между двумя полюсами необходимо, поворотом сетки Вульфа вокруг её центра, совместить их с экватором или меридианом, которые служат шкалой для отсчёта угловых градусов.

Стандартные проекции кристаллов Стереографическая проекция полюсов всех важнейших плоскостей и направлений кристалла с малыми индексами называется стандартной проекцией. Cтандартная проекция (стандартная сетка) кубического кристалла может рассматриваться и как стереографическая проекция (тогда в точки-полюсы проектируются кристаллографические направления), и как гномостереографическая проекция (тогда кристаллографические плоскости отображаются полюсами на сетке).

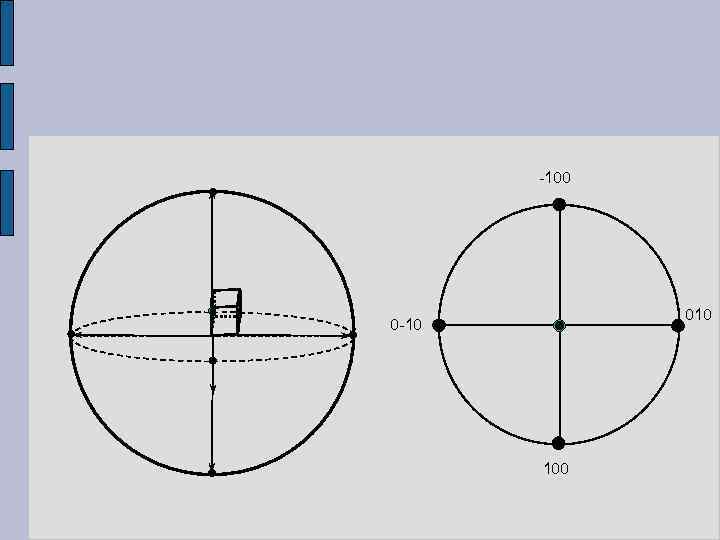
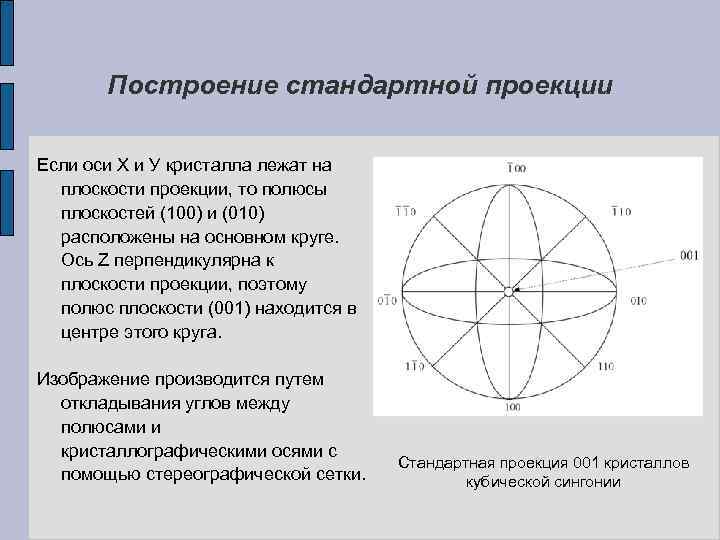Построение стандартной проекции Если оси Х и У кристалла лежат на плоскости проекции, то полюсы плоскостей (100) и (010) расположены на основном круге. Ось Z перпендикулярна к плоскости проекции, поэтому полюс плоскости (001) находится в центре этого круга. Изображение производится путем откладывания углов между полюсами и кристаллографическими осями с помощью стереографической сетки. Стандартная проекция 001 кристаллов кубической сингонии

-100 010 0 -10 100

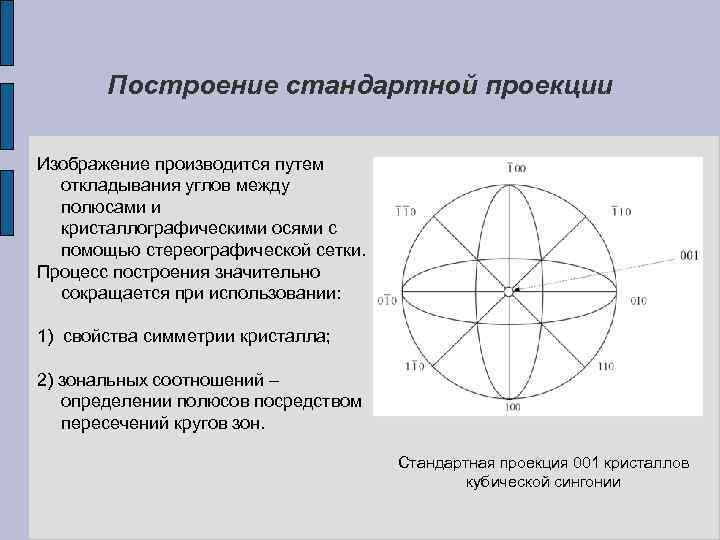Построение стандартной проекции Изображение производится путем откладывания углов между полюсами и кристаллографическими осями с помощью стереографической сетки. Процесс построения значительно сокращается при использовании: 1) свойства симметрии кристалла; 2) зональных соотношений – определении полюсов посредством пересечений кругов зон. Стандартная проекция 001 кристаллов кубической сингонии

Стандартные кристаллографические проекции для кристаллов кубической системы одинаковы для всех кристаллических веществ с кубической решёткой. Это объясняется тем, что уравнение, описывающее связь углов между плоскостями и индексами плоскостей в кубической решётке не содержит значений периодов решётки и координатных углов: Из уравнения следует, что в кубических решётках всех типов (примитивной кубической ПК, объемно-центрированной ОЦК, гранецентрированной ГЦК) с любыми периодами углы между плоскостями одинаковы кристаллографические проекции для любых веществ с кубической решёткой.

В кристаллах более низкой симметрии, чем кубическая, углы между плоскостями зависят от соотношений периодов решётки и координатных углов. Например, в тетрагональной решётке Следовательно, для кристаллов средних и низших сингоний кристаллографические проекции строятся для конкретных соотношений периодов и координатных углов. Для гексагональных кристаллов стандартные сетки (0001) построены для кристаллов с определенными соотношениями, например, с/а = 1, 86 или = 1, 633. Для кристаллов с другими с/а они не годятся. Гномостереографическая проекция для гексагональных кристаллов не совпадает с их стереографической проекцией.