Текст задача СТУД.ppt
- Количество слайдов: 23
 Текстовая задача и её решение 2 курс, 4 семестр Лыфенко Анастасия Вячеславовна к. п. н. , доцент кафедры естественноматематических дисциплин и методик их преподавания в начальных классах КГПУ им. К. Э. Циолковского 1
Текстовая задача и её решение 2 курс, 4 семестр Лыфенко Анастасия Вячеславовна к. п. н. , доцент кафедры естественноматематических дисциплин и методик их преподавания в начальных классах КГПУ им. К. Э. Циолковского 1
 Литература 1. Стойлова Л. П. Математика. – М. : Академия, 2007. , стр. 105 -139. 2. Демидова Т. Е. , Тонких А. П. Теория и практика решения текстовых задач. – М. : Академия, 2002. 3. Фридман Л. М. Как научиться решать задачи. – М. : Просвещение, 2005. , стр. 559. 2
Литература 1. Стойлова Л. П. Математика. – М. : Академия, 2007. , стр. 105 -139. 2. Демидова Т. Е. , Тонких А. П. Теория и практика решения текстовых задач. – М. : Академия, 2002. 3. Фридман Л. М. Как научиться решать задачи. – М. : Просвещение, 2005. , стр. 559. 2
 План 1. Понятие «текстовая задача» . 2. Структура текстовой задачи. 3. Классификация текстовых задач на основе соответствия числа данных и искомых. 4. Методы решения задач. 5. Способы решения задач. 6. Оформление решение задач в рамках арифметического метода. 7. Этапы работы над задачей и приемы их выполнения. 3
План 1. Понятие «текстовая задача» . 2. Структура текстовой задачи. 3. Классификация текстовых задач на основе соответствия числа данных и искомых. 4. Методы решения задач. 5. Способы решения задач. 6. Оформление решение задач в рамках арифметического метода. 7. Этапы работы над задачей и приемы их выполнения. 3
 Понятие «текстовая задача» Текстовая задача представляет собой описание на естественном языке какого-либо явления (ситуации, процесса) с требованием дать • количественную характеристику какого-либо компонента явления, • установить наличие или отсутствие некоторого отношения между компонентами, • определить вид этого отношения, • определить последовательность требуемых действий. Текстовая задача есть словесная модель ситуации, явления или процесса. 4
Понятие «текстовая задача» Текстовая задача представляет собой описание на естественном языке какого-либо явления (ситуации, процесса) с требованием дать • количественную характеристику какого-либо компонента явления, • установить наличие или отсутствие некоторого отношения между компонентами, • определить вид этого отношения, • определить последовательность требуемых действий. Текстовая задача есть словесная модель ситуации, явления или процесса. 4
 Структура текстовой задачи • Условия (данные - числовые значения величин; система функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой). • Требование или вопрос. • Решение (результат, процесс нахождения результата, действия, которые производят над данными для получения результата). 5
Структура текстовой задачи • Условия (данные - числовые значения величин; система функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой). • Требование или вопрос. • Решение (результат, процесс нахождения результата, действия, которые производят над данными для получения результата). 5
 Фломастер в 3 раза дороже карандаша, но в 2 раза дешевле книги. Сколько стоит книга, если цена карандаша 80 рублей? Условия задачи: 1. 2. 3. 4. Были куплены фломастер, карандаш, книга. Цена карандаша 80 руб. Фломастер в 3 раза дороже карандаша. Фломастер в 2 раза дешевле книги. Требование задачи: 1. Найти цену книги. 6
Фломастер в 3 раза дороже карандаша, но в 2 раза дешевле книги. Сколько стоит книга, если цена карандаша 80 рублей? Условия задачи: 1. 2. 3. 4. Были куплены фломастер, карандаш, книга. Цена карандаша 80 руб. Фломастер в 3 раза дороже карандаша. Фломастер в 2 раза дешевле книги. Требование задачи: 1. Найти цену книги. 6
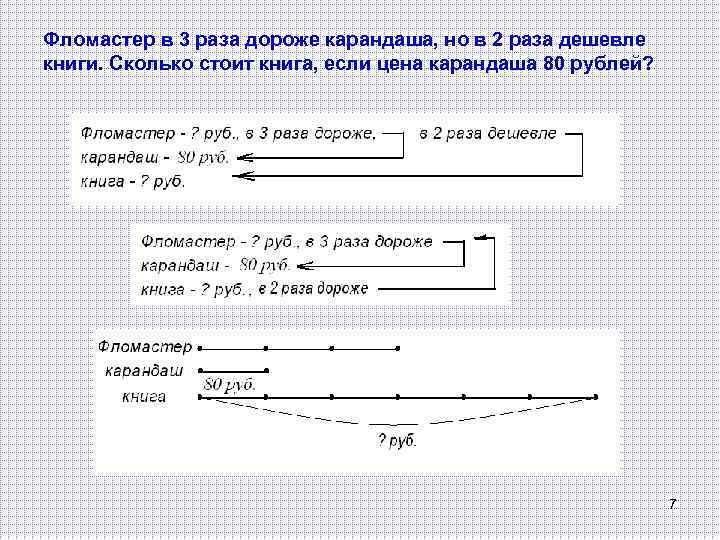 Фломастер в 3 раза дороже карандаша, но в 2 раза дешевле книги. Сколько стоит книга, если цена карандаша 80 рублей? 7
Фломастер в 3 раза дороже карандаша, но в 2 раза дешевле книги. Сколько стоит книга, если цена карандаша 80 рублей? 7
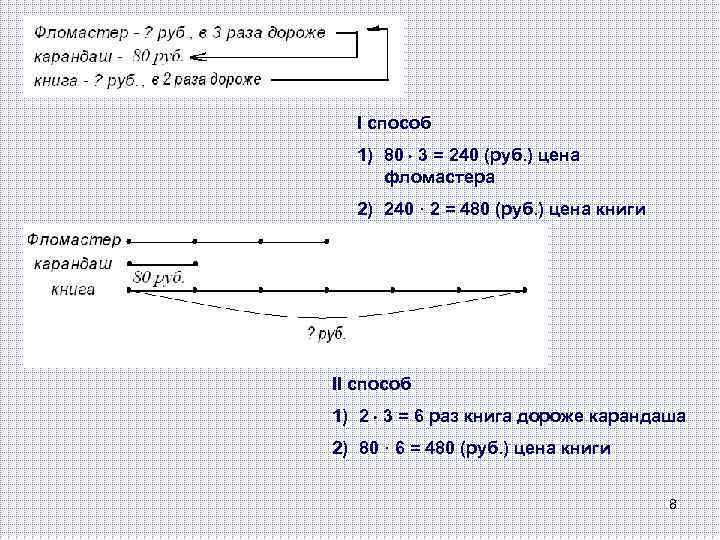 I способ 1) 80 3 = 240 (руб. ) цена фломастера 2) 240 · 2 = 480 (руб. ) цена книги II способ 1) 2 3 = 6 раз книга дороже карандаша 2) 80 · 6 = 480 (руб. ) цена книги 8
I способ 1) 80 3 = 240 (руб. ) цена фломастера 2) 240 · 2 = 480 (руб. ) цена книги II способ 1) 2 3 = 6 раз книга дороже карандаша 2) 80 · 6 = 480 (руб. ) цена книги 8
 Классификация задач на основе соответствия числа данных и искомых Определенные задачи – это задачи, в которых условий столько, сколько необходимо и достаточно для получения ответа. Задачи с альтернативным условием – это задачи, в ходе решения которых необходимо рассматривать несколько возможных вариантов условия, а ответ находится после того, как эти возможности будут исследованы. Неопределенные задачи – это задачи, в которых условий недостаточно для получения ответа. Переопределенные задачи – это задачи, имеющие условия, которые не используются при их решении выбранным способом. 9
Классификация задач на основе соответствия числа данных и искомых Определенные задачи – это задачи, в которых условий столько, сколько необходимо и достаточно для получения ответа. Задачи с альтернативным условием – это задачи, в ходе решения которых необходимо рассматривать несколько возможных вариантов условия, а ответ находится после того, как эти возможности будут исследованы. Неопределенные задачи – это задачи, в которых условий недостаточно для получения ответа. Переопределенные задачи – это задачи, имеющие условия, которые не используются при их решении выбранным способом. 9
 От одной пристани по реке одновременно отправляются два катера. Один движется со скоростью 17 км/ч, а второй – 19 км/ч. На каком расстоянии друг от друга они будут находится через 2 часа, если скорость течения реки 2 км/ч? Сумма трех чисел равна 100. Сумма двух из них равна 80, а первое число на 20 больше второго. Найдите эти числа. Из пункта А в пункт В вышел поезд со скоростью 60 км/ч. Спустя 3 часа из пункта В навстречу ему вышел другой поезд, скорость которого на 10 км/ч больше, чем у первого. Расстояние между пунктами 570 км. Сколько часов до встречи был в пути второй поезд, если его скорость в 1, 5 раза больше скорости первого поезда? 10
От одной пристани по реке одновременно отправляются два катера. Один движется со скоростью 17 км/ч, а второй – 19 км/ч. На каком расстоянии друг от друга они будут находится через 2 часа, если скорость течения реки 2 км/ч? Сумма трех чисел равна 100. Сумма двух из них равна 80, а первое число на 20 больше второго. Найдите эти числа. Из пункта А в пункт В вышел поезд со скоростью 60 км/ч. Спустя 3 часа из пункта В навстречу ему вышел другой поезд, скорость которого на 10 км/ч больше, чем у первого. Расстояние между пунктами 570 км. Сколько часов до встречи был в пути второй поезд, если его скорость в 1, 5 раза больше скорости первого поезда? 10
 Методы решения задач Арифметический метод предполагает решение задачи посредством выполнения арифметических действий над числами. Алгебраический метод предполагает решение задачи с помощью уравнения, неравенства или их систем. Практический метод предполагает решение посредством выполнения практических действий. 11
Методы решения задач Арифметический метод предполагает решение задачи посредством выполнения арифметических действий над числами. Алгебраический метод предполагает решение задачи с помощью уравнения, неравенства или их систем. Практический метод предполагает решение посредством выполнения практических действий. 11
 У Лены было 12 конфет, из них 4 были ириски, 3 – шоколадные, а остальные карамель. Сколько карамелей было у Лены? 1) 4+3=7 (к. ) ириски и шоколадные конфеты. 2) 12 -7=5 (к. ) карамелей. Пусть х – это количество карамелей. Тогда всех конфет 4+3+х или 12. Составим уравнение: 4+3+х=12. Решим уравнение. 12
У Лены было 12 конфет, из них 4 были ириски, 3 – шоколадные, а остальные карамель. Сколько карамелей было у Лены? 1) 4+3=7 (к. ) ириски и шоколадные конфеты. 2) 12 -7=5 (к. ) карамелей. Пусть х – это количество карамелей. Тогда всех конфет 4+3+х или 12. Составим уравнение: 4+3+х=12. Решим уравнение. 12
 Способы решения задач отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи. 1) 12 – 4 = 8 (к. ) шоколадных и карамелей. 2) 8 – 3 = 5 (к. ) карамелей. 1) 12 – 3 = 9 (к. ) 2) 9 – 4 = 5 (к. ) 4 + х = 12 – 3 х + 3 = 12 - 4 13
Способы решения задач отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи. 1) 12 – 4 = 8 (к. ) шоколадных и карамелей. 2) 8 – 3 = 5 (к. ) карамелей. 1) 12 – 3 = 9 (к. ) 2) 9 – 4 = 5 (к. ) 4 + х = 12 – 3 х + 3 = 12 - 4 13
 Оформление решение задач По действиям с вопросами 1) Сколько ирисок и шоколадных конфет было у Лены? 4+3=7 (к. ) 2) Сколько карамелей было у Лены? 12 -7=5 (к. ) карамелей. Ответ: 5 карамелей было у Лены. По действиям с пояснениями По действиям без пояснений Выражением 12 – (4 + 3) = 5 14
Оформление решение задач По действиям с вопросами 1) Сколько ирисок и шоколадных конфет было у Лены? 4+3=7 (к. ) 2) Сколько карамелей было у Лены? 12 -7=5 (к. ) карамелей. Ответ: 5 карамелей было у Лены. По действиям с пояснениями По действиям без пояснений Выражением 12 – (4 + 3) = 5 14
 Этапы работы над задачей и приемы их выполнения 1. Анализ задачи предполагает выделение всех данных, неизвестных, искомых, отношений между ними, то есть сводится к пониманию ситуации, описанной в задаче. Приемы выполнения: • задать специальные вопросы; • переформулировать текст задачи; • построение вспомогательной модели; 15
Этапы работы над задачей и приемы их выполнения 1. Анализ задачи предполагает выделение всех данных, неизвестных, искомых, отношений между ними, то есть сводится к пониманию ситуации, описанной в задаче. Приемы выполнения: • задать специальные вопросы; • переформулировать текст задачи; • построение вспомогательной модели; 15
 За 35 тетрадей уплатили 420 рублей. Сколько нужно уплатить за 16 блокнотов, если блокнот на 3 рубля дешевле тетради? Стоимость 35 тетрадей - 420 рублей. Какова стоимость 16 блокнотов, если цена блокнота на 3 рубля меньше цены тетради? Цена Количество Стоимость Т. ? руб. 35 шт. 420 руб. Б. ? руб. , на 3 рубля дешевле 16 шт. ? руб. 16
За 35 тетрадей уплатили 420 рублей. Сколько нужно уплатить за 16 блокнотов, если блокнот на 3 рубля дешевле тетради? Стоимость 35 тетрадей - 420 рублей. Какова стоимость 16 блокнотов, если цена блокнота на 3 рубля меньше цены тетради? Цена Количество Стоимость Т. ? руб. 35 шт. 420 руб. Б. ? руб. , на 3 рубля дешевле 16 шт. ? руб. 16
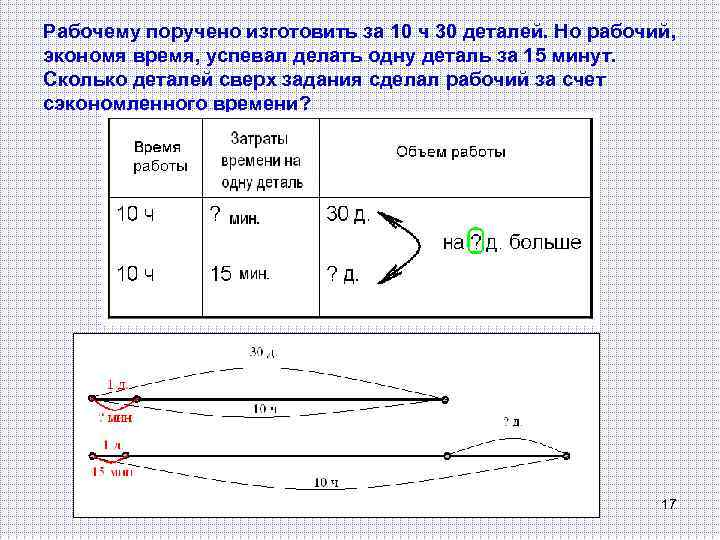 Рабочему поручено изготовить за 10 ч 30 деталей. Но рабочий, экономя время, успевал делать одну деталь за 15 минут. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени? 17
Рабочему поручено изготовить за 10 ч 30 деталей. Но рабочий, экономя время, успевал делать одну деталь за 15 минут. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени? 17
 2. Поиск и составление плана решения предполагает установление связи между данными, определение последовательности действий. Приемы выполнения: • разбор задачи по тексту или вспомогательной модели от вопроса к данным; • разбор задачи по тексту или вспомогательной модели от данных к вопросу. 18
2. Поиск и составление плана решения предполагает установление связи между данными, определение последовательности действий. Приемы выполнения: • разбор задачи по тексту или вспомогательной модели от вопроса к данным; • разбор задачи по тексту или вспомогательной модели от данных к вопросу. 18
 3. Осуществление плана решения предполагает выполнение действий, приводящих к ответу. Приемы выполнения: • запись решения по действиям; • запись решения выражением. 19
3. Осуществление плана решения предполагает выполнение действий, приводящих к ответу. Приемы выполнения: • запись решения по действиям; • запись решения выражением. 19
 4. Проверка решения предполагает установление правильности или ошибочности проведенного решения. Приемы выполнения: • установление соответствия между условием и результатом; • решение задачи другим способом или методом. 20
4. Проверка решения предполагает установление правильности или ошибочности проведенного решения. Приемы выполнения: • установление соответствия между условием и результатом; • решение задачи другим способом или методом. 20
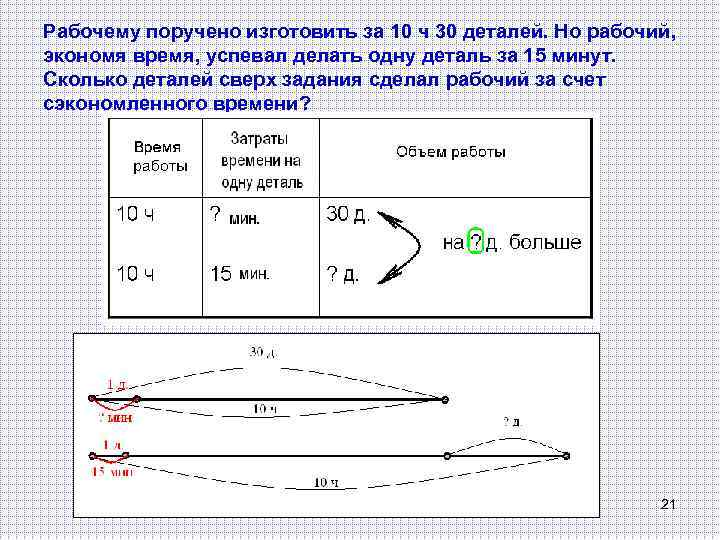 Рабочему поручено изготовить за 10 ч 30 деталей. Но рабочий, экономя время, успевал делать одну деталь за 15 минут. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени? 21
Рабочему поручено изготовить за 10 ч 30 деталей. Но рабочий, экономя время, успевал делать одну деталь за 15 минут. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени? 21
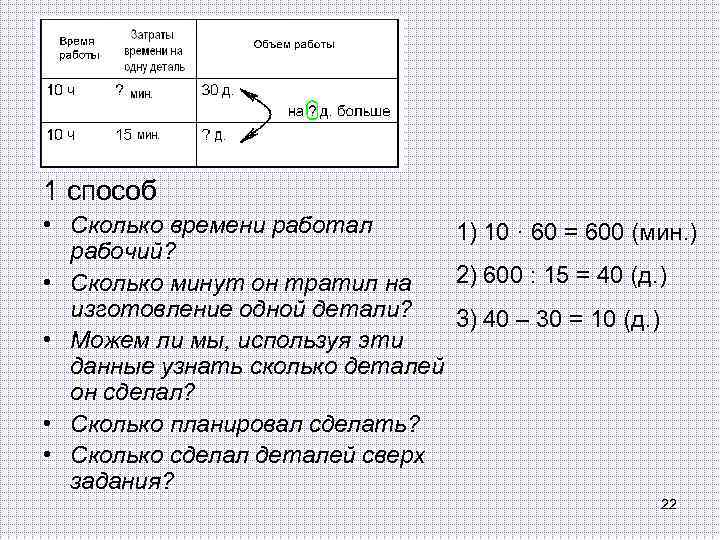 1 способ • Сколько времени работал 1) 10 · 60 = 600 (мин. ) рабочий? 2) 600 : 15 = 40 (д. ) • Сколько минут он тратил на изготовление одной детали? 3) 40 – 30 = 10 (д. ) • Можем ли мы, используя эти данные узнать сколько деталей он сделал? • Сколько планировал сделать? • Сколько сделал деталей сверх задания? 22
1 способ • Сколько времени работал 1) 10 · 60 = 600 (мин. ) рабочий? 2) 600 : 15 = 40 (д. ) • Сколько минут он тратил на изготовление одной детали? 3) 40 – 30 = 10 (д. ) • Можем ли мы, используя эти данные узнать сколько деталей он сделал? • Сколько планировал сделать? • Сколько сделал деталей сверх задания? 22
 Рабочему поручено изготовить за 10 ч 30 деталей. Но рабочий, экономя время, успевал делать одну деталь за 15 минут. Сколько деталей сверх задания сделала рабочий за счет сэкономленного времени? 2 способ 3 способ 4 способ 1) 60 · 10 = 600 (мин) 1) 60 : 15 = 4 (д. ) 2) 600 : 30 = 20 (мин) 2) 15 · 30 = 450 (мин) 2) 4 · 10 = 40 (д. ) 3) 20 – 15 = 5 (мин) 3) 600 – 450 = 150 (мин) 3) 40 – 30 = 10 (д. ) 4) 5 · 30 = 150 (мин) 4) 150 : 15 = 10 (д. ) 5) 150 : 15 = 10 (д. ) • • • выделение величин и отношений между ними (таблица); беседа; обоснование решения; продолжение решения; выбор рационального решения. 23
Рабочему поручено изготовить за 10 ч 30 деталей. Но рабочий, экономя время, успевал делать одну деталь за 15 минут. Сколько деталей сверх задания сделала рабочий за счет сэкономленного времени? 2 способ 3 способ 4 способ 1) 60 · 10 = 600 (мин) 1) 60 : 15 = 4 (д. ) 2) 600 : 30 = 20 (мин) 2) 15 · 30 = 450 (мин) 2) 4 · 10 = 40 (д. ) 3) 20 – 15 = 5 (мин) 3) 600 – 450 = 150 (мин) 3) 40 – 30 = 10 (д. ) 4) 5 · 30 = 150 (мин) 4) 150 : 15 = 10 (д. ) 5) 150 : 15 = 10 (д. ) • • • выделение величин и отношений между ними (таблица); беседа; обоснование решения; продолжение решения; выбор рационального решения. 23


