Tehneline joonestamine Tallinna Lasnamae Mehaanikakool 1 JOONTELIIGID

Tehneline joonestamine Tallinna Lasnamae Mehaanikakool 1

JOONTELIIGID JA KASUTUSALAD Vastab ISO 128 -24: 1999 Nimetus 1. Pidev jämejoon e põhijoon 2. Pidev peenjoon Joone näidis Jämedus põhijoone s suhtes s=0, 13. . 2 mm Eelistatavd s=0, 25 ja 0, 5 s=0, 35, 0, 7 ja 0, 9 s/2 Kasutusalad Nähtavad kontuurjooned. Nähtavad üleminekujooned. Ristlõike kontuurid (nii väljatoodud kui ka lõike koosseisu kuuluval ristlõikel). Lõigete ja ristlõigete noolte jooned. Distants- ja mõõtejooned. Viirutusjooned. Viitejooned nende riiulid ja pealkirjade jooned. Paindejooned pinnalaotustel ja tasapinnalistel detailidel. Projektsioonpindade ühisjooned e teljed, tasapindade jäljed, iseloomulike punktide konstruktsioonijooned. 2

JOONTELIIGID JA KASUTUSALAD Vastab ISO 128 -24: 1999 Nimetus 3. Kriipsjoon Joone näidis Jämedus põhijoone s suhtes s/2 Kasutusalad Varjatud kontuurjooned ja üleminekujooned. 4. Kriipspunktpeenjoon s/2 Telg- ja tsentrijooned. Vaate peale joonestatud ja väljatoodud ristlõigete sümmeetriateljed. 5. Pidev vabakäejoon s/2 Katkestusjooned. 3

NORMKIRI B-tüüpi kaldkiri. Ladina tähestik, märgid ja numbrid 4

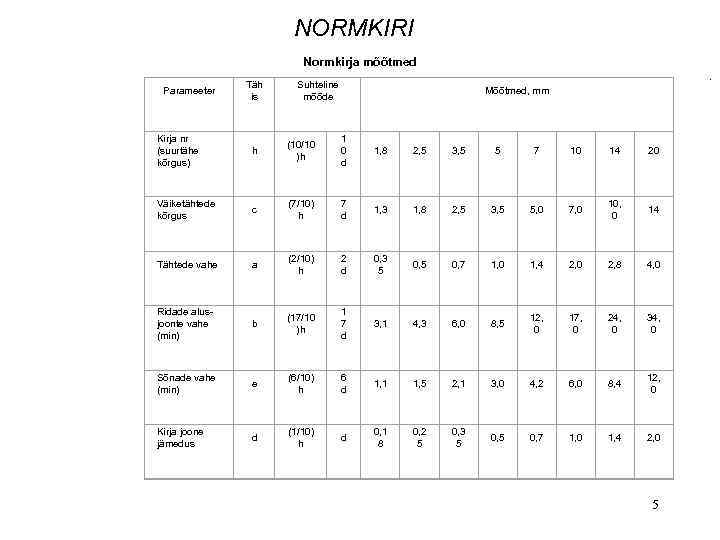NORMKIRI Normkirja mõõtmed Parameeter Täh is . Suhteline mõõde Mõõtmed, mm Kirja nr (suurtähe kõrgus) h (10/10 )h 1 0 d 1, 8 2, 5 3, 5 5 7 10 14 20 Väiketähtede kõrgus c (7/10) h 7 d 1, 3 1, 8 2, 5 3, 5 5, 0 7, 0 10, 0 14 Tähtede vahe a (2/10) h 2 d 0, 3 5 0, 7 1, 0 1, 4 2, 0 2, 8 4, 0 Ridade alusjoonte vahe (min) b (17/10 )h 1 7 d 3, 1 4, 3 6, 0 8, 5 12, 0 17, 0 24, 0 34, 0 Sõnade vahe (min) e (6/10) h 6 d 1, 1 1, 5 2, 1 3, 0 4, 2 6, 0 8, 4 12, 0 Kirja joone jämedus d (1/10) h d 0, 1 8 0, 2 5 0, 3 5 0, 7 1, 0 1, 4 2, 0 5

FORMAADID ISO 5457: 1999 JÄRGI • • • A 0 mõõtmetega 841 x 1189 A 1 mõõtmetega 594 x 841 A 2 mõõtmetega 420 x 594 A 3 297 x 420 A 4 297 x 210 6

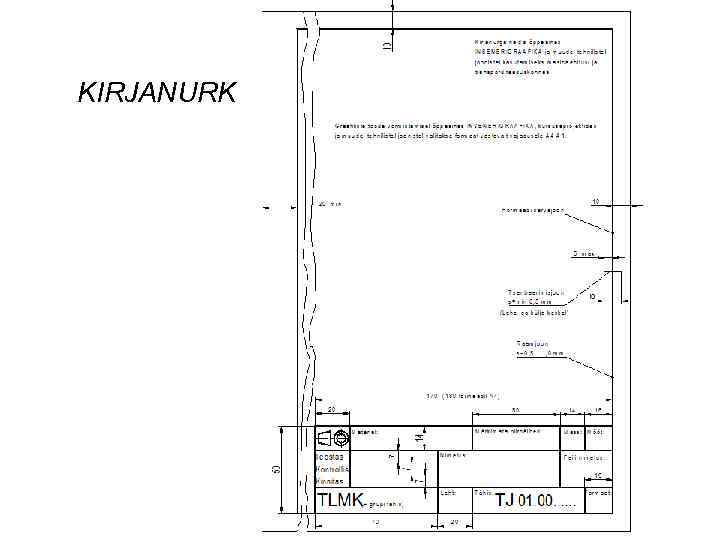KIRJANURK 7

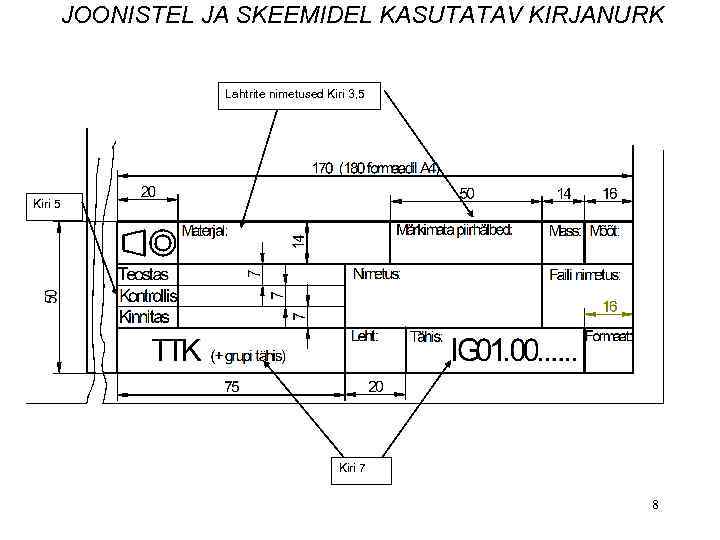JOONISTEL JA SKEEMIDEL KASUTATAV KIRJANURK Lahtrite nimetused Kiri 3, 5 Kiri 7 8

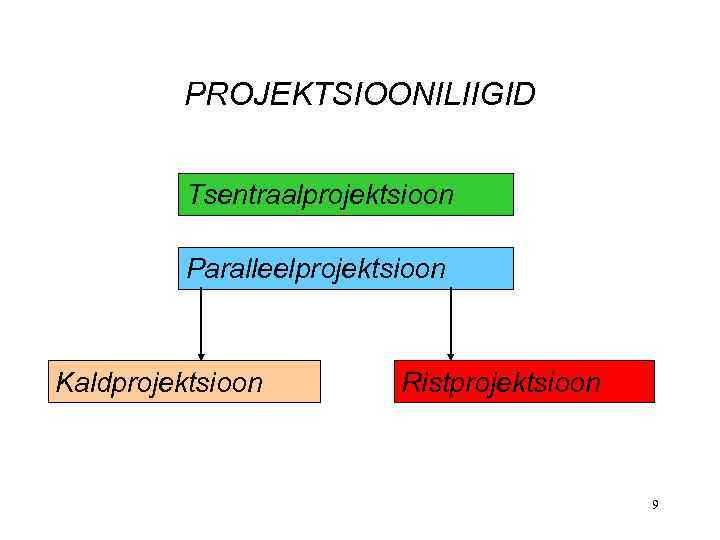PROJEKTSIOONILIIGID Tsentraalprojektsioon Paralleelprojektsioon Kaldprojektsioon Ristprojektsioon 9

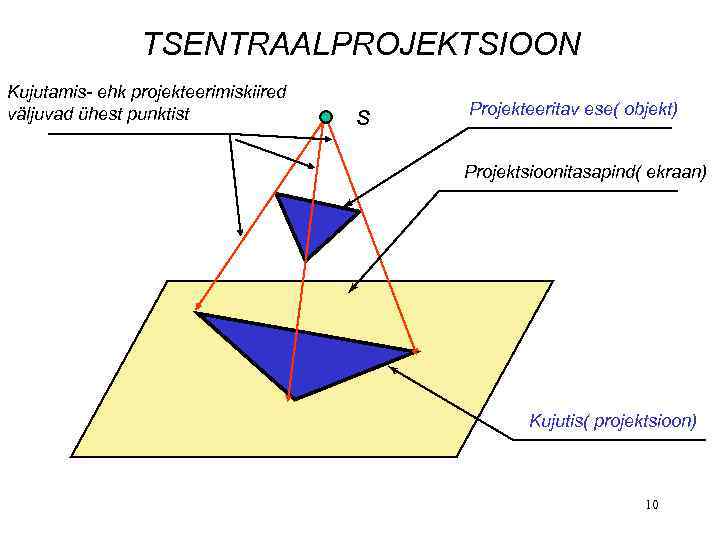TSENTRAALPROJEKTSIOON Kujutamis- ehk projekteerimiskiired väljuvad ühest punktist s Projekteeritav ese( objekt) Projektsioonitasapind( ekraan) Kujutis( projektsioon) 10

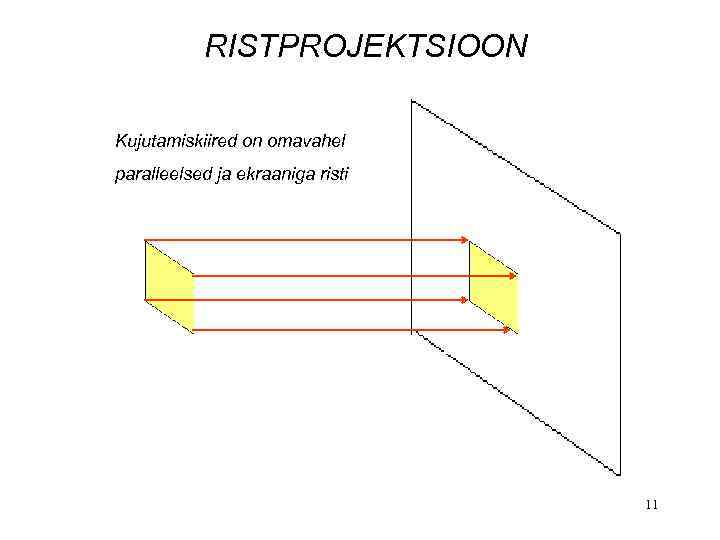RISTPROJEKTSIOON Kujutamiskiired on omavahel paralleelsed ja ekraaniga risti 11

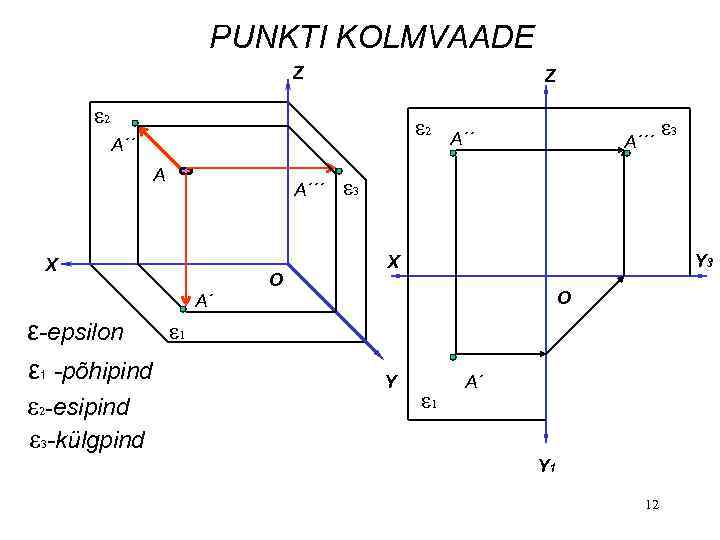PUNKTI KOLMVAADE Z Z ε 2 A´´ A A´´´ X O A´´´ ε 3 Y 3 X O A´ ε 1 ε-epsilon ε 1 -põhipind ε 2 -esipind ε 3 -külgpind ε 3 Y ε 1 A´ Y 1 12

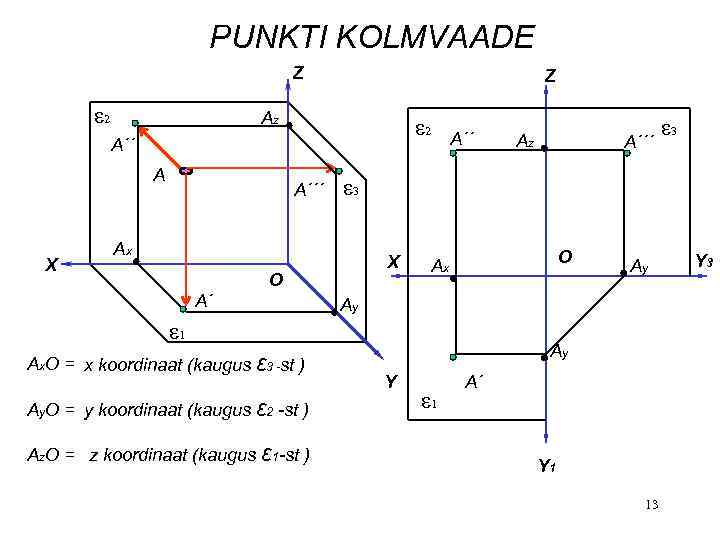PUNKTI KOLMVAADE Z ε 2 Z Az ε 2 A´´ A X A´´´ X O Ay. O = y koordinaat (kaugus ε 2 -st ) Az. O = z koordinaat (kaugus ε 1 -st ) A´´´ O Ax Ay Ay ε 1 Ax. O = x koordinaat (kaugus ε 3 -st ) Az ε 3 Ax A´ A´´ Ay Y ε 1 A´ Y 1 13 Y 3

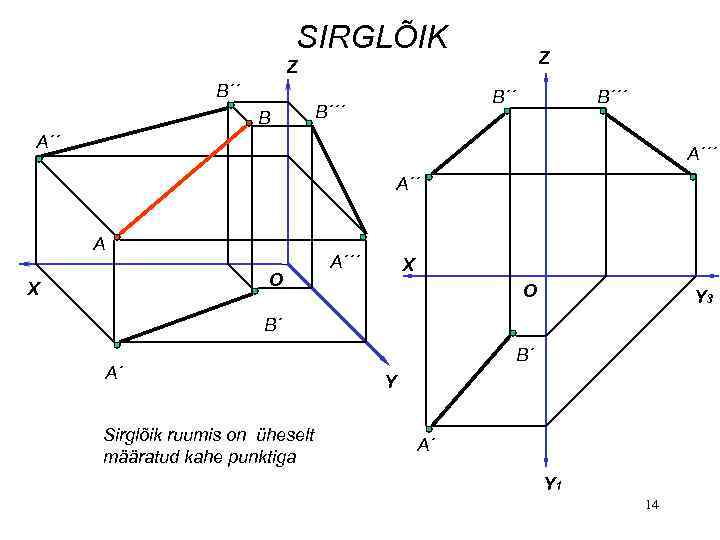SIRGLÕIK Z Z B´´ B´´´ A´´ A O X A´´´ X O Y 3 B´ A´ Sirglõik ruumis on üheselt määratud kahe punktiga B´ Y A´ Y 1 14

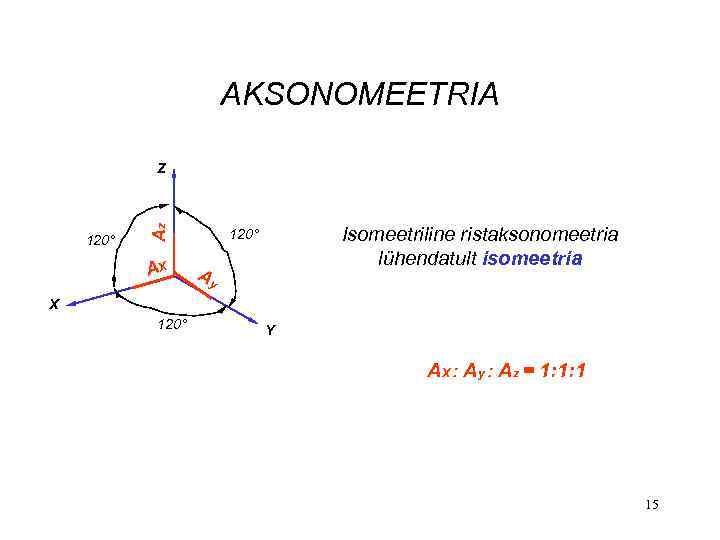AKSONOMEETRIA 120° Az Z AX Isomeetriline ristaksonomeetria lühendatult isomeetria 120° Ay X 120° Y AX : Ay : Az = 1: 1: 1 15

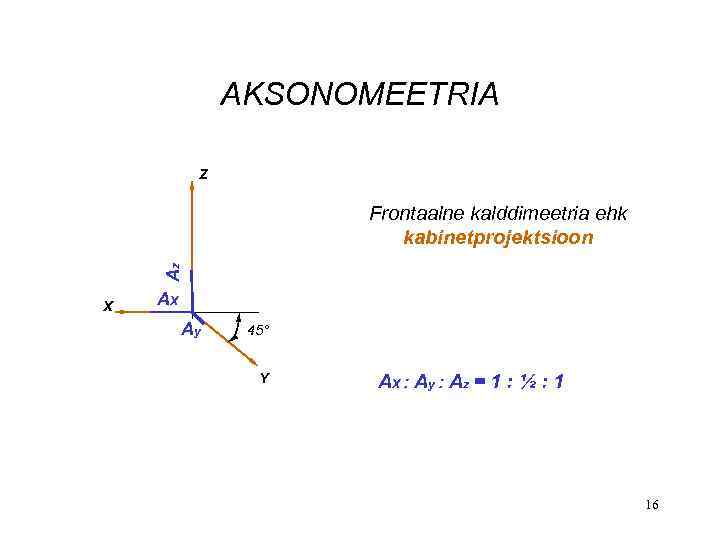AKSONOMEETRIA Z Az Frontaalne kalddimeetria ehk kabinetprojektsioon X AX Ay 45° Y AX : Ay : Az = 1 : ½ : 1 16

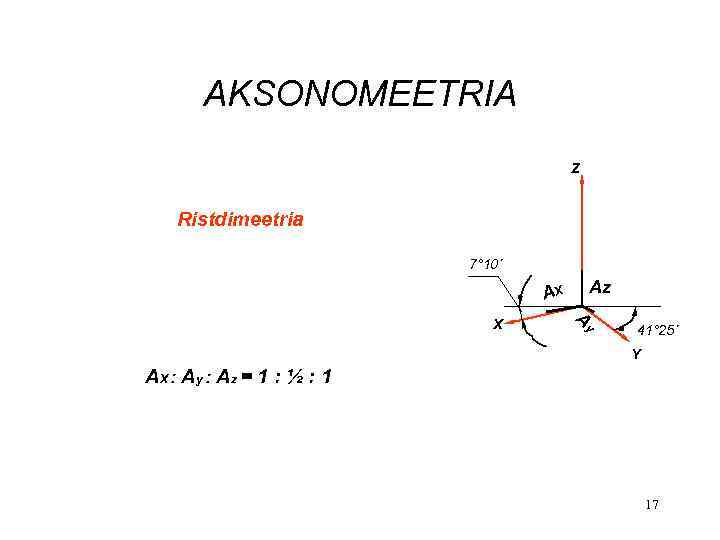AKSONOMEETRIA Z Ristdimeetria 7° 10´ AX X Az Ay 41° 25´ Y AX : Ay : Az = 1 : ½ : 1 17

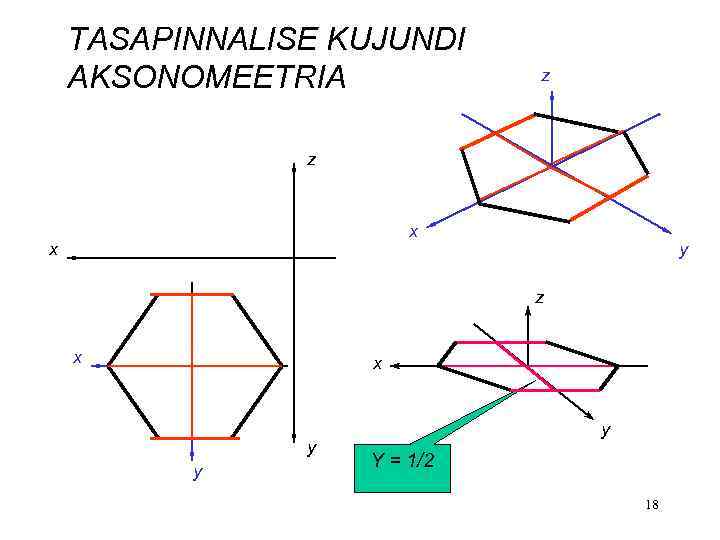TASAPINNALISE KUJUNDI AKSONOMEETRIA z z x x y y y Y = 1/2 18

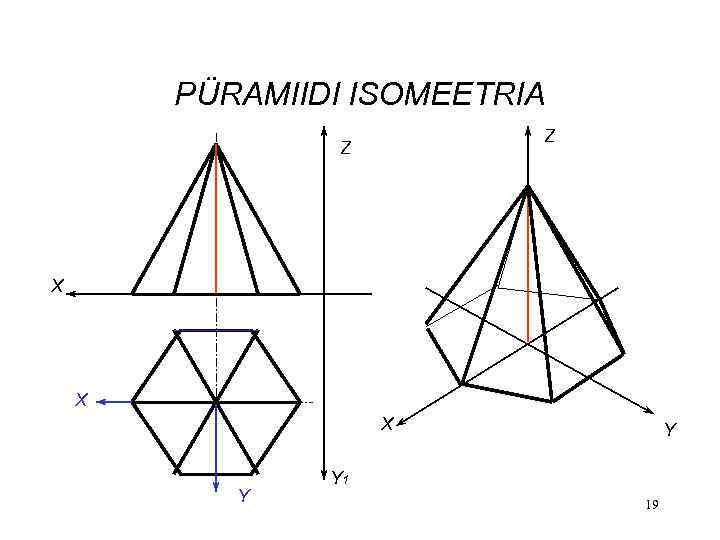PÜRAMIIDI ISOMEETRIA Z Z X X X Y Y Y 1 19

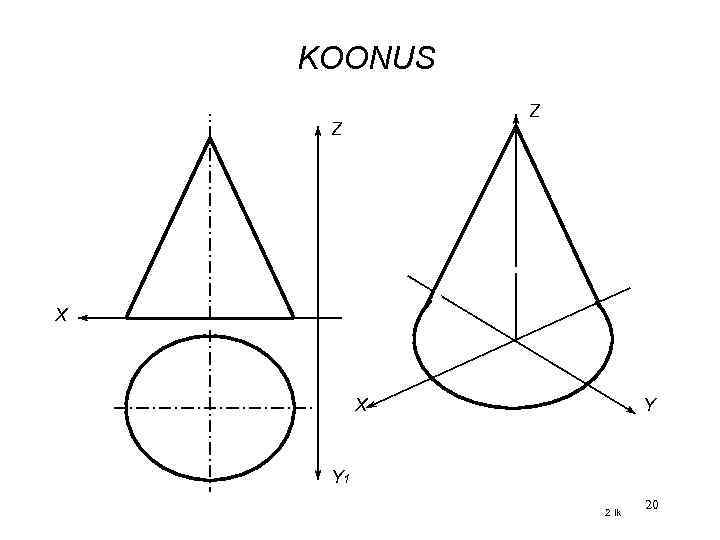KOONUS Z Z X X Y Y 1 2 lk 20

PUNKT JA SIRGE Punkt asub sirgel kui tema projektsioonid asuvad selle sirge vastavatel projektsioonidel 21

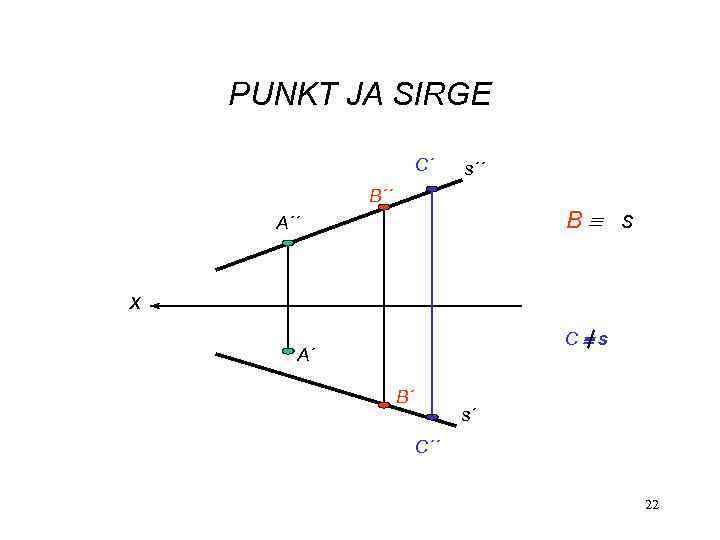PUNKT JA SIRGE C´ s´´ B s A´´ x C s A´ B´ s´ C´´ 22

SIRGE ASEND RUUMIS Asendi järgi projektsioonipindade suhtes jagunevad sirged: • Üldasendilised • Eriasendilised Üldasendiline sirge ei ole paralleelne ega risti ühegi projektsioonitasapinnaga Eriasendiline sirge on paralleelne või risti mistahes projektsionitasapinnaga 23

ERIASENDILISED SIRGED • NIVOOSIRGE(horisontaal, frontaal) – on sirge, mis on paralleelne mistahes projektsioonitasapinnaga • PROJEKTEERIV SIRGE – on sirge, mis on risti mistahes projektsioonitasapinnaga 24

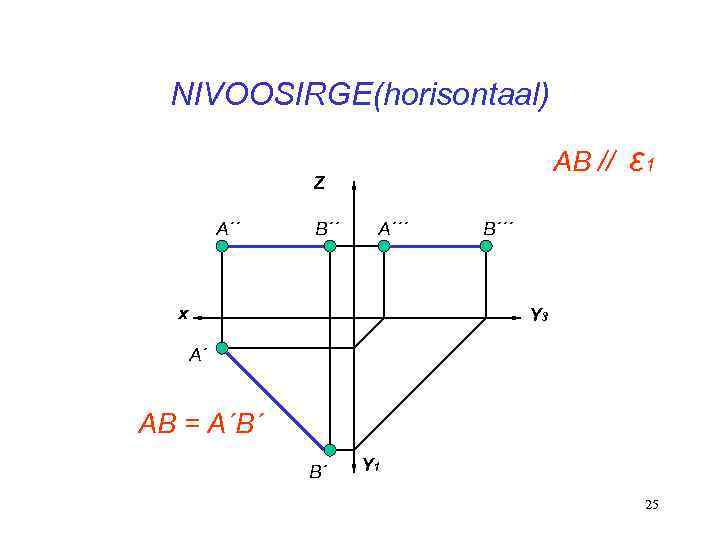NIVOOSIRGE(horisontaal) AB // Z A´´ B´´ A´´´ x ε 1 B´´´ Y 3 A´ AB = A´B´ B´ Y 1 25

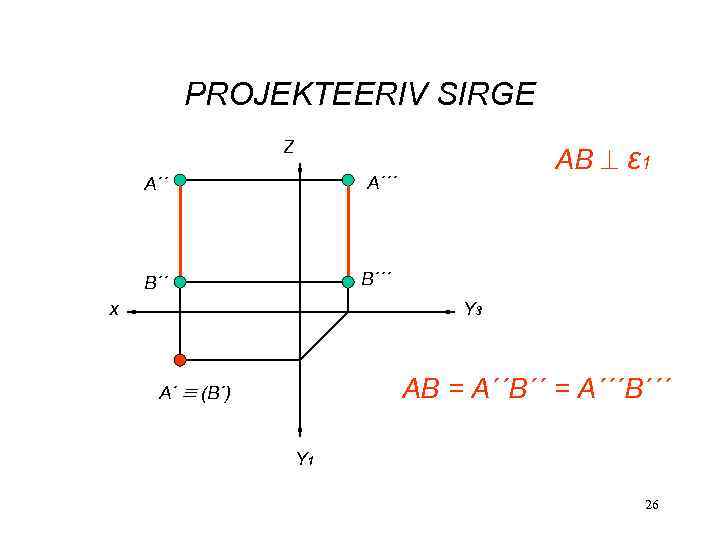PROJEKTEERIV SIRGE Z AB ε 1 A´´´ A´´ B´´ x Y 3 AB = A´´B´´ = A´´´B´´´ A´ (B´) Y 1 26

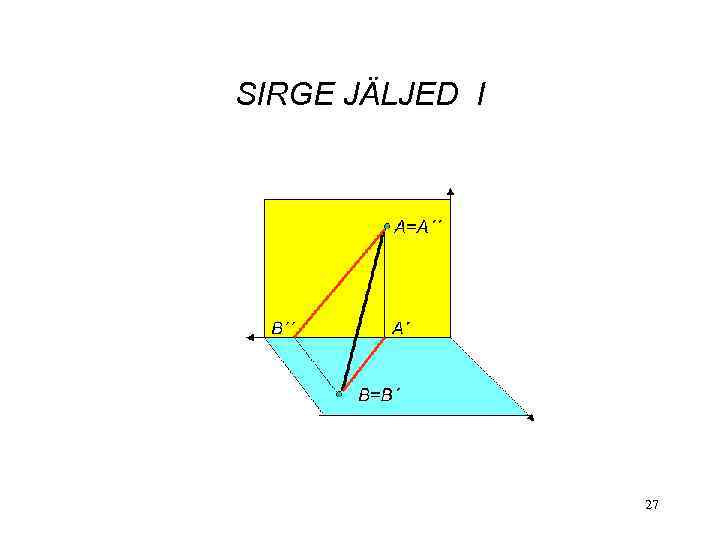SIRGE JÄLJED I 27

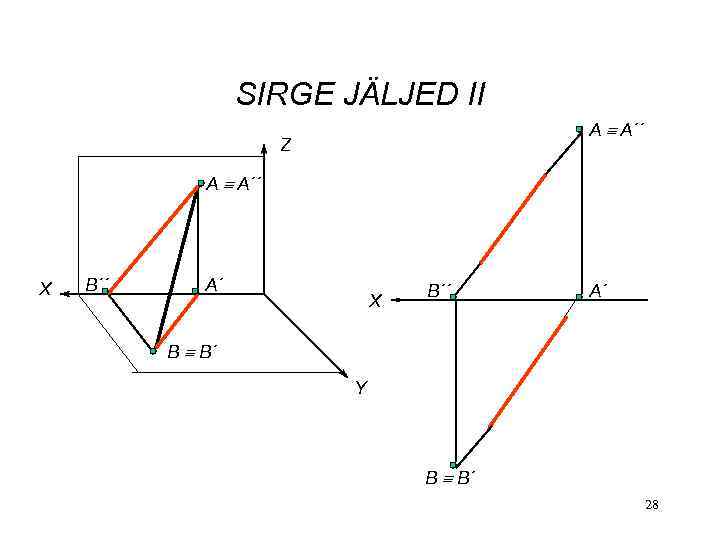SIRGE JÄLJED II A A´´ Z A A´´ X B´´ A´ B B´ Y B B´ 28

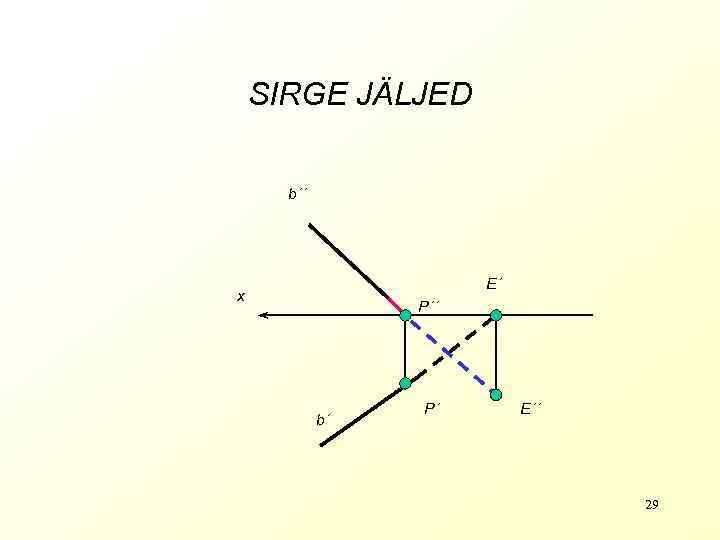SIRGE JÄLJED b´´ E´ x P´´ b´ P´ E´´ 29

SIRGETE VASTASTIKUSED ASENDID • Paralleelsed sirged • Lõikuvad sirged • Kiivsirged 30

PARALLEELSED SIRGED • Sirged on paralleelsed kui nende samanimelised projektsioonid on paralleelsed s // u, sest s´ // u´ ja s´´ // u´´ 31

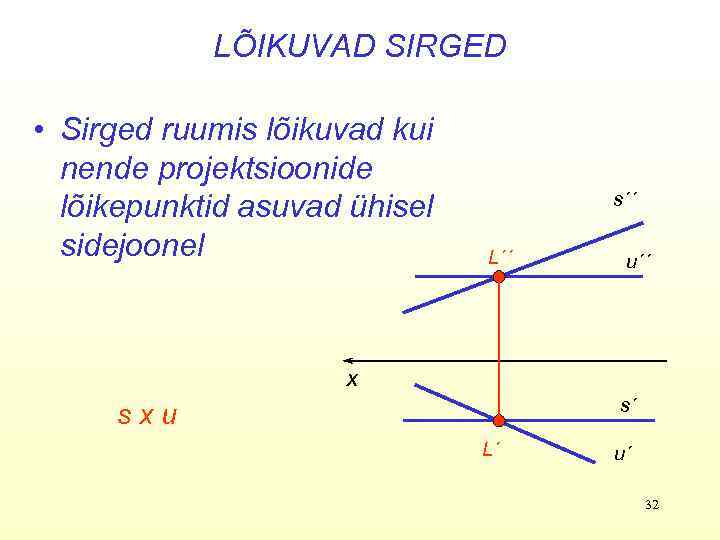LÕIKUVAD SIRGED • Sirged ruumis lõikuvad kui nende projektsioonide lõikepunktid asuvad ühisel sidejoonel s´´ L´´ u´´ x s´ sxu L´ u´ 32

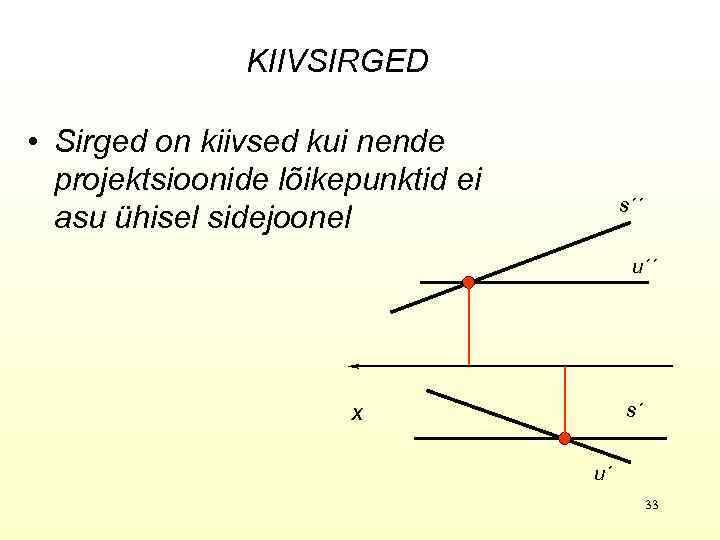KIIVSIRGED • Sirged on kiivsed kui nende projektsioonide lõikepunktid ei asu ühisel sidejoonel s´´ u´´ x s´ u´ 33

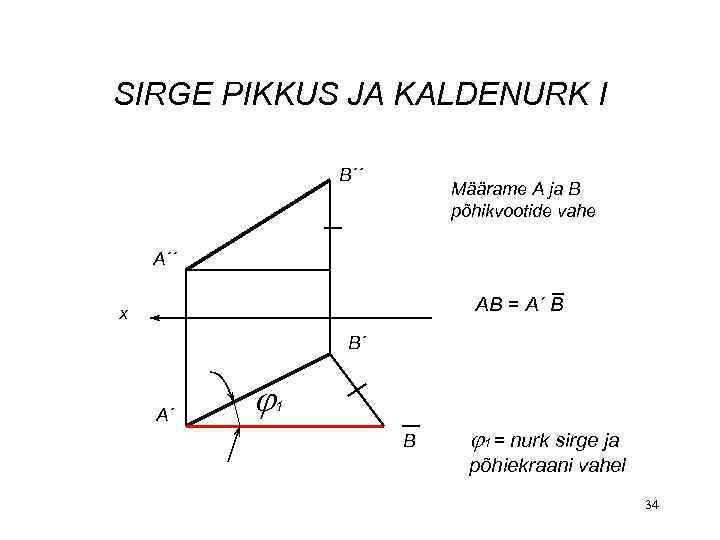SIRGE PIKKUS JA KALDENURK I B´´ Määrame A ja B põhikvootide vahe A´´ AB = A´ B x B´ A´ 1 B 1 = nurk sirge ja põhiekraani vahel 34

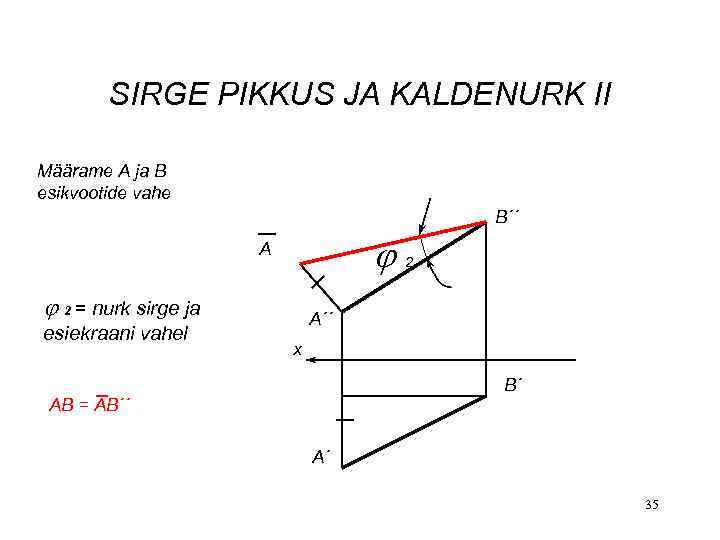SIRGE PIKKUS JA KALDENURK II Määrame A ja B esikvootide vahe B´´ A 2 = nurk sirge ja esiekraani vahel 2 A´´ x B´ AB = AB´´ A´ 35

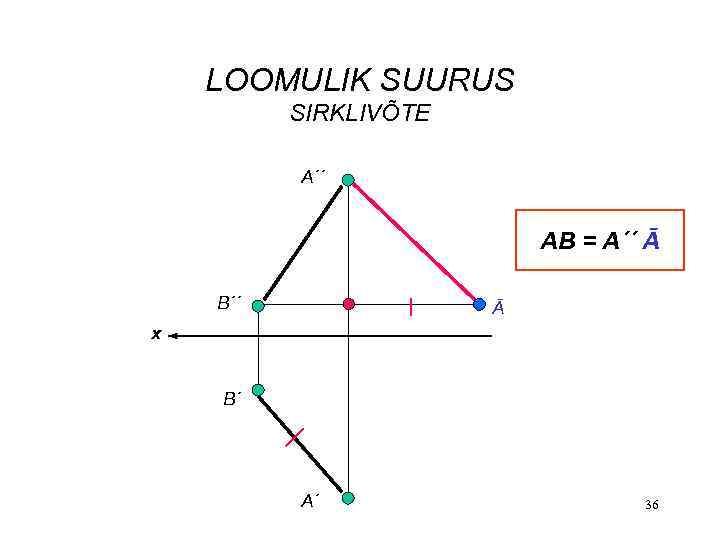LOOMULIK SUURUS SIRKLIVÕTE A´´ AB = A´´ Ā B´´ Ā x B´ A´ 36

TASAPINNA MÄÄRAMISANDMED I TASAPIND ON RUUMIS ÜHESELT MÄÄRATUD 1. 2. 3. 4. Kolme mitte ühel sirgel asuva punktiga Sirge ja punktiga väljaspool sirget Kahe lõikuva sirgega Kahe paralleelse sirgega 37

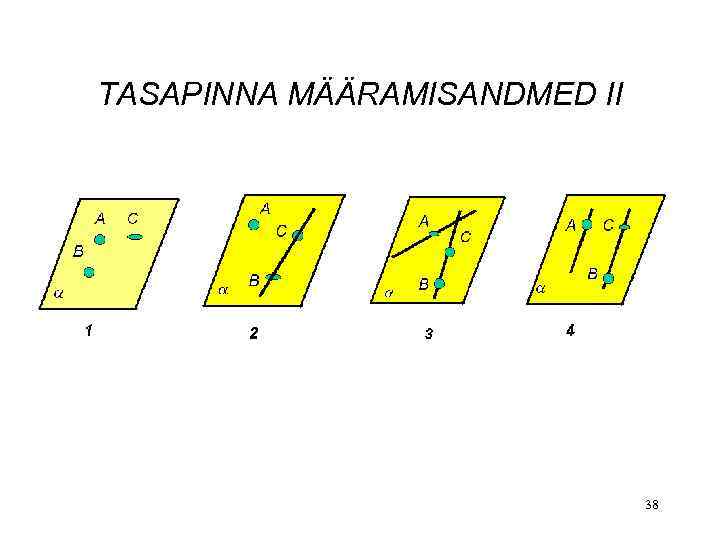TASAPINNA MÄÄRAMISANDMED II 38

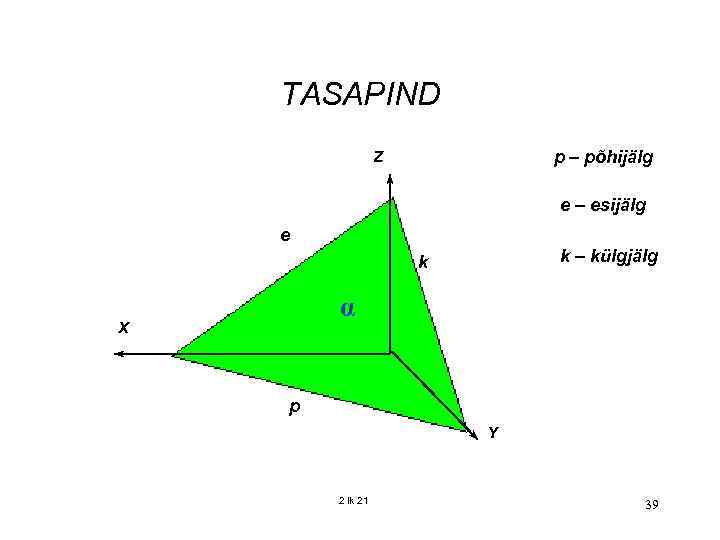TASAPIND p – põhijälg Z e – esijälg e k – külgjälg k α X p Y 2 lk 21 39

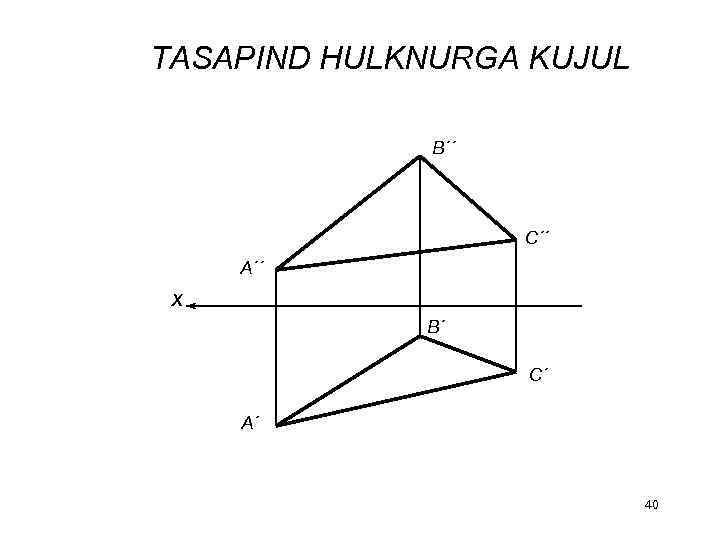TASAPIND HULKNURGA KUJUL B´´ C´´ A´´ x B´ C´ A´ 40

TASAPINNA ASEND RUUMIS Asendi järgi projektsioonitasapindade suhtes jagunevad tasapinnad: • Üldasendilised • Eriasendilised Üldasendiline tasapind ei ole paralleelne ega risti ühegi projektsioonitasapinnaga Eriasendiline tasapind on risti või paralleelne mistahes projektsionitasapinnaga 41

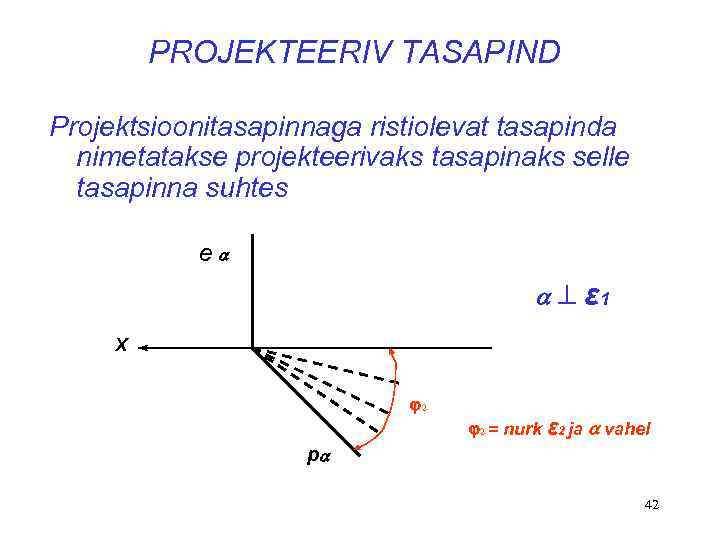PROJEKTEERIV TASAPIND Projektsioonitasapinnaga ristiolevat tasapinda nimetatakse projekteerivaks tasapinaks selle tasapinna suhtes e ε 1 X 2 2 = nurk ε 2 ja vahel p 42

NIVOOTASAPIND Projektsioonipinnaga paralleelset tasapinda nimetatakse nivootasapinnaks selle projektsioonitasapinna suhtes Z // ε 1 k e X Y 3 ε 2 ja ε 3 Y 1 43

TASAPINNA NIVOOJOONED • Tasapinna nivoojoonteks on horisontaal (h) ja frontaal (f) • Horisontaal on tasapinnal asetsev joon, mis on // põhiekraaniga (ε 1) • Frontaal on tasapinnal asetsev joon, mis on // esiekraaniga (ε 2) 44

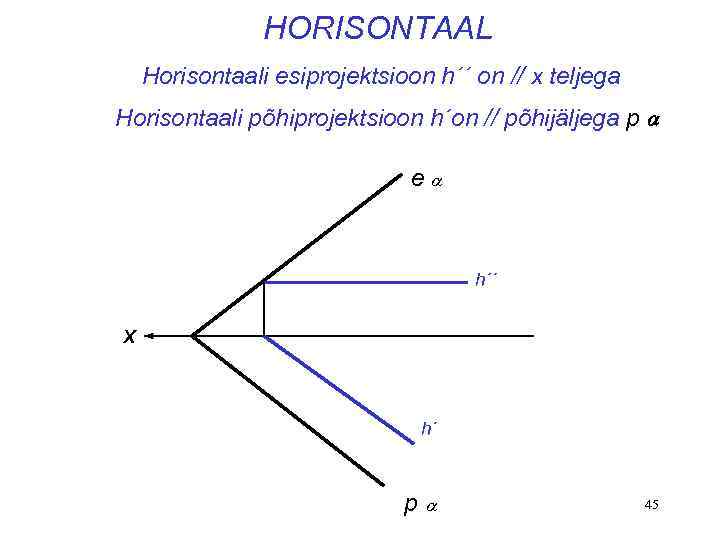HORISONTAAL Horisontaali esiprojektsioon h´´ on // x teljega Horisontaali põhiprojektsioon h´on // põhijäljega p e h´´ X h´ p 45

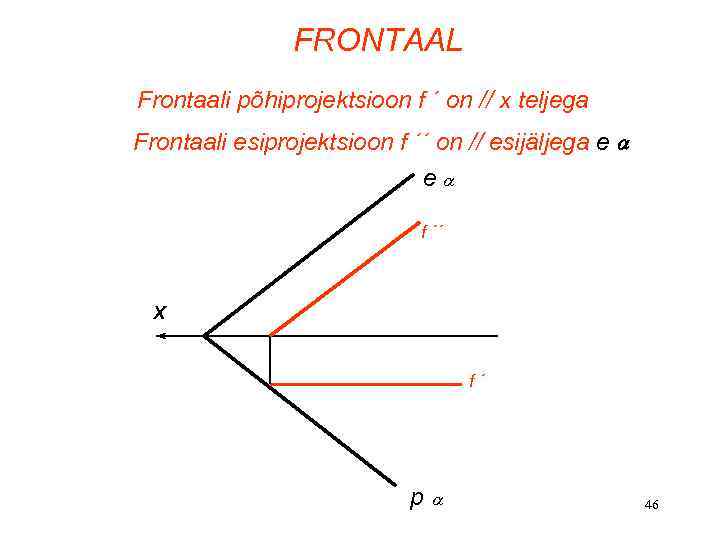FRONTAAL Frontaali põhiprojektsioon f ´ on // x teljega Frontaali esiprojektsioon f ´´ on // esijäljega e e f ´´ X f´ p 46

PUNKT TASAPINNAL Punkt asetseb tasapinnal kui temast saab läbi panna sirge, mis asetseb sellel tasapinnal 47

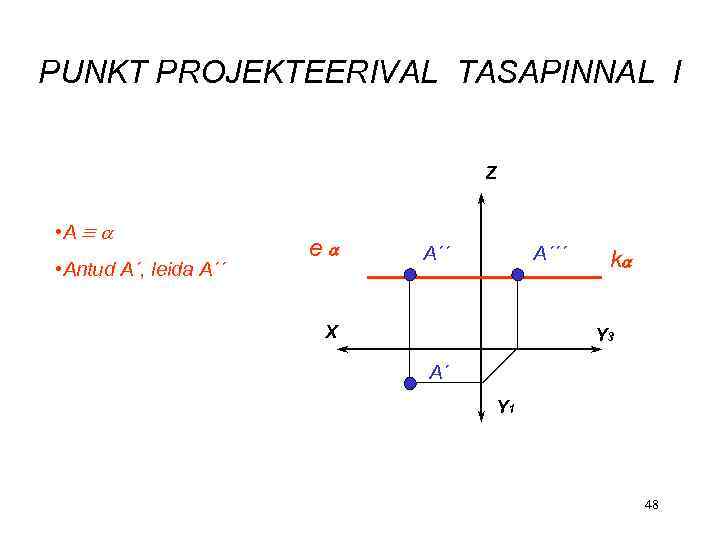PUNKT PROJEKTEERIVAL TASAPINNAL I Z • Antud A´, leida A´´ e A´´´ X k Y 3 A´ Y 1 48

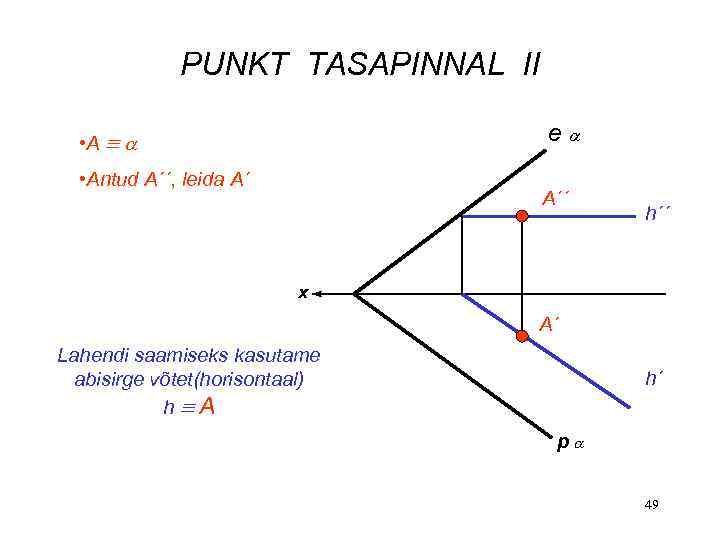PUNKT TASAPINNAL II e • Antud A´´, leida A´ A´´ h´´ x A´ Lahendi saamiseks kasutame abisirge võtet(horisontaal) h A h´ p 49

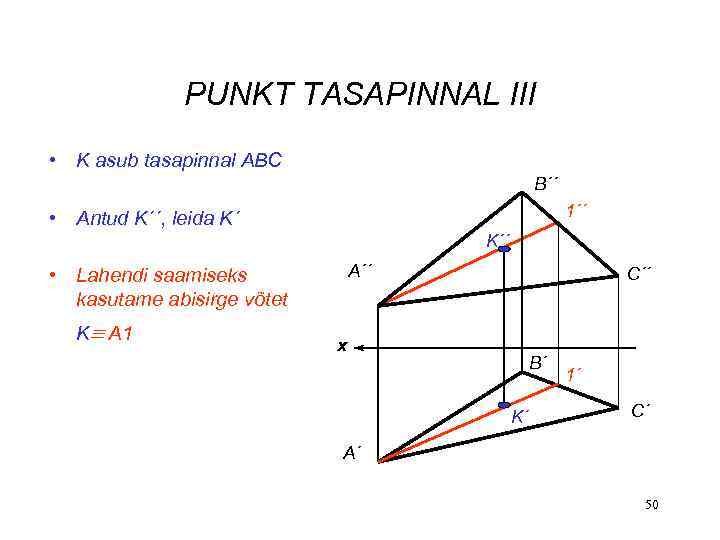PUNKT TASAPINNAL III • K asub tasapinnal ABC B´´ 1´´ • Antud K´´, leida K´ K´´ A´´ • Lahendi saamiseks kasutame abisirge võtet K A 1 C´´ x B´ K´ 1´ C´ A´ 50

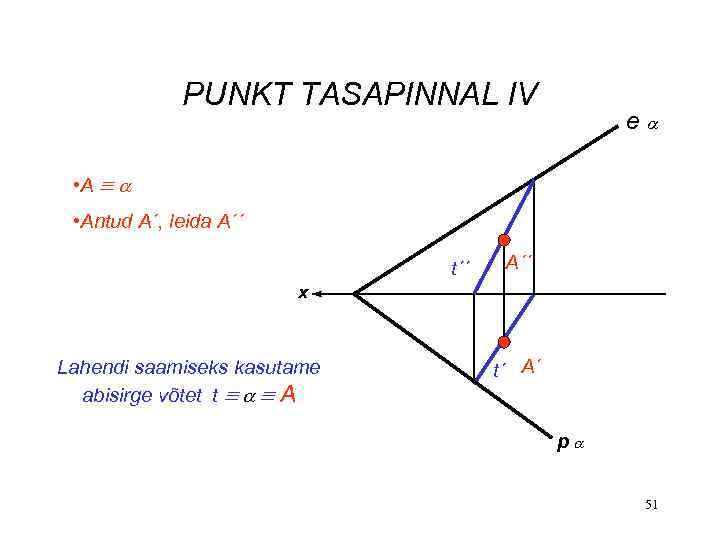PUNKT TASAPINNAL IV e • Antud A´, leida A´´ t´´ A´´ x Lahendi saamiseks kasutame abisirge võtet t A t´ A´ p 51

TASAPINDADE VASTASTIKUNE ASEND • Tasapinnad võivad ruumis olla: • paralleelsed- kui nende samanimelised jäljed on paralleelsed väljaarvatud külgekraaniga ristuvad tasapinnad • lõikuvad 52

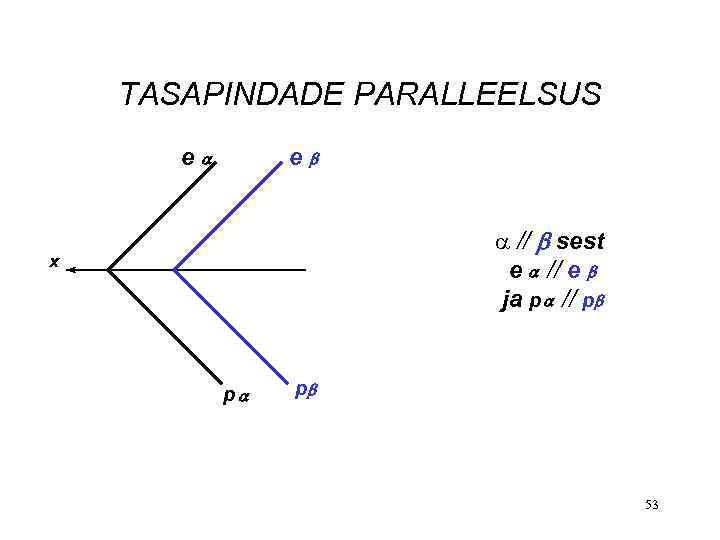TASAPINDADE PARALLEELSUS e e a // sest e // e ja p // p x p p 53

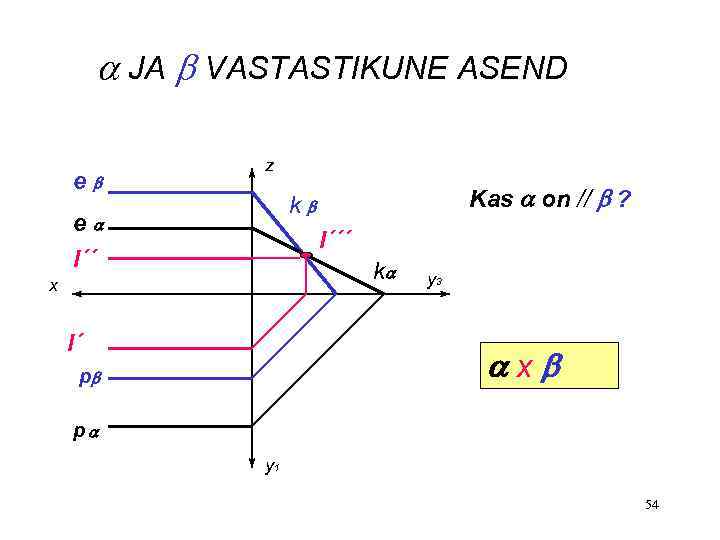JA VASTASTIKUNE ASEND e z Kas on // ? k e l´´´ k x l´ y 3 x p p y 1 54

TASAPINDADE LÕIKUMINE I e e Tasapindade jälgede lõikepunktid( E, P ) on lõikejoone jälgpunktideks E E´´ s´´ P´´ x E´ s´ p P P´ p 55

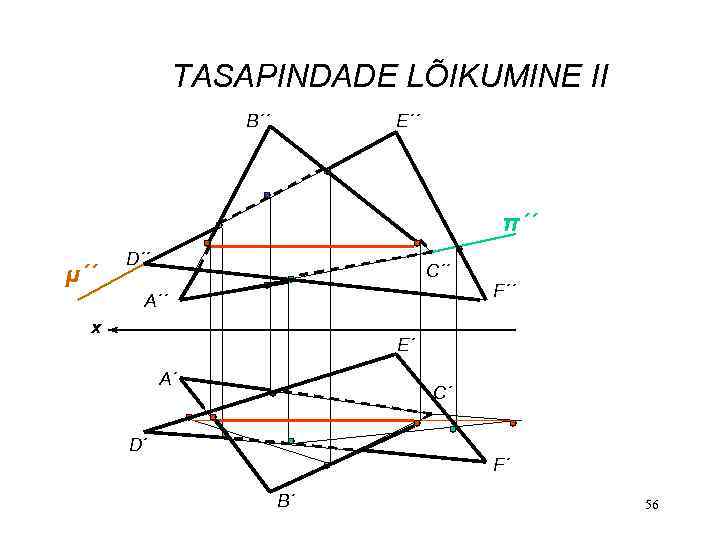TASAPINDADE LÕIKUMINE II B´´ E´´ π´´ µ´´ D´´ C´´ F´´ A´´ x E´ A´ C´ D´ F´ B´ 56

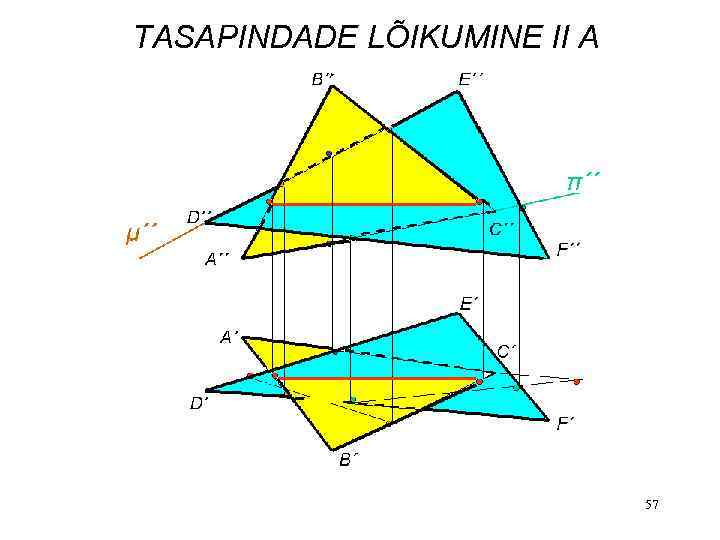TASAPINDADE LÕIKUMINE II A 57

SIRGE JA TASAPINNA LÕIKUMINE I eβ Läbi punkti A panna tasapinnale α normaal n n´ p n´´ e A´´ n´´ e L´´ x Leida normaali n ja α L´ lõikepunkti L projektsioonid β n ja ε 2 p A´ n´ pβ 58

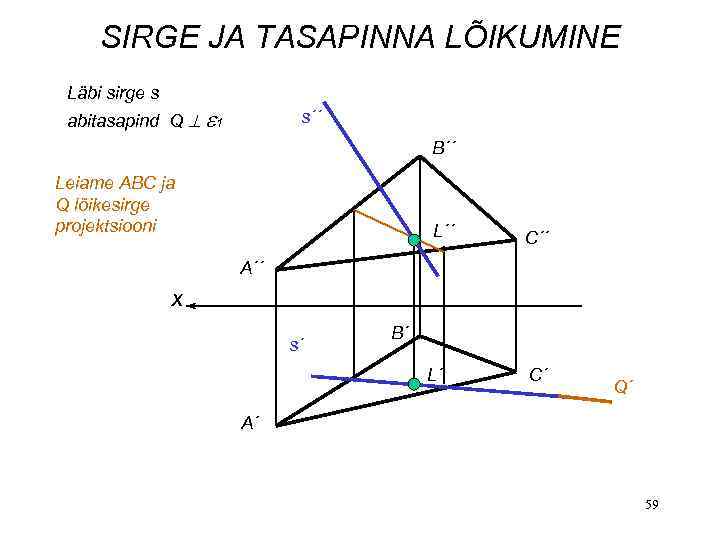SIRGE JA TASAPINNA LÕIKUMINE Läbi sirge s abitasapind Q 1 s´´ B´´ Leiame ABC ja Q lõikesirge projektsiooni L´´ C´´ A´´ x s´ B´ L´ C´ Q´ A´ 59

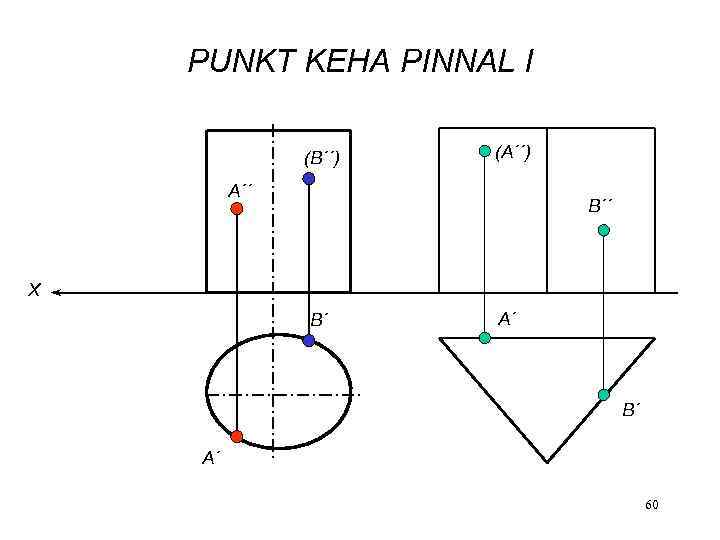PUNKT KEHA PINNAL I (B´´) (A´´) A´´ B´´ X B´ A´ 60

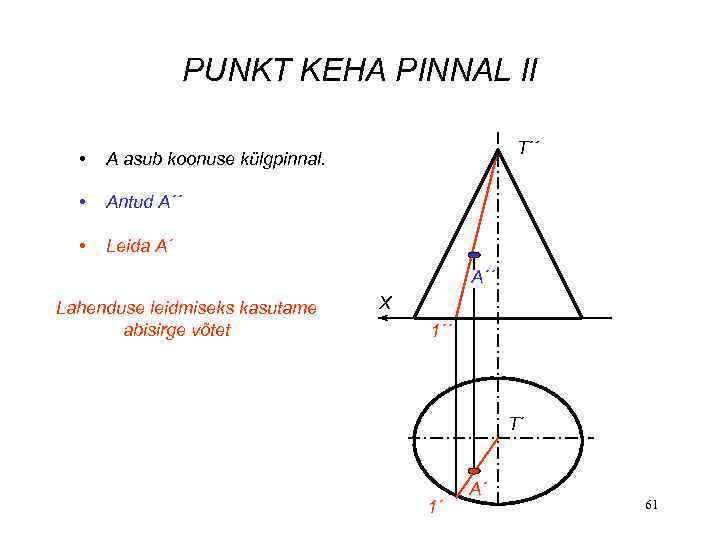PUNKT KEHA PINNAL II • • Antud A´´ • T´´ A asub koonuse külgpinnal. Leida A´ A´´ Lahenduse leidmiseks kasutame abisirge võtet X 1´´ T´ 1´ A´ 61

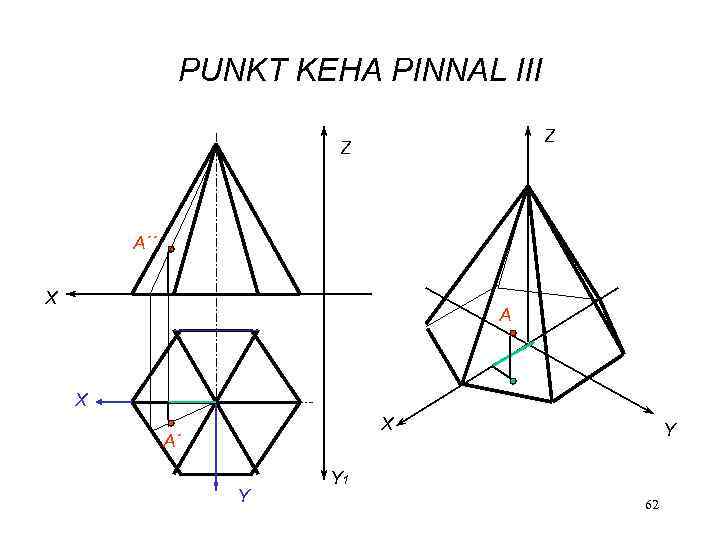PUNKT KEHA PINNAL III Z Z A´´ X A X X A´ Y Y Y 1 62

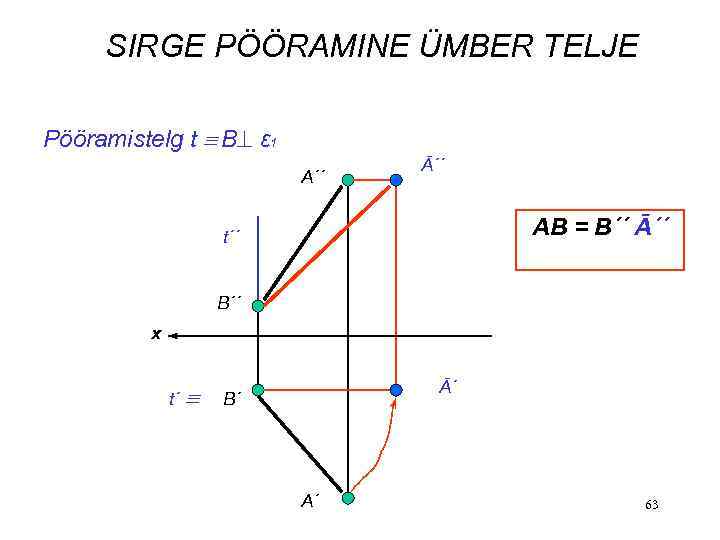SIRGE PÖÖRAMINE ÜMBER TELJE Pööramistelg t B ε 1 A´´ Ā´´ AB = B´´ Ā´´ t´´ B´´ x t´ Ā´ B´ A´ 63

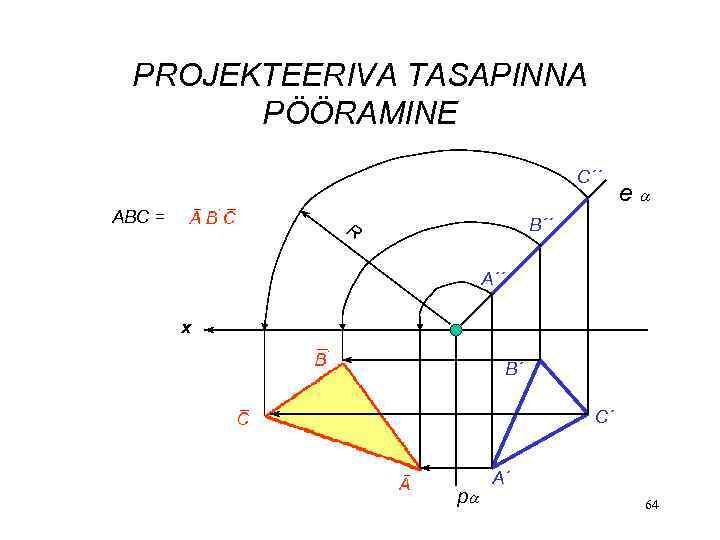PROJEKTEERIVA TASAPINNA PÖÖRAMINE C´´ ABC = e B´´ R A´´ x B´ C´ p A´ 64

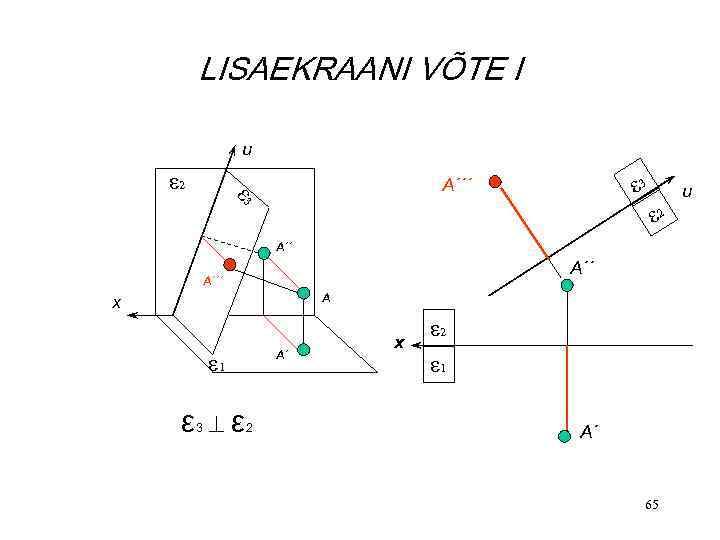LISAEKRAANI VÕTE I u ε 2 ε 3 A´´´ ε 3 u ε 2 A´´ A´´´ A x ε 1 ε 3 ε 2 A´ x ε 2 ε 1 A´ 65

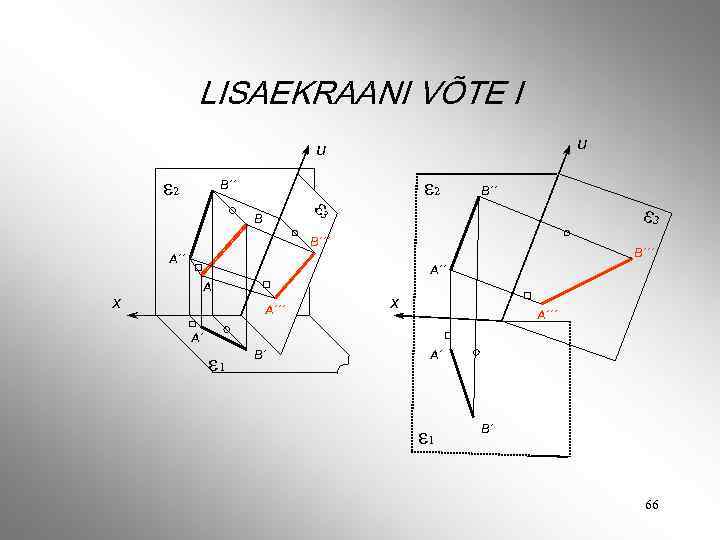LISAEKRAANI VÕTE I u u ε 2 B´´ ε 2 ε 3 B B´´ ε 3 B´´´ A´´ x A´´ A A´´´ x A´´´ A´ ε 1 B´ 66

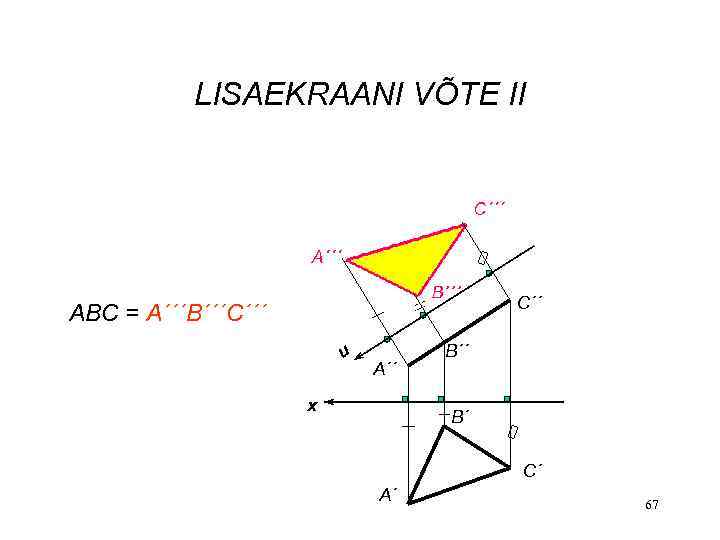LISAEKRAANI VÕTE II C´´ ABC = A´´´B´´´C´´´ u A´´ x B´´ B´ C´ A´ 67

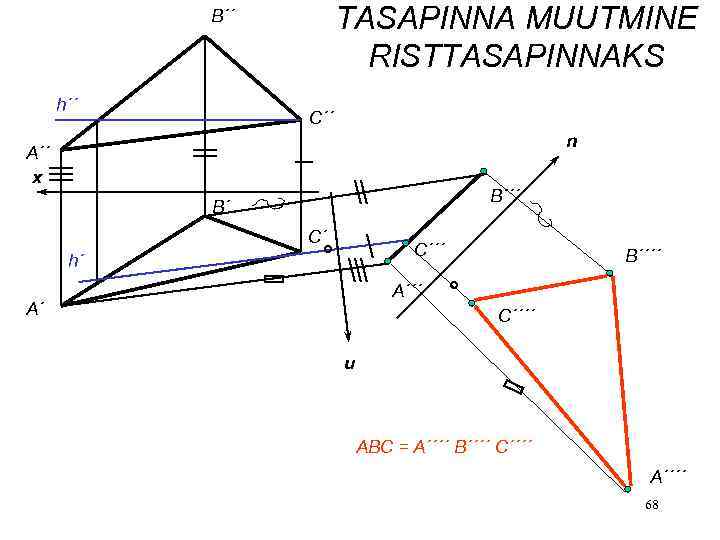TASAPINNA MUUTMINE RISTTASAPINNAKS B´´ h´´ C´´ n A´´ x B´´´ B´ C´ C´´´ h´ B´´´´ A´ C´´´´ u ABC = A´´´´ B´´´´ C´´´´ A´´´´ 68

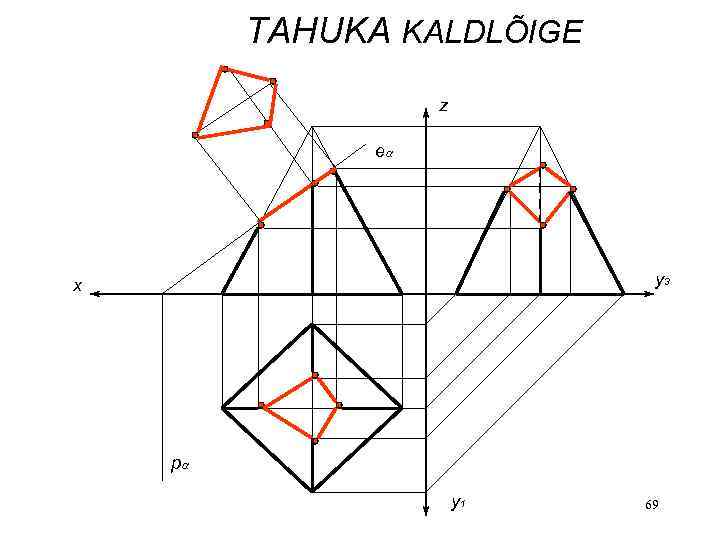TAHUKA KALDLÕIGE z e y 3 x p y 1 69

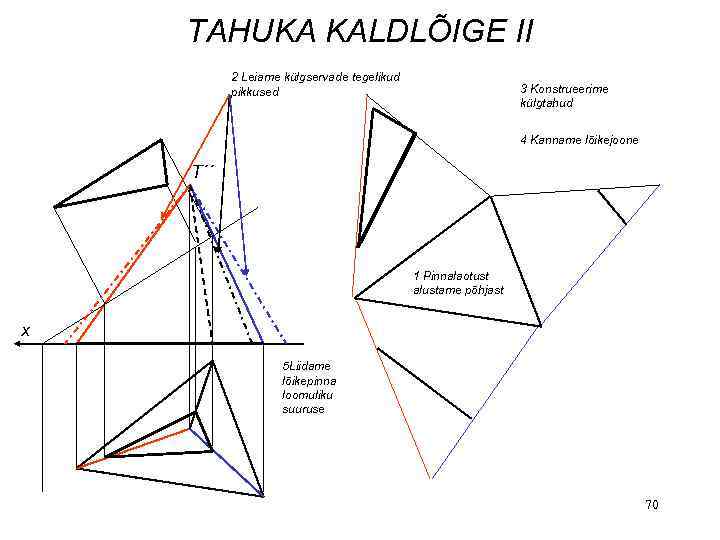TAHUKA KALDLÕIGE II 2 Leiame külgservade tegelikud pikkused 3 Konstrueerime külgtahud 4 Kanname lõikejoone T´´ 1 Pinnalaotust alustame põhjast x 5 Liidame lõikepinna loomuliku suuruse 70

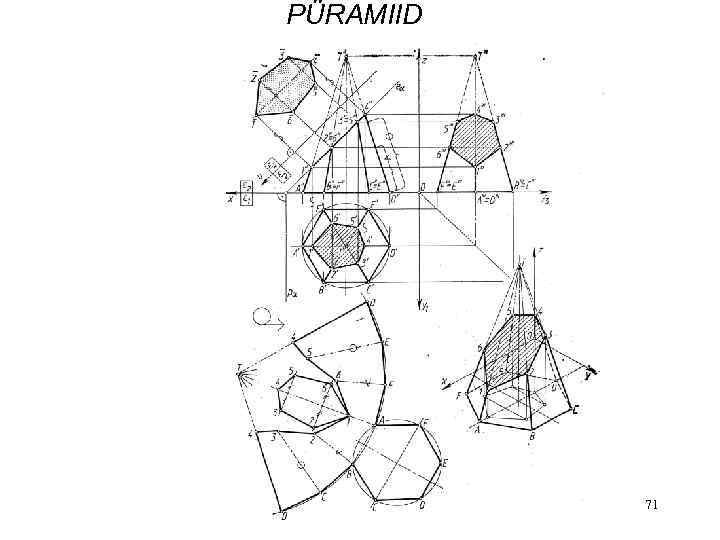PÜRAMIID 71

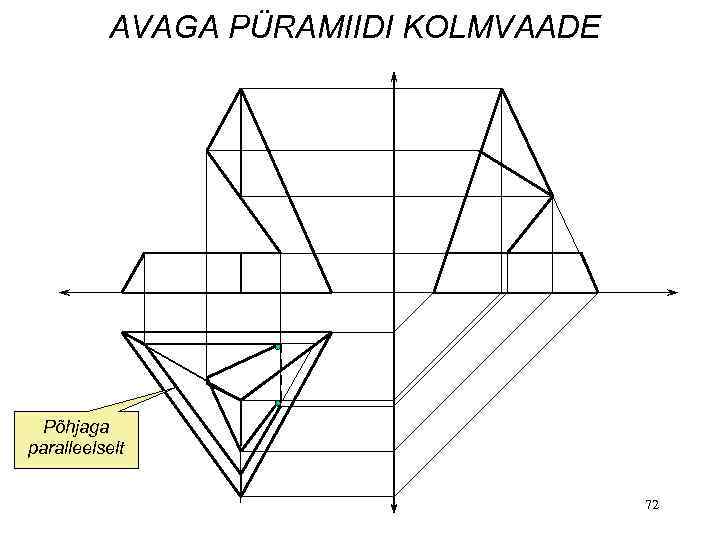AVAGA PÜRAMIIDI KOLMVAADE Põhjaga paralleelselt 72

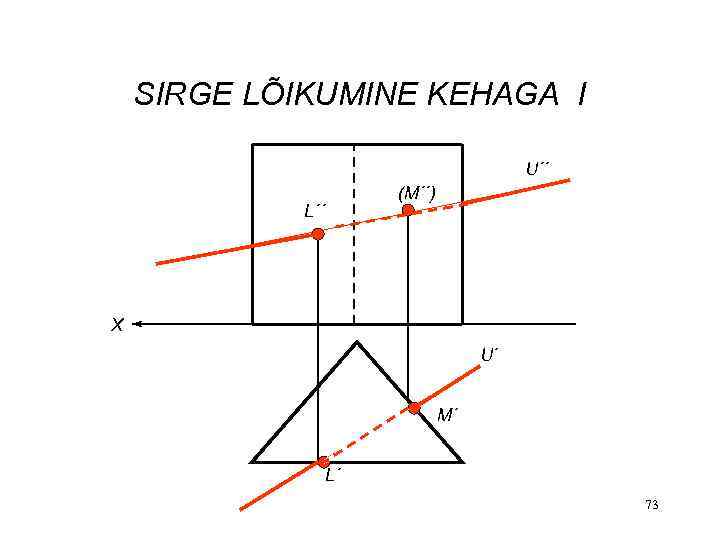SIRGE LÕIKUMINE KEHAGA I U´´ L´´ (M´´) X U´ M´ L´ 73

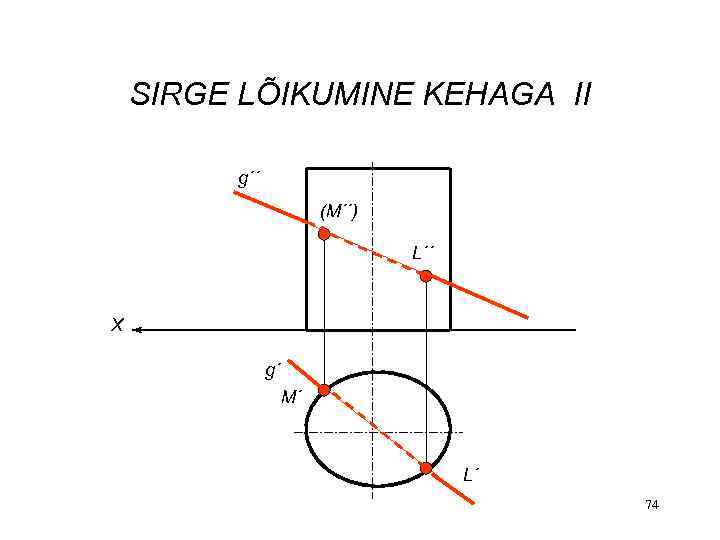SIRGE LÕIKUMINE KEHAGA II g´´ (M´´) L´´ X g´ M´ L´ 74

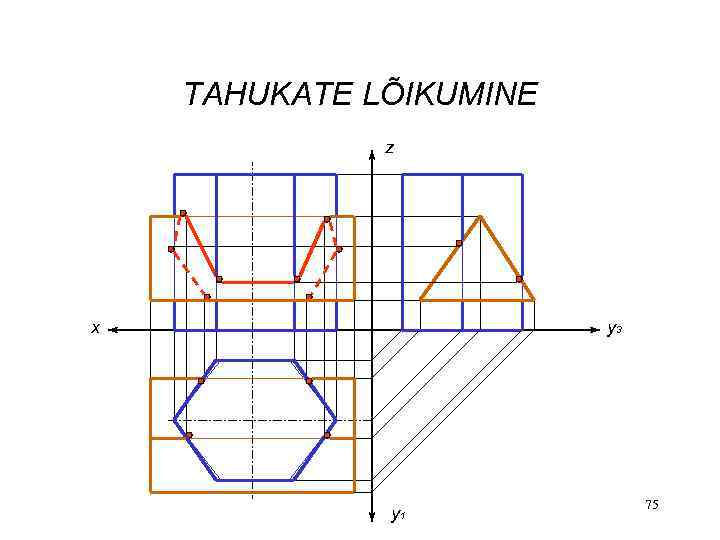TAHUKATE LÕIKUMINE z x y 3 y 1 75

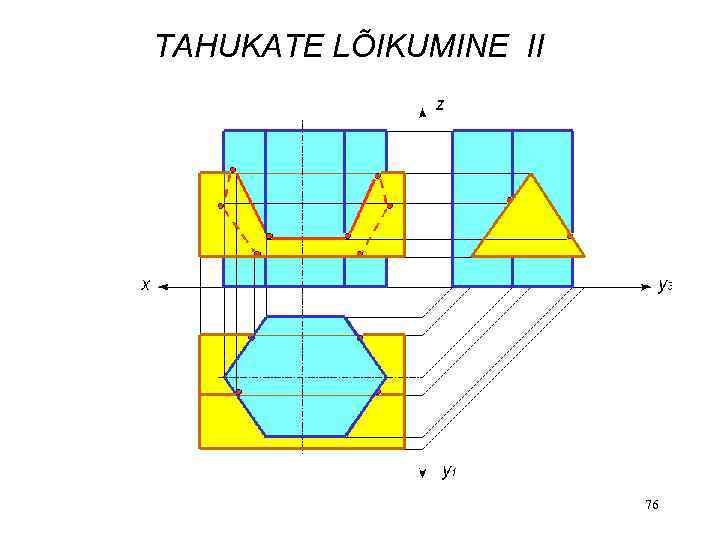TAHUKATE LÕIKUMINE II 76

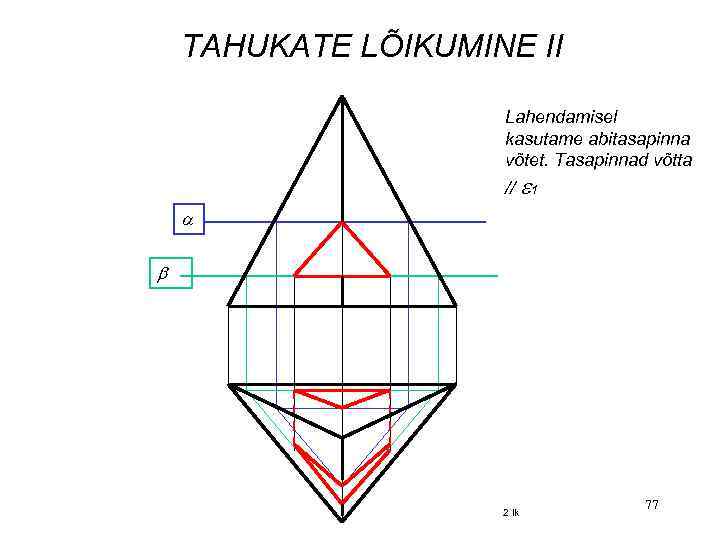TAHUKATE LÕIKUMINE II Lahendamisel kasutame abitasapinna võtet. Tasapinnad võtta // 1 2 lk 77

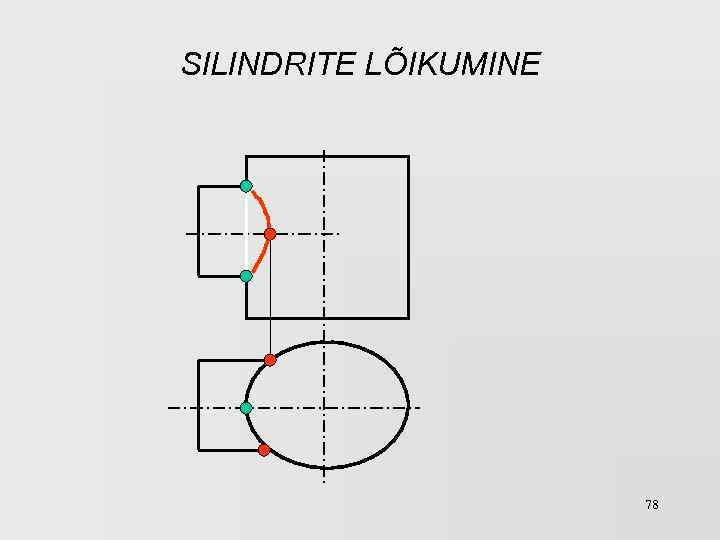SILINDRITE LÕIKUMINE 78

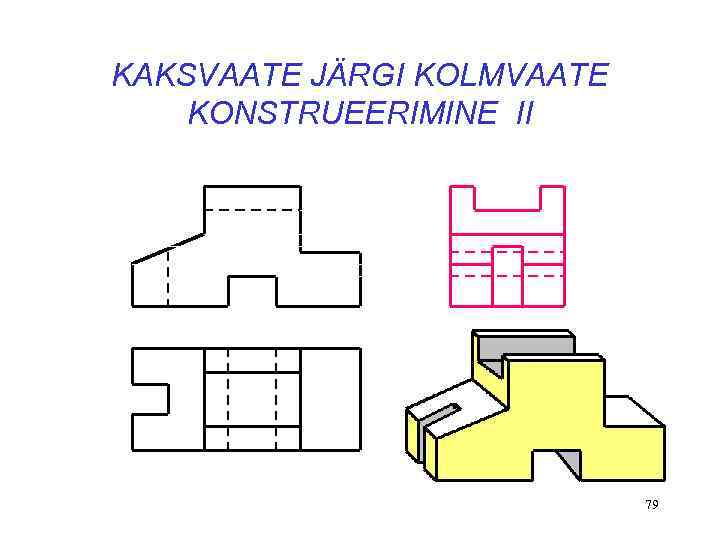KAKSVAATE JÄRGI KOLMVAATE KONSTRUEERIMINE II 79

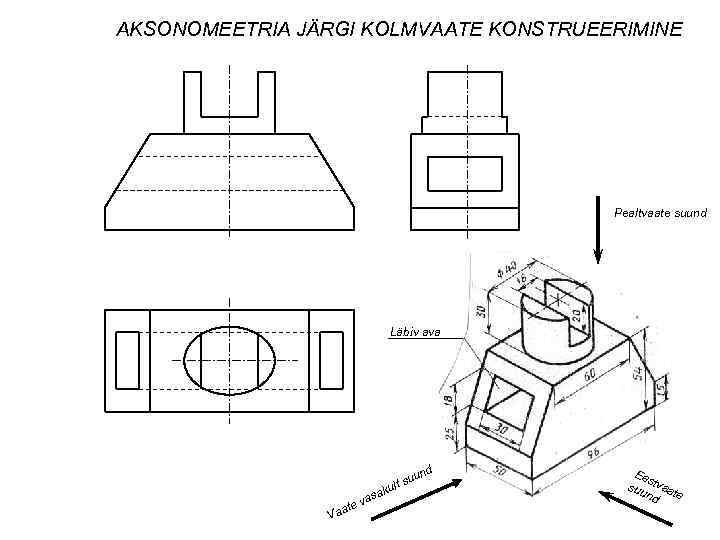AKSONOMEETRIA JÄRGI KOLMVAATE KONSTRUEERIMINE Pealtvaate suund Läbiv ava d ku uun lt s V asa te v aa Ee s suu tvaa nd te