Team Members Clement Hudson —Tularosa High School Albert

Team Members Clement Hudson --Tularosa High School Albert Simon -- Alamogordo High School Margaret Suzukida--Alamogordo High School Clare Riker Tinguely--Alamogordo High School

THE QUEUEING THEORY Tulie Basin Dream Team Alamogordo and Tularosa High Schools

Executive Summary • Queueing Theory - mathematical technique cin >> • Low traffic intensity - # of customers is low • Bursty process - long queues build up cout << • Output - analysis of scheduling matrices

Problem Statement • Standing in line (queue) = fact of life! • Managers need a way to optimize scheduling of employees • Program results in a number assigned to Time in system AND Time in Queue Number of customer in line AND in system based on arriving and exiting

Secondary Other Services customers Wait for service External Numbers exiting into system Schedules employees Numbers coming into system

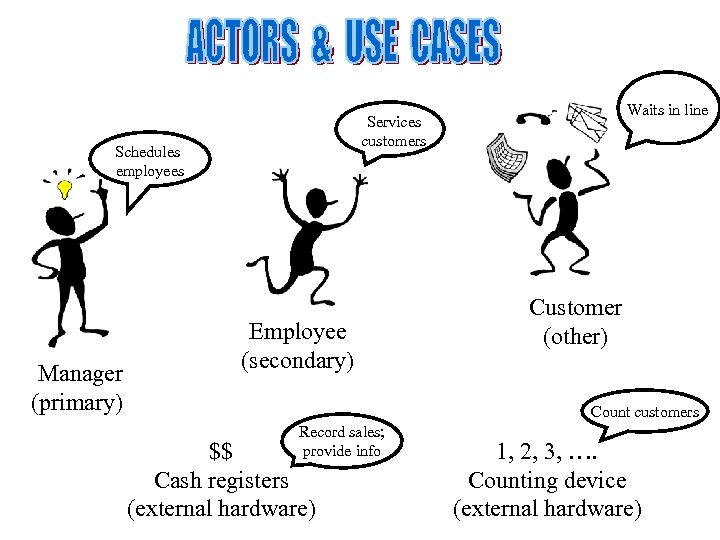
Schedules employees Manager (primary) Waits in line Services customers Employee (secondary) Customer (other) Count customers Record sales; provide info $$ Cash registers (external hardware) 1, 2, 3, …. Counting device (external hardware)

EMPLOYEES Not a singleton. Entity because they are within the modeled system. Behaviors: Service customers; follow a schedule. CUSTOMERS Not a singleton. Boundary because they enter into business from outside and determine queue lengths. Behaviors: Determine length of queue. QUEUE Not a singleton. Entity because they are within the modeled system. Behaviors: Length determined by no. of customers. MANAGER Singleton. Boundary because they enter into business from outside to only review numbers for scheduling. They will probably not be programmed. Once the program is in place, you may not need a manager! Behaviors: Schedules employees.

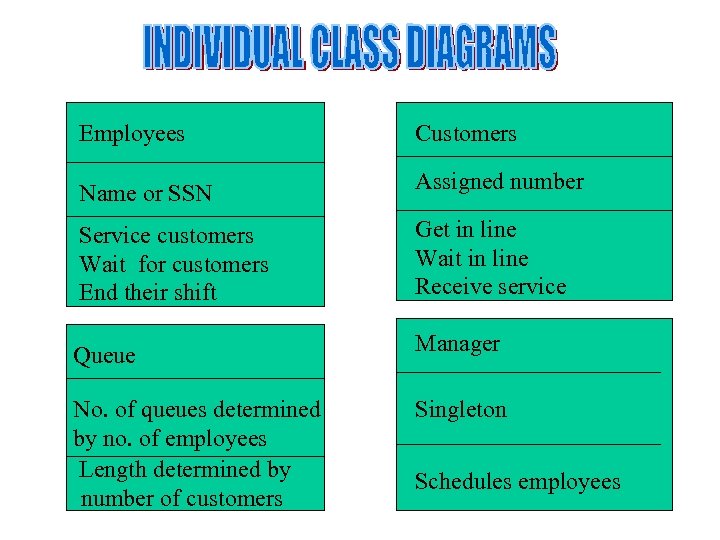
Employees Customers Name or SSN Assigned number Service customers Wait for customers End their shift Get in line Wait in line Receive service Queue Manager No. of queues determined by no. of employees Length determined by number of customers Singleton Schedules employees

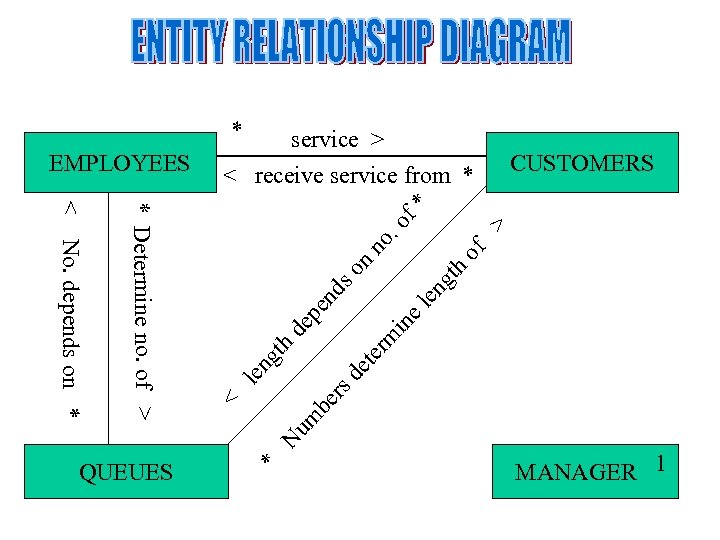
* f* > . o of no th n in el en g so rs de te rm en d de p h ng t le um be * N No. depends on * * Determine no. of > < QUEUES CUSTOMERS < receive service from * < EMPLOYEES service > MANAGER 1

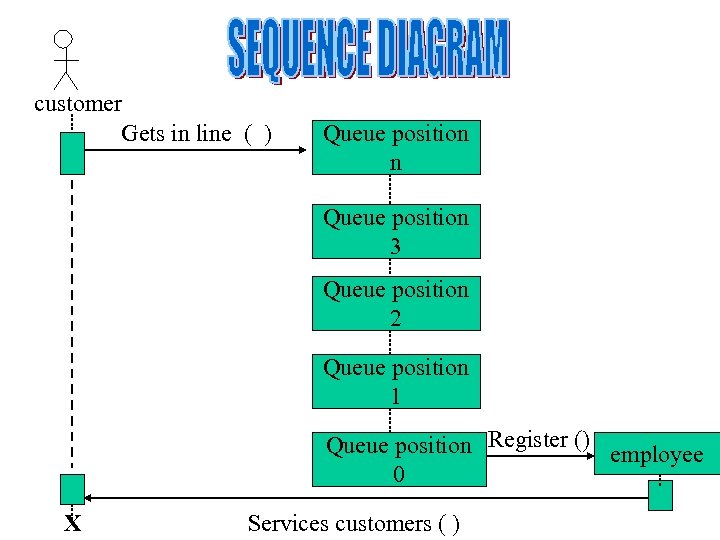
customer Gets in line ( ) Queue position n Queue position 3 Queue position 2 Queue position 1 Queue position Register () employee 0 X Services customers ( )

EMPLOYEE [No customers] [Customers appear or leave] [Customers are present] Waiting for Customers Servicing Customers f do [End of Shift] Ending of Shift n [E S ] ift h

CUSTOMER [Moving Ahead] [No purchasing] Getting in line Receiving Service [Front of queue] Waiting [Front of queue] [Purchasing] [Leaving]

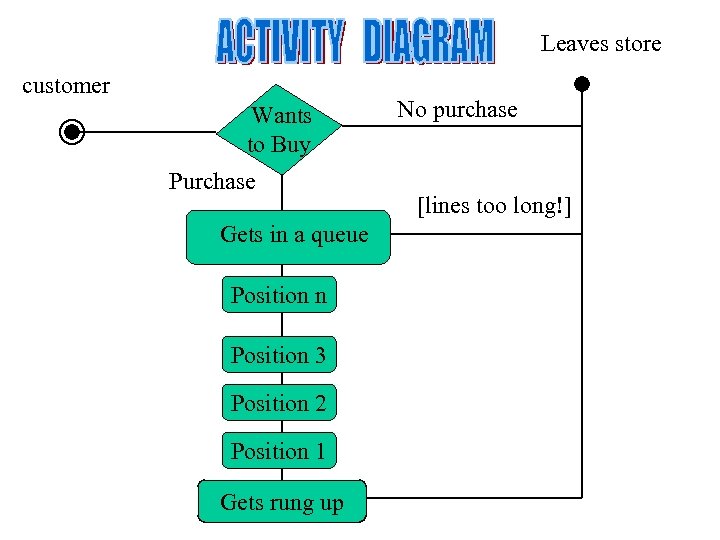
Leaves store customer Wants to Buy Purchase Gets in a queue Position n Position 3 Position 2 Position 1 Gets rung up No purchase [lines too long!]

Method • Code performs a summation using a loop until the numbers converge or diverge • C++, Markovian equations, Poisson arrival equations • Computes such statistics as: time customer spends in the queue and in the system, expected line length and no. of customers

Variables - 1 • • µ n • p(0) = • p(n) = arrival rate service rate traffic intensity ( / µ ) [< 1] number of customers in system (queue + service) steady state probabilities 1 - (1 - ) ( ^ n), n = 1, 2, 3….

Variables - continued W(q) = expected time in queue E [ time in queue] / [ ( -1)] = time in system E [time in system] 1 / ( - ) = line length E[line length] ^ 2 / [ ( - )] = Number of customers E[number in system] / ( - ) W W L (q) L L L

(q) (w) ln Variables - continued percentile high percentiles for time in queue high percentiles for time in system the natural logarithm (q) [90] = W * ln (10 * ) (q) [95] = W * ln (20 * ) (w) [90) = W * ln (10) (w) [95] = W * ln (20)

Original Achievement • Meeting the challenge of doing the project in two weeks • Very useful in understanding what our students experience • Outcomes from the queueing calculations may help in lessening waiting times

Strengths and Weaknesses • Weaknesses: – Time constraints; project can be expanded to look at other scenarios. – Poisson arrival rate - exponential – Deterministic • Strengths: Team-building skills which resulted from cooperative learning environment of the class.

Results of Our Program • Using a series of math formulae, enhance decision-making processes for employee scheduling • M/M/1 steady state model • Wq, W, Lq, L were calculated to give time in a queue, time in system, line length, and number in system

Conclusions • Organizations are ubiquitous. • Anytime you are serviced, you must queue. • We wanted to know what happened during peak periods (high traffic intensity) in order to properly schedule employees. • The program outputs expected length of queue, time in system, length of line (hours), and the amount of time waiting to be serviced.

Resources/Bibliography Bolch, G. , Greiner, S. , de Meer, H. , and K. S. Trivedi. (1998). Queuing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications. Davis, William S. and Yen, David C. (1999). Systems Analysis and Design: Information System Consultant’s Handbook. Enns, S. T. (1999). A simple spreadsheet approach to understanding work flow in production facilities. Total Quality Management. Glass, Victor and Cahn, Ellen S. (1997). A queueing model of organization structure. Journal of Business and Economic Studies 3, 13 -28. He, Qu-Ming & Marcel F. Neuts. (1997). On Episodic Queues. Society for Industrial and Applied Mathenatucs. Robertazzi, Thomas G. (1994). Computer Networks and Systems: Queueing Theory and Performance Evaluation. Standard Template Library. (1999). http: //www. la. unm. edu: 8001/cs 259/stl_doc/

Many Thankx!!! • Nolan Gray, Mike Fisk, Shaun Cooper • for support and because they’re the judges : ). • NMSU & LANL for venue, labs & $$$$. especially: and • Karin, Sharon, Chris, Gina, and David without whom this extraordinary fun would not have been possible. • All the little people (students), and Miles, too, with whom we now empathize and who will provide the coding to the next generation’s problems. We can now help them more intelligently.