Teaching Mathematics What the Research Says A Sample

Teaching Mathematics What the Research Says: A Sample or Three

Expert Panel Reports • 30 Years of Research • The Same Message at all levels: K-12 • Drives the training, the resources • Summary provided (by me)

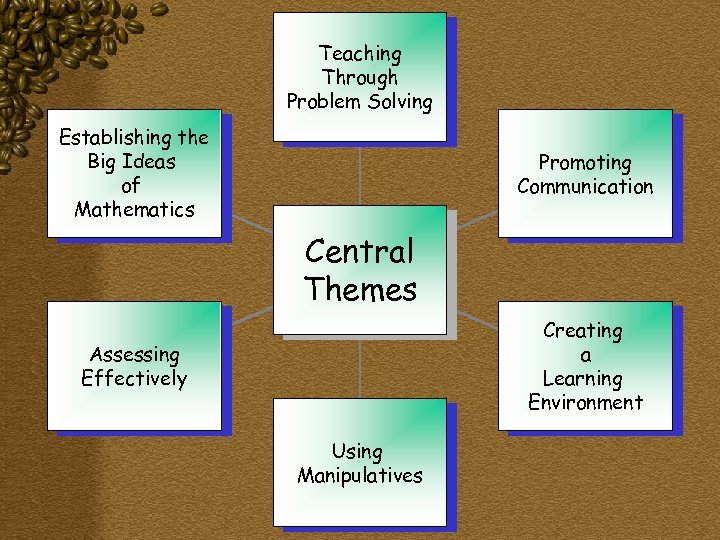Teaching Through Problem Solving Establishing the Big Ideas of Mathematics Promoting Communication Central Themes Creating a Learning Environment Assessing Effectively Using Manipulatives

Teaching Through Problem Solving • the reason for math to exist • nobody does a sheet of math for fun • 3 part lesson 1) pose & discuss problem 2) students solve the problem 3) debrief • See New Curriculum Sample

Problem solving … mainstay of mathematical instruction.

Creating a Learning Environment • 50% of the population suffer from math anxiety or math avoidance • teachers teach as they have been taught • mistakes are opportunities to discuss & learn (see communication) • take risks (see above) • arithmetic has one answer but mathematics has multiple solutions

Creating a Learning Environment • children come to school as natural mathematicians – we beat it out of them • equity means each child has the right to be taught with methods that are most effective for them • at risk students learn best in a problem solving environment full of talk and communication

Promoting Communication • students must speak to learn • a predominately silent math classroom is one where learning has been minimized • students can only write if they have been in a classroom where they have talked and listened • a math problem is the most complex text to read • math is where hands-on learners are successful – the perfect place to start reading & writing

Establishing the Big Ideas of Mathematics • teaching mathematics around central concepts – not as a checklist of skills • understanding to create proficiency • Big Ideas of Number Sense counting quantity operational sense (relationships) (representation) proportional reasoning (Junior +) • See New Curriculum Sample

Using Manipulatives • modeling mathematics through concrete materials and digital technology • an effective method to create understanding for all students – nothing to do with ability • essential for some learners • count the references to concrete materials in the Grade 3 number sense

Assessing Effectively • main purpose of assessment to create learning (formative & feedback) • focused observation is the most effective tool and is the predominate tool for assessment and evaluation in the primary division • variety of tools (observations, performance tasks, journals, portfolios, investigations, selfassessment, tests (Gr. 3 & up) • only assign a grade or mark for summative tasks – grades do not increase learning

Expert Panel Reports Summary • Positive Learning Environment – – – the learner the classroom environment equity home connections special needs/at risk scheduling – teachers • Problem Solving Process – problem solving – making connections – lesson design • All Learning Involves Communication – communication – language • The Big Ideas of Math – Big Ideas – Algorithms & Formulas • Learning Tools – concrete material – digital technology • Assessment for Learning – assessment

Sample Lesson Think-Pair-Share Think: How would you add these numbers? 24 36 48 72 Pair: 1. With your partner (group), discuss how you added the numbers. 2. Record the different methods in your group journal. (Pictures, numbers, words)

Sample Lesson Think-Pair-Share: Go to the front and share your groups solutions with the class. In you journal: Describe your favourite method and one other person’s method of adding these numbers.

Look to the Numbers!

Early Primary Samples

Tell me what you know about 5. (Diagnostic – Week 1 Grade 1) 5

Tell Me About “ 5”

One More Than/Two More Than Facts This strategy covers 36 basic facts. They have either an addend of 1 or 2. 8 + 2 more 3 + 1 more

How many squares?

How Many?

How many squares?

How Many?

How many squares?

How many squares?

How Many?

5 One More Than

Two More Than Let’s try two more for the following dot plates.

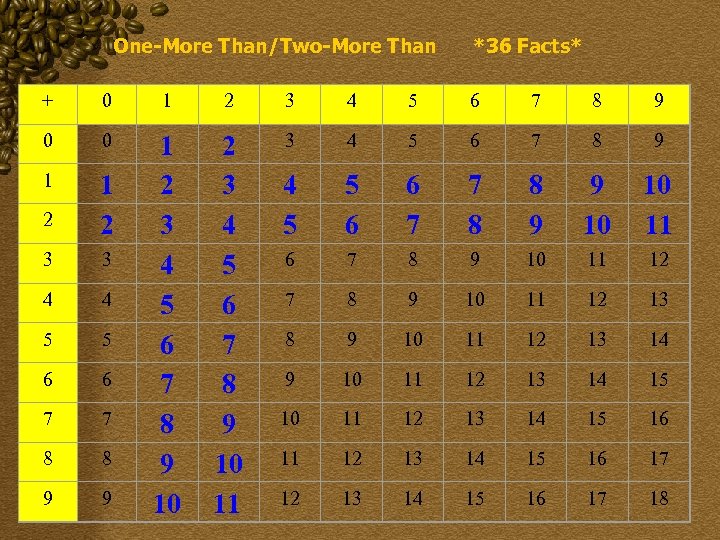One-More Than/Two-More Than *36 Facts* + 0 1 2 3 4 5 6 7 8 9 0 0 4 5 6 7 8 9 2 1 2 4 5 5 6 6 7 7 8 8 9 9 10 10 11 3 3 6 7 8 9 10 11 12 4 4 7 8 9 10 11 12 13 5 5 8 9 10 11 12 13 14 6 6 9 10 11 12 13 14 15 7 7 10 11 12 13 14 15 16 8 8 11 12 13 14 15 16 17 9 9 2 3 4 5 6 7 8 9 10 11 3 1 1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18

Facts to 10 • • • Use 10 Two-Colour Counters Shake them in your hand Drop them Place them on the 10 -Frame Write a number sentence to represent this remove the reds from yours and your partner’s. Add the yellows using the frames • You can do this for any number

How Would You Add These? How Would You Subtract These? How many dots in all? What is the difference between the number of dots on these two plates?

Morgan has 7 apples. Jesse has 9 apples. How da ya like dem apples? • • • show using counters and no frames show using counters with frames show using a numberless number line show using abstract numbers show using distributive property to demonstrategies • Why did I choose 7 and 9?

Hundreds Chart 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

A Better Hundreds Chart

De-Brief – Grade 2 Last time for Pizza Day we ordered 37 slices of pizza. This time we need to order 13 more slices. How many pieces of pizza do we need to order?

Late Primary/ Early Junior Samples

Race to 100 Race to 0

Why is this space here?

How do you teach “Long Division”

Create an Array to Represent: 2 x 3

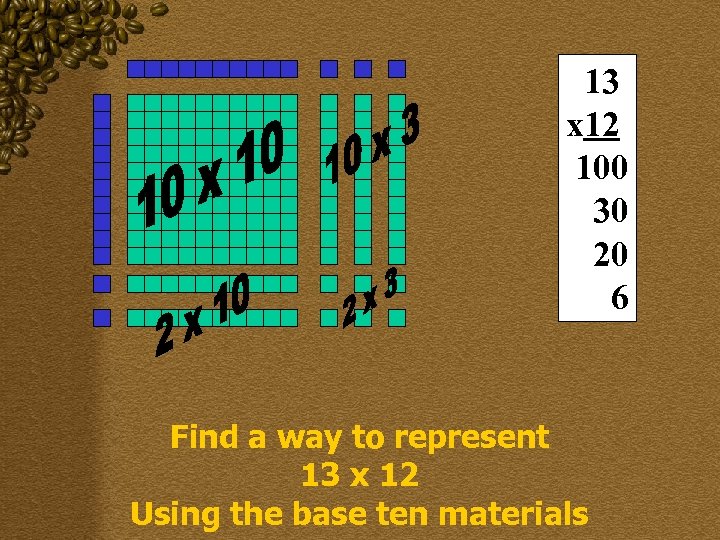13 x 12 100 30 20 6 Find a way to represent 13 x 12 Using the base ten materials

Open Arrays doubling & halving • 10 X 13 • 2 X 13 • 12 X 13 • 6 X 26

Open Arrays doubling & halving • • • 6 x 8 12 x 16 24 x 16 12 x 32 6 x 64

Open Arrays doubling & halving (x 2, /2) • 7 x 7 • 3½ x 14 • a similar strategy (no paper allowed) • 8 x 4 • 0. 08 x 400

Late Junior

The lesson takes place in a Grade 5 classroom towards the end of the school year. Ms. H teaches a class with a wide range of abilities, both in mathematics and literacy. In the first phase of the lesson Ms. H poses an opening problem for a unit on division: “I have a problem. I have a jar which I know held 317 marbles when it was full. As you can see, it is empty, and I want to fill it full of marbles again. At my corner store I can buy small bags of marbles, with 23 marbles in a bag. ” She holds up the jar and the small bag of marbles. “I want to go to the store and buy enough bags but no extras. How many bags should I buy? ”

Ms. H has not yet taught a standard algorithm for division, although a few students have seen it at home. Rather than going through the steps of division, students talk about the problem and look at the jar and the small bag of marbles. Then they return to their seats to work in pairs. Each pair has a jar and a small bag of 23 marbles.

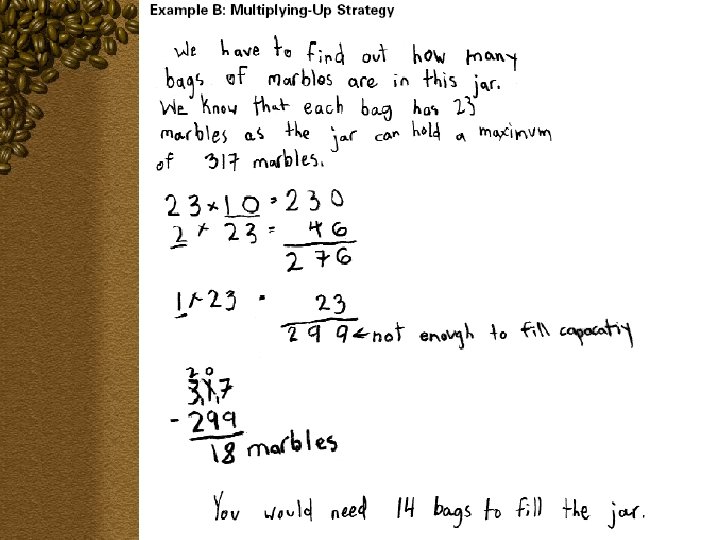
Math Quiz

Math Quiz 81

There are 134 different subtraction algorithms internationally • Research clearly shows that effective math instruction has students creating their own “algorithms” (see Grade 3 Number Sense) • Discussing and listening to others algorithms • Examining “standard’ algorithms • When professional mathematicians are given computation questions: 95% do not use standard algorithms. • Look to the numbers & use strategies!

Fractions (Proportional Reasoning)

Tangram Exploration

Tangram Peanut Brittle The “Dentists Love Us” candy company has decided to produce “top-of-the-line” peanut brittle. A full square of brittle costs $3. 20. But you can buy a tangram piece for a proportional amount. How much would you pay for each type of tangram piece. Be prepared to explain whether you used fractions, decimals, division, or some other method.

Hypothesis: The formula for area of a trapezoid is in fact a generalized formula for the area of all triangles and quadrilaterals. Demonstrate this for all triangles and quadrilaterals. (or determine how many cases it holds true for) Prove algebraically. (Or prove for as many cases as it holds true for) Area of Trap = (a + b) h 2

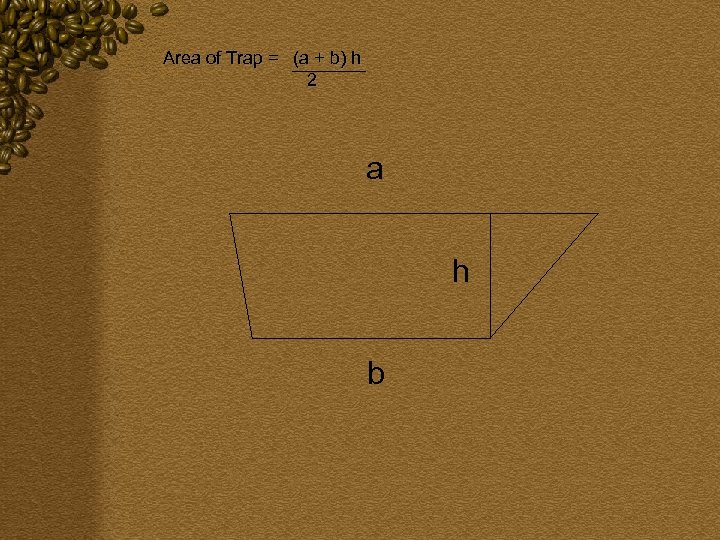Area of Trap = (a + b) h 2 a h b

Forward to the New Basics There is a difference between being a dedicated caring teaching and being an effective teachers. Dedication and care is the prerequisite that is necessary to be a teacher. Effective starts with caring but only progresses with research-based methods and techniques.

Forward to the New Basics We are the only profession where a practitioner of 100 years ago would recognize most of what goes on in most situations today. This is a major cultural shift. (Remember that term “Paradigm Shift”?

Forward to the New Basics Drive by in-service will not create the shift.