ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА. ОБРАБОТКА РЕЗУЛЬТАТОВ ТАХЕОМЕТРИЧЕСКОЙ СЪЕМКИ. ЭЛЕКТРОННЫЕ ТАХЕОМЕТРЫ.


ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА. ОБРАБОТКА РЕЗУЛЬТАТОВ ТАХЕОМЕТРИЧЕСКОЙ СЪЕМКИ. ЭЛЕКТРОННЫЕ ТАХЕОМЕТРЫ. РЕЛЬЕФ, ФОРМЫ РЕЛЬЕФА И СПОСОБЫ ЕГО ИЗОБРАЖЕНИЯ. ГОРИЗОНТАЛИ. ЛИНИИ УКЛОНА. ГРАФИКИ ЗАЛОЖЕНИЯ. ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА. Целью тахеометрической съемки является получение топографического плана местности. В теодолитно – тахеометрических ходах отметки вершин получают путем тригонометрического нивелирования, а стороны измеряют нитяным дальномером. По инструкции при съемке рельефа через два или более метров допускается определение высот пунктов тригонометрическим нивелированием, а при съемке рельефа с сечением до 1 метра только геометрическим. Съемка контуров и рельефа с пунктов (станций) выполняется, как правило, полярным способом. При этом одно наведение на рейку, установленную на точке местности, позволяет получить расстояние, направление и превышение, по которым определяются пространственные координаты этой точки.

Согласно инструкции тахеометрическая съемка применяется как основной вид съемки для создания планов небольших участков, или в сочетании с другими видами съемок, когда: А. Применение других видов съемок не целесообразно. Б.Выполняется съемка рельефа на застроенной территории. В. Выполняется съемка узких полос местности при изысканиях линейных сооружений. Последовательность работ на станции при проложении теодолитно-тахеометрических ходов следующая: А. Измеряют полным приемом горизонтальные углы между направлениями на смежные станции. Б. Измеряют при КЛ и КП углы наклона. В. Измеряют дальномером расстояния между станциями

Значения места нуля, углов наклона и дальномерные расстояния определяют для каждой станции и линии хода дважды – в прямом и обратном направлениях. В результате вычислительной обработки полевых данных, полученных при проложении тахеометрических ходов, должны быть определены координаты и отметки их вершин. Вычисление координат вершин определяется по правилам теодолитной съемки. Горизонтальные проложения линий вычисляются по данным замеров дальномером. Превышения обычно вычисляются по тахеометрическим таблицам или по формуле h= d · tgγ + ί + l + f ; где d – горизонтальное проложение, ί – высота прибора, l – высота вешки (рейки), f – поправка за кривизну земли и рефракцию света, она учитывается при d > 300 м. ί γ h l d А С В D

ί γ h l d А С В D При ί = l и f = 0 превышение находим по формуле h = d · tgγ, для этого измеряется высота прибора и на рейке делается отметка равная высоте прибора.
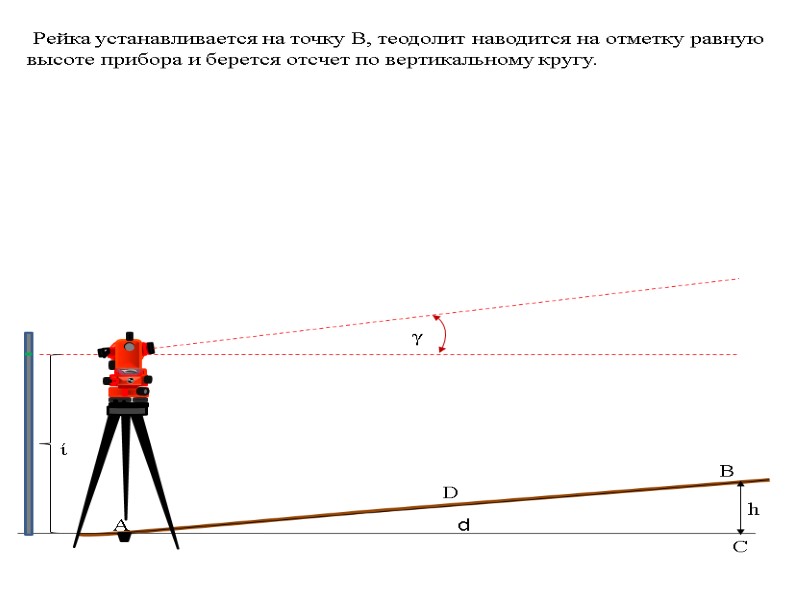
ί γ h d А С В D Рейка устанавливается на точку В, теодолит наводится на отметку равную высоте прибора и берется отсчет по вертикальному кругу.

ί h d А С В D
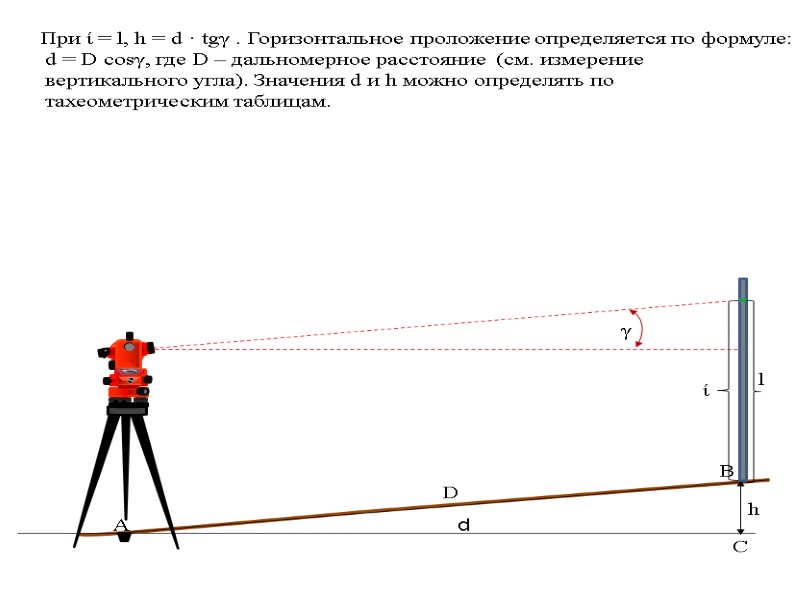
ί h d А С В D l При ί = l, h = d · tgγ . Горизонтальное проложение определяется по формуле: d = D cosγ, где D – дальномерное расстояние (см. измерение вертикального угла). Значения d и h можно определять по тахеометрическим таблицам. γ

Порядок работы на станции при съемке ситуации следующий. Например: необходимо определить положение нескольких точек со станций l и ll , тахеометрического хода. Устанавливаем теодолит на станции l, приводим его в рабочее положение и замеряем высоту прибора с точностью до 1 см. На рейке делаем отметку равную высоте прибора.
l ll

l ll Устанавливаем рейку на станцию № ll и определяем место нуля вертикального круга.
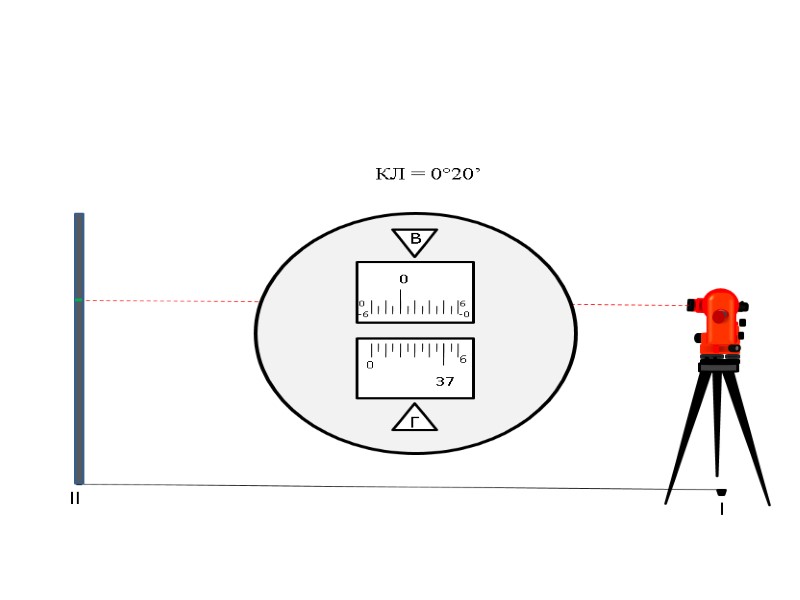
l ll КЛ = 0°20’

l ll Переводим трубу через зенит и берем отсчет при круге «право».

l ll

l ll

l ll

l ll

l ll

l ll
l ll

l ll

l ll
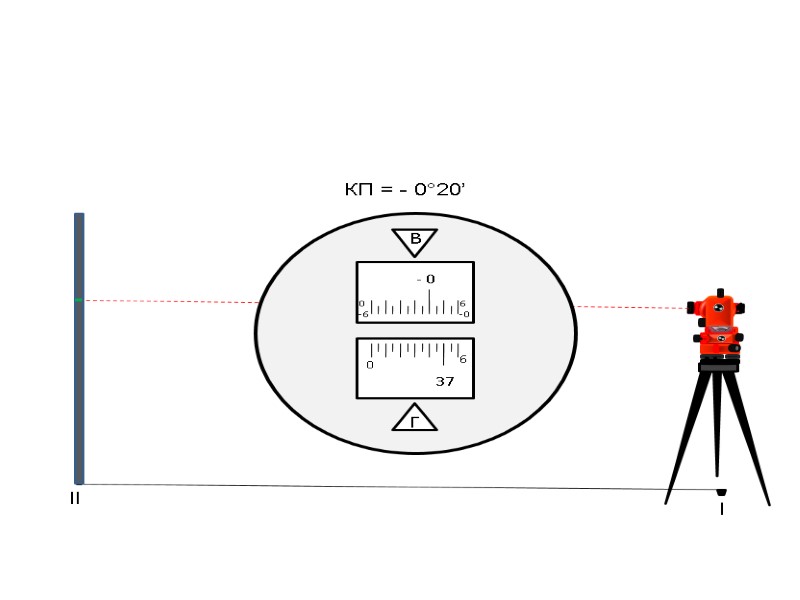
l ll КП = - 0°20’
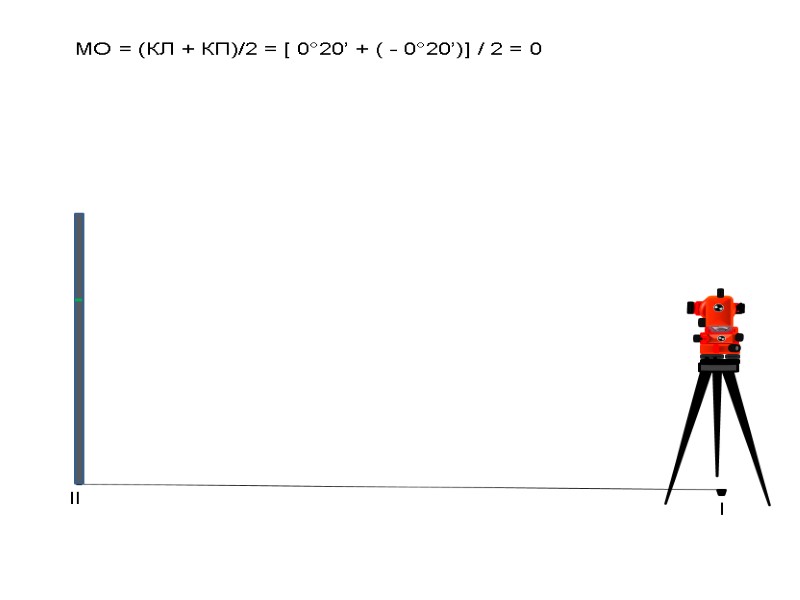
l ll МО = (КЛ + КП)/2 = [ 0°20’ + ( - 0°20’)] / 2 = 0
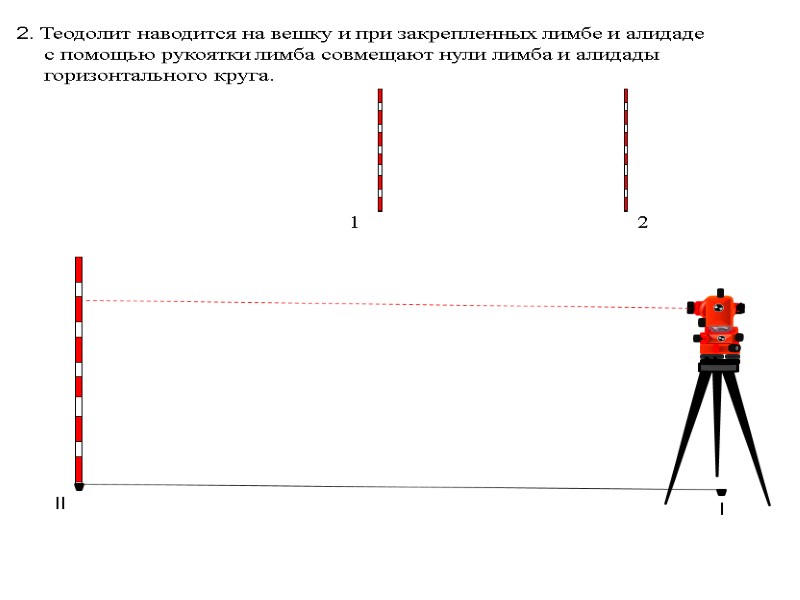
l ll 2. Теодолит наводится на вешку и при закрепленных лимбе и алидаде с помощью рукоятки лимба совмещают нули лимба и алидады горизонтального круга. 1 2
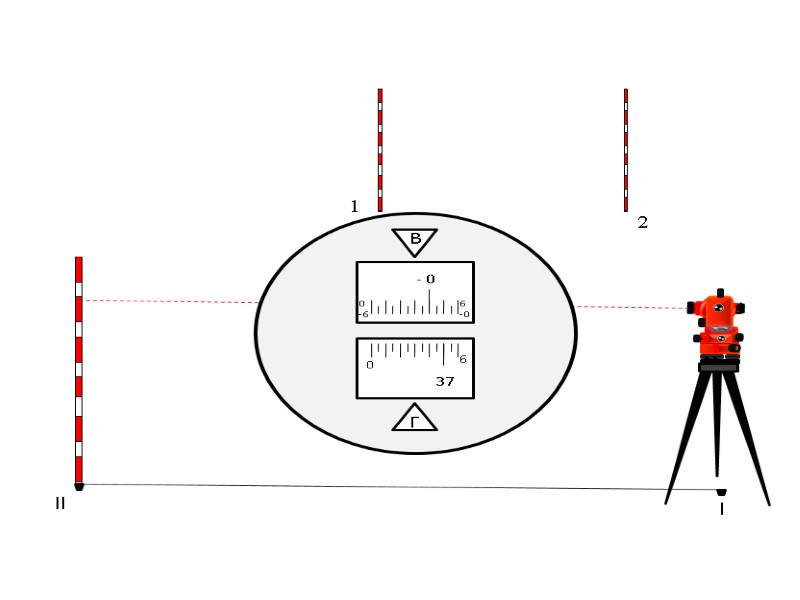
l ll 1 2
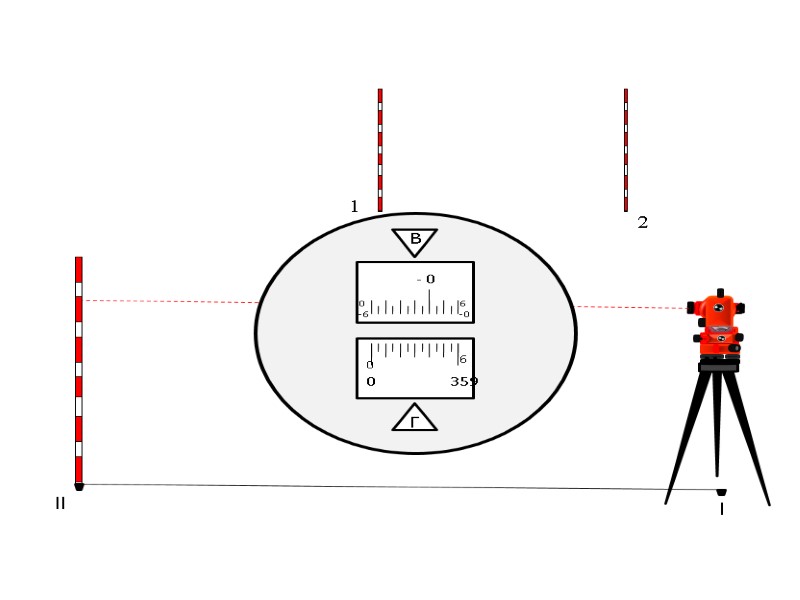
l ll 0 1 2
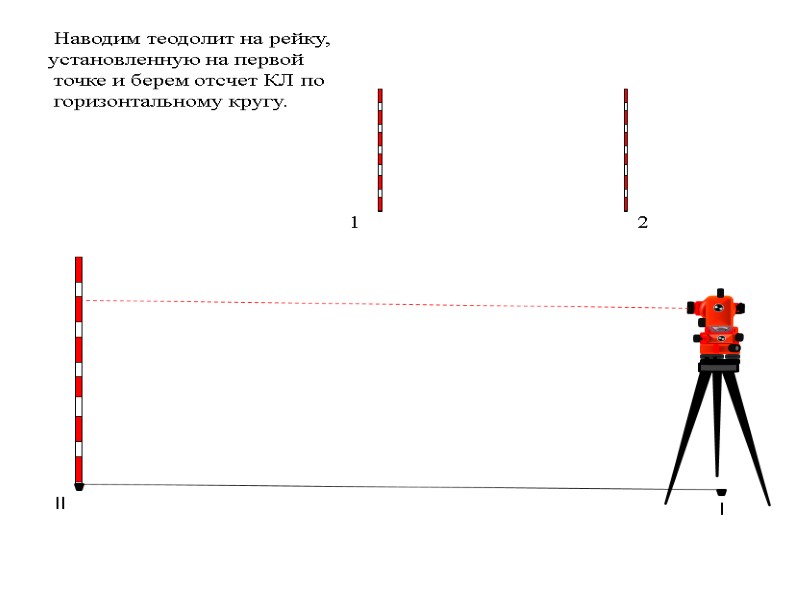
l ll Наводим теодолит на рейку, установленную на первой точке и берем отсчет КЛ по горизонтальному кругу. 1 2
l ll 1 2
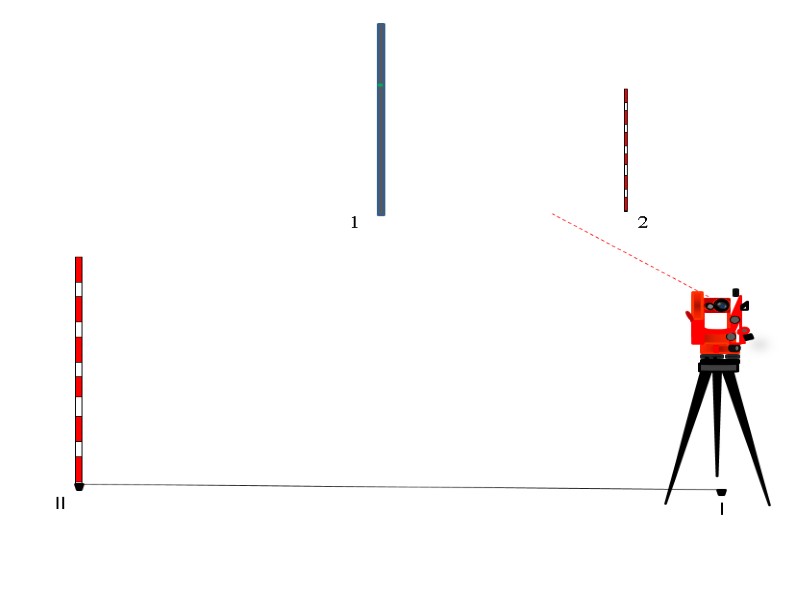
l ll 1 2
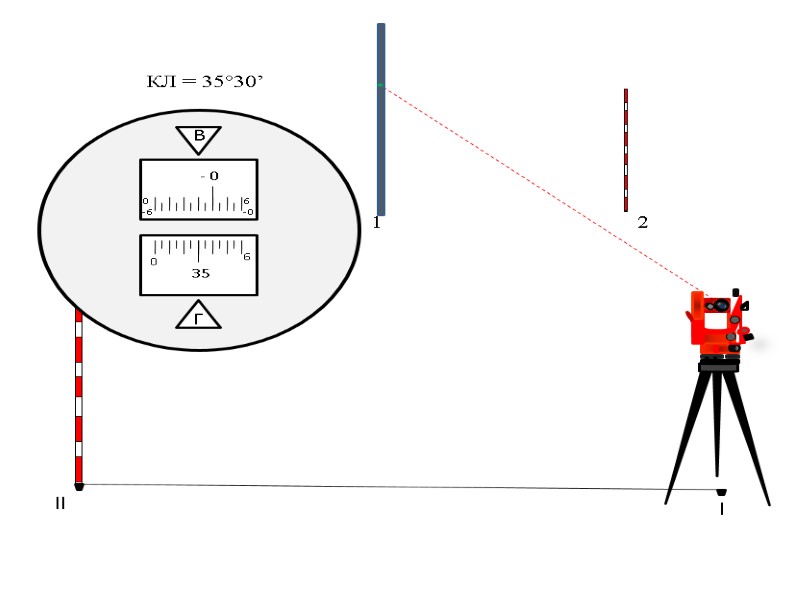
l ll КЛ = 35°30’ 1 2
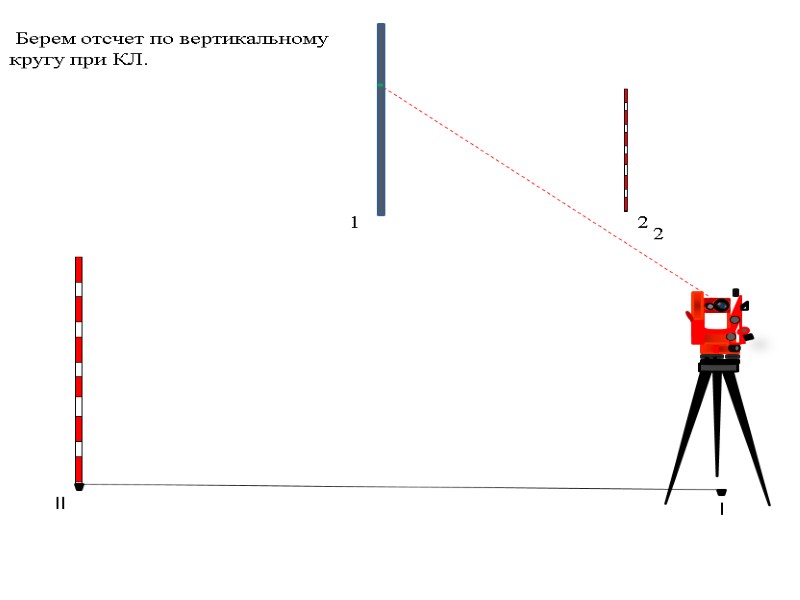
l ll Берем отсчет по вертикальному кругу при КЛ. 1 2 2
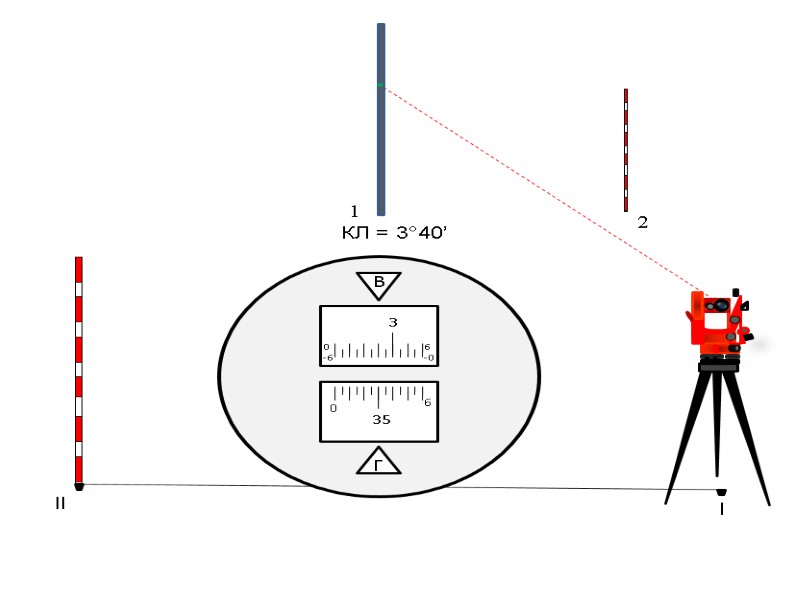
l ll КЛ = 3°40’ 1 2
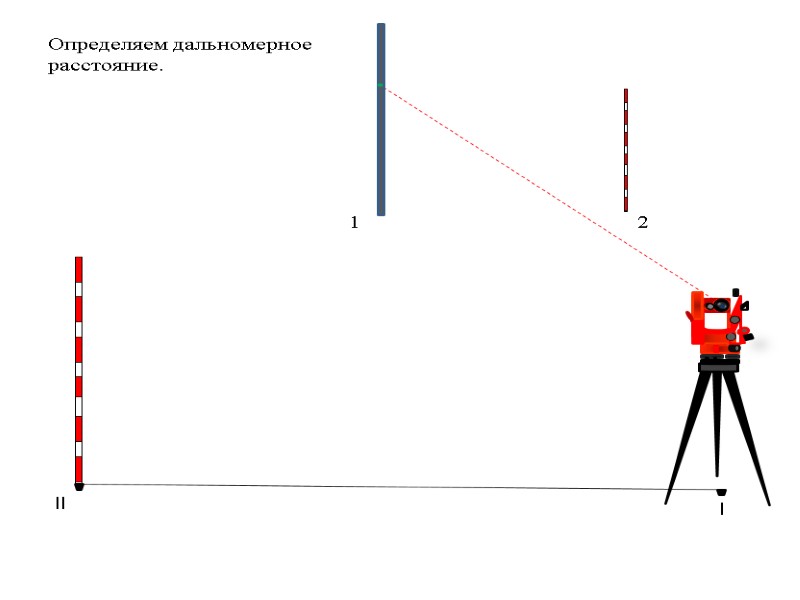
l ll Определяем дальномерное расстояние. 1 2
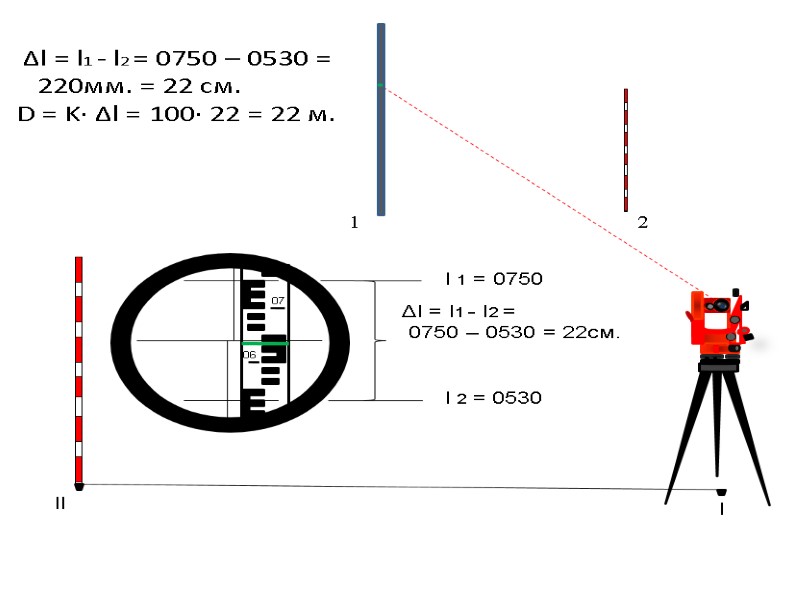
l ll Δl = l1 - l2 = 0750 – 0530 = 220мм. = 22 см. D = K· Δl = 100· 22 = 22 м. 1 2
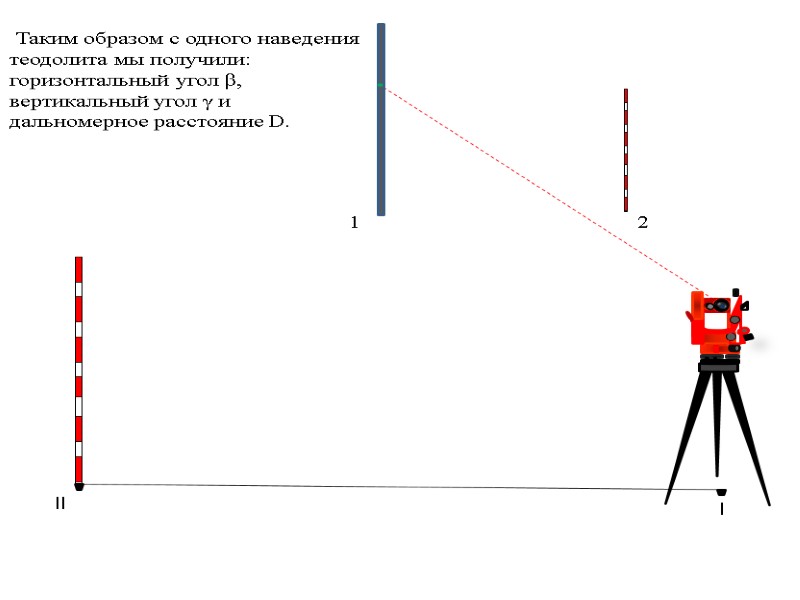
l ll Таким образом с одного наведения теодолита мы получили: горизонтальный угол β, вертикальный угол γ и дальномерное расстояние D. 1 2
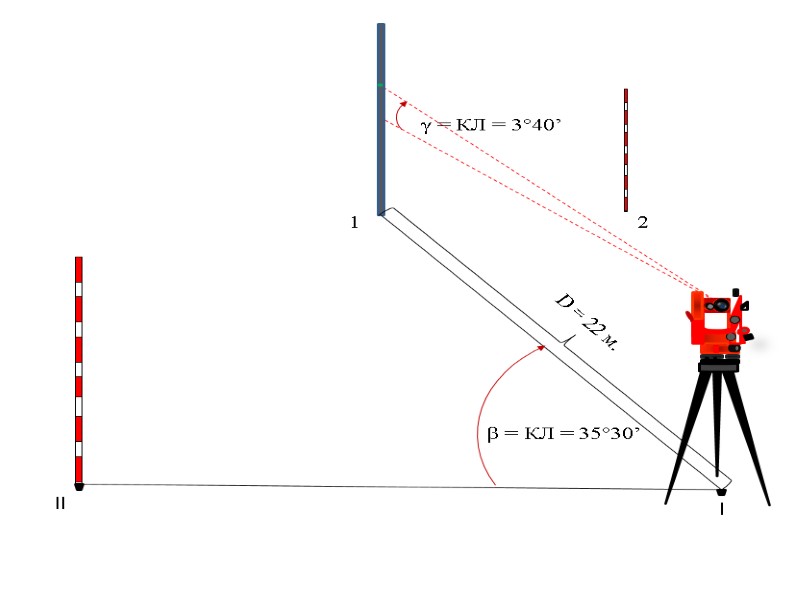
l ll β = КЛ = 35°30’ γ = КЛ = 3°40’ D = 22 м. 1 2

Горизонтальное проложение вычисляется по формуле: d = D · cosγ = 22 м. · cos 3°40’ = 21.95 м. Превышение h находим по формуле: h = d · tg γ = 21.95 · 0.064 = 1.405 м., так как ί = l, а D = 22 м. < 300 м. Абсолютную отметку точки 1 определяем по формуле: Нl = Hl + h = 100 + 1.405 = 101.405 м., где Нl = 100 м. абсолютная отметка станции № l, h - превышение т.1 над станцией № l. Аналогичным образом определяем положение точки 2. После определения всех точек со станции № l переносим теодолит на станцию № ll , замеряем высоту прибора, делаем отметку на рейке равную высоте прибора, устанавливаем рейку на станцию № l и определяем место нуля при двух положениях вертикального круга. Убедившись, что МО меньше или равно 1’, рукояткой лимба горизонтального круга выводим отсчет по горизонтальному кругу на ноль.
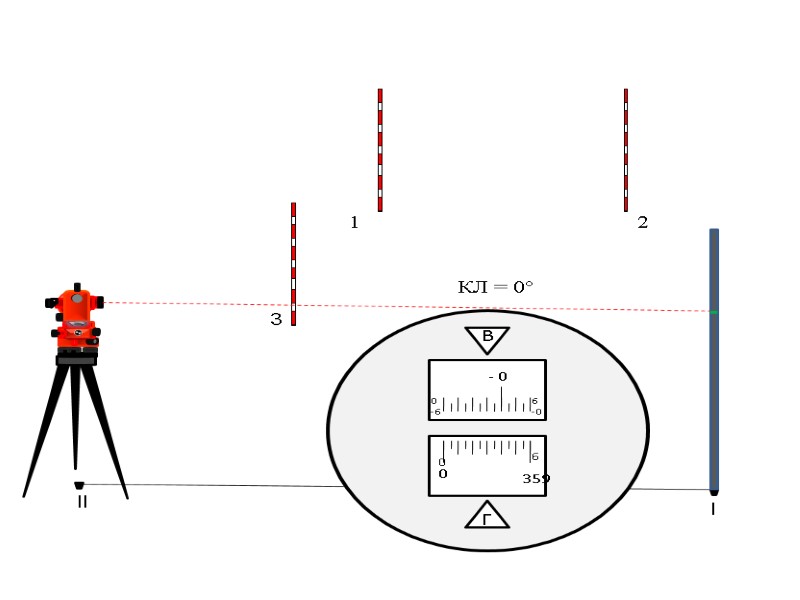
l 1 2 3 КЛ = 0° 0
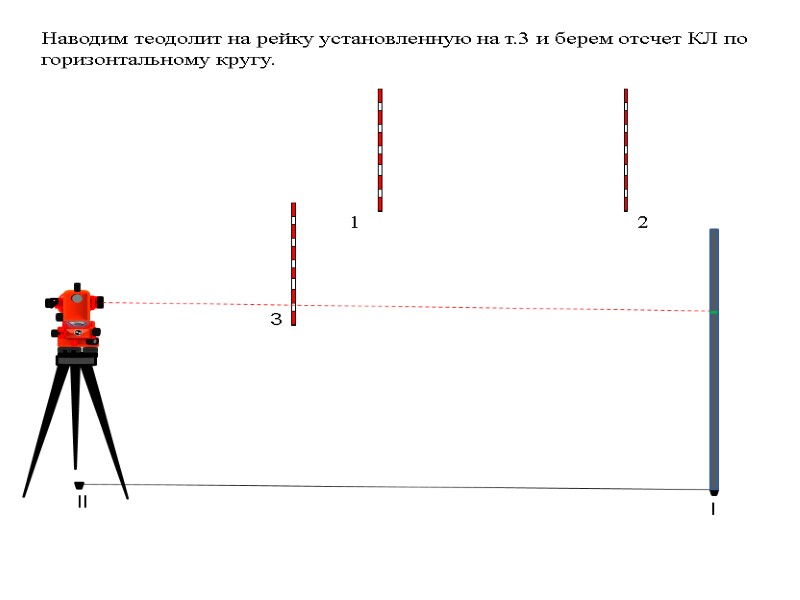
l 1 2 3 Наводим теодолит на рейку установленную на т.3 и берем отсчет КЛ по горизонтальному кругу.
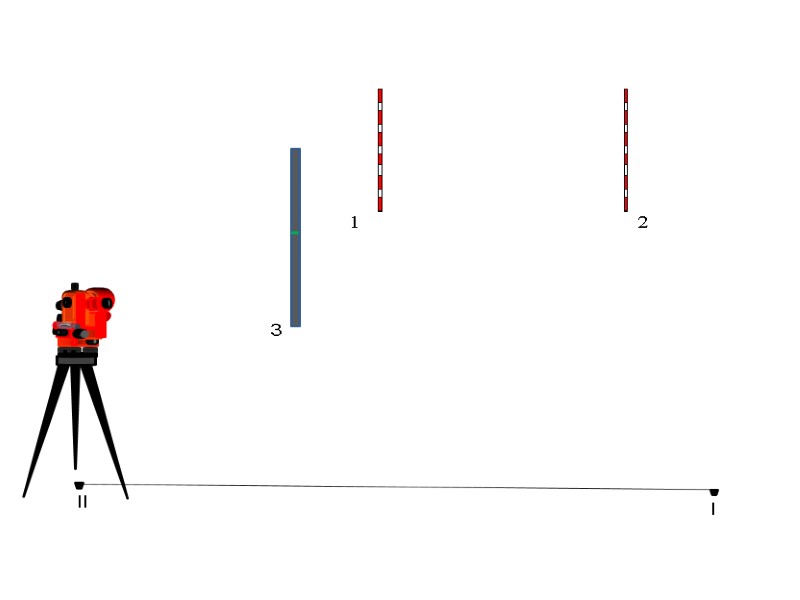
l 1 2 3
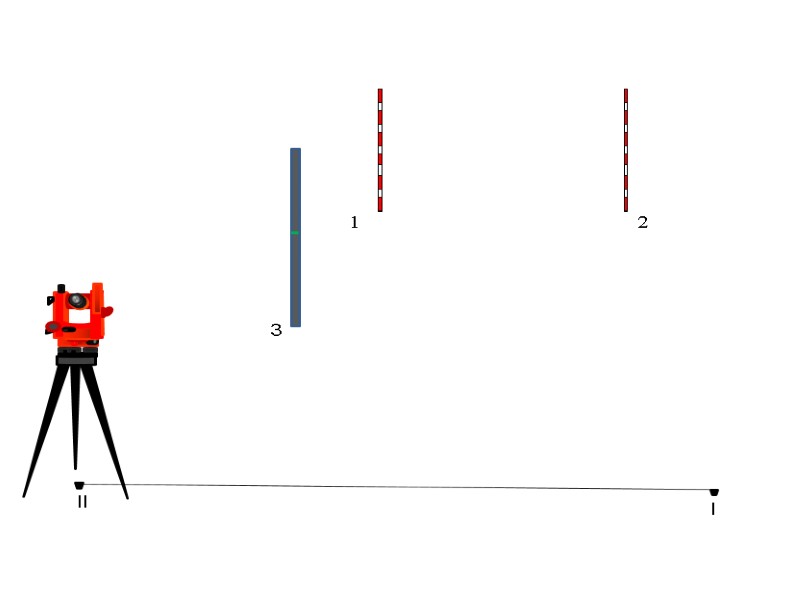
l 1 2 3
l 1 2 3
l 1 2 3
l 1 2 3
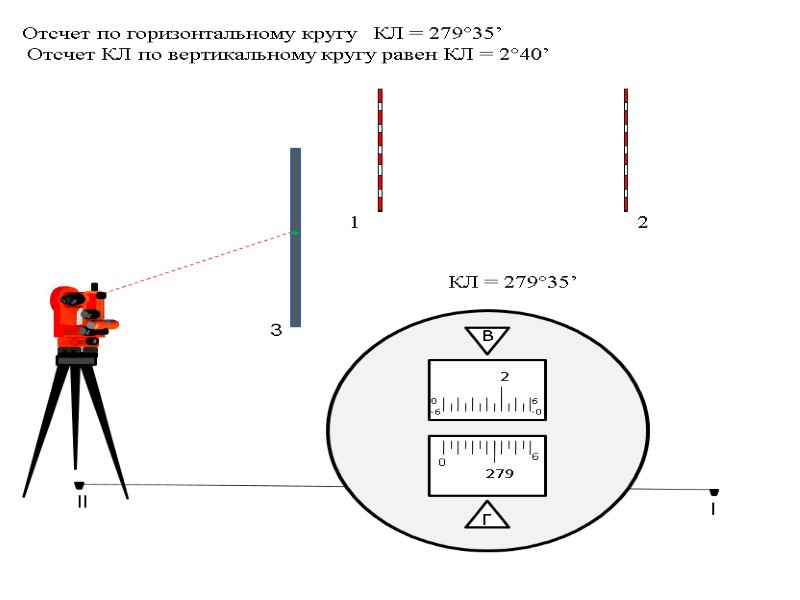
l 1 2 3 КЛ = 279°35’ Отсчет по горизонтальному кругу Отсчет КЛ по вертикальному кругу равен КЛ = 2°40’ КЛ = 279°35’
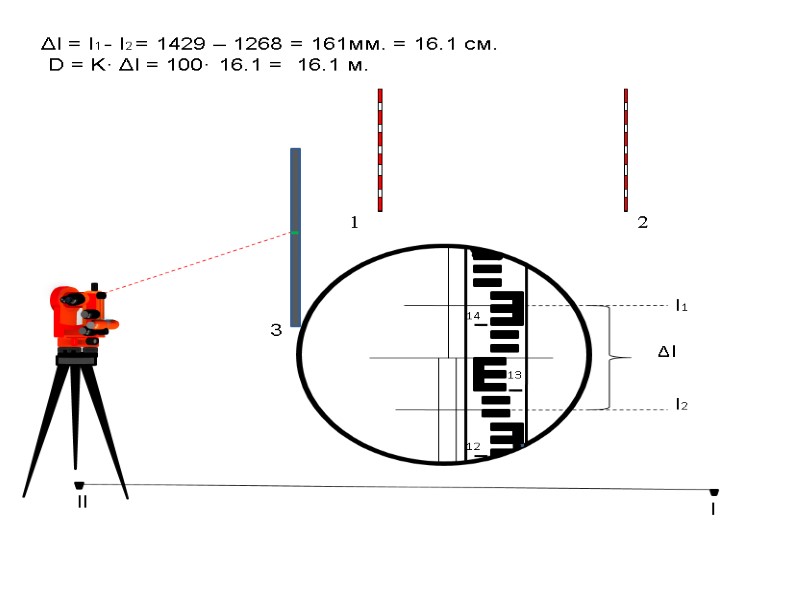
l 1 2 3 Δl = l1 - l2 = 1429 – 1268 = 161мм. = 16.1 см. D = K· Δl = 100· 16.1 = 16.1 м.
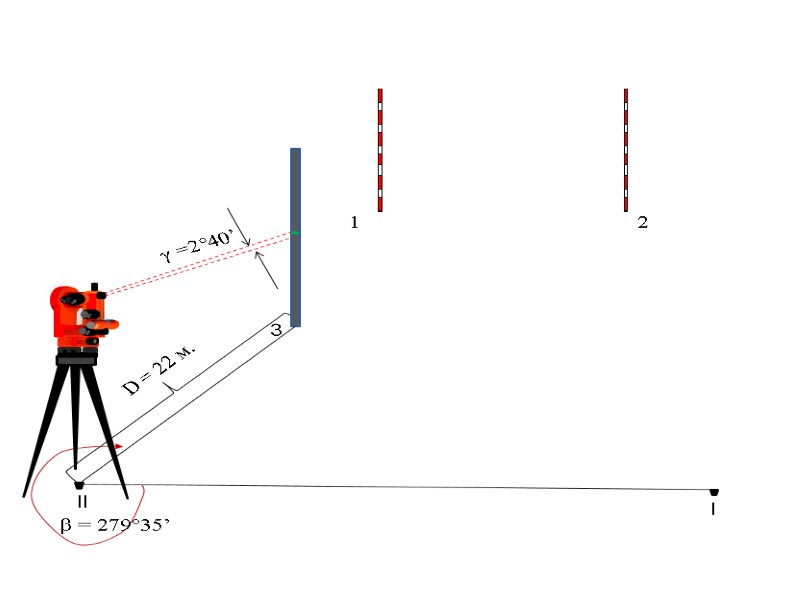
l 1 2 3 β = 279°35’ D = 22 м. γ =2°40’
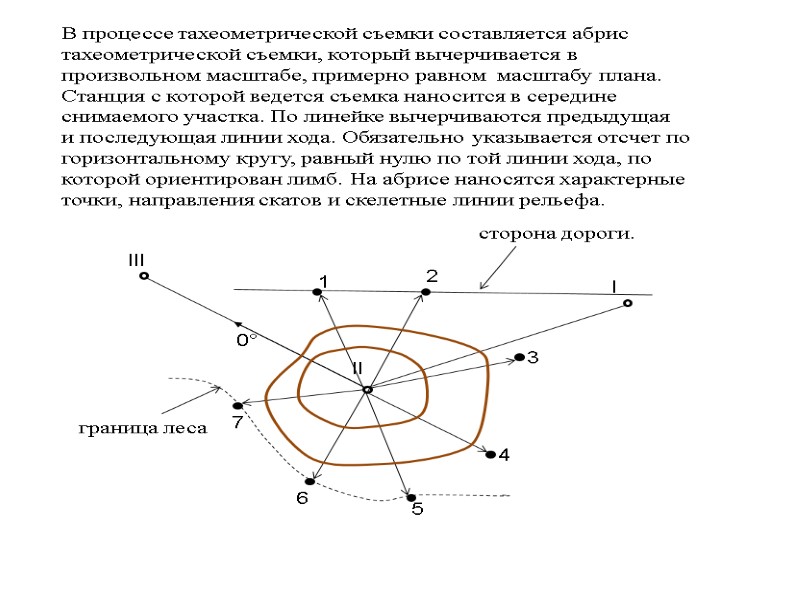
В процессе тахеометрической съемки составляется абрис тахеометрической съемки, который вычерчивается в произвольном масштабе, примерно равном масштабу плана. Станция с которой ведется съемка наносится в середине снимаемого участка. По линейке вычерчиваются предыдущая и последующая линии хода. Обязательно указывается отсчет по горизонтальному кругу, равный нулю по той линии хода, по которой ориентирован лимб. На абрисе наносятся характерные точки, направления скатов и скелетные линии рельефа. l ll lll 0° 1 3 2 7 5 6 4 граница леса сторона дороги.
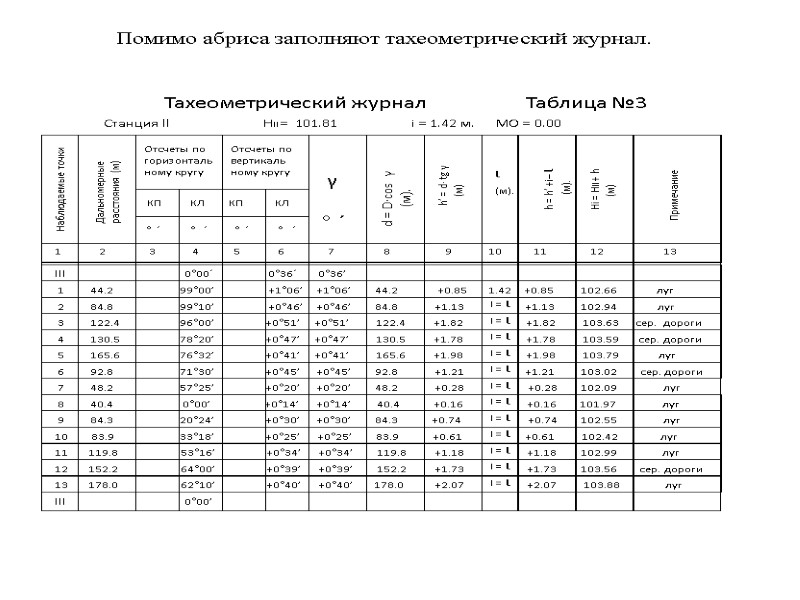
Помимо абриса заполняют тахеометрический журнал.

ВЫНЕСЕНИЕ НА ПЛАН РЕЕЧНЫХ ТОЧЕК . Реечные точки выносятся на план полярным способом (по горизонтальному углу и горизонтальному расстоянию), с помощью масштабной линейки, циркуля измерителя и транспортира. Все точки были сняты со станций ll и lll. 90° 0° 180° lll ll Отсчет по горизонтальному кругу со стации ll на станцию lll равен 0°00´. Горизонтальные углы откладываются по часовой стрелке. Например угол на т.1 равен 99°00´.
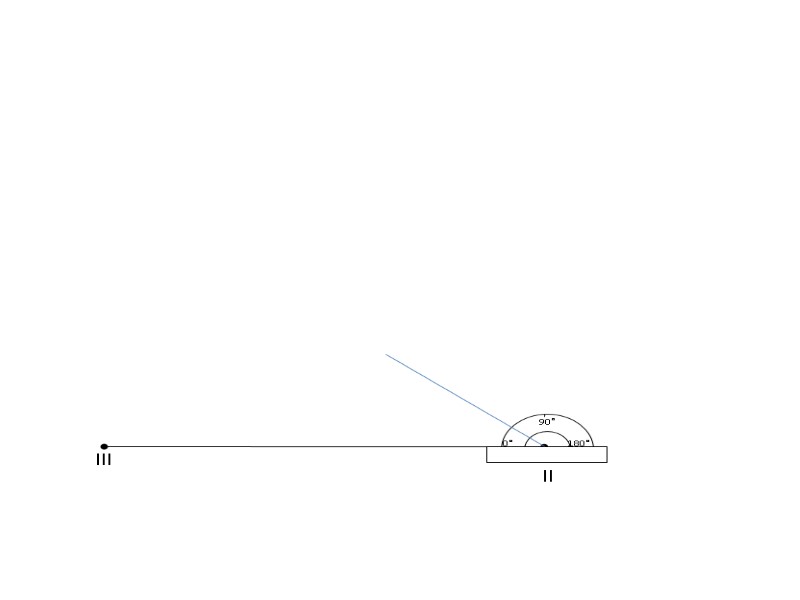
90° 0° 180° lll ll
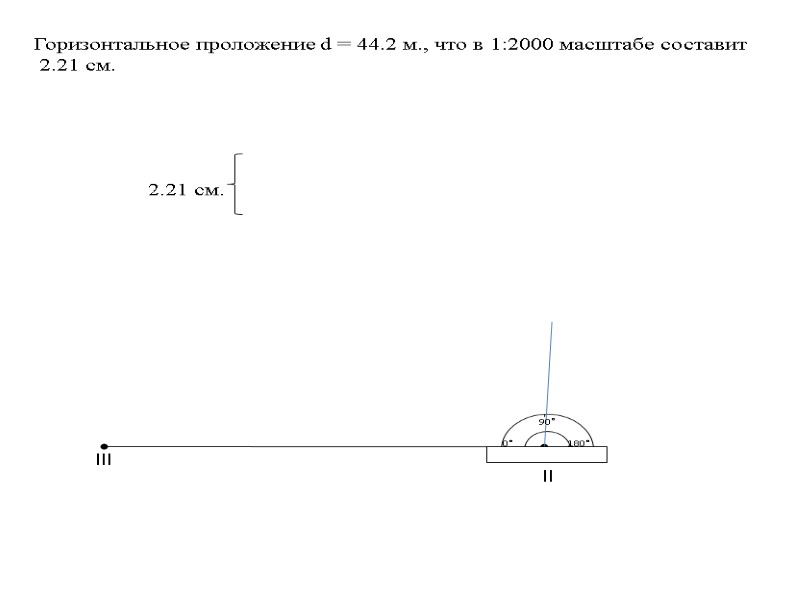
90° 0° 180° lll ll Горизонтальное проложение d = 44.2 м., что в 1:2000 масштабе составит 2.21 см. 2.21 см.
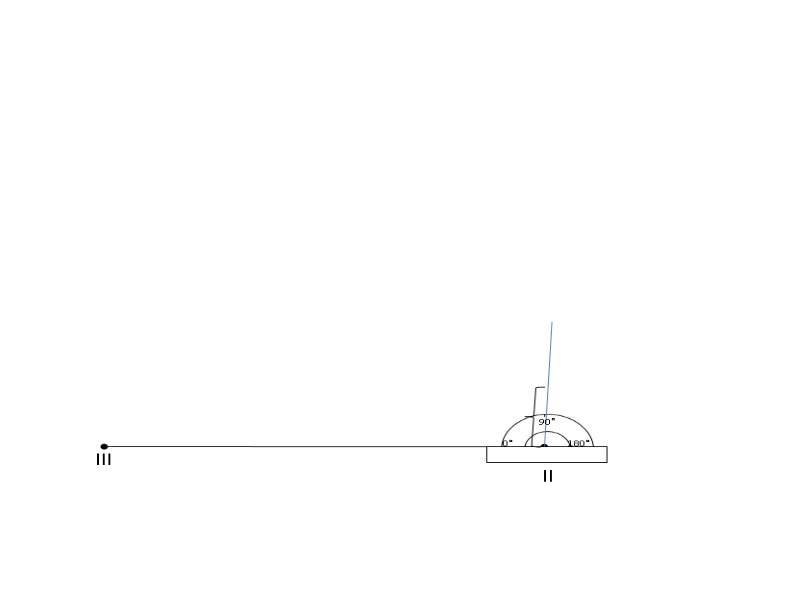
90° 0° 180° lll ll
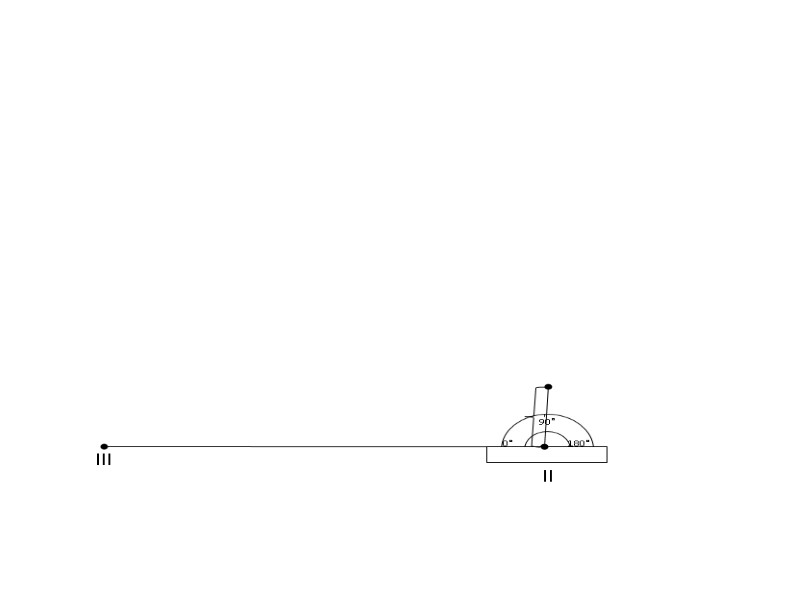
90° 0° 180° lll ll
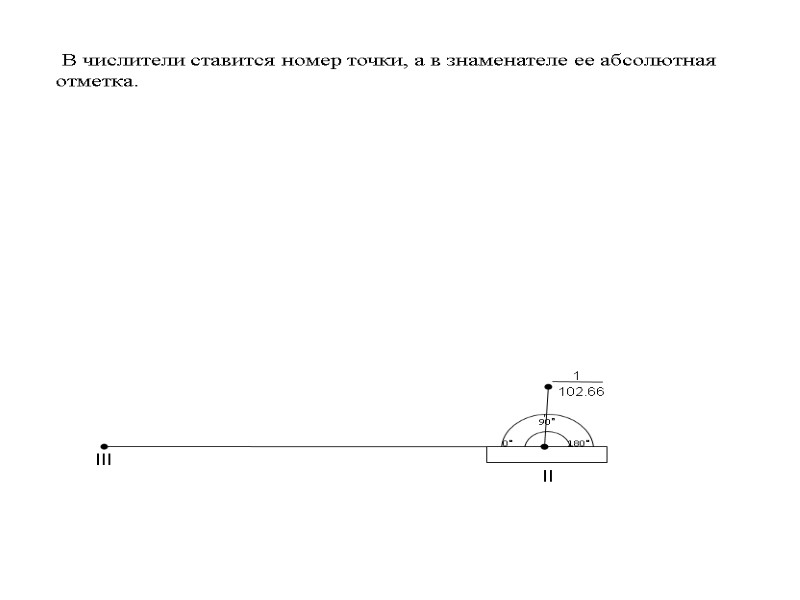
90° 0° 180° lll ll 1 102.66 В числители ставится номер точки, а в знаменателе ее абсолютная отметка.
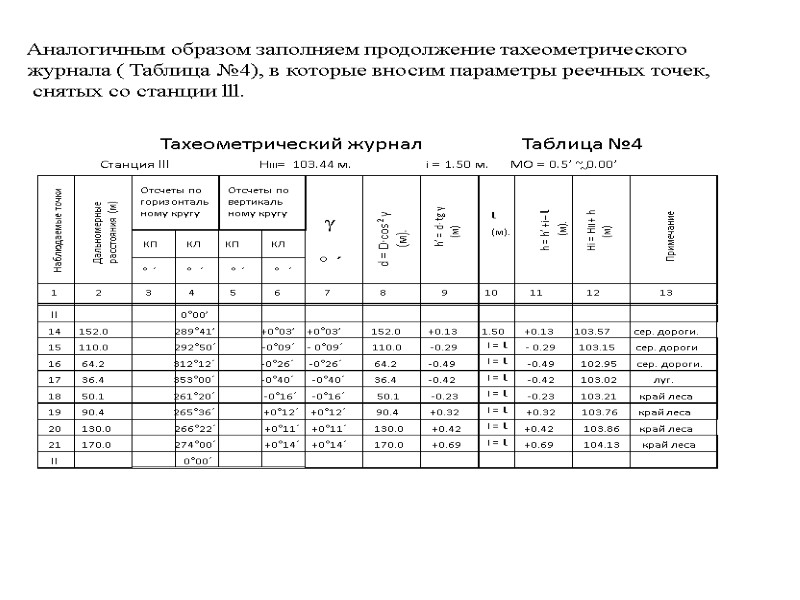
Аналогичным образом заполняем продолжение тахеометрического журнала ( Таблица №4), в которые вносим параметры реечных точек, снятых со станции lll.

lll ll 1 102.66 Отсчет по горизонтальному кругу со станции lll на станцию ll, также равен 0°00´. Для примера возьмем точку 14. Откладываем углы по часовой стрелке. 0° 90° 180°
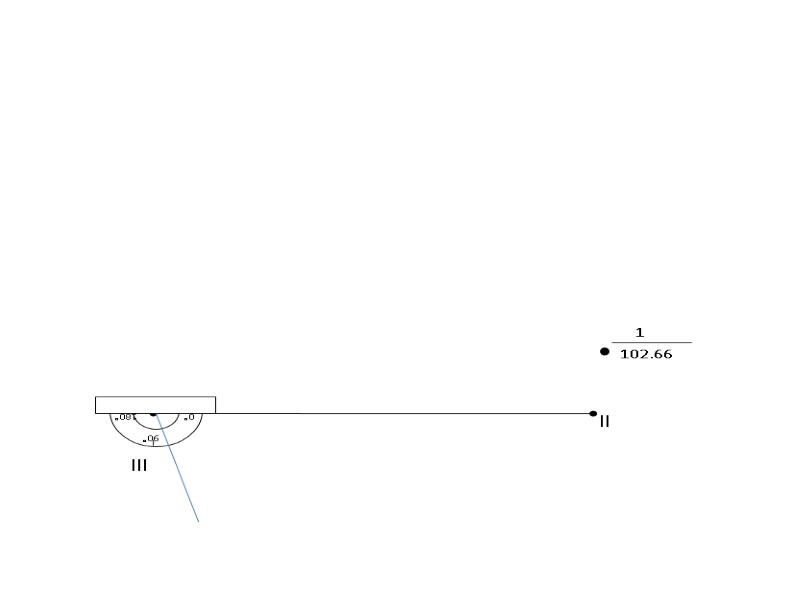
lll ll 1 102.66 0° 90° 180°
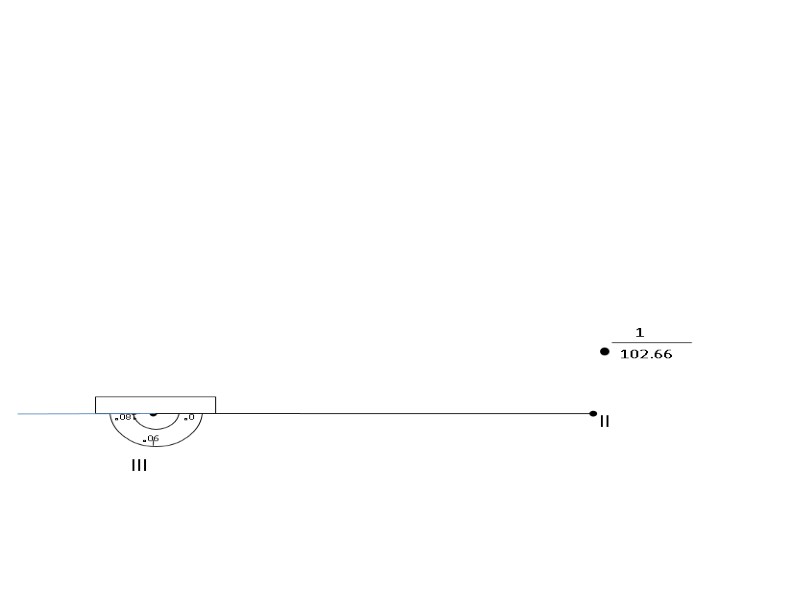
lll ll 1 102.66 0° 90° 180°
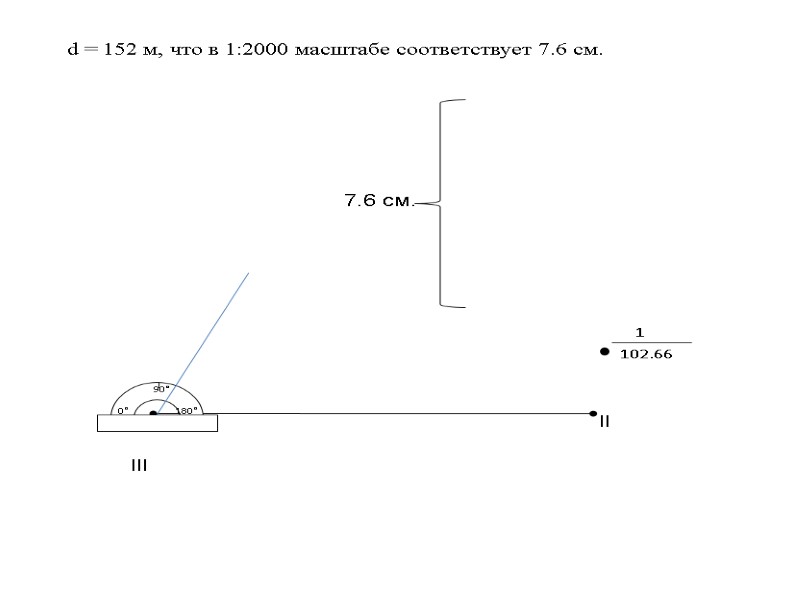
lll ll 1 102.66 d = 152 м, что в 1:2000 масштабе соответствует 7.6 см. 7.6 см.
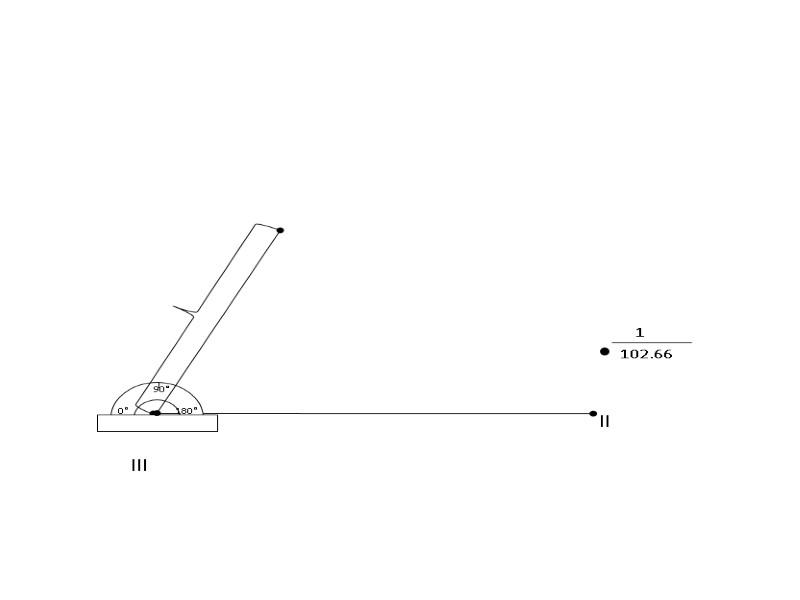
lll ll 1 102.66
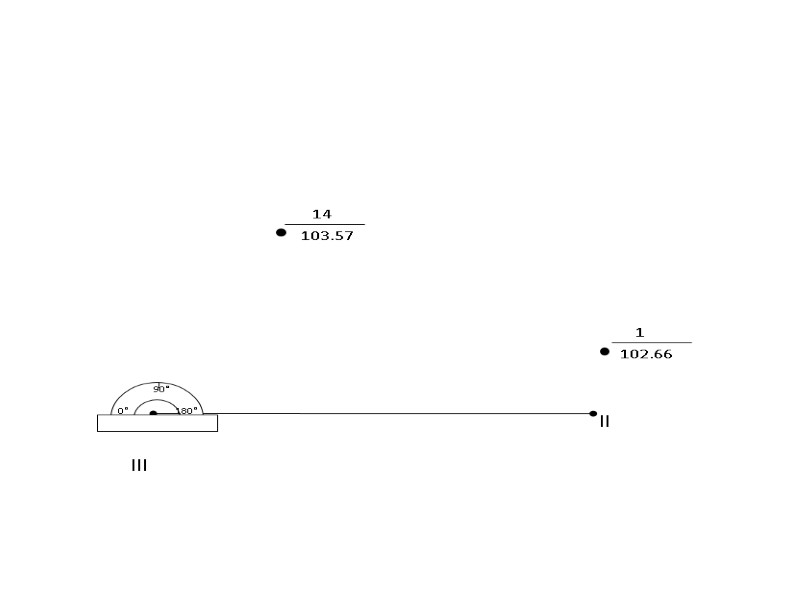
lll ll 1 102.66 14 103.57


ЭЛЕКТРОННЫЙ ТАХЕОМЕТР 3ТА5Р Электронный тахеометр 3Та5Р предназначен для выполнения крупномасштабных топографических съемок, создания сетей планово-высотного обоснования, решения геодезических и инженерных задач на местности. Тахеометром можно производить измерение горизонтальных и вертикальных углов, получать результаты измерений в виде горизонтальных проложений и превышений, выполнять измерение полярных координат, а также получать вычисленные прямоугольные координаты.




Закрепительный винт вертикаль -ного круга. Наводящий винт вертикаль- ного круга. Паз для установки кассетного источника питания.




Электронный тахеометр TOPCON GTS-102N Тахеометр GTS-102N производит любые угломерные измерения одновременно с измерением расстояний и по полученным данным проводит инженерные вычисления, сохраняя всю полученную информацию. С помощью электронного тахеометра в полевых условиях можно получить информацию об измеряемых горизонтальных и вертикальных углах и расстояниях, автоматически выполнить необходимые вычисления по плановому и высотному положению ситуации. При наличии компьютера процесс может быть автоматизирован, включая получение готовой карты местности за считанные минуты. Возможность занесения в запоминающее устройство допустимых погрешностей измерений позволяет повысить точность и производительность измерений.













Измерение углов. Измерение вертикального и правого горизонтального угла. Перед началом измерения углов зрительная труба наводится на светлый предмет. Вращая кольцо окуляра, добиваемся четкого изображения сетки нитей. По визиру зрительная труба наводится на цель. При помощи кремальеры добиваемся четкости изображения выбранной цели. Если при наблюдении в зрительную трубу, видим что между сеткой нити и выбранной целью возникает параллакс, то он устраняется тщательной фокусировкой сетки нити и цели. Порядок измерения вертикального и правого горизонтального углов показан ниже.

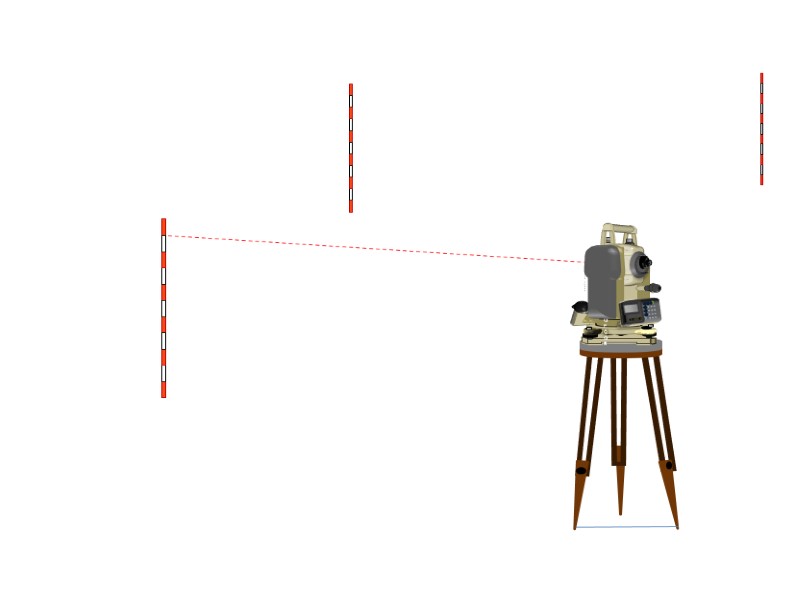



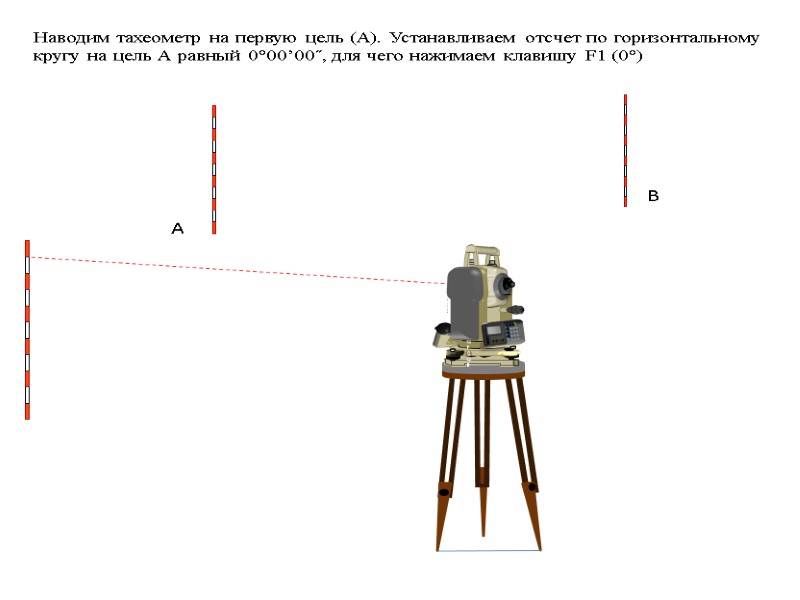


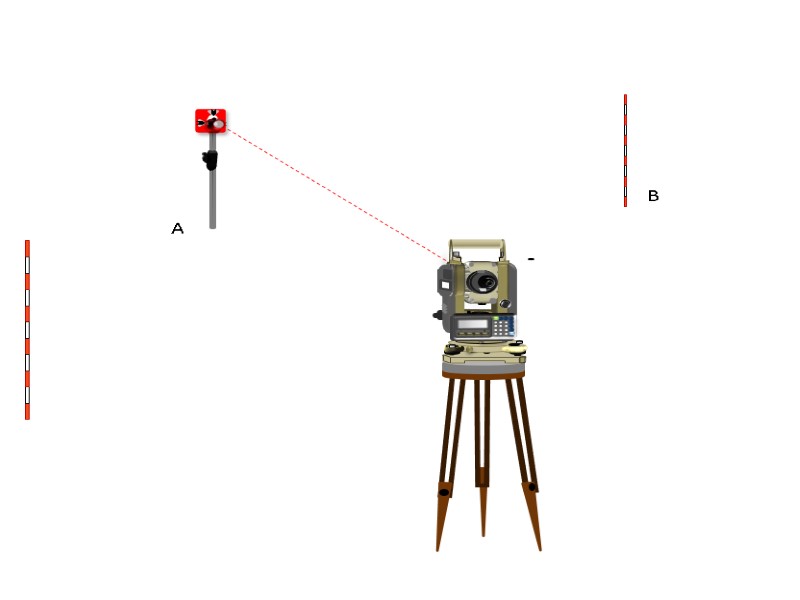



Установка ГК=0° OK? … … [Да] [Нет] Нажать клавишу F3 [ДА]

Установка ГК=0° OK? … … [Да] [Нет]



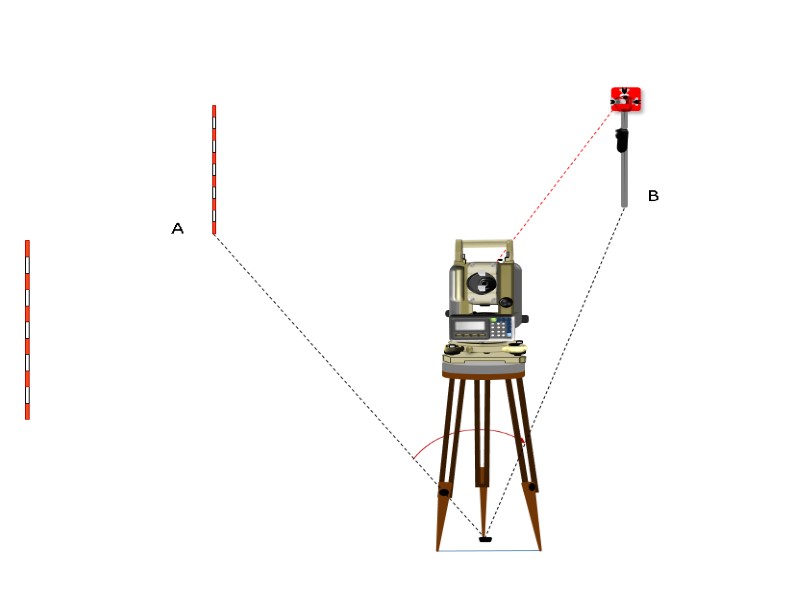



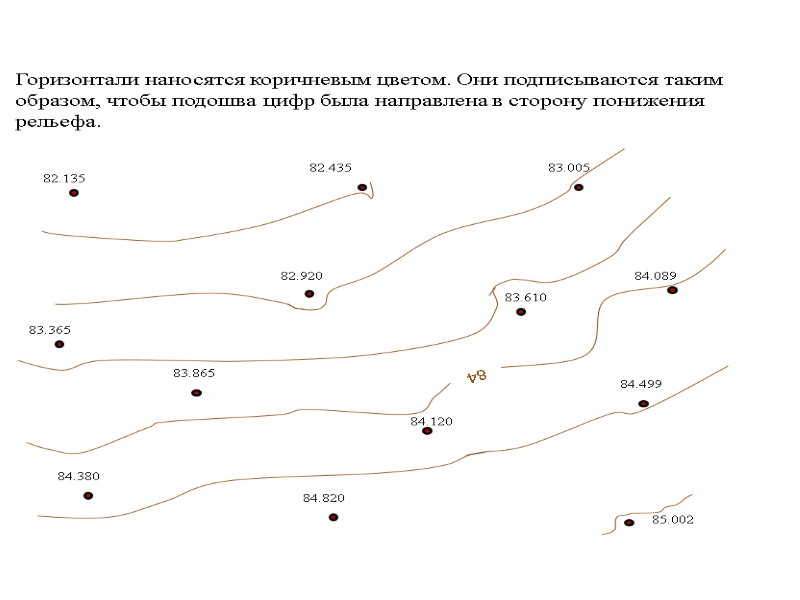
РЕЛЬЕФ МЕСТНОСТИ И ЕГО ИЗОБРАЖЕНИЕ. Под рельефом местности подразумевается совокупность неровностей земной поверхности . Рельеф местности – важнейший элемент содержания топографических карт. Учету рельефа при всех видах строительства придается первостепенное значение. На современных картах рельеф изображается горизонталями. Горизонталь это замкнутая кривая соединяющая точки с одинаковыми высотными отметками и имеющая следующие свойства: а) горизонтали замкнутые кривые, б) горизонтали не пересекаются, в) чем меньше расстояние между горизонталями на карте, тем круче скат на местности. Расстояние между горизонталями по отвесной линии называется высотой сечения рельефа, она подписывается на картах под линейным масштабом. Расстояние между горизонталями в плане называется заложением. В зависимости от масштаба карты и характера рельефа высоты сечения могут быть равны 1; 2; 5 и 10 м. При слабовыраженном рельефе или более точном его изображении горизонтали могут проводиться через 0.25 и 0.5 м.. Горизонталь представляет собой линию, полученную при пересечении поверхности земли плоскостью параллельной ее уровенной поверхности.


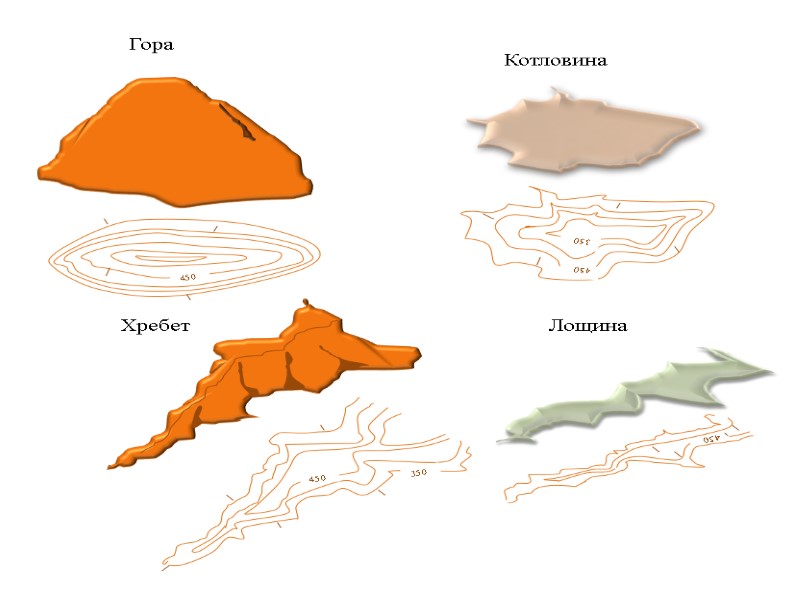
Из многочисленных форм рельефа можно выделить следующие: 1.Гора, холм, сопка-основание горы подошва, наивысшая точка вершина, вершина в виде площадки плато. 2. Котловина, впадина- чашеобразные замкнутые со всех сторон углубления, нижняя часть дно, верхний край бровка. 3. Хребет - вытянутая возвышенность, понижающаяся в одном направлении , имеющая два крутых склона, пересечение которых образуют ось называемую водораздельной линией. 4. Лощина – вытянутое углубление местности понижающееся в одном направлении. Нижняя часть лощины образует водослив или тальвег. 5. Седловина – пониженная часть местности между двумя соседними возвышенностями. Для выделения различных форм рельефа, изображенного горизонталями, направления скатов обозначают черточками (бергштрихами), а также надписями ( численные значения), где основание цифр направлено в сторону понижения местности. Мерой крутизны ската линии , служит ее уклон i, который определяется тангенсом угла наклона.
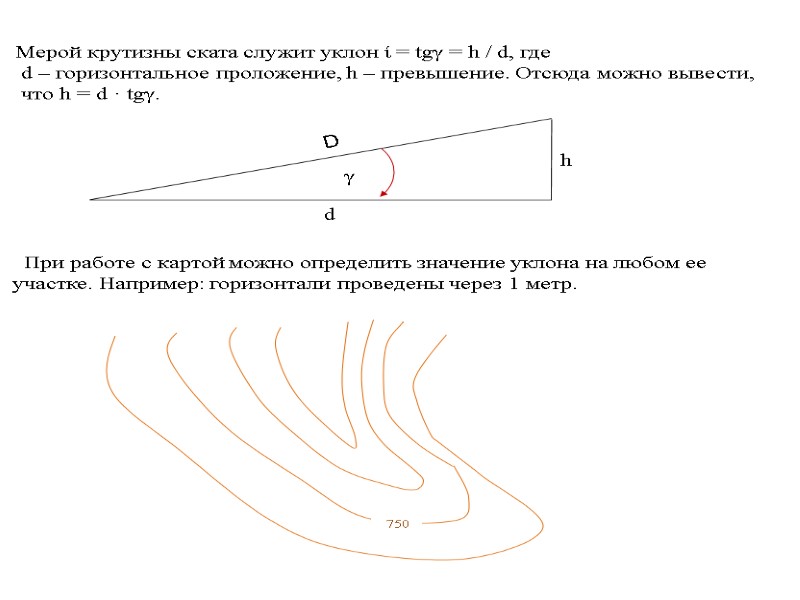


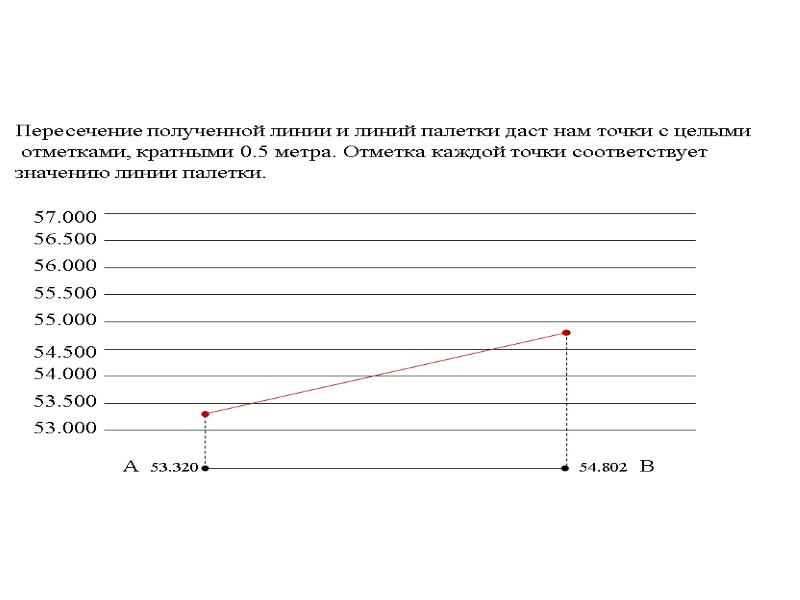
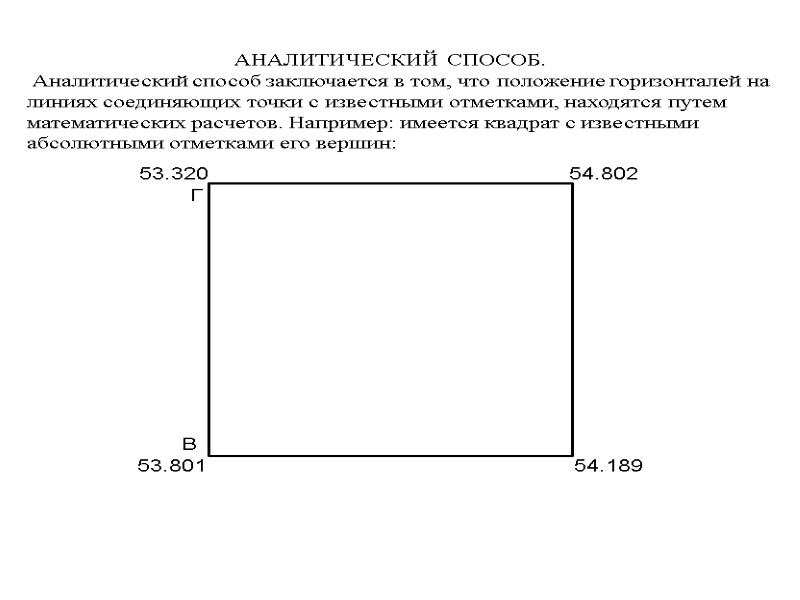
ПОСТРОЕНИЕ ГОРИЗОНТАЛЕЙ. Существует два способа построения горизонталей графический и аналитический. Графический способ. При графическом способе строится палетка, т. е. проводится ряд параллельных линий через 1 или 0.5 см. Например: требуется провести горизонтали через 0.5 метра между точками А с отметкой (53.320 м) и В с отметкой (54.802).








82.135 84.089 83.610 82.920 85.002 83.005 82.435 83.365 84.509 84.120 83.865 84.380 84.820 На листе прозрачной бумаги строим палетку.

82.135 84.089 83.610 82.920 85.002 83.005 82.435 83.365 84.509 84.120 83.865 84.380 84.820 Оцифровываем ее.
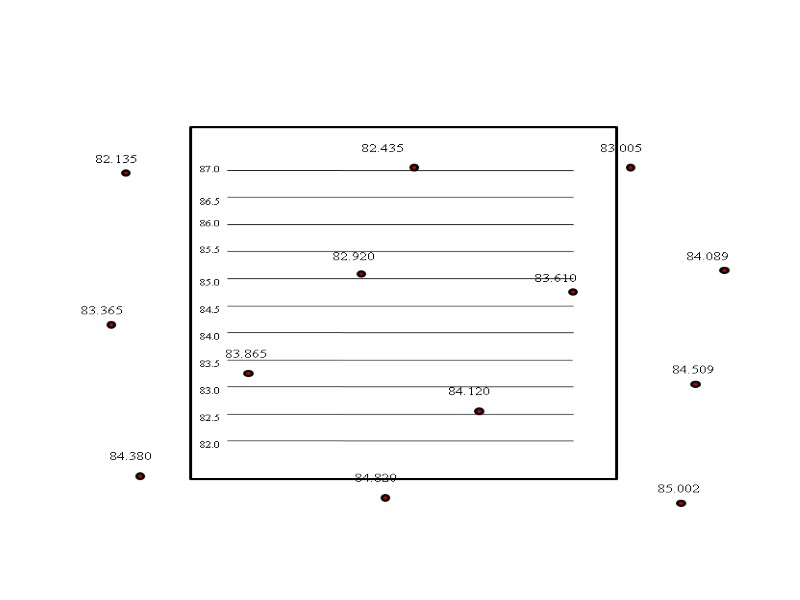
82.135 84.089 83.610 82.920 85.002 83.005 82.435 83.365 84.509 84.120 83.865 84.380 84.820
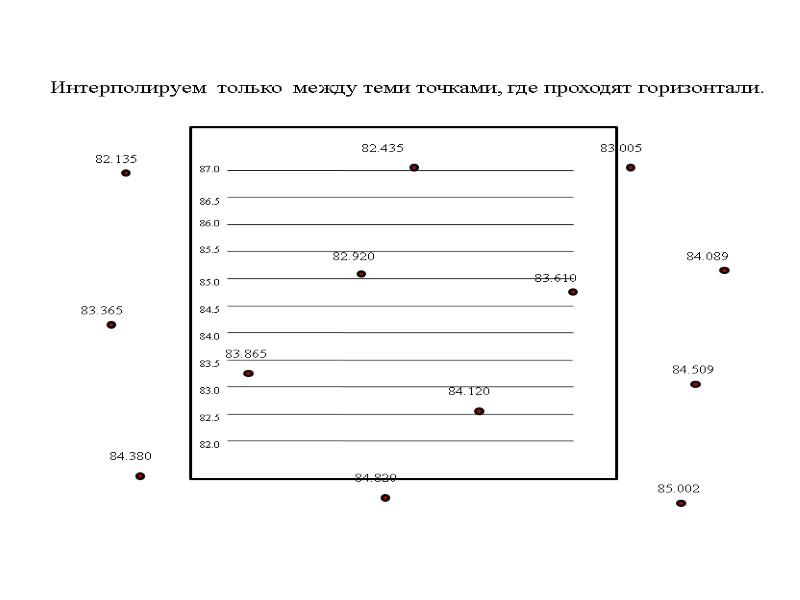
82.135 84.089 83.610 82.920 85.002 83.005 82.435 83.365 84.509 84.120 83.865 84.380 84.820 Интерполируем только между теми точками, где проходят горизонтали.

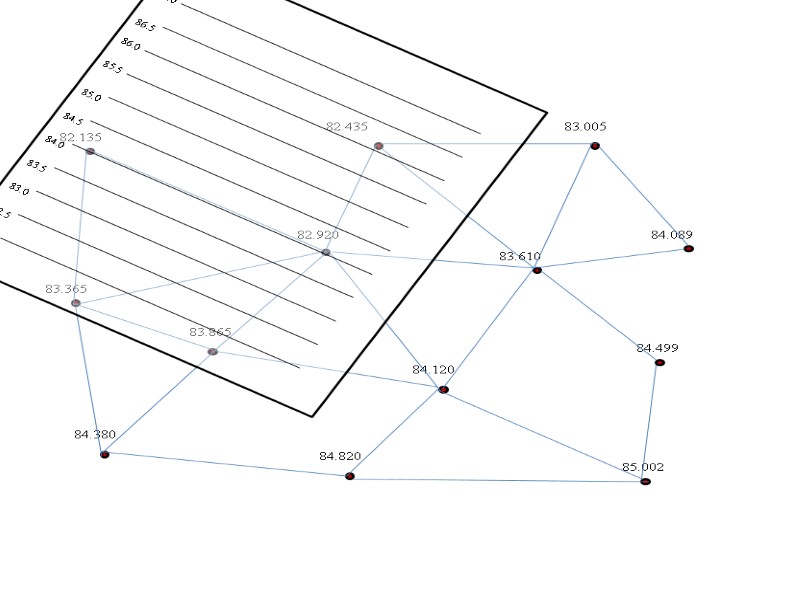
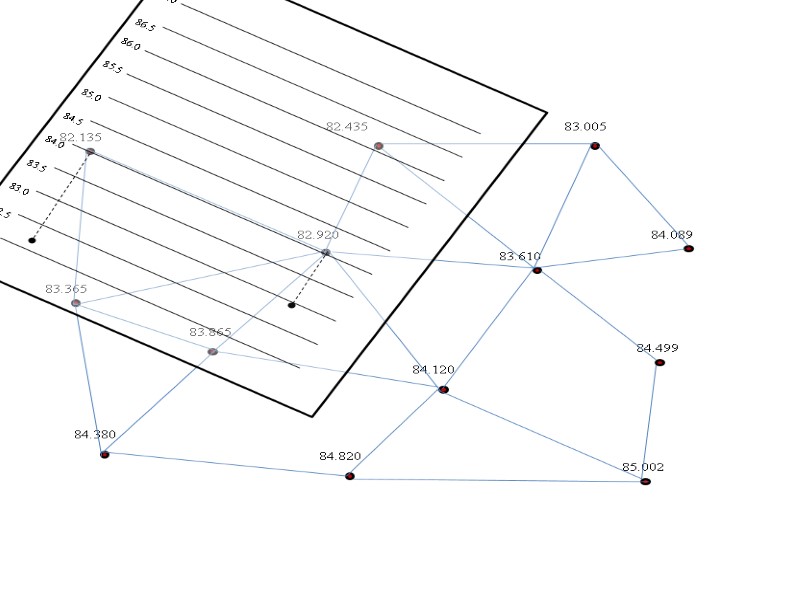


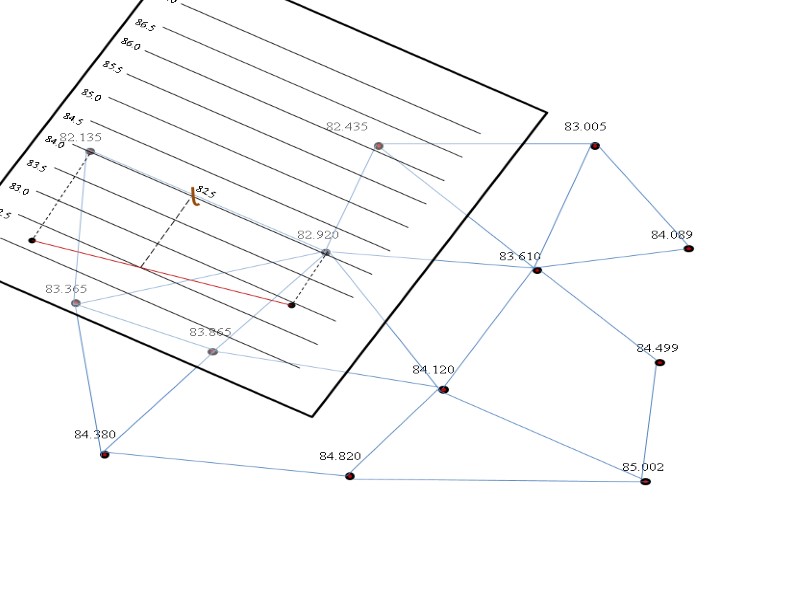
82.0 83.5 83.0 82.5 86.0 85.5 85.0 84.5 84.0 87.0 86.5 82.5
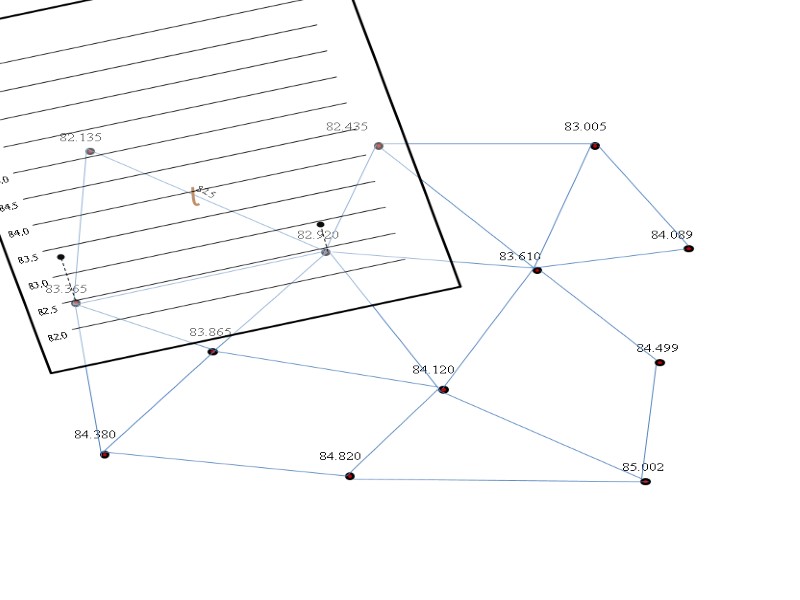
82.5
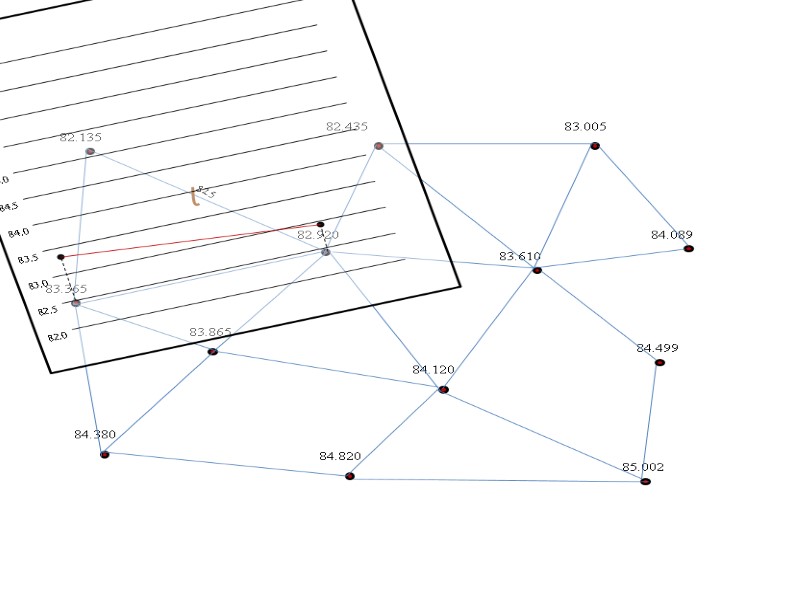
82.5
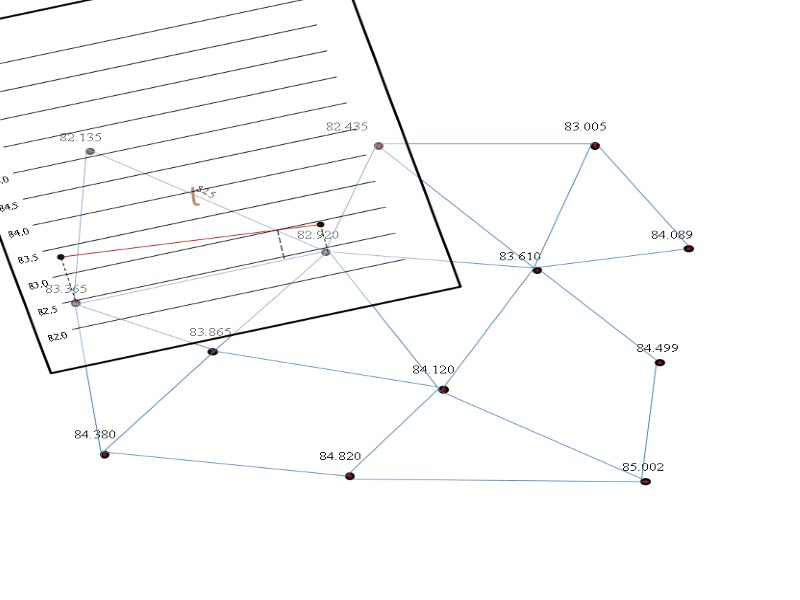
82.5
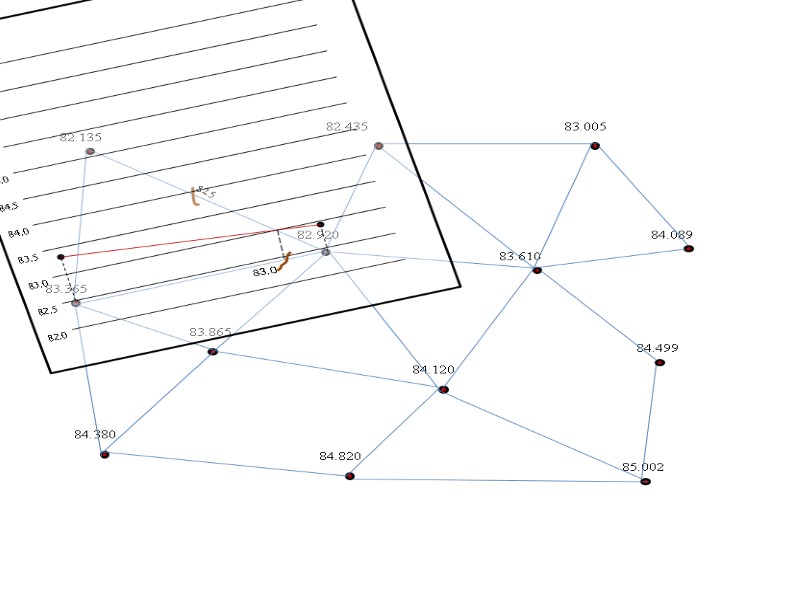
82.5 83.0
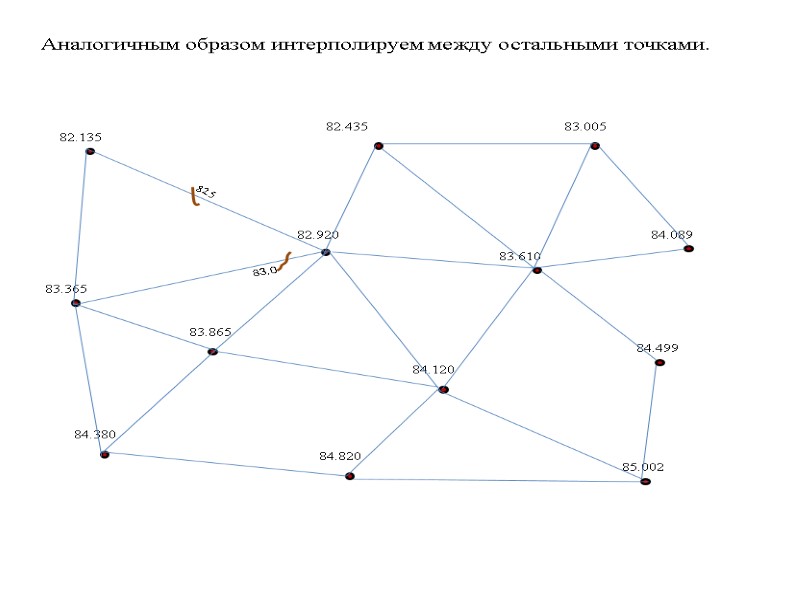
82.5 83.0 Аналогичным образом интерполируем между остальными точками.







54.5
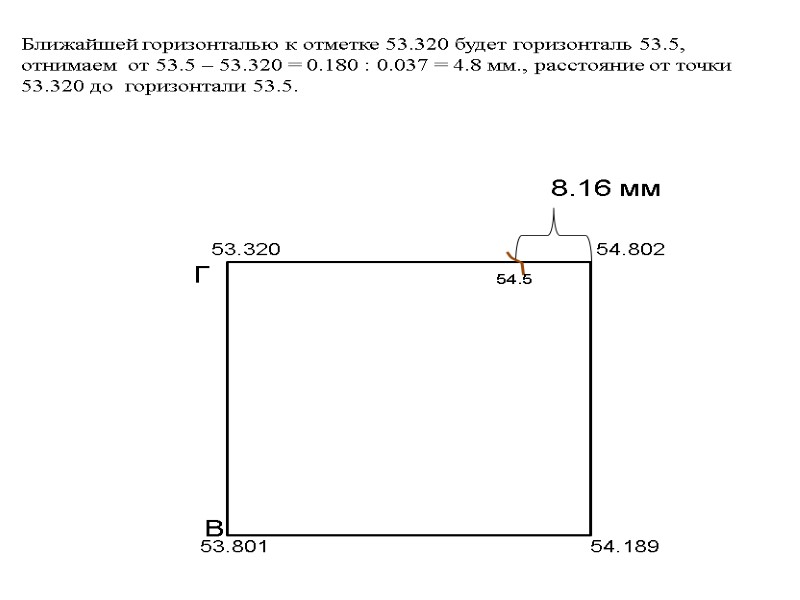
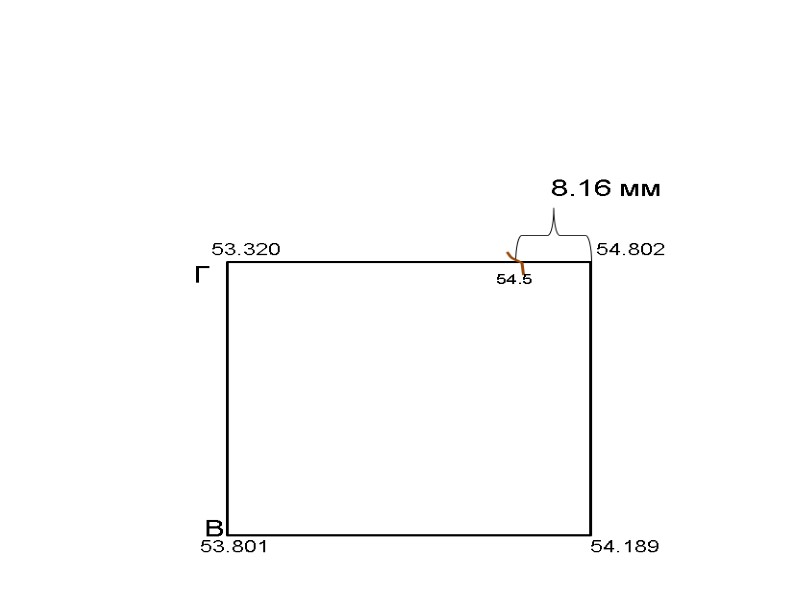
54.5 Ближайшей горизонталью к отметке 53.320 будет горизонталь 53.5, отнимаем от 53.5 – 53.320 = 0.180 : 0.037 = 4.8 мм., расстояние от точки 53.320 до горизонтали 53.5.
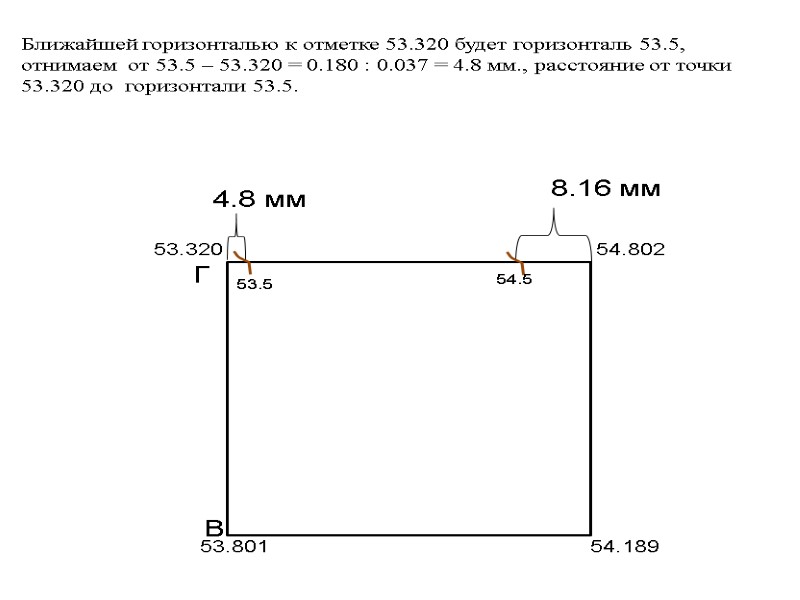
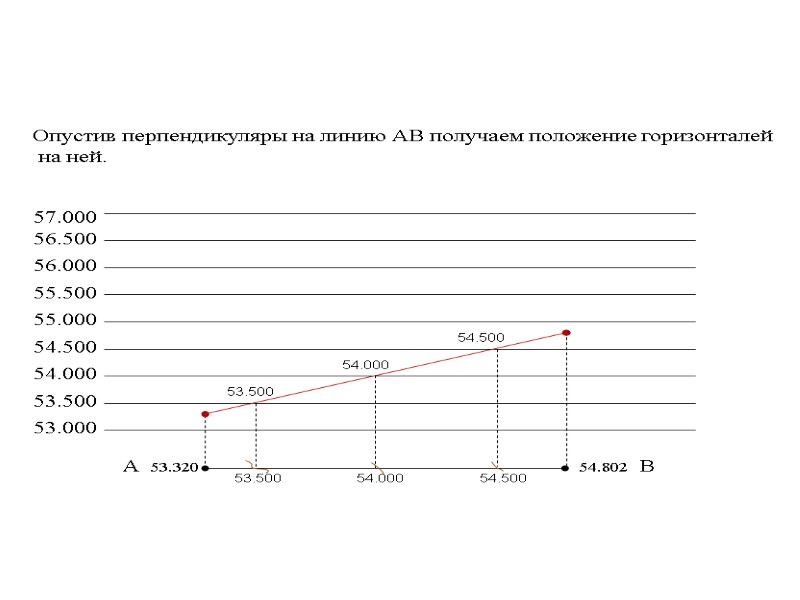
53.320 54.802 53.801 54.189 Г В 8.16 мм 54.5 Ближайшей горизонталью к отметке 53.320 будет горизонталь 53.5, отнимаем от 53.5 – 53.320 = 0.180 : 0.037 = 4.8 мм., расстояние от точки 53.320 до горизонтали 53.5. 53.5 4.8 мм
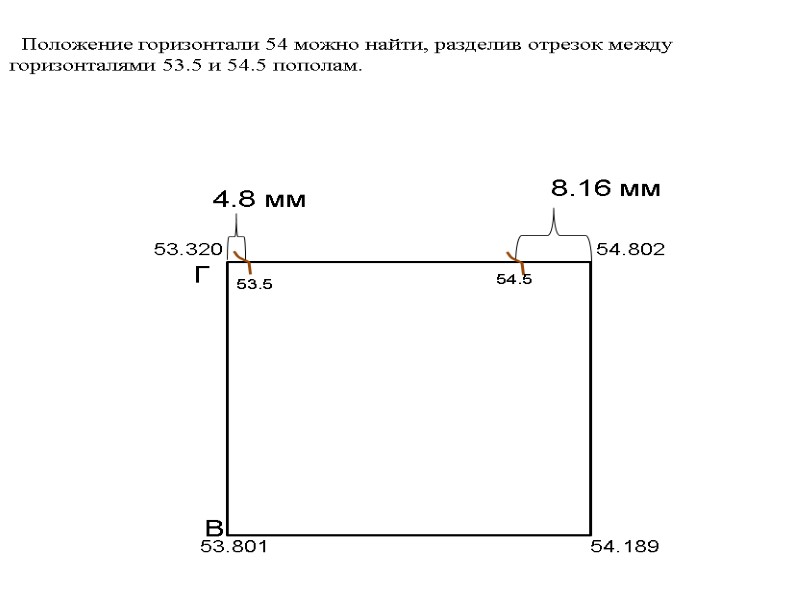
53.320 54.802 53.801 54.189 Г В 8.16 мм 54.5 53.5 Положение горизонтали 54 можно найти, разделив отрезок между горизонталями 53.5 и 54.5 пополам. 4.8 мм
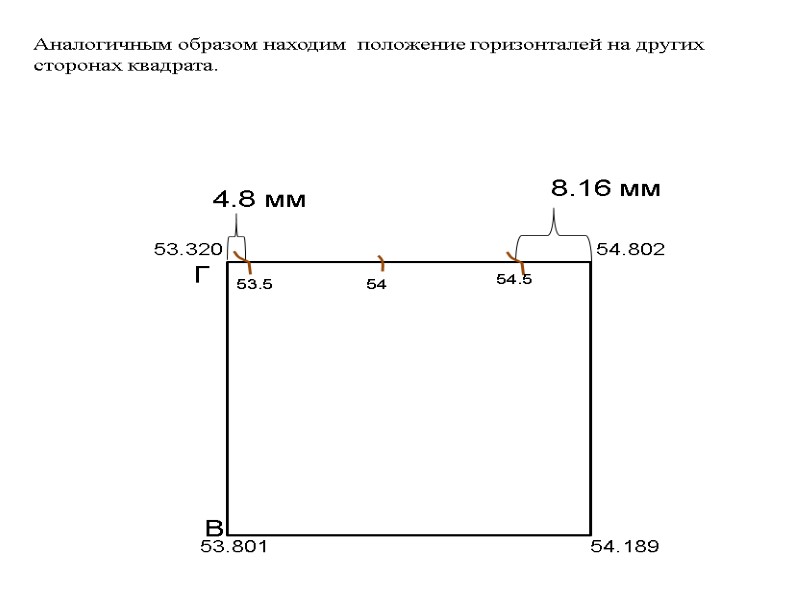
53.320 54.802 53.801 54.189 Г В 8.16 мм 54.5 53.5 54 Аналогичным образом находим положение горизонталей на других сторонах квадрата. 4.8 мм

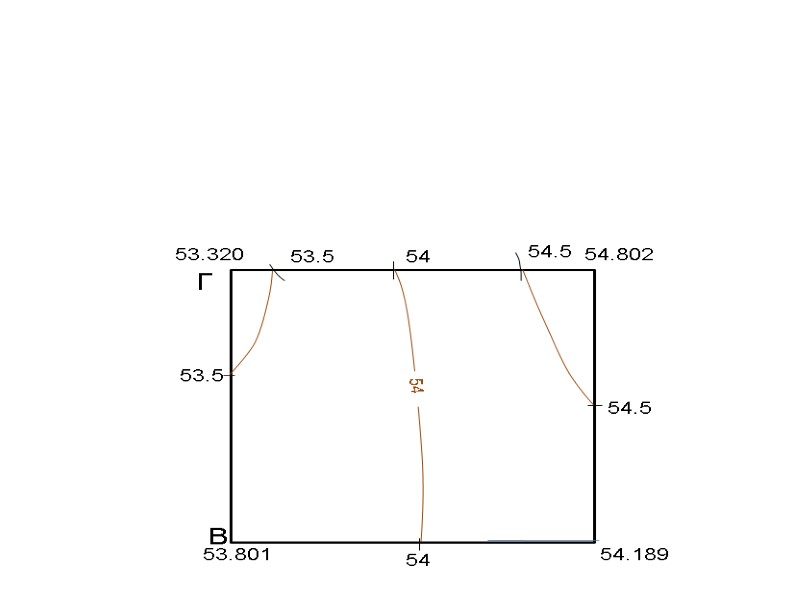

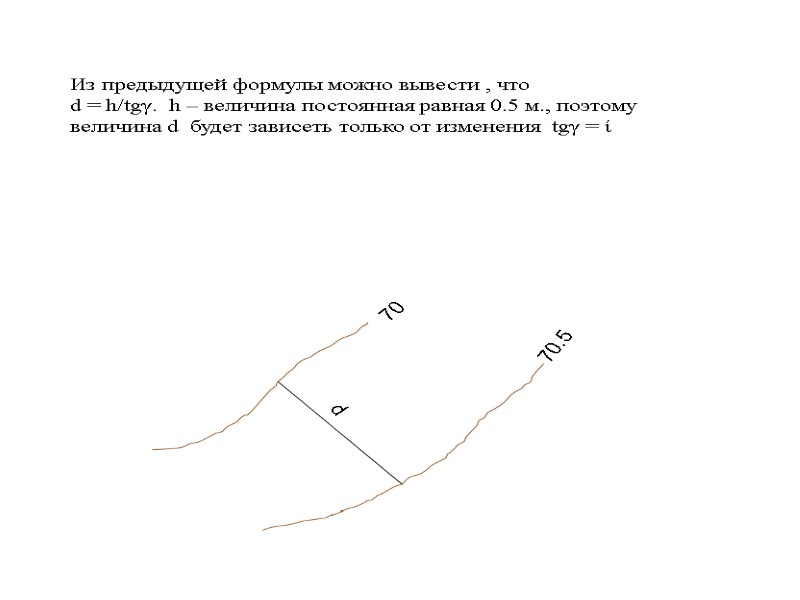


Под каждым отрезком подписываем значения углов наклона.

Ниже для наглядности, подпишем значения тангенсов этих углов или уклонов, но графики для углов и уклонов строятся раздельно.
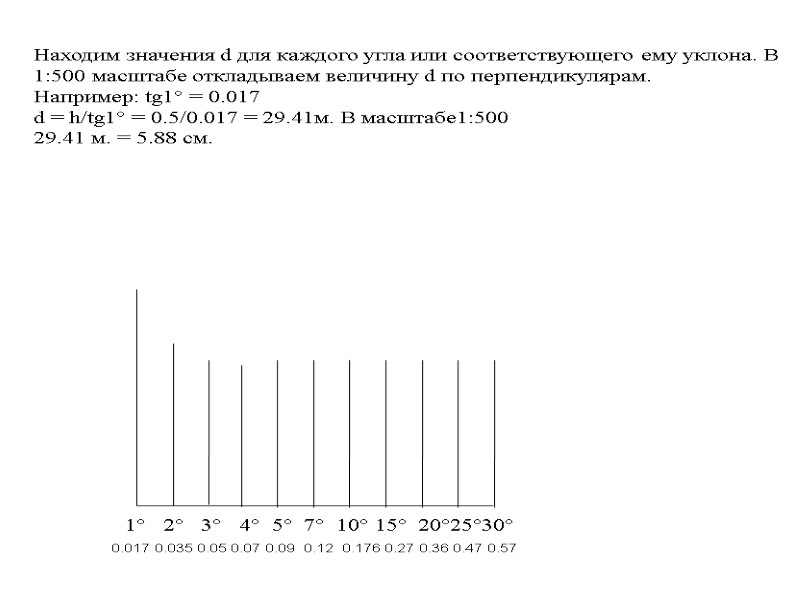
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Находим значения d для каждого угла или соответствующего ему уклона. В 1:500 масштабе откладываем величину d по перпендикулярам. Например: tg1° = 0.017 d = h/tg1° = 0.5/0.017 = 29.41м. В масштабе1:500 29.41 м. = 5.88 см.
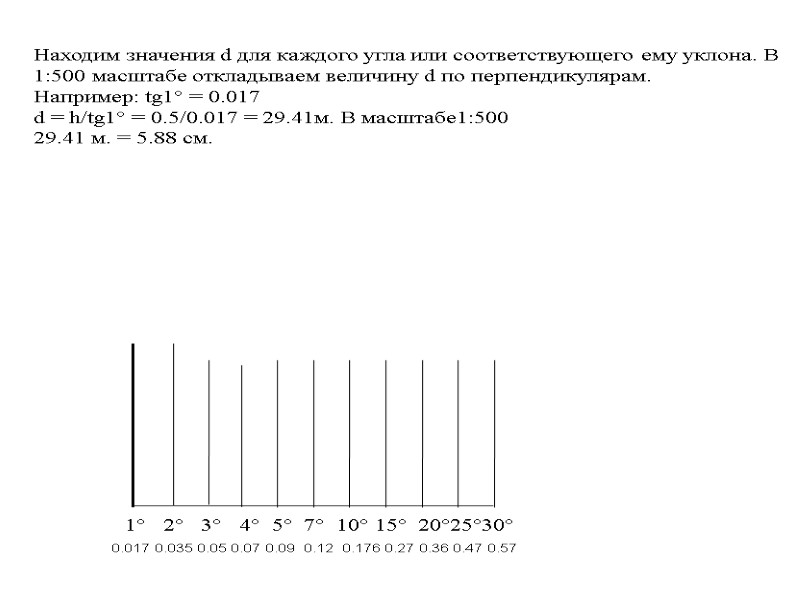
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Находим значения d для каждого угла или соответствующего ему уклона. В 1:500 масштабе откладываем величину d по перпендикулярам. Например: tg1° = 0.017 d = h/tg1° = 0.5/0.017 = 29.41м. В масштабе1:500 29.41 м. = 5.88 см.
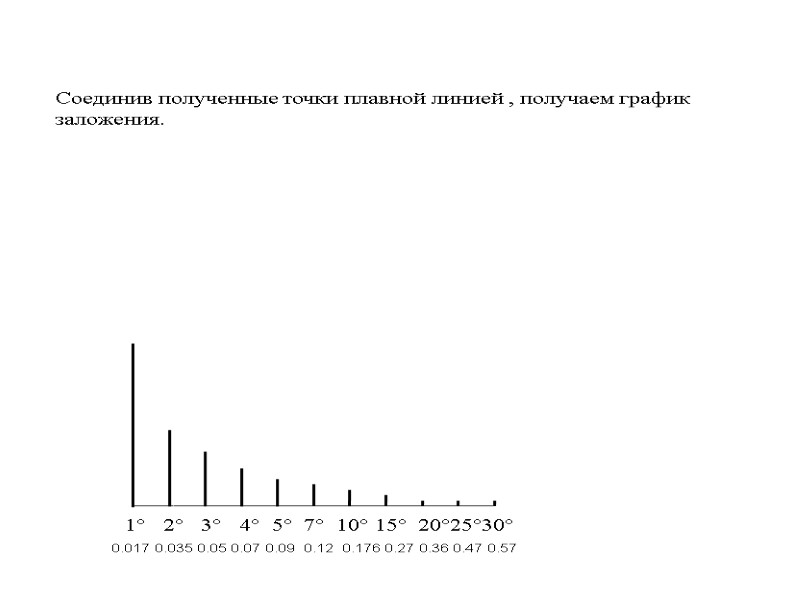
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Соединив полученные точки плавной линией , получаем график заложения.
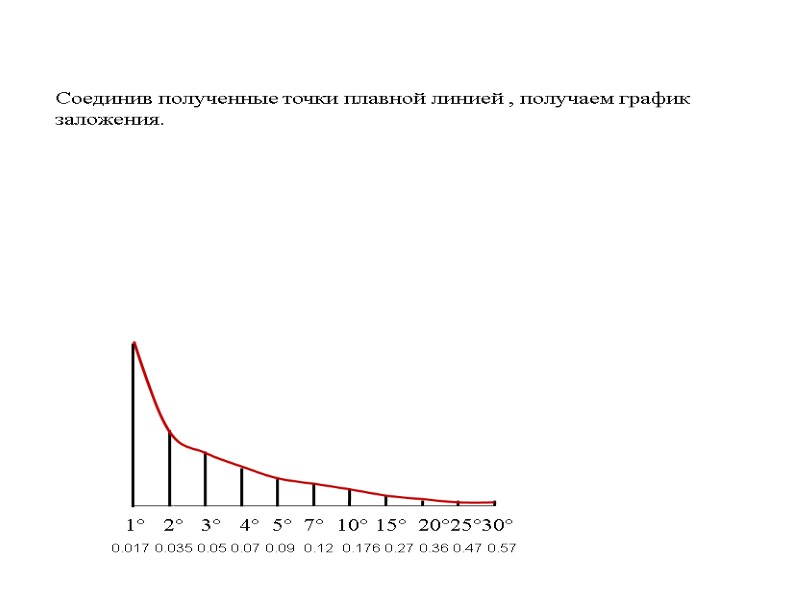
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Соединив полученные точки плавной линией , получаем график заложения.
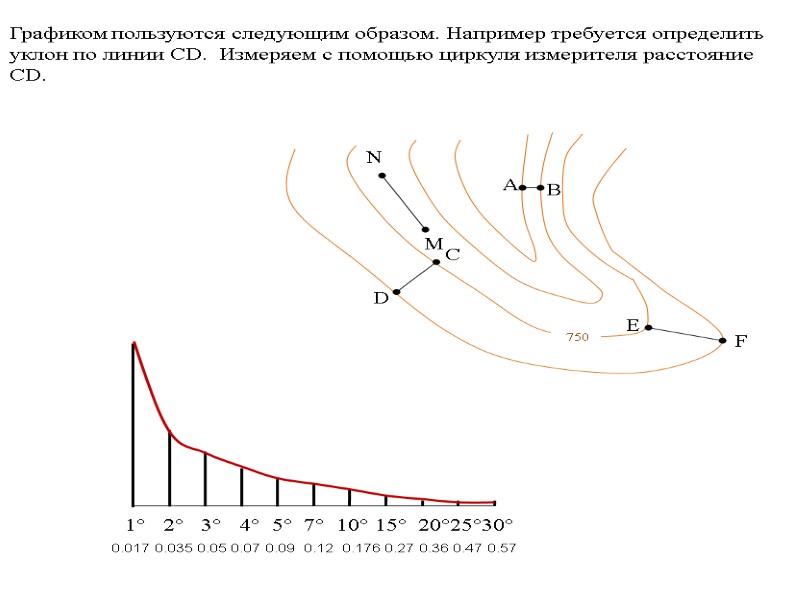
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Графиком пользуются следующим образом. Например требуется определить уклон по линии CD. Измеряем с помощью циркуля измерителя расстояние CD.
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57
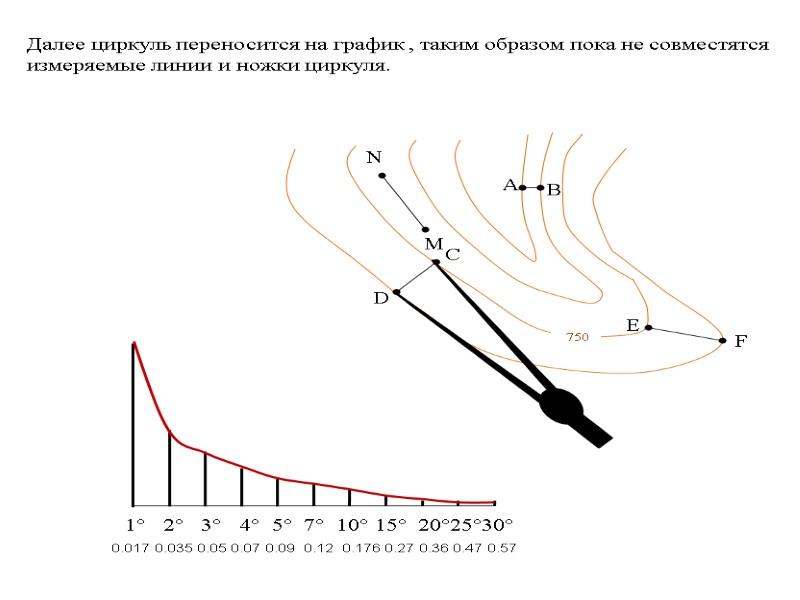
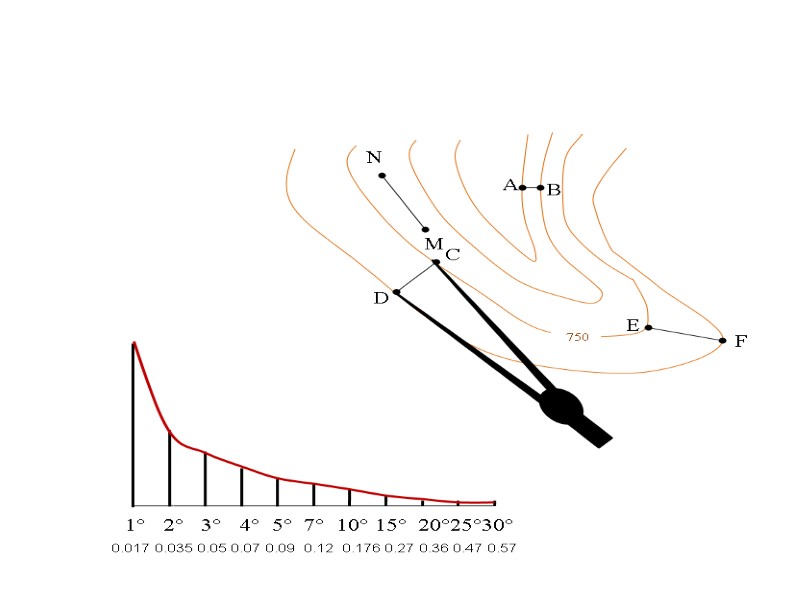
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Далее циркуль переносится на график , таким образом пока не совместятся измеряемые линии и ножки циркуля.
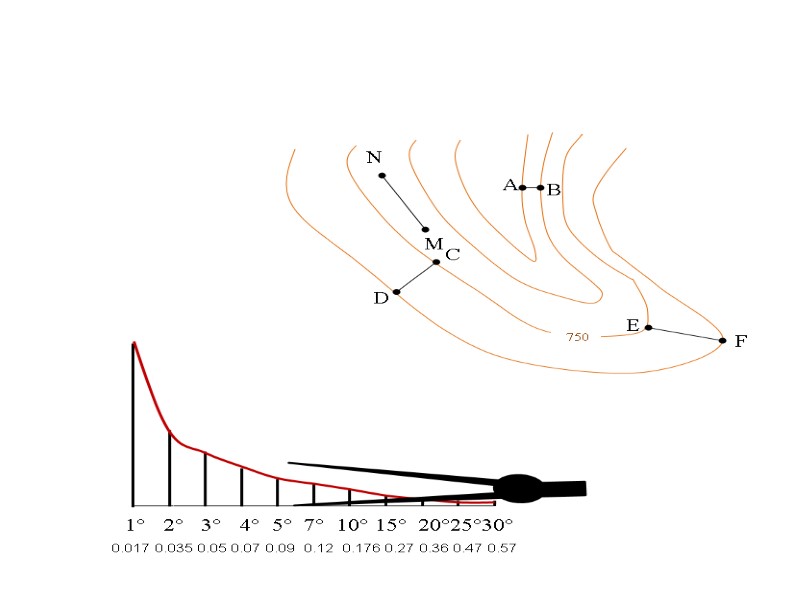
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57
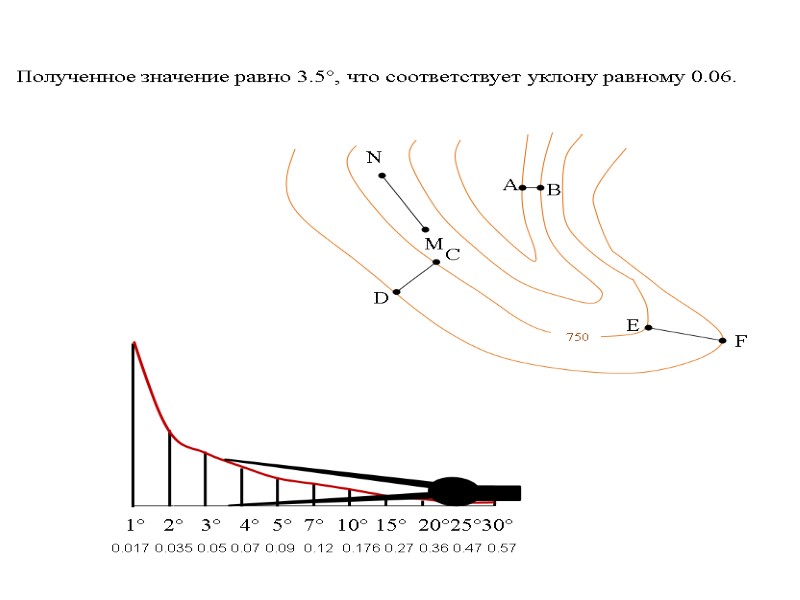
1° 2° 3° 4° 5° 7° 10° 15° 20°25°30° 0.017 0.035 0.05 0.07 0.09 0.12 0.176 0.27 0.36 0.47 0.57 Полученное значение равно 3.5°, что соответствует уклону равному 0.06.

Контрольные вопросы. Чему равен коэффициент дальномера ? Как определяется горизонтальное проложение? Сущность тахеометрической съемки? Порядок работы на станции при тахеометрической съемке? Что показывается на абрисе тахеометрической съемки? Как выносятся реечные точки на план тахеометрической съемки? Что такое горизонталь ? Как определяется крутизна ската? Назовите основные формы рельефа. Формула определения уклона ? Какие способы построение горизонталей вы знаете ? В чем сущность графического способа построения горизонталей? Как определяется положение горизонталей аналитическим способом? Для чего служат берг-штрихи? 15. Свойства горизонталей, как они подписываются ? 16. Для чего используются графики заложения ? 17. Как пользоваться графиком заложения?
7878-lektsia_6_str.ppt
- Количество слайдов: 166

