Task 1 The Language of Chance Words and

Task 1: The Language of Chance Words and phrases sure thing out of the question perhaps no doubt out of reach once in a blue moon most likely pig’s might fly possibly impossible maybe London to a brick safe bet no way long odds come rain or shine sporting chance long shot expected probably low risk shot in the dark unlikely doubtful definitely certain rock solid rarely you’ve got Buckley’s in the bag never What do these words and phrases mean? ten to one

Origins and Meanings of the Phrases of Probability Once in a blue moon Meaning: almost never, very seldom hardly ever Origin: when the moon is a crescent some people say the other part has a bluish colour to it. This ‘blue moon’ is rare. In the bag Meaning: certain of success, fixed, sure thing Origin: Game birds were used in fighting and were taken to the where they would fight in a bag. Owners of the birds would say to other competitors that victory was ‘in the bag’ meaning they were sure to win. We still use this expression to mean we are certain of success.

Task 1: The Language of Chance What is the chance of this happening? Match examples of situations and events to different likelihoods e. g. • Rain today • School will finish early • A police car will go past the school with its siren going • Lunch time will be extended • Lunch bell will go on time • Your family will win lotto • Someone will away in the class because they are sick • You will fall over in the playground and hurt yourself • You will eat your lunch • You will go to bed on time • It will be cloudy tomorrow • You will eat ice-cream for dessert tonight • Your favourite football team will win the grand final this year Which chance word or expression would you choose to represent the likelihood of these occurring? Can you think of another more suitable word? uncertain very likely very unlikely a good chance extremely likely in the bag maybe never pig’s might fly

Task 2: Collect all the Swap Cards The NEW brand of cereal has 6 new swap cards for you to collect. One in every packet. Investigation: How many packets of the new cereal would you have to buy in order to get one of each swap card? Number 1 2 3 4 5 6 Frequency Total Use the frequency table to keep a record of the results of your experiments. Numbers on the table can be changed to colours. How many packets would you need to buy to get one of each card? _______ Conduct the experiment 20 times. What is the average number of boxes you would need to buy? ______

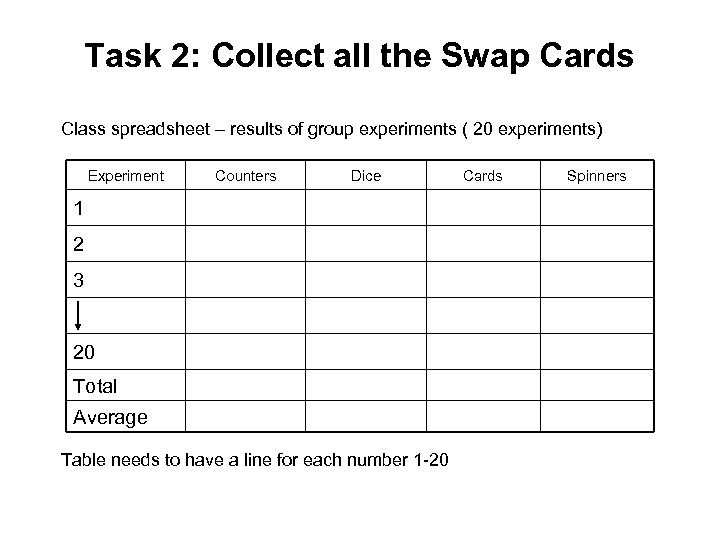Task 2: Collect all the Swap Cards Class spreadsheet – results of group experiments ( 20 experiments) Experiment Counters Dice 1 2 3 20 Total Average Table needs to have a line for each number 1 -20 Cards Spinners

Task 3: Lucky Number Game Good luck! 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Pick your favourite numbers: What chance do you think you have of picking the selected numbers? ! 1 number __________ 2 numbers _________ 3 numbers _________ 4 numbers _________

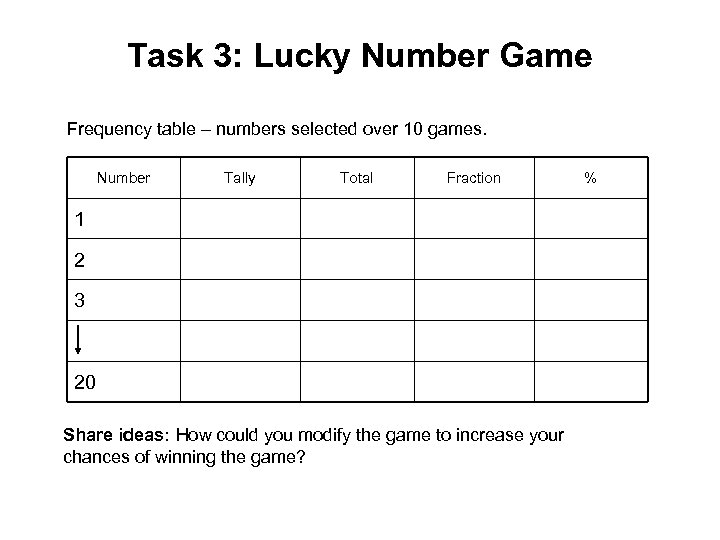Task 3: Lucky Number Game Frequency table – numbers selected over 10 games. Number Tally Total Fraction 1 2 3 20 Share ideas: How could you modify the game to increase your chances of winning the game? %

How to Make Your Own Spinner Steps to follow: 1. Colour your spinner according to the given instructions. 2. Place a paperclip on the spinner in the centre of the circle. Use a pencil to hold the paperclip in place. The paperclip should be able to spin around 360 degrees. 3. Flick the paper clip and note where the paper clip lands.

Student Guide: How To Simplify Fractions Keys used: Numerator Denominator Simp Example: Simplify 18/24 Steps to follow: Press Display 1. 18 24 8/24 1. 2. 18/24 S 2. 3. 18/24 S 9/12 3. 4. 9/12 S ¾ Note: You may need to press and more than once to get the fraction to its simplest form.

Student Guide: Converting a Fraction to a % Example: Convert 6/40 to a % Steps to follow: Press Display 1. 6 40 6/40 1. 2. 6/40 2. 3. Keys used: Numerator Denominator Percentage Key Enter 15% % Note: arrow represents cursor on display

Student Guide: Store to Memory and Memory Recall Keys Packets of cereal Tally Frequency 12 IIII 4 13 III 3 14 IIII 4 15 III 3 Steps to calculate the average/mean: Press Display 4 x 12 = 48 (need a m above 12) 3 x 13 = 39 (need a m above 13) 4 x 14 = 56 (need a m above 14) 3 x 15 = 45 (need a m above 15 ) (Recall total) 188 (m above 188) 188 ÷ 14 = 13. 4 Note: If you then press the key twice it will clear the memory.