Talk Summary Using Statistics

Talk Summary • • • • Using Statistics To Make Inferences 1 • Using Statistics Preliminaries • Summary of Week 1 • Practical – The Vietnam Draft • What might we test? Sampling • Notation • Sampling Distributions Testing Hypothesis • Significant • One Tail Test • Accepting Or Rejecting The Null Hypothesis - p • -Value • Interpretation Of p-Values Review The Steps Involved In Finding A p Value What Does It Mean? What is the average height of 19 year old males? What is the average weight of female students? Is there any evidence for extra-sensory perception? Does alcohol slow down reaction times? Does a new method of teaching mathematics improve scores? Suggested Texts Read Practical 1 Best Access Route Whoops! 1. 1

Using Statistics To Make Inferences 1 Each week I usually discuss a single test. During the tutorial, that follows the lecture, you can explore the test within SPSS and also consider additional traditional examples from past examinations. It is advisable to print out the slides (and statistical tables from the printer friendly version) to annotate during the lecture. I have done this for you this week. Stacey’s Statistical Supplements (administered by Maths Aid) are intended as take home exercises, bring queries next week. There are more resources located there that you might find helpful. 1. 2 2 15 March 2018 3: 58 PM

Maths-Aid • Maths or Stats problems? Need help? • Maths-Aid is a drop-in centre providing a free and confidential service to all non-Maths&Stats UG and PGT students of Newcastle University • We are dedicated to providing professional assistance and advice on all aspects of mathematics and statistics including: • preparation for exams • developing problem solving and numerical skills • explanation of concepts and methods • help in understanding lecture notes Maths-Aid is based in the Robinson Library, Room 201, Level 2 www. ncl. ac. uk/ask/where-to-go/maths-aid Drop-in, 12. 45 pm – 4. 00 pm, Monday-Thursday (term-time) (we’re also open on Fridays during the assessment and resit periods)

Using Statistics Preliminaries How are your numeracy skills? Are you adept with your calculator? Why not take a basic test. If you experience problems ask for help during the tutorial. Even the media are aware Some detailed notes are available. 1. 4 4

Using Statistics To Make Preliminaries How are your high school statistics skills? Practical Statistics - Mary Rouncefield and Peter Holmes - 1989 Published by Palgrave Macmillan, but currently out of print. Available at Robinson Books Level 3 (519. 5 ROU ). This is a text aimed at high school students. It is widely (and cheaply) available in the second hand market (try a search in your favourite browser). Their alternate texts are more expensive Mastering Statistics and Making Sense of Statistics. 1. 5 5

Summary of Week 1 Summary What is an experiment What is an hypothesis What is a p-value 1. 6 6

Practical – The Vietnam Draft This is modern history as captured in film. The practical explores a real world example of a poor survey that cost lives! 1. 7 7

What might we test? 1. Men are taller than women 2. Women are taller than men 3. Men and women are the same height 1 & 2 are typical examples of a one tail test (< or >). 3 is a typical example of a two tail test for equality(=). As opposed to not equal to (≠). 1. 8 8

What might we test? Always plot your data. However be wary of a histogram with a “frequency” axis. 1. 9 9

What might we test? 1. 2. 3. 4. Men are more competitive than women are. Women are more co-operative than men are. Lung cancer is more common among smokers. 80% of traffic accidents are caused by excessive speed. 5. Colour blindness is more common among men. 6. Men find women with a smaller waist to hip ratio more attractive. Any problems? 1. 10 10

What might we test? 7. Women find men with more symmetric features more attractive. 8. 87% of the population support the present Prime Minister. 9. More young people are vegetarians. 10. Children are more likely to be killed by stepfathers than fathers. 11. 67% of people own mobile phones. Any problems? 1. 11 11

What might we test? 12. Students are more likely than staff to own mobile phones. 13. Poorer people commit more crimes. 14. Extroverts are more successful. 15. 32% surveyed prefer organically grown vegetables. Any problems? 1. 12 12

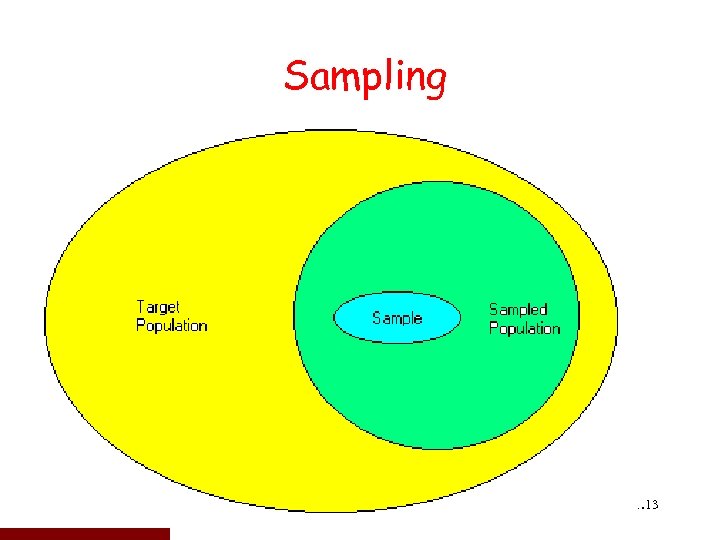Sampling 1. 13 13

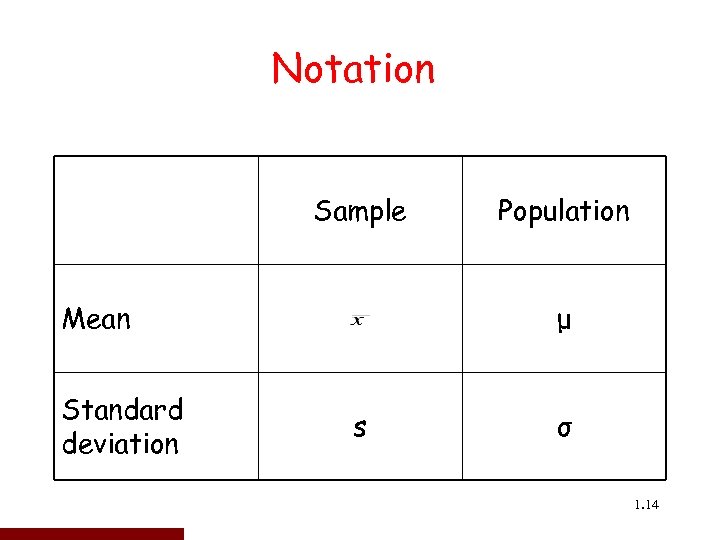Notation Sample Mean Standard deviation Population μ s σ 1. 14 14

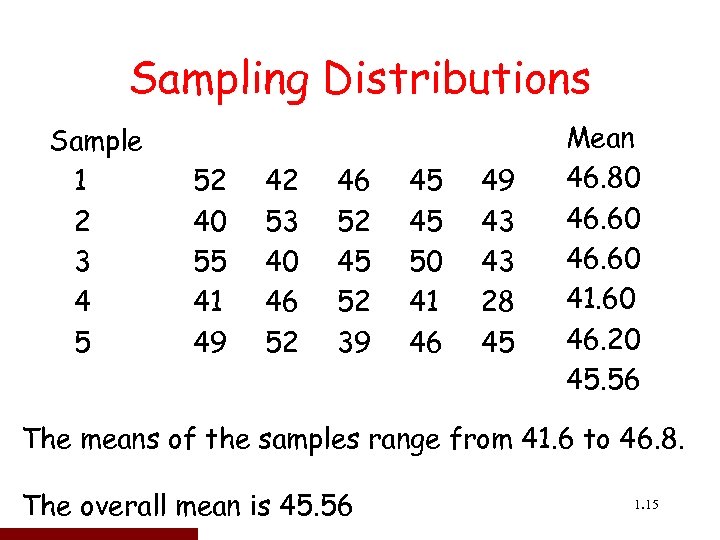Sampling Distributions Sample 1 2 3 4 5 52 40 55 41 49 42 53 40 46 52 45 52 39 45 45 50 41 46 49 43 43 28 45 Mean 46. 80 46. 60 41. 60 46. 20 45. 56 The means of the samples range from 41. 6 to 46. 8. The overall mean is 45. 56 1. 15 15

Testing Hypothesis Null hypothesis Alternate hypothesis H 0 Assumes that there is no real effect present H 1 Assumes that there is some effect 1. 16 16

Testing Hypothesis Recall that a null hypothesis (Ho) states that the findings of the experiment are no different to those that would have been expected to occur by chance. Statistical hypothesis testing involves calculating the probability of achieving the observed results if the null hypothesis were true. If this probability is low (conventionally p < 0. 05), the null hypothesis is rejected and the findings are said to be “statistically significant” (unlikely) at that acceptance level. A p of. 05 means there’s a less than 5 percent chance that in the world where the null hypothesis is true, the results you’re seeing would be due to random chance. 1. 17 17

Significant One outcome of our analysis is that the results we obtained are reliable. If we were to collect more data, we would find the same thing. In this case we refer to the results as being statistically significant. The term significant is unfortunate in this context because in research the word does not mean important. When Ronald fisher invented the F-test and our current approach to statistics, he chose the word “significant” to suggest that the results signified that something interesting happened. Fisher, R. A. (1922). On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society of London, A, 222, 306– 368. Fisher, R. A. (1955). Statistical methods and scientific induction. Journal of the Royal Statistical Society, B, 17, 69– 78. 1. 18 18

Significant Today we use the word differently, we use significant to mean important. But statistically significant results are not always important. While a rise in the average IQ score for local school children in a year might be significant it would hardly be important to most of us. 1. 19 19

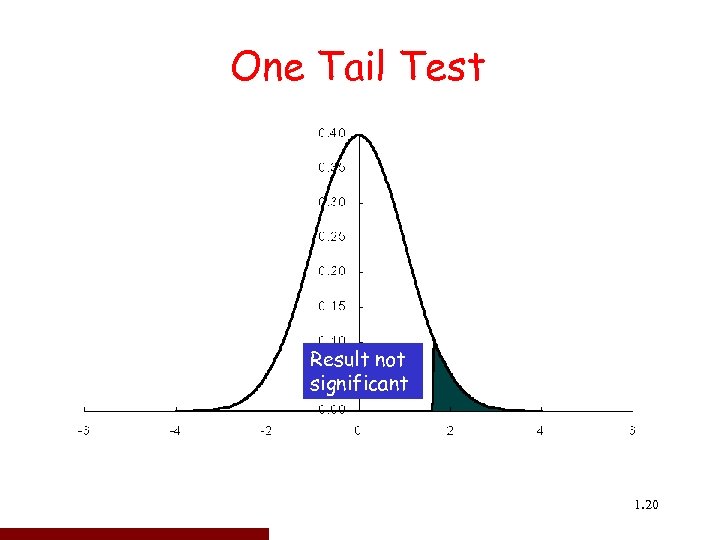One Tail Test Result not 95% Accept H 0 significant C 0: µ ≤ µ 1 - less than H Cc 1: µ > µ 1 – greater than H 1. 20 20

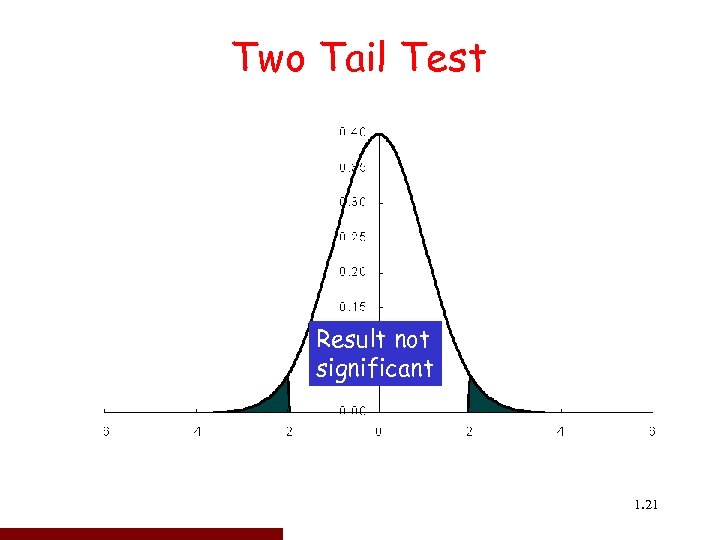Two Tail Test Result not 0 Accept H 95% significant C Cc H 0: µ 2 ≤ µ 1 - lies between the bounds H 1: µ > µ 1 or µ < µ 2 – lies outside the bounds 1. 21 21

Accepting Or Rejecting The Null Hypothesis - p-Value p-value p>0. 1>p>0. 05 Significance Not significant at the 10% level Decision Accept H 0 Significant at the 10% level, Accept H 0, investigate but not at 5% further 0. 05>p>0. 01 Significant at the 5% level Reject H 0 0. 01>p>0. 001 Significant at the 1% level Reject H 0, with some confidence Significant beyond the 0. 1% level Reject H 0, with reasonable certainty 0. 001>p 1. 22 22

Interpretation Of p-Values A commentary on p values 1. 23 23

Review The Steps Involved In Finding A p Value 1. We formulate a null hypothesis. 2. Assuming the null is true, we employ that null model. 3. We superimpose the null model on our sample data (usually a statistic like t or chi square). 4. We find the area(s) in the null model that are as extreme or more extreme than our sample data. 5. That extreme area is the p value. 1. 24 24

What Does It Mean? The p value represents the area in the null model that is more extreme than our sample data given we assume the null is true. A large p value means that our sample data do not look unusual given the null model. A very low p value suggests a misfit between our data and the null model. 1. 25 25

What Does It Mean? The smaller the p value is, the more discrepant our sample results look, compared to what they should look like under the null model. What does the p value prove? Actually nothing. If we retain the null with a large p value, it does NOT prove that the null is true. If we reject the null with a low p value it does NOT prove that the null is false. 1. 26 26

What Does It Mean? At best, low p values suggest to you that the null model is not looking too good since the sample data conflict with it. Does rejecting the null tell you how strong an effect is? NO Does rejecting the null tell you how important an effect is? NO 1. 27 27

What Does It Mean? The report, based on contributions from 26 ASA experts, enunciates six main principles, with discussion of each. The principles are listed below. 1. p-values can indicate how incompatible the data are with a specified statistical model. 2. p-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone. 3. Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold. 4. Proper inference requires full reporting and transparency. 5. A p-value, or statistical significance, does not measure the size of an effect or the importance of a result. 6. By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis. The ASA's Statement on p-Values: Context, Process, and Purpose Ronald L. Wasserstein and Nicole A. Lazar The American Statistician 2016 70(2) 129 -133 DOI: 10. 1080/00031305. 2016. 1154108 1. 28 28

What is the average height of 19 year old males? Type of study parameter estimation Sample 10 members of the class Sampling method choose at random Population students studying PSY 1011 Type of population finite 19 year old males Target population not of UK 19 year olds in general, only first year psychology students 1. 29 29

What is the average weight of female students? Type of study parameter estimation Sample 10 members of the class Sampling method ask for volunteers Population students studying PSY 1011 Type of population finite all female students Target population not of female students in general, only first year psychology students 1. 30 30

Is there any evidence for extra-sensory perception? Method Test whether an individual has extra-sensory perception, by identifying the shape, from five possible, on a concealed card. Infinite population Repeat to obtain a sample of the required size. Random variable Number of successful predictions. Null hypothesis If guessing should be correct one time in 5. If there were 12 correct response in 50 trials, would this be sufficient evidence for extra-sensory perception? See the Binomial section later. 1. 31 31

Does alcohol slow down reaction times? Method Choose a representative sample. Run experiment One group is given alcohol, the control group a placebo, both are presented with an identical stimulus and their reaction times recorded. Test Do reaction times differ between the groups. Method Choose a representative sample. The appropriate method of analysis will be covered later. 1. 32 32

Does a new method of teaching mathematics improve scores? The average score obtained by all children completing a mathematics test is 56%. In an experiment 100 children, selected at random, are taught by a novel method and their scores noted. To test the result either estimate the sample average score together with a confidence interval or test whether the average score differs significantly from the national average. The appropriate method of analysis will be covered later. 1. 33 33

Suggested Texts • Introduction to Statistics in Psychology by Dennis Howitt and Duncan Cramer, ISBN: 0130173142 • First Steps In Research and Statistics: A Practical Workbook for Psychology Students by Dennis Howitt and Duncan Cramer, ISBN 0203457323 (electronic book) 0415201012 • Statistics For The Behavioural Sciences An Introduction by Riccardo Russo, ISBN 0203641574 (electronic book) 1841693200 • An Introduction to Statistics and Research Methods: Becoming a Psychological Detective by Stephen F. Davis and Randolph A. Smith, Prentice Hall, ISBN 0131505114 1. 34 34

Read Howitt and Cramer pages 3 -8 Read Howitt and Cramer (e-text) pages 3 -8 Read Russo pages (e-text) 78 -94 Read Davis and Smith pages 14 -15, 42 -43 1. 35 35

Practical 1 This material is available from the module web page. Module Web Page http: //www. staff. ncl. ac. uk/mike. cox 1. 36 36

Practical 1 This material for the practical is available. Instructions for the practical Practical 1 http: //www. staff. ncl. ac. uk/mike. cox/PSY 1011/story 1. pdf Material for the practical Practical 1 http: //www. staff. ncl. ac. uk/mike. cox/PSY 1011/1. sav 1. 37 37

Best Access Route For technical reasons the best performance for the material (SPSS and e-books) used in this module is obtained using a web page via RAS. Enter ras. ncl. ac. uk into your favourite web browser. 1. 38 38

Best Access Route Then select Communications and Browsers > IE For on Campus Web Pages and enter www. staff. ncl. ac. uk/mike. cox in the available address box 1. 39 39

Best Access Route 1. 40 40

Best Access Route 1. 41 41

Best Access Route 1. 42 42

Best Access Route 1. 43 43

Best Access Route 1. 44 44

Best Access Route For Software Such As SPSS 1. 45 45

Best Access Route 1. 46 46

Best Access Route 1. 47 47

Best Access Route 1. 48 48

Whoops! Experts disagree over the issue, with some saying there is no proof light drinking harms the baby, while others believe the evidence is inconclusive. The Independent 21 January 2009 1. 49 49

Whoops! Why pay less when you could pay more? 1. 50 50

Whoops! Obamacare turns a simple math question into a complex equation nobody seems able to solve An hour-long Facebook debate started when one person posted this image and pointed out that the math in it was incorrect. 360, 000 (dollars) ÷ 317, 000 (people) = 1. 1356 (dollars person) 1. 1356 rounds up to $1. 14, or down to $1. 13 if rationing out an actual limited amount of money 1. 51 51

1. 52 52