Tale about the analysis of the production 2

Tale about the analysis of the production 2

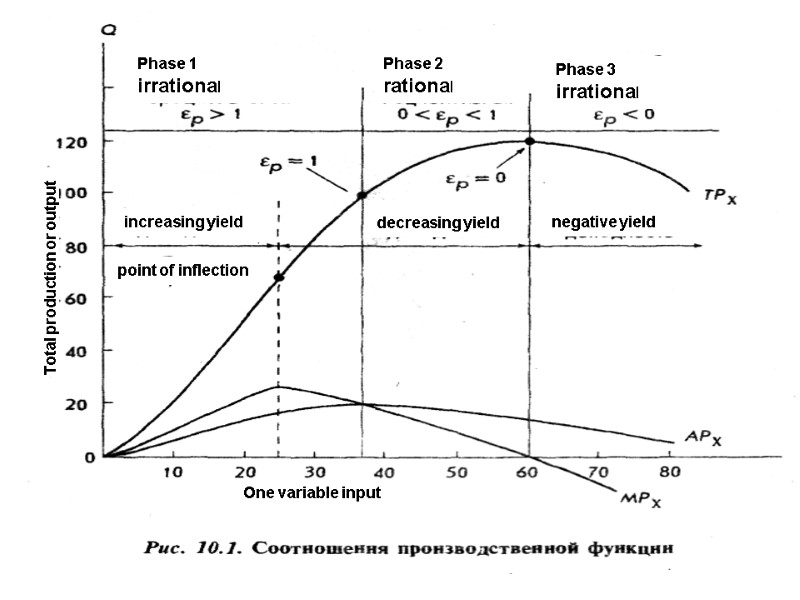
The production as some function of the level of output depending on one variable input factor in the production while maintaining all other inputs constant Goal: to understand the productivity of factors of production and its influence on the production function Consider a production system with two variable inputsпроизводства

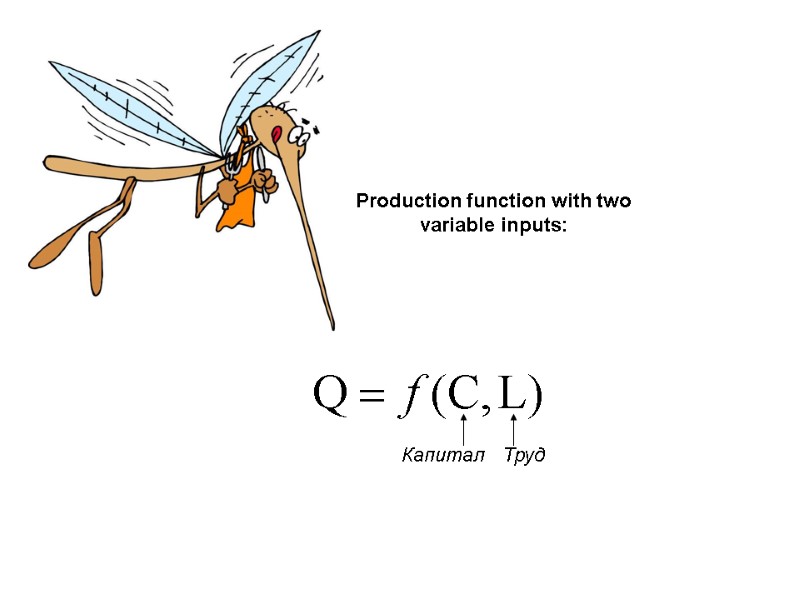
Production function with two variable inputs: Капитал Труд

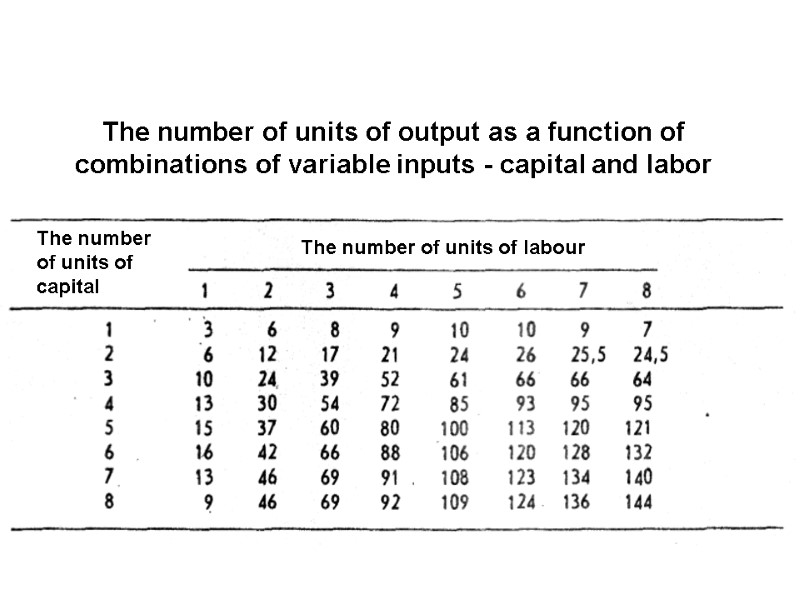
The number of units of output as a function of combinations of variable inputs - capital and labor The number of units of labour The number of units of capital

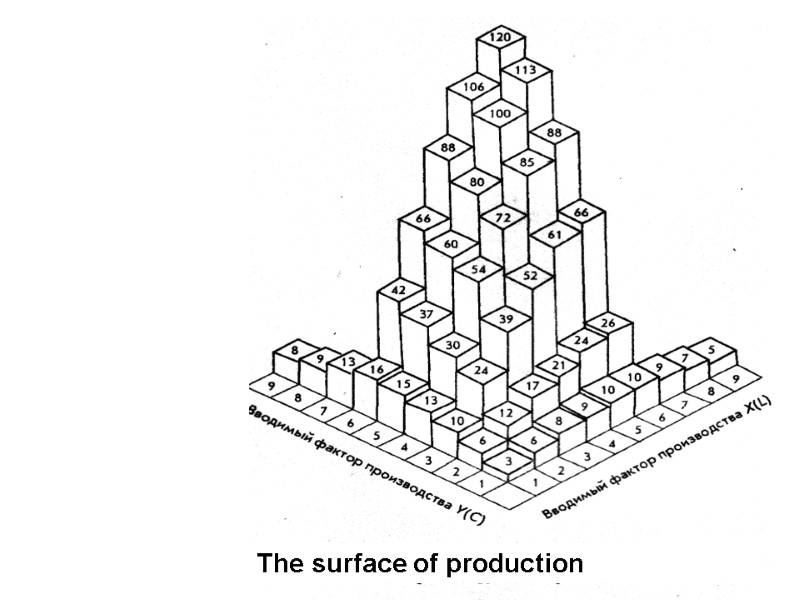
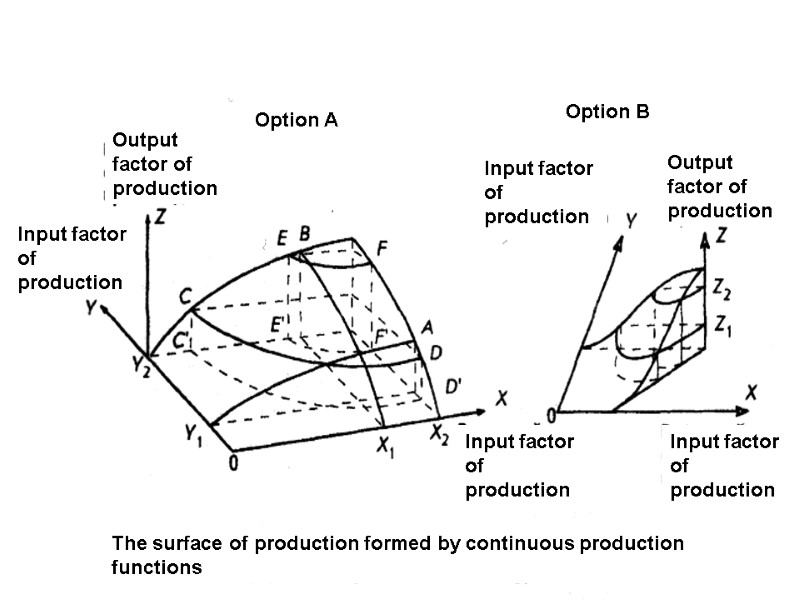
The surface of production

The main characteristics of the isoquants are the same as those of indifference curves: the number is infinite, continuous MRTSxy = - ∆Y / ∆X Input factor of production X (labour) Input factor of production Y(capital) Isoquants The slope of the curve determines the marginal rate of technical substitution

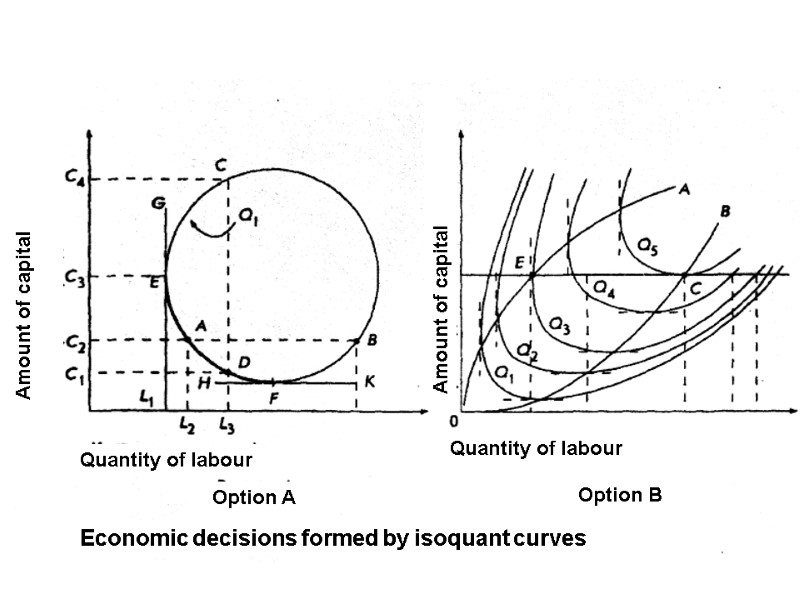
Economic decisions formed by isoquant curves Option A Option B Quantity of labour Quantity of labour Amount of capital Amount of capital

The rule of minimum cost

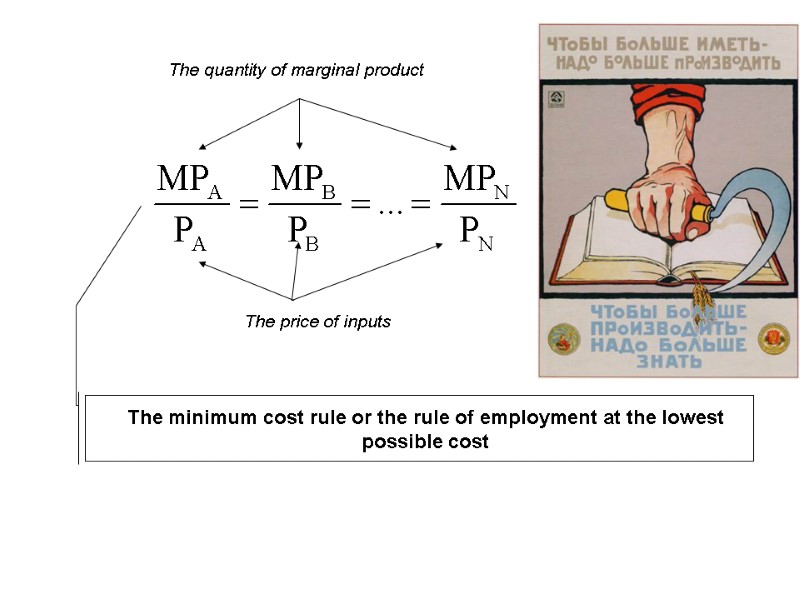
The quantity of marginal product The price of inputs The minimum cost rule or the rule of employment at the lowest possible cost

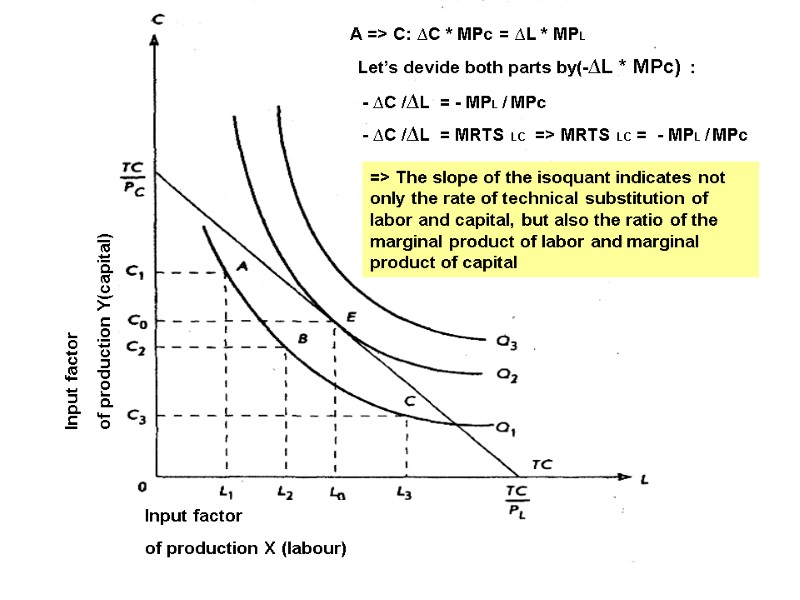
А => С: ∆С * МРс = ∆L * MPL Let’s devide both parts by(-∆L * МРс) : - ∆С /∆L = - MPL / МРс - ∆С /∆L = MRTS LC => MRTS LC = - MPL / МРс => The slope of the isoquant indicates not only the rate of technical substitution of labor and capital, but also the ratio of the marginal product of labor and marginal product of capital Input factor of production X (labour) Input factor of production Y(capital)

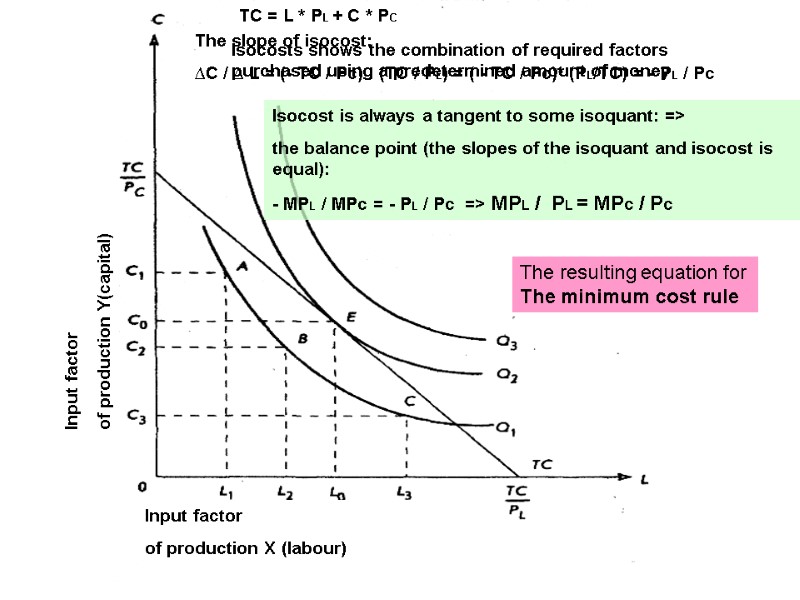
Isocosts shows the combination of required factors purchased using a predetermined amount of money TC = L * PL + C * PC The slope of isocost: ∆С / ∆ L = (- TC / Pc) : (TC / PL) = ( - TC / Pc)* (PL/TC) = - PL / Pc Isocost is always a tangent to some isoquant: => the balance point (the slopes of the isoquant and isocost is equal): - MPL / МРс = - PL / Pc => MPL / PL = МРс / Pc The resulting equation for The minimum cost rule Input factor of production X (labour) Input factor of production Y(capital)

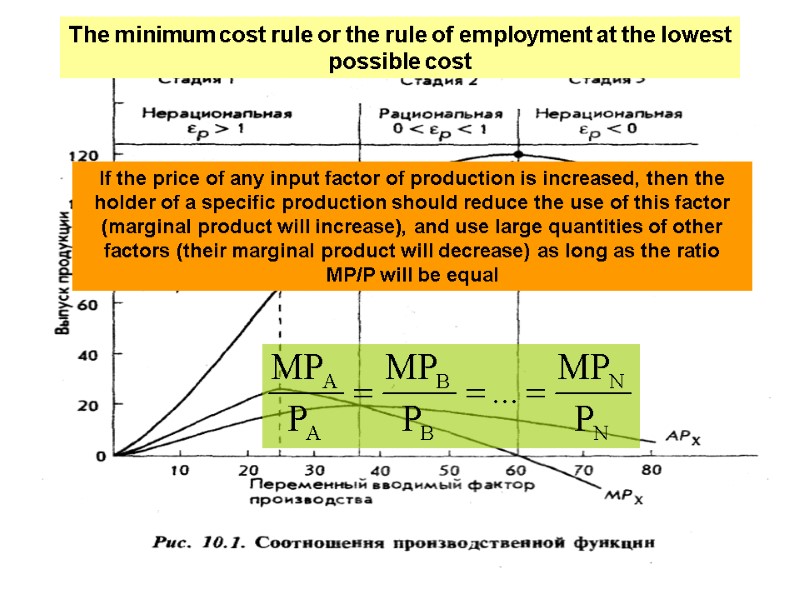
The minimum cost rule or the rule of employment at the lowest possible cost If the price of any input factor of production is increased, then the holder of a specific production should reduce the use of this factor (marginal product will increase), and use large quantities of other factors (their marginal product will decrease) as long as the ratio MP/P will be equal