ПОИСК РЕШЕНИЯ-правильная.ppt
- Количество слайдов: 20

Табличный процессор EXCEL решения задач линейного программирования с помощью команды «Поиск решения»

Команда Поиск решения Для решения сложных задач, требующих приме- нения линейного и нелинейного программирова- ния, а также методов исследования операций применяется надстройка - Поиск решения. Чтобы использовать надстройку Поиск решения не обязательно знать методы программирования и исследования операций, но необходимо определять, какие задачи можно решать этими методами. Пользователь должен уметь с помощью диалого- вых окон надстройки Поиск решения правильно сформулировать условия задачи, и если решение существует, то “Поиск решения” отыщет его. В основе надстройки лежат итерационные методы.

Команда Поиск решения В том случае, когда оптимизационная задача содержит несколько переменных величин, для анализа сценария необходимо воспользоваться надстройкой Поиск решения. “Поиск решения” позволяет использовать одновременно большое количество изменяемых ячеек (до 200) и задавать ограничения для изменяемых ячеек.

Команда Поиск решения Общие свойства, которые характерны для задач, решаемых с помощью «Поиск решения» : n Существует единственная целевая ячейка, содержащая формулу, значение которой должно быть сделано максимальным, минимальным или же равным, какому-то конкретному значению. n Формула в этой целевой ячейке содержит ссылки на ряд изменяемых ячеек. Поиск решения заключается в том, чтобы подобрать такие значения переменных в изменяемых ячейках, которые бы обеспечили оптимальное значение для формулы в целевой ячейке. n Может быть задано некоторое количество ограничений — условий или соотношений, которым должны удовлетворять некоторые из изменяемых ячеек.

Постановка задачи Первым шагом при работе с командой «Поиск решения» является создание специализированного листа. Для этого необходимо создать целевую ячейку, в которую вводится основная формула. Кроме того, лист может включать другие значения и формулы, использующие значения целевой и переменных ячеек. Формула в целевой ячейке должна опираться в вычислениях на значения переменных ячеек.

После того, как задача оптимизации будет подготовлена на листе, можно приступать к работе. Необходимо: 1. Выделить на листе целевую ячейку, в которую введена формула. 2. Выполнить команду Сервис/Поиск решения. Открывается окно диалога Поиск решения. Поскольку была выделена ячейка, в текстовом поле «Установить целевую ячейку» появится правильная ссылка на ячейку. В группе «Равной» переключатель по умолчанию устанавливается в положение «Максимальному значению» .
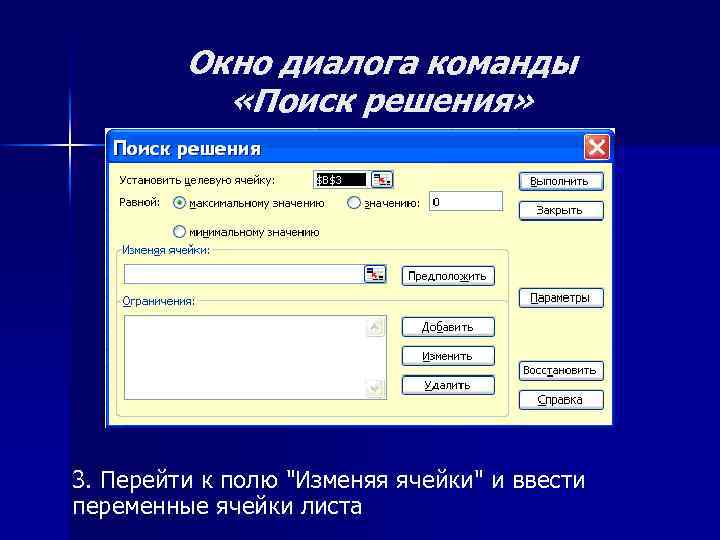
Окно диалога команды «Поиск решения» 3. Перейти к полю "Изменяя ячейки" и ввести переменные ячейки листа
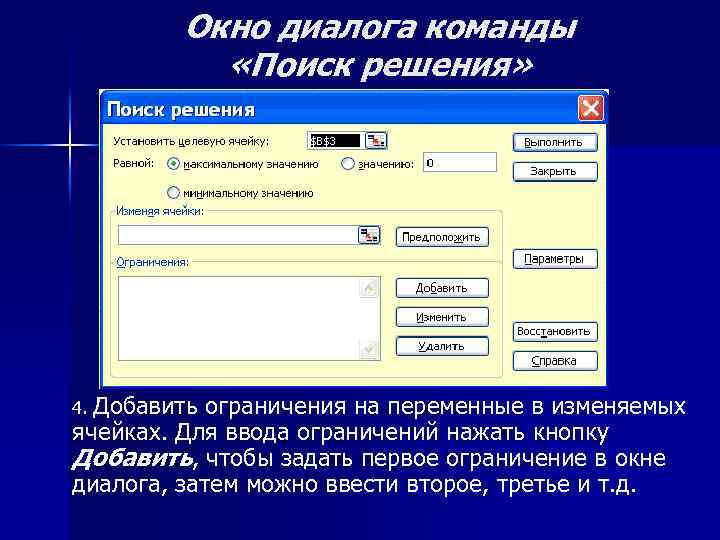
Окно диалога команды «Поиск решения» 4. Добавить ограничения на переменные в изменяемых ячейках. Для ввода ограничений нажать кнопку Добавить, чтобы задать первое ограничение в окне диалога, затем можно ввести второе, третье и т. д.
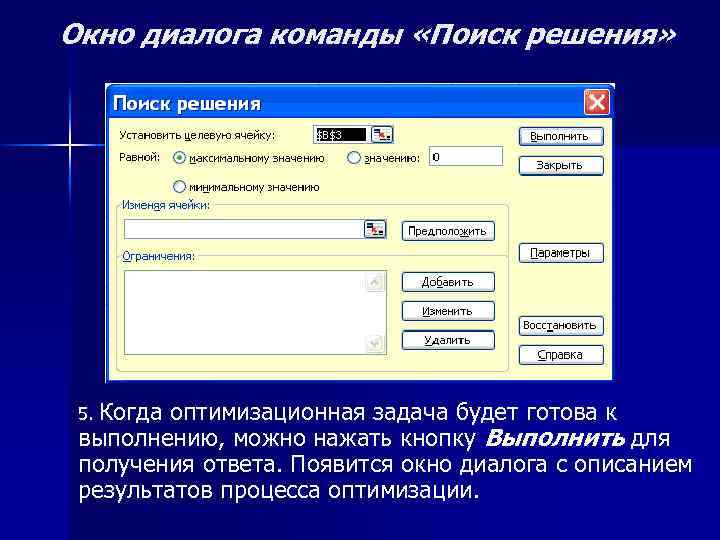
Окно диалога команды «Поиск решения» 5. Когда оптимизационная задача будет готова к выполнению, можно нажать кнопку Выполнить для получения ответа. Появится окно диалога с описанием результатов процесса оптимизации.
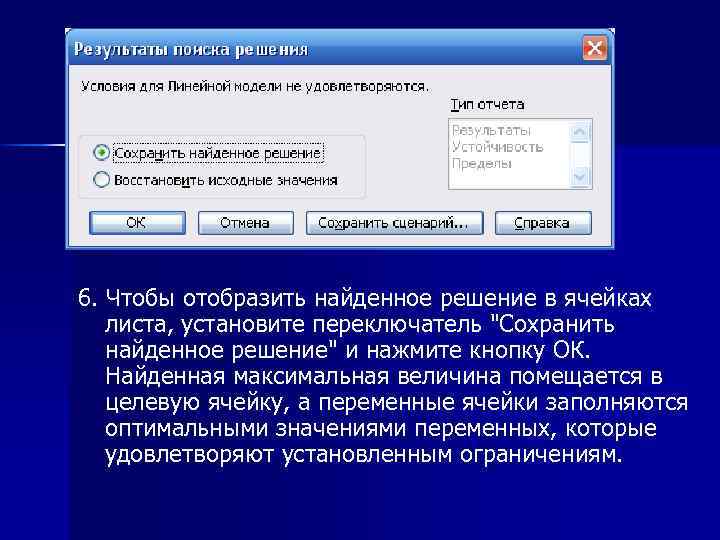
6. Чтобы отобразить найденное решение в ячейках листа, установите переключатель "Сохранить найденное решение" и нажмите кнопку ОК. Найденная максимальная величина помещается в целевую ячейку, а переменные ячейки заполняются оптимальными значениями переменных, которые удовлетворяют установленным ограничениям.

ПОИСК РЕШЕНИЯ Предположим, что на предприятии решили производить несколько видов конфет. Назовем их условно "A", "B" и "C". Известно, что реализация 10 -и килограмм конфет "А" дает прибыль 9 $, "В" - 10 $ и "С" - 16 $. Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной.
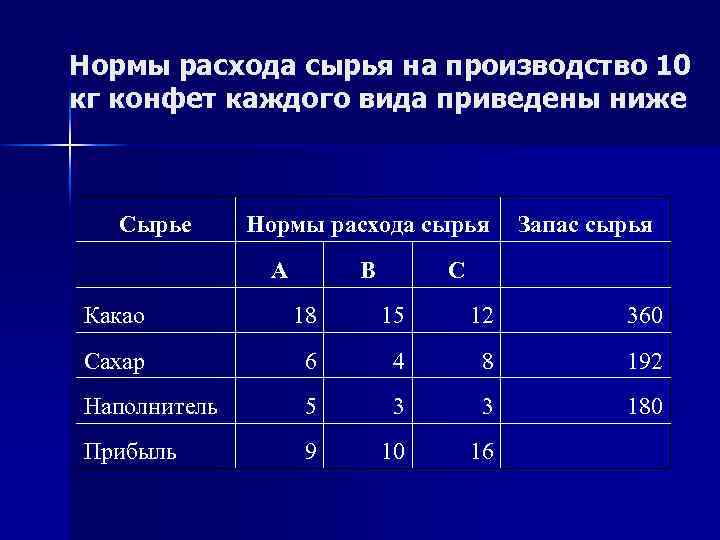
Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже Сырье Нормы расхода сырья А В С Запас сырья Какао 18 15 12 360 Сахар 6 4 8 192 Наполнитель 5 3 3 180 Прибыль 9 10 16

Для решения задачи необходимо подготовить специальный лист EXCEL. Исходные данные и формулы ввести в электронную таблицу, как указано ниже. Целевая функция [прибыль] Ограничения на целевую функцию
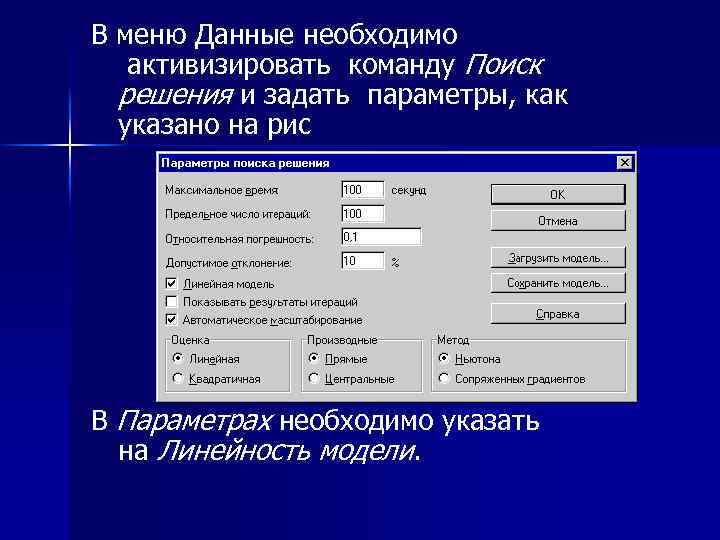
В меню Данные необходимо активизировать команду Поиск решения и задать параметры, как указано на рис В Параметрах необходимо указать на Линейность модели.
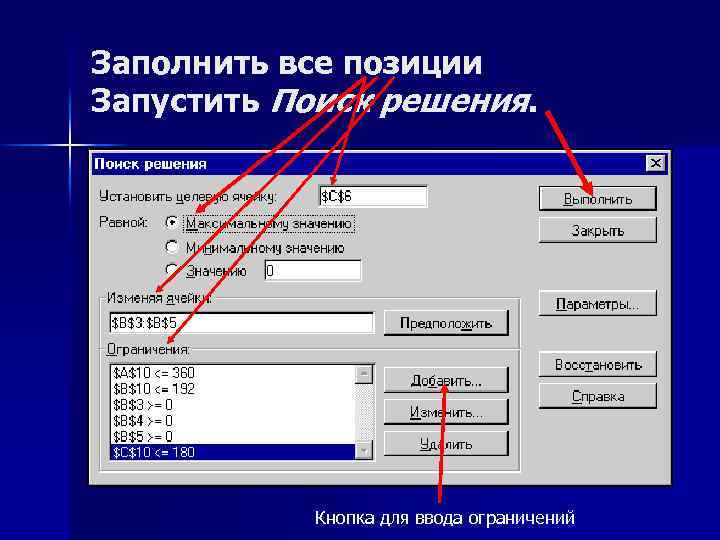
Заполнить все позиции Запустить Поиск решения. Кнопка для ввода ограничений
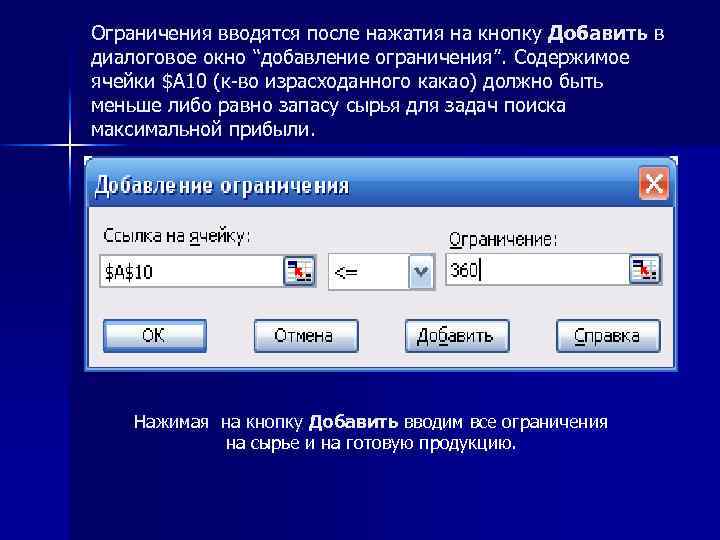
Ограничения вводятся после нажатия на кнопку Добавить в диалоговое окно “добавление ограничения”. Содержимое ячейки $A 10 (к-во израсходанного какао) должно быть меньше либо равно запасу сырья для задач поиска максимальной прибыли. Нажимая на кнопку Добавить вводим все ограничения Добавить на сырье и на готовую продукцию.
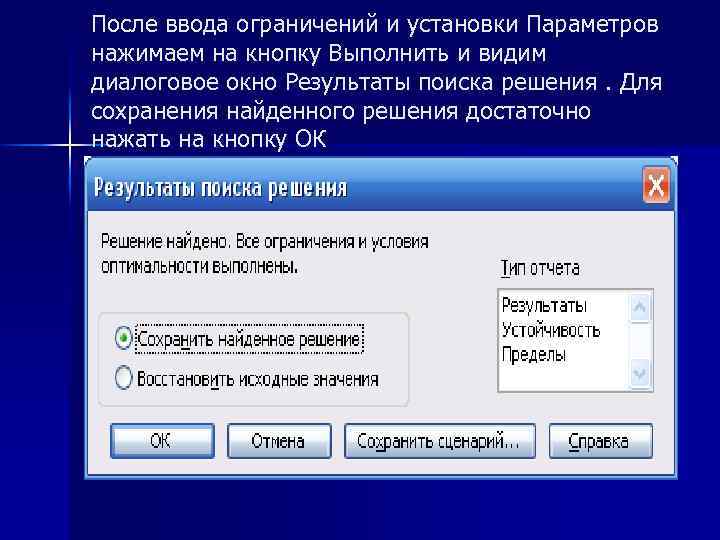
После ввода ограничений и установки Параметров нажимаем на кнопку Выполнить и видим диалоговое окно Результаты поиска решения. Для сохранения найденного решения достаточно нажать на кнопку ОК

Если все сделано верно, то решение будет таким, как на рисунке. Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет "В" и 20 кг конфет "С". Конфеты "А" производить не стоит. Полученная прибыль составит 400 $.

Математическая модель задачи Пусть: х1 -количество изделий А х2 -количество изделий В х3 -количество изделий С Тогда прибыль производства изделий можно выразить функцией: F(x)=9 х1+10 х2+16 х3 max

Задача найти максимум целевой функция F(x)=9 х1+10 х2+16 х3 При следующих ограничениях: 18 х1 +15 х2 +12 х3 <=360 6 х1 +4 х2 +8 х3 <=192 5 х1 +3 х2 +3 х3 <=180 х1 >=0 х2 >=0 х3 >=0
ПОИСК РЕШЕНИЯ-правильная.ppt