7856d2994787980c84b58c49483ddcbf.ppt
- Количество слайдов: 32

Tables & Graphs

Outline 1. Tables as representations of data 2. Graphs * * Definition Components 3. Types of graph * * Bar Line Frequency distribution Scattergram

Tables present data ¢ ¢ summarize data (no need to look at each individual data point). show numerical relationships in a matrix. ¢ advantage – effect sizes computable ¢ disadvantage – patterns in data more difficult to see than with graphs
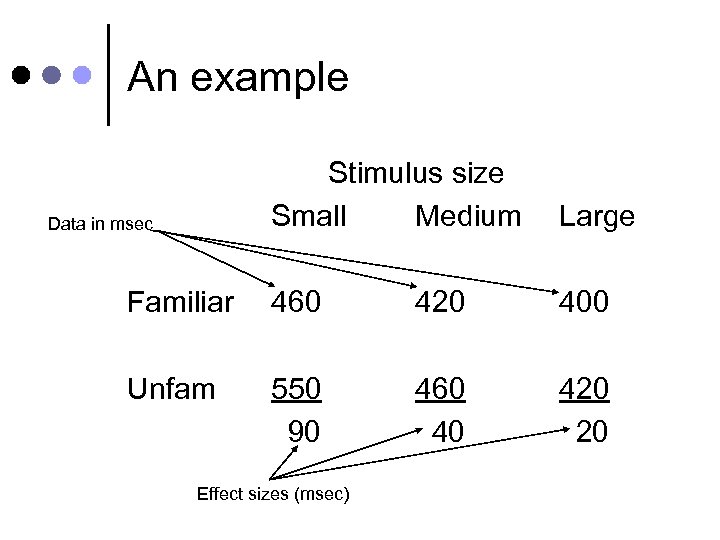
An example Stimulus size Small Medium Large Familiar 460 420 400 Unfam 550 90 460 40 420 20 Data in msec Effect sizes (msec)

2. Graphs – Definitions ¢ Graphs are visual representations of a set of data points. ¢ Most graphs are twodimensional, using Cartesian co-ordinate system (X and Y). ¢ Data are represented as a function relating X to Y.

2. Graphs – Components ¢ ¢ X (horizontal) axis = independent variable. Y (vertical) axis = dependent variable Y X
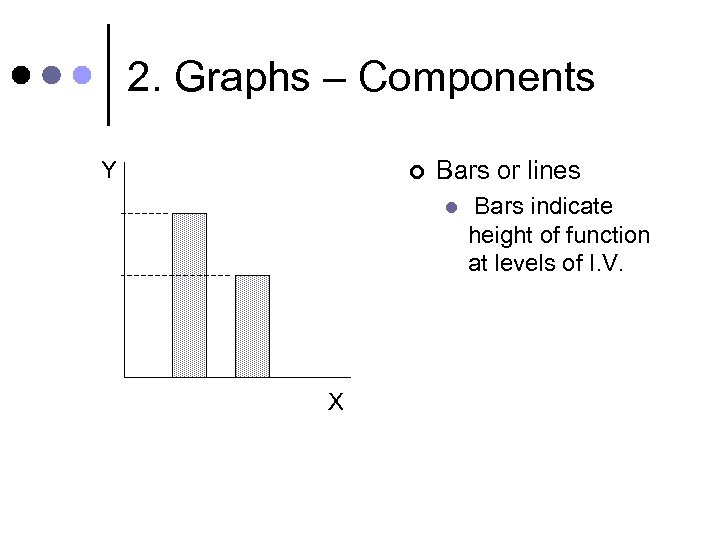
2. Graphs – Components Y ¢ Bars or lines l X Bars indicate height of function at levels of I. V.
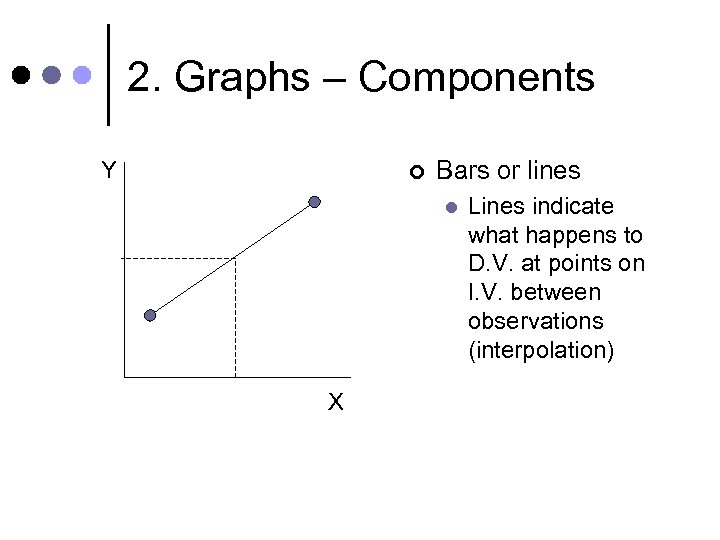
2. Graphs – Components Y ¢ Bars or lines l X Lines indicate what happens to D. V. at points on I. V. between observations (interpolation)

3. Types of graphs A. Bar graphs. B. Line graphs C. Frequency distributions D. Scattergrams

3 a – Bar Graphs ¢ Bar graphs Data represented as bars l height indicates D. V. l location along X axis indicates I. V. l Use when data are categorical rather than quantitative. l ¢ Example on next slide.
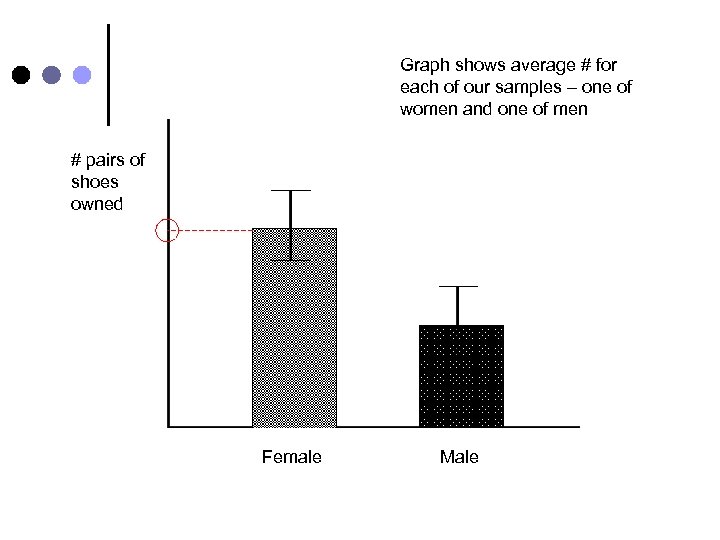
Graph shows average # for each of our samples – one of women and one of men # pairs of shoes owned Female Male

3 b – Line graphs ¢ ¢ ¢ Show D. V. as a function of I. V. Points show actual data Lines connecting points show interpolations ¢ Use when response varies continuously with I. V. – but be careful about interpolation and extrapolation.

3 b – Line Graphs ¢ Spatial relationships illustrate quantitative relationships Slope l Y-intercept l

3 b – Line Graphs ¢ Note the equation for a line: Y = ax + b a = slope and b = intercept.

Slope ¢ the rate of change in X with change in Y (or vice-versa). ¢ ¢ tells us how much change on Y scale is associated with a one-unit change on X slope can be positive or negative
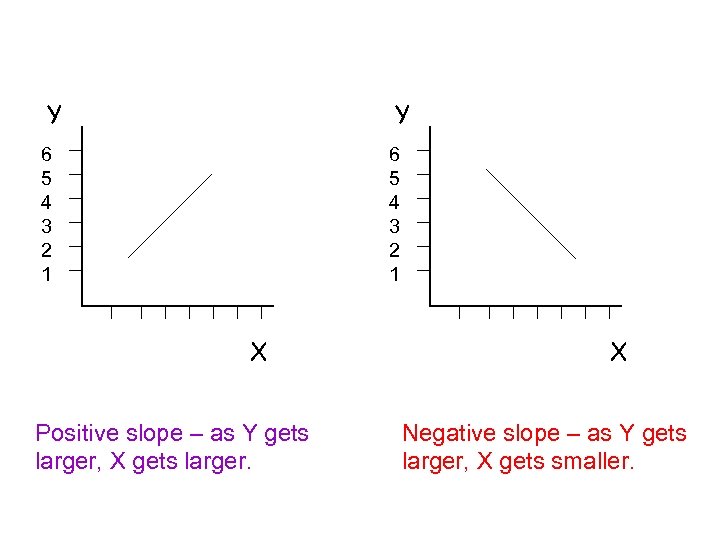
Y Y 6 5 4 3 2 1 X Positive slope – as Y gets larger, X gets larger. X Negative slope – as Y gets larger, X gets smaller.
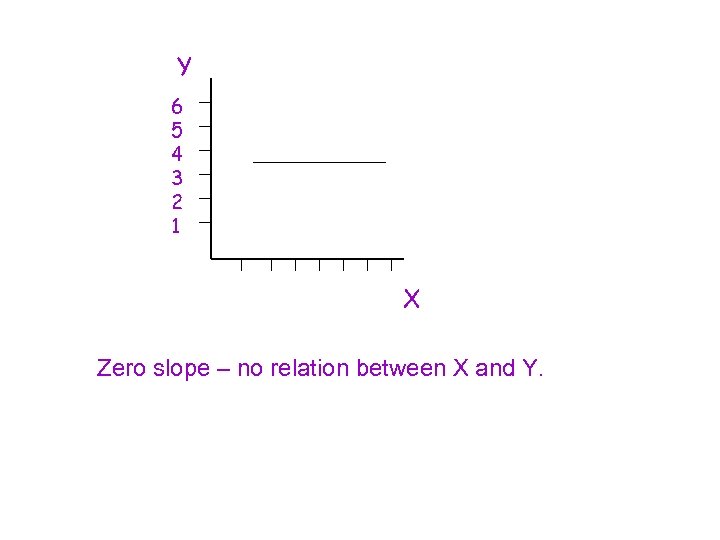
Y 6 5 4 3 2 1 X Zero slope – no relation between X and Y.

Intercept ¢ the value of Y when X = 0, so that the line intercepts the Y axis. ¢ shows minimum (or maximum) value of Y
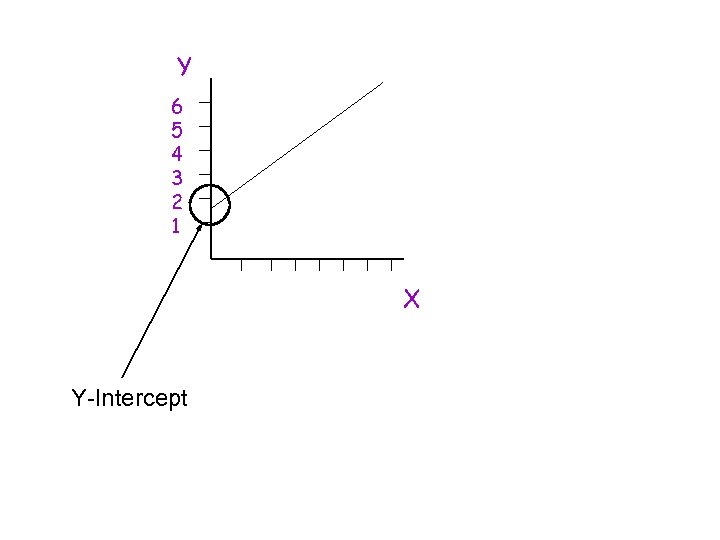
Y 6 5 4 3 2 1 X Y-Intercept
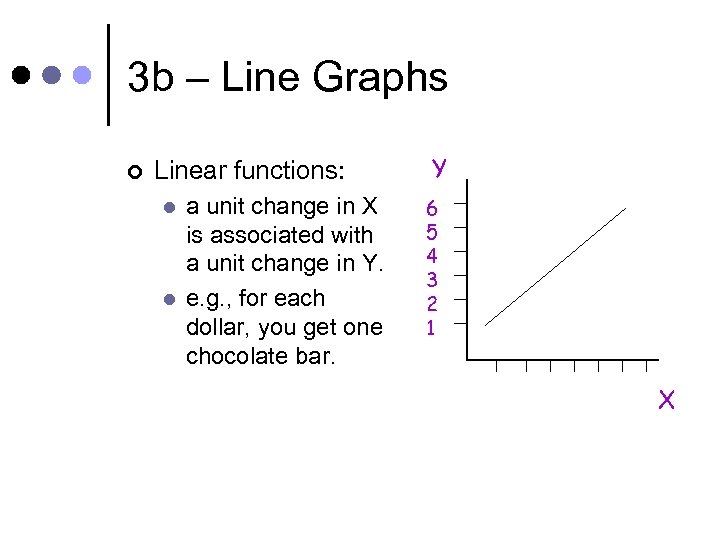
3 b – Line Graphs ¢ Linear functions: l l a unit change in X is associated with a unit change in Y. e. g. , for each dollar, you get one chocolate bar. Y 6 5 4 3 2 1 X

3 b – Line Graphs ¢ Non-linear functions: l l amount of change in Y for a unit change in X depends upon where you are on X scale. e. g. , the more chocolate bars you buy, the less each one costs.
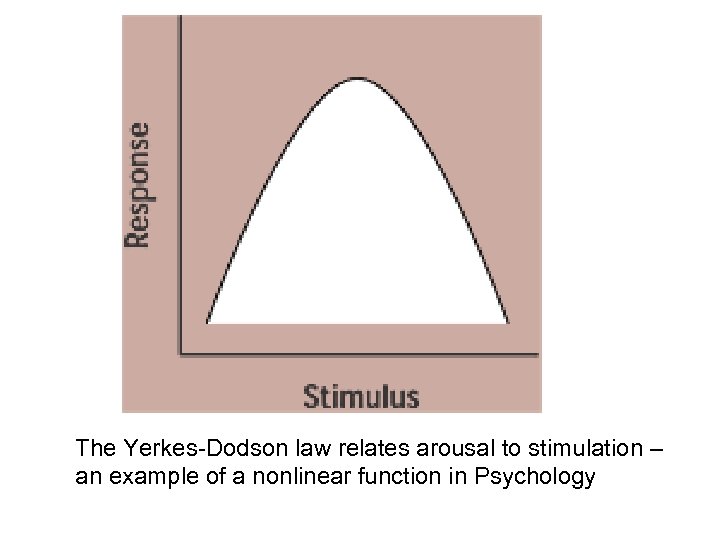
The Yerkes-Dodson law relates arousal to stimulation – an example of a nonlinear function in Psychology

3 c – Frequency Distributions ¢ Show frequency with which different observations happen ¢ Y axis = how many scores there at each X value in the data set.

3 c. Frequency distributions ¢ Show many scores occur in various ranges Range # of scores 1– 3 4– 6 7– 9 10 – 12 13 – 15 5 8 12 9 4
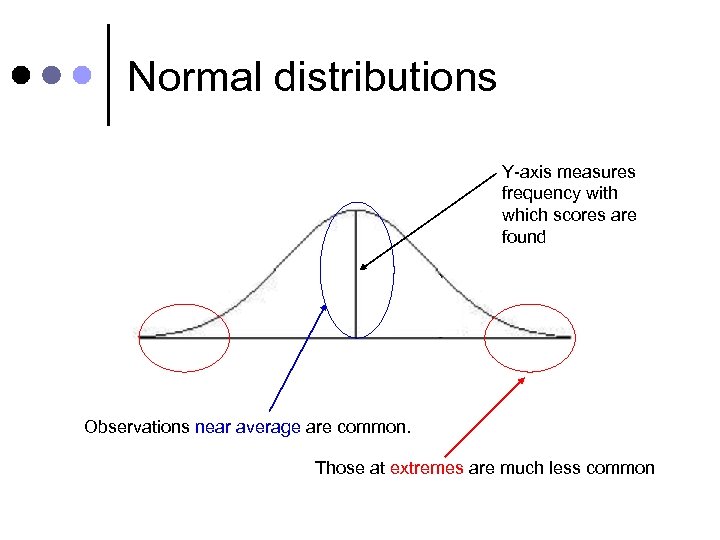
Normal distributions Y-axis measures frequency with which scores are found Observations near average are common. Those at extremes are much less common

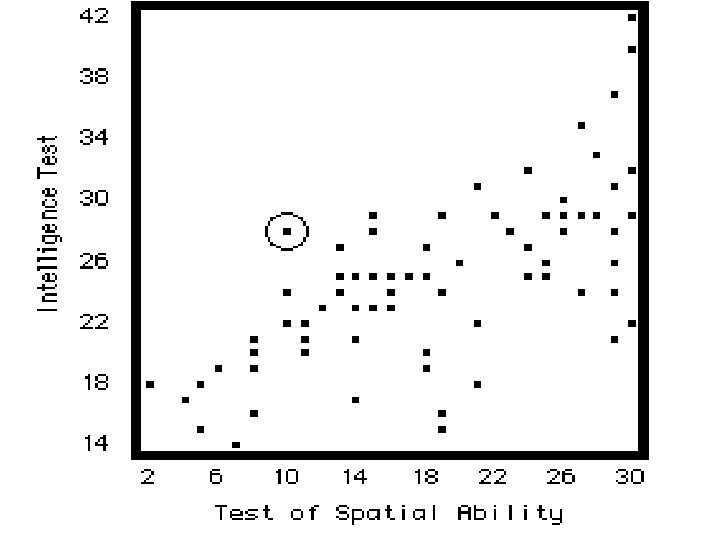
3 d - Scattergrams ¢ Show X-Y relation for individual cases ¢ That is, these show I. V. – D. V. relation for cases ¢ E. g. , on next slide, we see relationship between IQ (Y axis) and spatial ability (X axis)

3 e Importance of Tables and Graphs ¢ A good graph or table helps you understand your results. ¢ Similarly, a good graph or table helps you explain your results to someone else. ¢ Consider the following three ways of presenting roughly the same information:

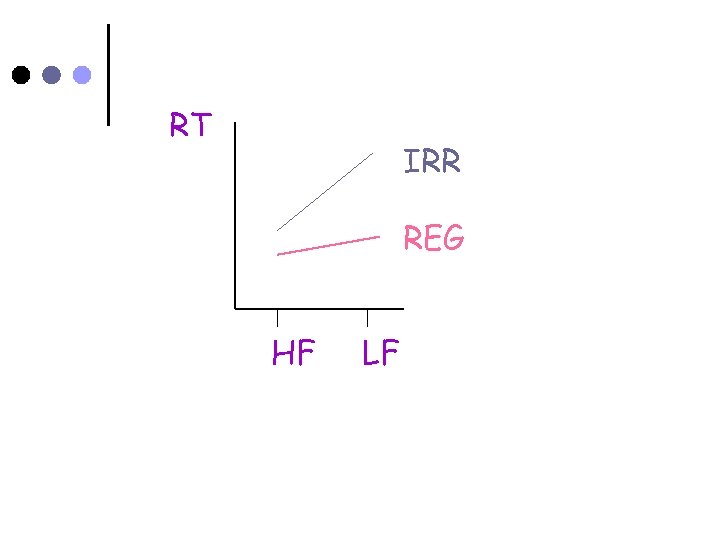
“High frequency words are read faster than low frequency words, but the difference is greater if the words are irregular in spelling than if they are regular in spelling. ”

Typical average reading times (msec) HF IRR REG LF 475 450 25 600 500 100 IRR = irregularly spelled words REG = regularly spelled words 125 50 HF = high frequency LF = low frequency
RT IRR REG HF LF

Review ¢ Tables and graphs summarize data ¢ ¢ Graphs use spatial relationships to show relationships among variables in the data Tables allow quick computation of effect sizes ¢ Graphs show patterns in the data
7856d2994787980c84b58c49483ddcbf.ppt