6a35289d94687f4a9884b9687cfa3bb8.ppt
- Количество слайдов: 80

Table of Contents CD Chapter 16 (PERT/CPM Models for Project Management) A Case Study: The Reliable Construction Co. Project (Section 16. 1) Using a Network to Visually Display a Project (Section 16. 2) Scheduling a Project with PERT/CPM (Section 16. 3) Dealing with Uncertain Activity Durations (Section 16. 4) Considering Time-Cost Tradeoffs (Section 16. 5) Scheduling and Controlling Project Costs (Section 16. 6) 16. 2– 16. 3 16. 4– 16. 7 16. 8– 16. 17 16. 18– 16. 26 16. 27– 16. 38 16. 39– 16. 46 Introduction to Project Management (UW Lecture) 16. 47– 16. 57 These slides are based upon a lecture from the course “Principles of Operations Management”, (an undergraduate business class) at the University of Washington (as taught by one of the authors). Project Management with Uncertain Activity Durations (UW Lecture) 16. 58– 16. 69 These slides are based upon a lecture from the course “Principles of Operations Management” (an undergraduate business class) at the University of Washington (as taught by one of the authors). Time-Cost Tradeoffs (UW Lecture) 16. 70– 16. 81 These slides are based upon a lecture from the course “Principles of Operations Management” (an undergraduate business class) at the University of Washington (as taught by one of the authors). Mc. Graw-Hill/Irwin 16. 1 © The Mc. Graw-Hill Companies, Inc. , 2008

Reliable Construction Company Project • The Reliable Construction Company has just made the winning bid of $5. 4 million to construct a new plant for a major manufacturer. • The contract includes the following provisions: – A penalty of $300, 000 if Reliable has not completed construction within 47 weeks. – A bonus of $150, 000 if Reliable has completed the plant within 40 weeks. Questions: 1. 2. 3. 4. 5. 6. 7. 8. How can the project be displayed graphically to better visualize the activities? What is the total time required to complete the project if no delays occur? When do the individual activities need to start and finish? What are the critical bottleneck activities? For other activities, how much delay can be tolerated? What is the probability the project can be completed in 47 weeks? What is the least expensive way to complete the project within 40 weeks? How should ongoing costs be monitored to try to keep the project within budget? Mc. Graw-Hill/Irwin 16. 2 © The Mc. Graw-Hill Companies, Inc. , 2008
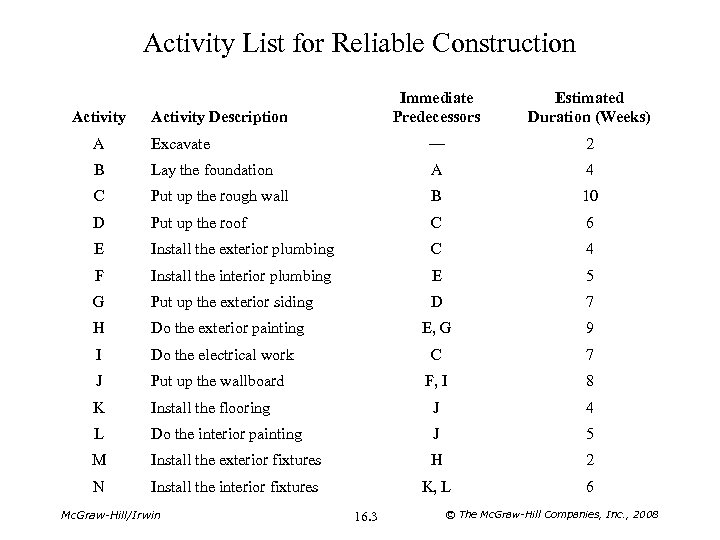
Activity List for Reliable Construction Activity Immediate Predecessors Activity Description Estimated Duration (Weeks) A Excavate — 2 B Lay the foundation A 4 C Put up the rough wall B 10 D Put up the roof C 6 E Install the exterior plumbing C 4 F Install the interior plumbing E 5 G Put up the exterior siding D 7 H Do the exterior painting E, G 9 I Do the electrical work C 7 J Put up the wallboard F, I 8 K Install the flooring J 4 L Do the interior painting J 5 M Install the exterior fixtures H 2 N Install the interior fixtures K, L 6 Mc. Graw-Hill/Irwin 16. 3 © The Mc. Graw-Hill Companies, Inc. , 2008

Project Networks • A network used to represent a project is called a project network. • A project network consists of a number of nodes and a number of arcs. • Two types of project networks: – Activity-on-arc (AOA): each activity is represented by an arc. A node is used to separate an activity from its predecessors. The sequencing of the arcs shows the precedence relationships. – Activity-on-node (AON): each activity is represented by a node. The arcs are used to show the precedence relationships. • Advantages of AON (used in this textbook): – considerably easier to construct – easier to understand – easier to revise when there are changes Mc. Graw-Hill/Irwin 16. 4 © The Mc. Graw-Hill Companies, Inc. , 2008
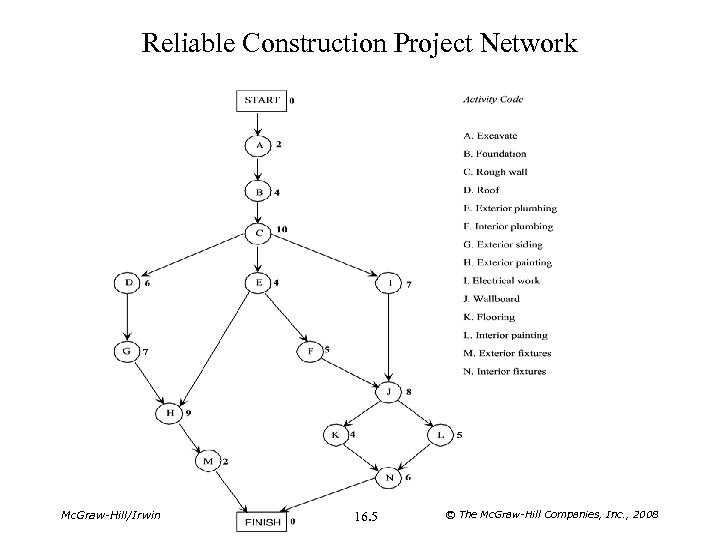
Reliable Construction Project Network Mc. Graw-Hill/Irwin 16. 5 © The Mc. Graw-Hill Companies, Inc. , 2008
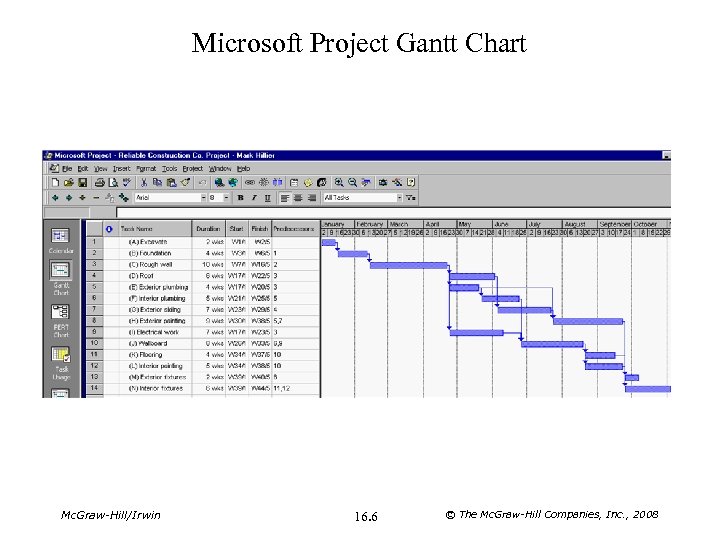
Microsoft Project Gantt Chart Mc. Graw-Hill/Irwin 16. 6 © The Mc. Graw-Hill Companies, Inc. , 2008
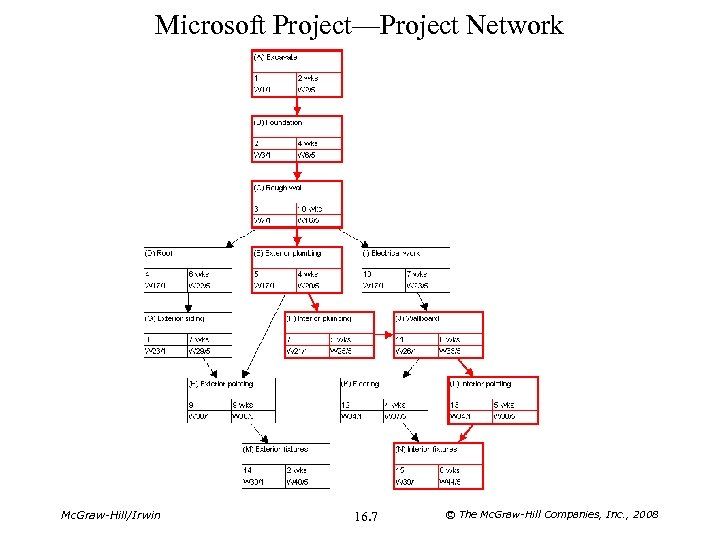
Microsoft Project—Project Network Mc. Graw-Hill/Irwin 16. 7 © The Mc. Graw-Hill Companies, Inc. , 2008

The Critical Path • A path through a network is one of the routes following the arrows (arcs) from the start node to the finish node. • The length of a path is the sum of the (estimated) durations of the activities on the path. • The (estimated) project duration equals the length of the longest path through the project network. • This longest path is called the critical path. (If more than one path tie for the longest, they all are critical paths. ) Mc. Graw-Hill/Irwin 16. 8 © The Mc. Graw-Hill Companies, Inc. , 2008

The Paths for Reliable’s Project Network Path Length (Weeks) Start A B C D G H M Finish 2 + 4 + 10 + 6 + 7 + 9 + 2 = 40 Start A B C E H M Finish 2 + 4 + 10 + 4 + 9 + 2 = 31 Start A B C E F J K N Finish 2 + 4 + 10 + 4 + 5 + 8 + 4 + 6 = 43 Start A B C E F J L N Finish 2 + 4 + 10 + 4 + 5 + 8 + 5 + 6 = 44 Start A B C I J K N Finish 2 + 4 + 10 + 7 + 8 + 4 + 6 = 41 Start A B C I J L N Finish 2 + 4 + 10 + 7 + 8 + 5 + 6 = 42 Mc. Graw-Hill/Irwin 16. 9 © The Mc. Graw-Hill Companies, Inc. , 2008

Earliest Start and Earliest Finish Times • The starting and finishing times of each activity if no delays occur anywhere in the project are called the earliest start time and the earliest finish time. – ES = Earliest start time for a particular activity – EF = Earliest finish time for a particular activity • Earliest Start Time Rule: ES = Largest EF of the immediate predecessors. • Procedure for obtaining earliest times for all activities: 1. For each activity that starts the project (including the start node), set its ES = 0. 2. For each activity whose ES has just been obtained, calculate EF = ES + duration. 3. For each new activity whose immediate predecessors now have EF values, obtain its ES by applying the earliest start time rule. Apply step 2 to calculate EF. 4. Repeat step 3 until ES and EF have been obtained for all activities. Mc. Graw-Hill/Irwin 16. 10 © The Mc. Graw-Hill Companies, Inc. , 2008
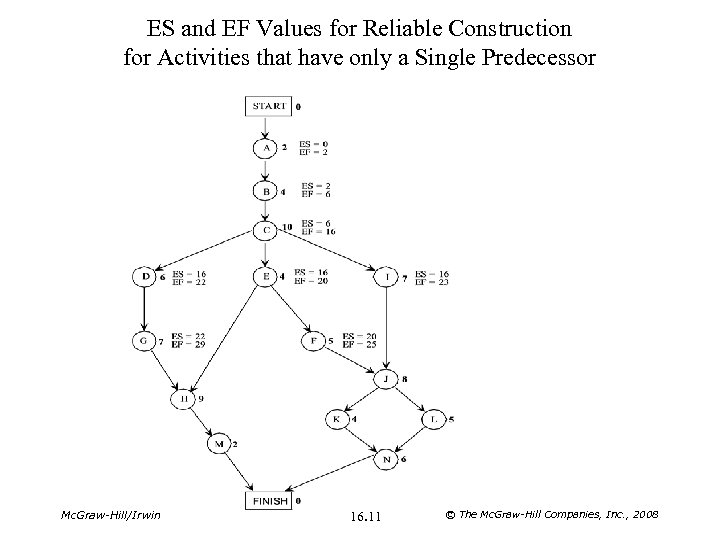
ES and EF Values for Reliable Construction for Activities that have only a Single Predecessor Mc. Graw-Hill/Irwin 16. 11 © The Mc. Graw-Hill Companies, Inc. , 2008
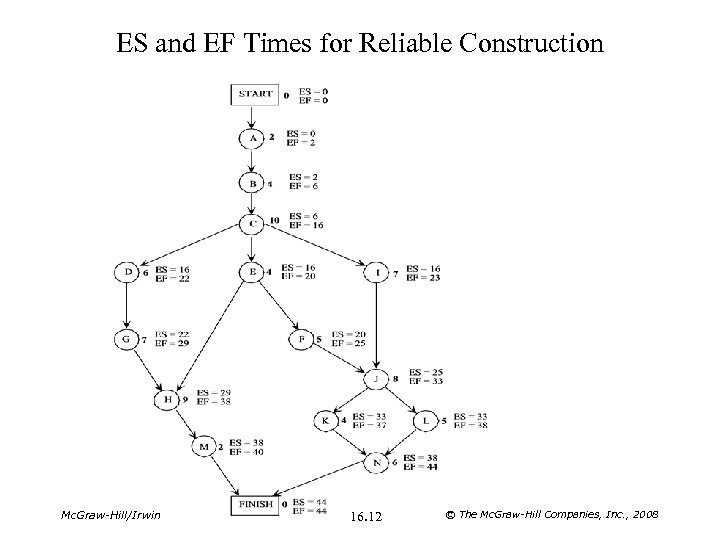
ES and EF Times for Reliable Construction Mc. Graw-Hill/Irwin 16. 12 © The Mc. Graw-Hill Companies, Inc. , 2008

Latest Start and Latest Finish Times • The latest start time for an activity is the latest possible time that it can start without delaying the completion of the project (so the finish node still is reached at its earliest finish time). The latest finish time has the corresponding definition with respect to finishing the activity. – LS = Latest start time for a particular activity – LF = Latest finish time for a particular activity • Latest Finish Time Rule: LF = Smallest LS of the immediate successors. • Procedure for obtaining latest times for all activities: 1. For each of the activities that together complete the project (including the finish node), set LF equal to EF of the finish node. 2. For each activity whose LF value has just been obtained, calculate LS = LF – duration. 3. For each new activity whose immediate successors now have LS values, obtain its LF by applying the latest finish time rule. Apply step 2 to calculate its LS. 4. Repeat step 3 until LF and LS have been obtained for all activities. Mc. Graw-Hill/Irwin 16. 13 © The Mc. Graw-Hill Companies, Inc. , 2008
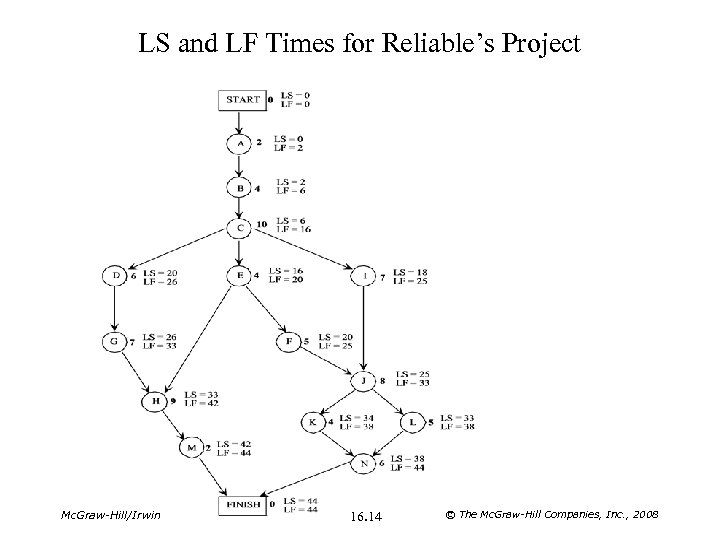
LS and LF Times for Reliable’s Project Mc. Graw-Hill/Irwin 16. 14 © The Mc. Graw-Hill Companies, Inc. , 2008
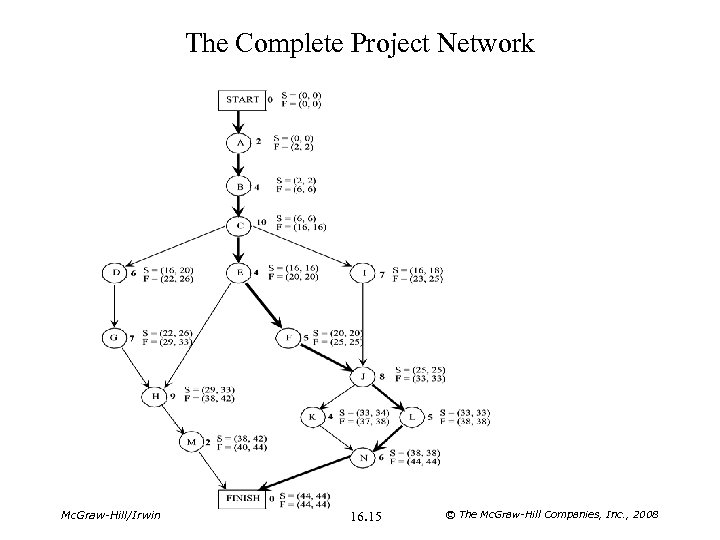
The Complete Project Network Mc. Graw-Hill/Irwin 16. 15 © The Mc. Graw-Hill Companies, Inc. , 2008
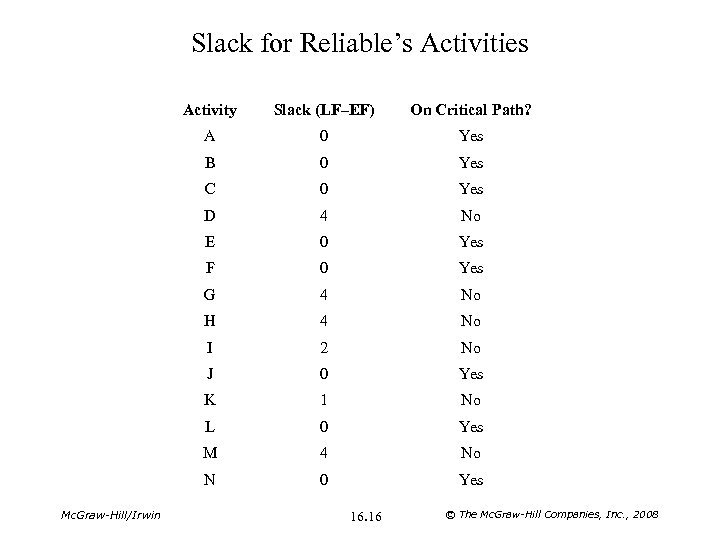
Slack for Reliable’s Activities Activity On Critical Path? A 0 Yes B 0 Yes C 0 Yes D 4 No E 0 Yes F 0 Yes G 4 No H 4 No I 2 No J 0 Yes K 1 No L 0 Yes M 4 No N Mc. Graw-Hill/Irwin Slack (LF–EF) 0 Yes 16. 16 © The Mc. Graw-Hill Companies, Inc. , 2008
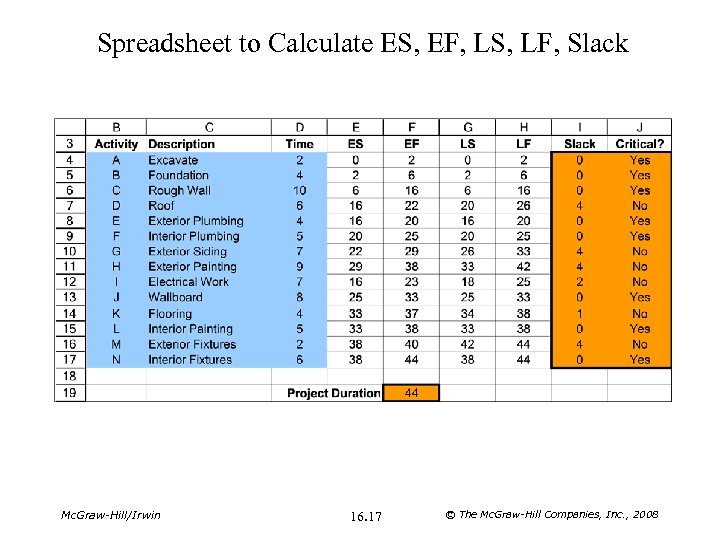
Spreadsheet to Calculate ES, EF, LS, LF, Slack Mc. Graw-Hill/Irwin 16. 17 © The Mc. Graw-Hill Companies, Inc. , 2008
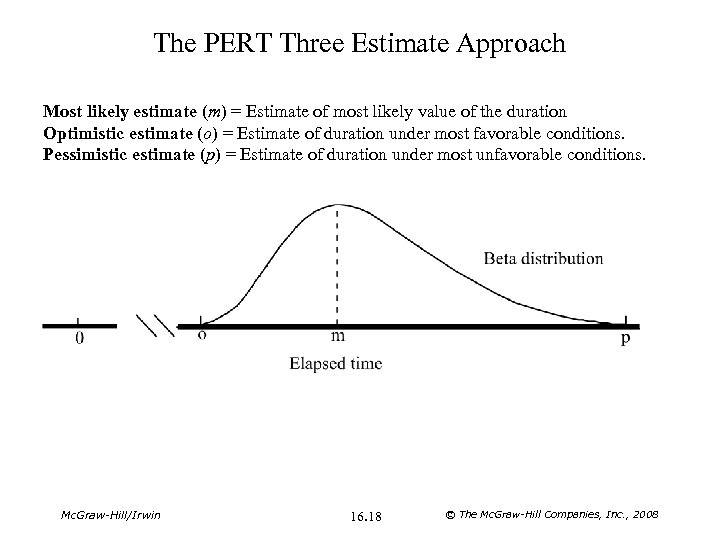
The PERT Three Estimate Approach Most likely estimate (m) = Estimate of most likely value of the duration Optimistic estimate (o) = Estimate of duration under most favorable conditions. Pessimistic estimate (p) = Estimate of duration under most unfavorable conditions. Mc. Graw-Hill/Irwin 16. 18 © The Mc. Graw-Hill Companies, Inc. , 2008

Mean and Standard Deviation An approximate formula for the variance ( 2) of an activity is An approximate formula for the mean (m) of an activity is Mc. Graw-Hill/Irwin 16. 19 © The Mc. Graw-Hill Companies, Inc. , 2008
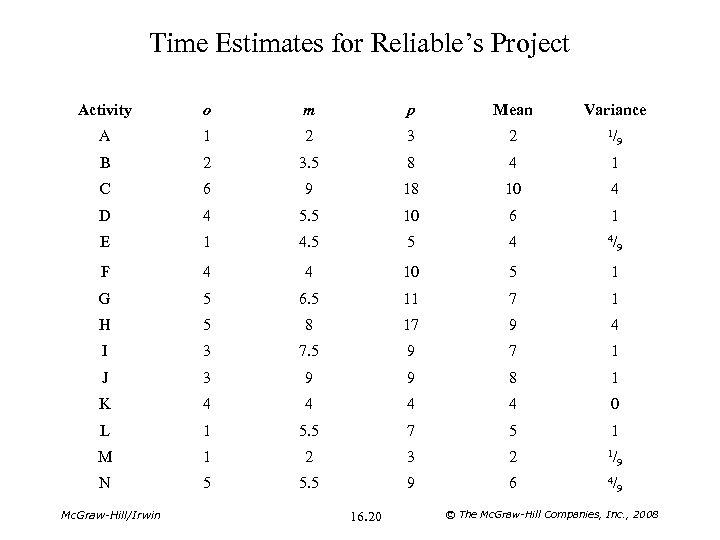
Time Estimates for Reliable’s Project Activity o m p Mean Variance A 1 2 3 2 1/ B 2 3. 5 8 4 1 C 6 9 18 10 4 D 4 5. 5 10 6 1 E 1 4. 5 5 4 4/ F 4 4 10 5 1 G 5 6. 5 11 7 1 H 5 8 17 9 4 I 3 7. 5 9 7 1 J 3 9 9 8 1 K 4 4 0 L 1 5. 5 7 5 1 M 1 2 3 2 1/ 9 N 5 5. 5 9 6 4/ 9 Mc. Graw-Hill/Irwin 16. 20 9 9 © The Mc. Graw-Hill Companies, Inc. , 2008

Pessimistic Path Lengths for Reliable’s Project Path Pessimistic Length (Weeks) Start A B C D G H M Finish 3 + 8 + 10 + 11 + 17 + 3 = 70 Start A B C E H M Finish 3 + 8 + 18 + 5 + 17 + 3 = 54 Start A B C E F J K N Finish 3 + 8 + 18 + 5 + 10 + 9 + 4 + 9 = 66 Start A B C E F J L N Finish 3 + 8 + 18 + 5 + 10 + 9 + 7 + 9 = 69 Start A B C I J K N Finish 3 + 8 + 18 + 9 + 4 + 9 = 60 Start A B C I J L N Finish 3 + 8 + 18 + 9 + 7 + 9 = 63 Mc. Graw-Hill/Irwin 16. 21 © The Mc. Graw-Hill Companies, Inc. , 2008

Three Simplifying Approximations of PERT/CPM 1. The mean critical path will turn out to be the longest path through the project network. 2. The durations of the activities on the mean critical path are statistically independent. Thus, the three estimates of the duration of an activity would never change after learning the durations of some of the other activities. 3. The form of the probability distribution of project duration is the normal distribution. By using simplifying approximations 1 and 2, there is some statistical theory (one version of the central limit theorem) that justifies this as being a reasonable approximation if the number of activities on the mean critical path is not too small. Mc. Graw-Hill/Irwin 16. 22 © The Mc. Graw-Hill Companies, Inc. , 2008
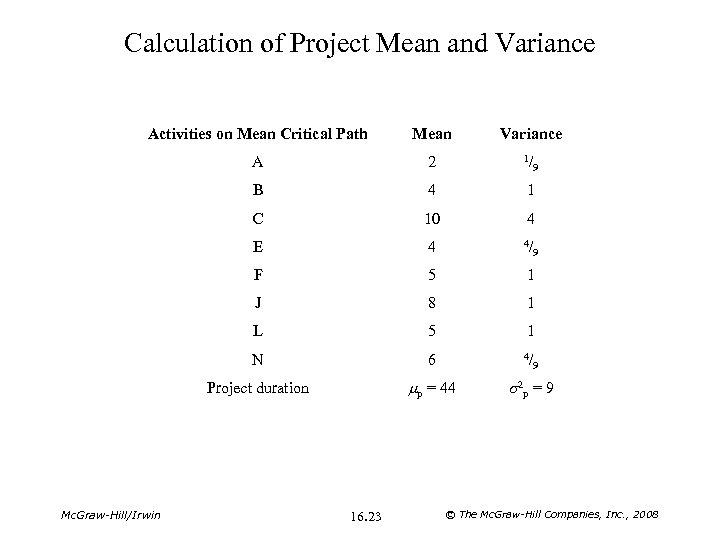
Calculation of Project Mean and Variance Activities on Mean Critical Path Mean Variance A 2 1/ B 4 1 C 10 4 E 4 4/ F 5 1 J 8 1 L 5 1 N 6 4/ Project duration mp = 44 s 2 p = 9 Mc. Graw-Hill/Irwin 16. 23 9 9 9 © The Mc. Graw-Hill Companies, Inc. , 2008
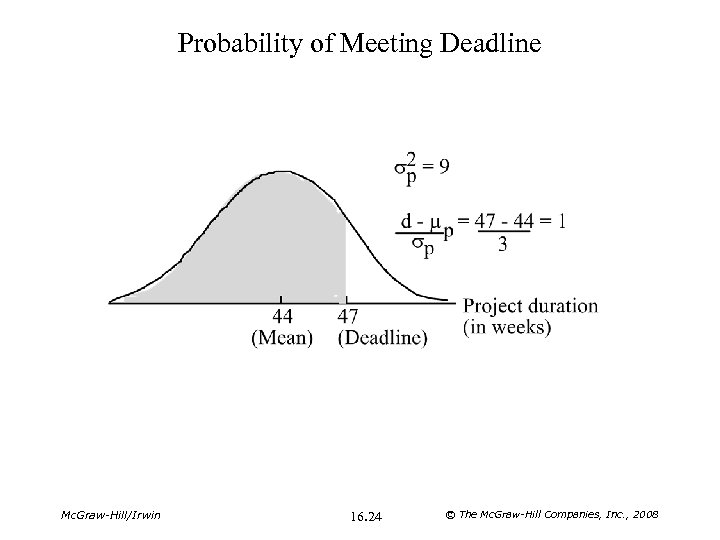
Probability of Meeting Deadline Mc. Graw-Hill/Irwin 16. 24 © The Mc. Graw-Hill Companies, Inc. , 2008
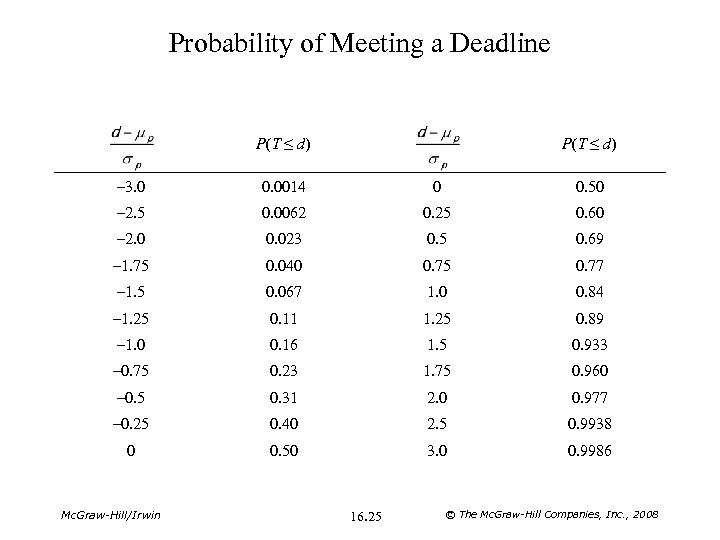
Probability of Meeting a Deadline P(T ≤ d) – 3. 0 0. 0014 0 0. 50 – 2. 5 0. 0062 0. 25 0. 60 – 2. 0 0. 023 0. 5 0. 69 – 1. 75 0. 040 0. 75 0. 77 – 1. 5 0. 067 1. 0 0. 84 – 1. 25 0. 11 1. 25 0. 89 – 1. 0 0. 16 1. 5 0. 933 – 0. 75 0. 23 1. 75 0. 960 – 0. 5 0. 31 2. 0 0. 977 – 0. 25 0. 40 2. 5 0. 9938 0 0. 50 3. 0 0. 9986 Mc. Graw-Hill/Irwin 16. 25 © The Mc. Graw-Hill Companies, Inc. , 2008
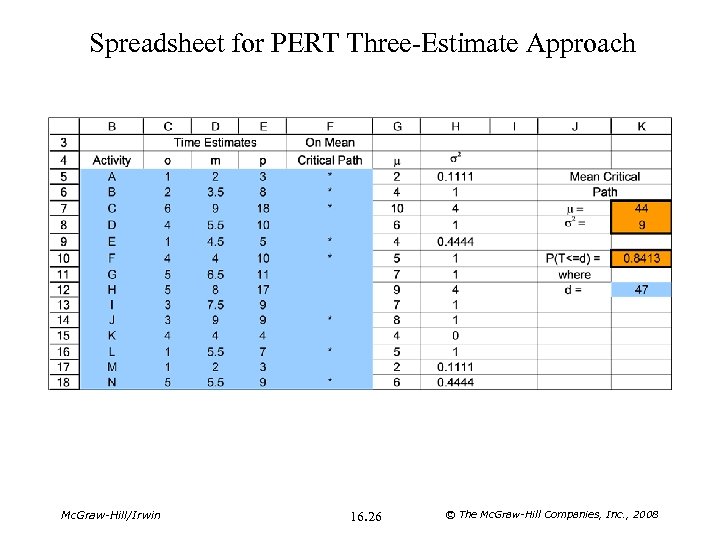
Spreadsheet for PERT Three-Estimate Approach Mc. Graw-Hill/Irwin 16. 26 © The Mc. Graw-Hill Companies, Inc. , 2008

Considering Time-Cost Trade-Offs Question: If extra money is spent to expedite the project, what is the least expensive way of attempting to meet the target completion time (40 weeks)? CPM Method of Time-Cost Trade-Offs: – Crashing an activity refers to taking special costly measures to reduce the duration of an activity below its normal value. Special measures might include overtime, hiring additional temporary help, using special time-saving materials, obtaining special equipment, etc. – Crashing the project refers to crashing a number of activities to reduce the duration of the project below its normal value. Mc. Graw-Hill/Irwin 16. 27 © The Mc. Graw-Hill Companies, Inc. , 2008
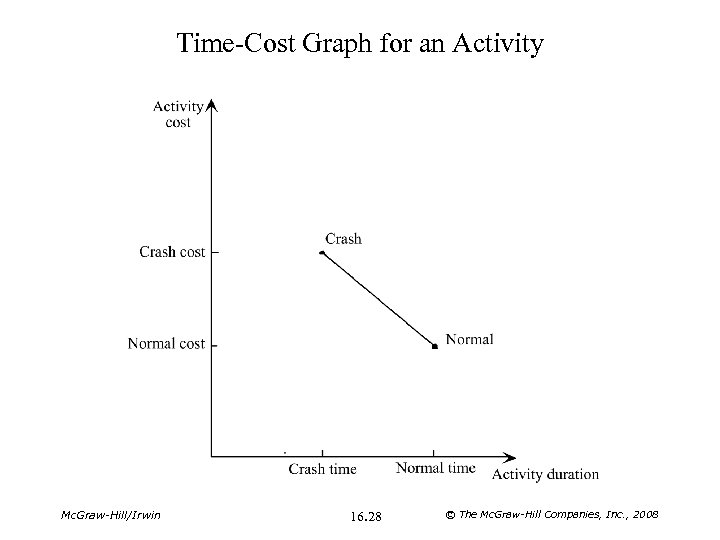
Time-Cost Graph for an Activity Mc. Graw-Hill/Irwin 16. 28 © The Mc. Graw-Hill Companies, Inc. , 2008
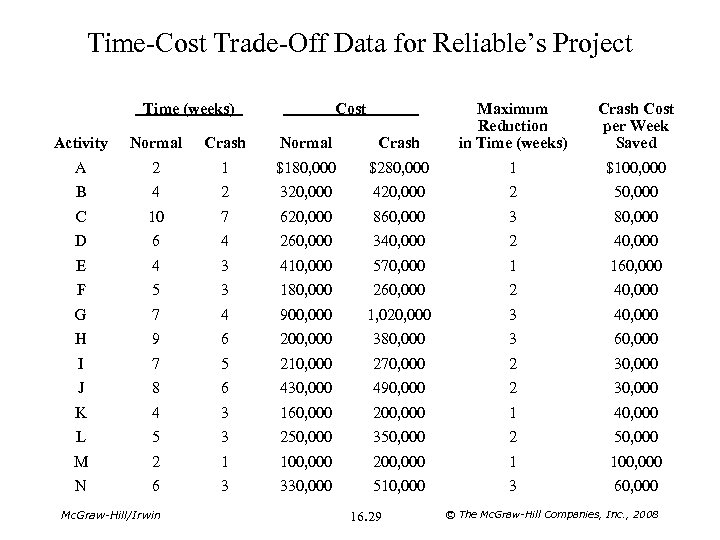
Time-Cost Trade-Off Data for Reliable’s Project Activity Normal Crash Maximum Reduction in Time (weeks) A 2 1 $180, 000 $280, 000 1 $100, 000 B 4 2 320, 000 420, 000 2 50, 000 C 10 7 620, 000 860, 000 3 80, 000 D 6 4 260, 000 340, 000 2 40, 000 E 4 3 410, 000 570, 000 1 160, 000 F 5 3 180, 000 260, 000 2 40, 000 G 7 4 900, 000 1, 020, 000 3 40, 000 H 9 6 200, 000 380, 000 3 60, 000 I 7 5 210, 000 270, 000 2 30, 000 J 8 6 430, 000 490, 000 2 30, 000 K 4 3 160, 000 200, 000 1 40, 000 L 5 3 250, 000 350, 000 2 50, 000 M 2 1 100, 000 200, 000 1 100, 000 N 6 3 330, 000 510, 000 3 60, 000 Time (weeks) Mc. Graw-Hill/Irwin Cost 16. 29 Crash Cost per Week Saved © The Mc. Graw-Hill Companies, Inc. , 2008
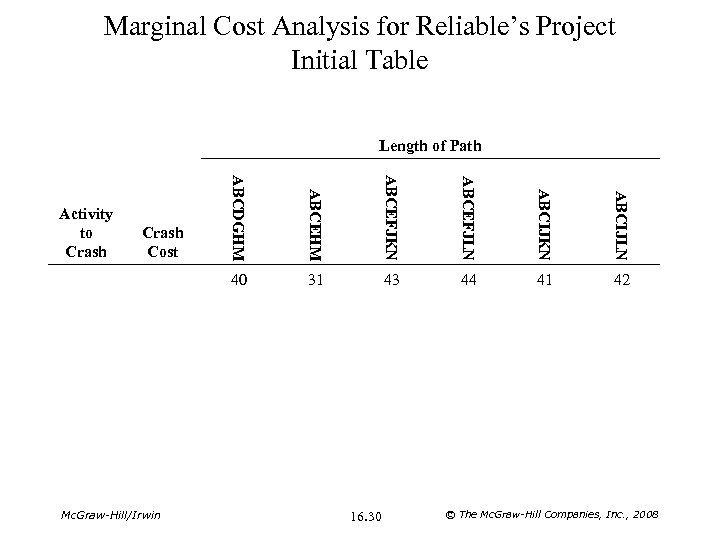
Marginal Cost Analysis for Reliable’s Project Initial Table Length of Path ABCEFJKN ABCEFJLN ABCIJKN ABCIJLN Mc. Graw-Hill/Irwin ABCEHM Crash Cost ABCDGHM 40 Activity to Crash 31 43 44 41 42 16. 30 © The Mc. Graw-Hill Companies, Inc. , 2008
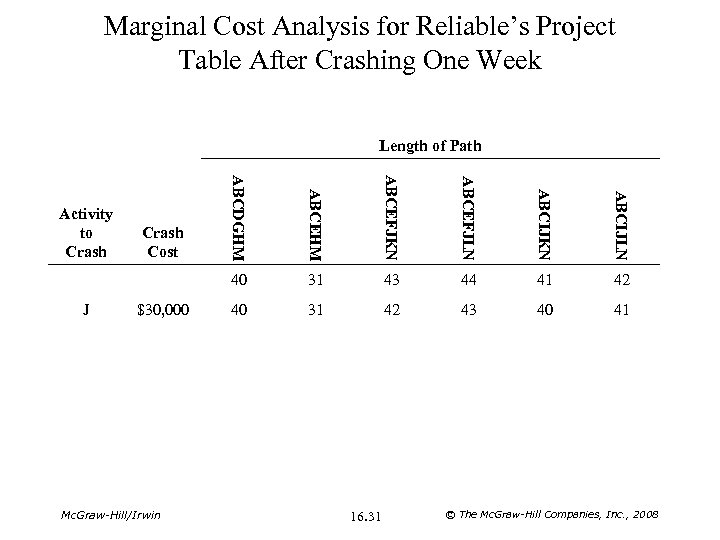
Marginal Cost Analysis for Reliable’s Project Table After Crashing One Week Length of Path ABCEFJLN ABCIJKN ABCIJLN Mc. Graw-Hill/Irwin ABCEFJKN $30, 000 ABCEHM J Crash Cost ABCDGHM 40 Activity to Crash 31 43 44 41 42 40 31 42 43 40 41 16. 31 © The Mc. Graw-Hill Companies, Inc. , 2008
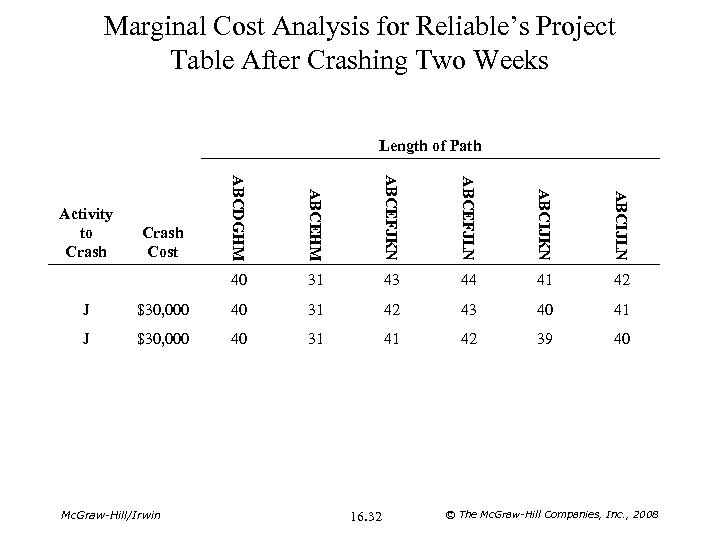
Marginal Cost Analysis for Reliable’s Project Table After Crashing Two Weeks Length of Path ABCEHM ABCEFJKN ABCEFJLN ABCIJKN ABCIJLN Crash Cost ABCDGHM 40 Activity to Crash 31 43 44 41 42 J $30, 000 40 31 42 43 40 41 J $30, 000 40 31 41 42 39 40 Mc. Graw-Hill/Irwin 16. 32 © The Mc. Graw-Hill Companies, Inc. , 2008
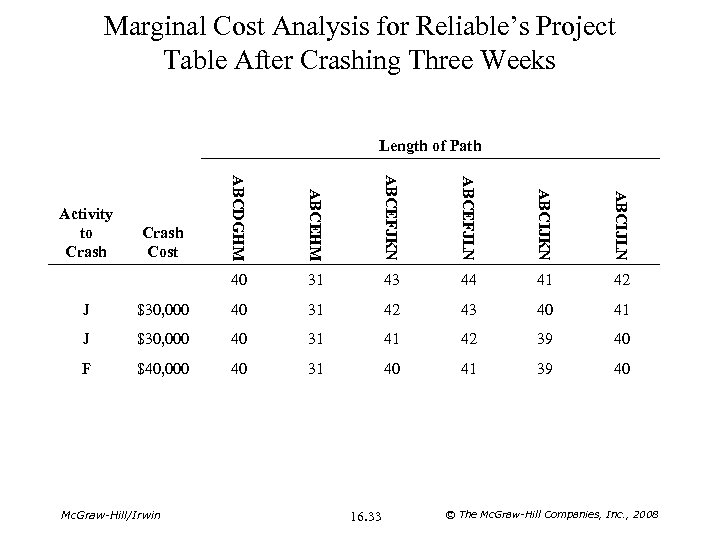
Marginal Cost Analysis for Reliable’s Project Table After Crashing Three Weeks Length of Path ABCEHM ABCEFJKN ABCEFJLN ABCIJKN ABCIJLN Crash Cost ABCDGHM 40 Activity to Crash 31 43 44 41 42 J $30, 000 40 31 42 43 40 41 J $30, 000 40 31 41 42 39 40 F $40, 000 40 31 40 41 39 40 Mc. Graw-Hill/Irwin 16. 33 © The Mc. Graw-Hill Companies, Inc. , 2008
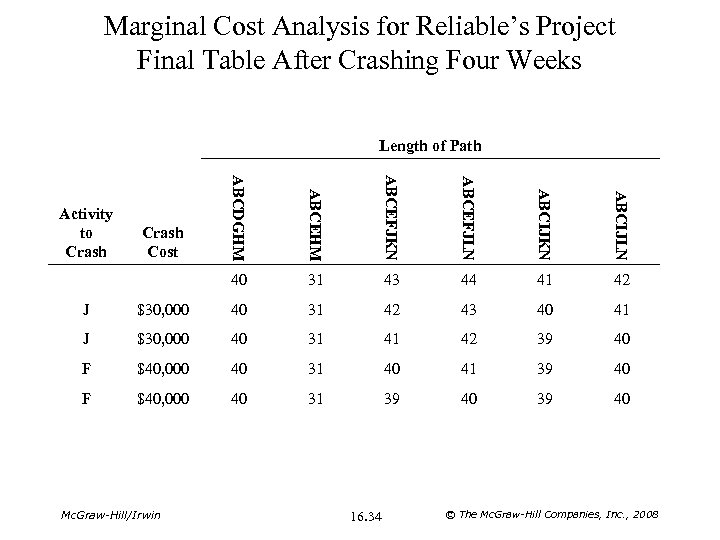
Marginal Cost Analysis for Reliable’s Project Final Table After Crashing Four Weeks Length of Path ABCEHM ABCEFJKN ABCEFJLN ABCIJKN ABCIJLN Crash Cost ABCDGHM 40 Activity to Crash 31 43 44 41 42 J $30, 000 40 31 42 43 40 41 J $30, 000 40 31 41 42 39 40 F $40, 000 40 31 40 41 39 40 F $40, 000 40 31 39 40 Mc. Graw-Hill/Irwin 16. 34 © The Mc. Graw-Hill Companies, Inc. , 2008
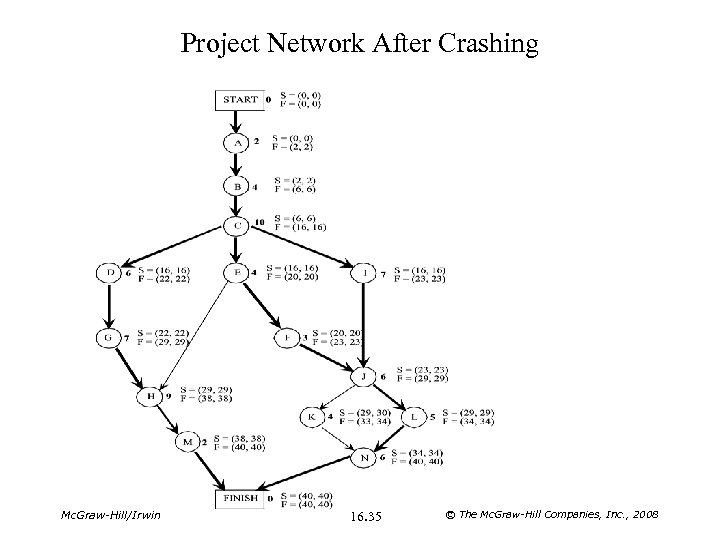
Project Network After Crashing Mc. Graw-Hill/Irwin 16. 35 © The Mc. Graw-Hill Companies, Inc. , 2008

Using LP to Make Crashing Decisions • Restatment of the problem: Consider the total cost of the project, including the extra cost of crashing activities. The problem then is to minimize this total cost, subject to the constraint that project duration must be less than or equal to the time desired by the project manager. • The decisions to be made are the following: 1. The start time of each activity. 2. The reduction in the duration of each activity due to crashing. 3. The finish time of the project (must not exceed 40 weeks). • The constraints are: 1. 2. 3. 4. Time Reduction ≤ Max Reduction (for each activity). Project Finish Time ≤ Desired Finish Time. Activity Start Time ≥ Activity Finish Time of all predecessors (for each activity). Project Finish Time ≥ Finish Time of all immediate predecessors of finish node. Mc. Graw-Hill/Irwin 16. 36 © The Mc. Graw-Hill Companies, Inc. , 2008
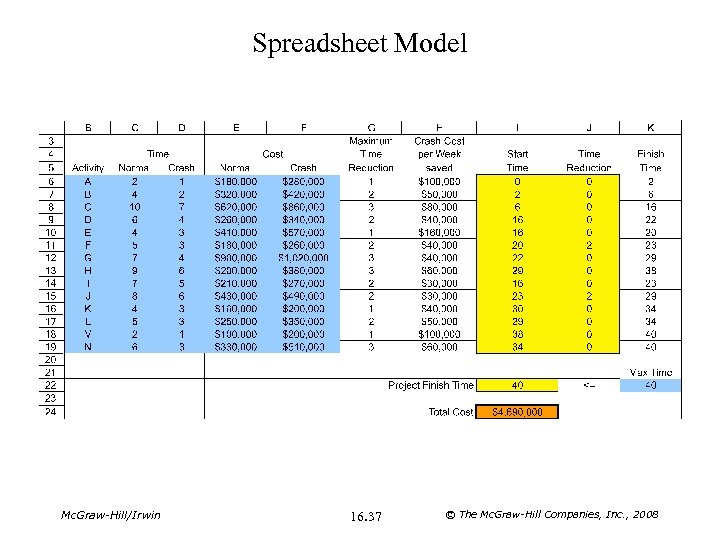
Spreadsheet Model Mc. Graw-Hill/Irwin 16. 37 © The Mc. Graw-Hill Companies, Inc. , 2008

Mr. Perty’s Conclusions • The plan for crashing the project only provides a 50 percent chance of actually finishing the project within 40 weeks, so the extra cost of the plan ($140, 000) is not justified. Therefore, Mr. Perty rejects any crashing at this stage. • The extra cost of the crashing plan can be justified if it almost certainly would earn the bonus of $150, 000 for finishing the project within 40 weeks. Therefore, Mr. Perty will hold the plan in reserve to be implemented if the project is running well ahead of schedule before reaching activity F. • The extra cost of part or all of the crashing plan can be easily justified if it likely would make the difference in avoiding the penalty of $300, 000 for not finishing the project within 47 weeks. Therefore, Mr. Perty will hold the crashing plan in reserve to be partially or wholly implemented if the project is running far behind schedule before reaching activity F or activity J. Mc. Graw-Hill/Irwin 16. 38 © The Mc. Graw-Hill Companies, Inc. , 2008

Scheduling and Controlling Project Costs • PERT/Cost is a systematic procedure (normally computerized) to help the project manager plan, schedule, and control costs. • Assumption: A common assumption when using PERT/Cost is that the costs of performing an activity are incurred at a constant rate throughout its duration. Mc. Graw-Hill/Irwin 16. 39 © The Mc. Graw-Hill Companies, Inc. , 2008
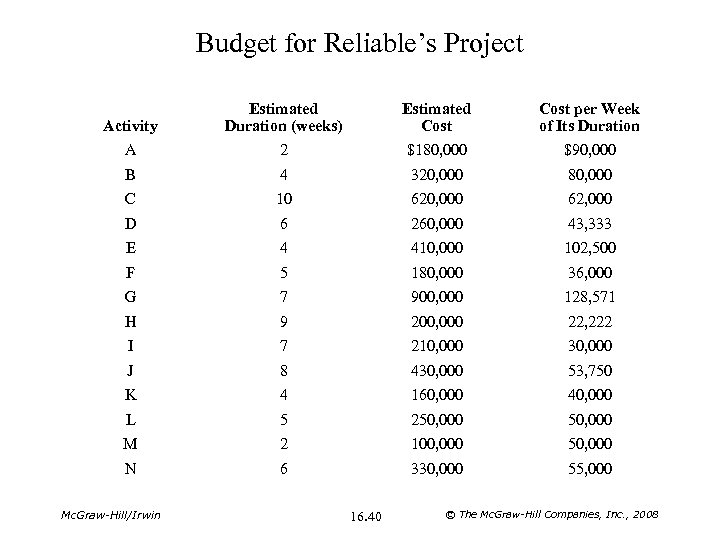
Budget for Reliable’s Project Activity Estimated Duration (weeks) Estimated Cost per Week of Its Duration A 2 $180, 000 $90, 000 B 4 320, 000 80, 000 C 10 620, 000 62, 000 D 6 260, 000 43, 333 E 4 410, 000 102, 500 F 5 180, 000 36, 000 G 7 900, 000 128, 571 H 9 200, 000 22, 222 I 7 210, 000 30, 000 J 8 430, 000 53, 750 K 4 160, 000 40, 000 L 5 250, 000 M 2 100, 000 50, 000 N 6 330, 000 55, 000 Mc. Graw-Hill/Irwin 16. 40 © The Mc. Graw-Hill Companies, Inc. , 2008
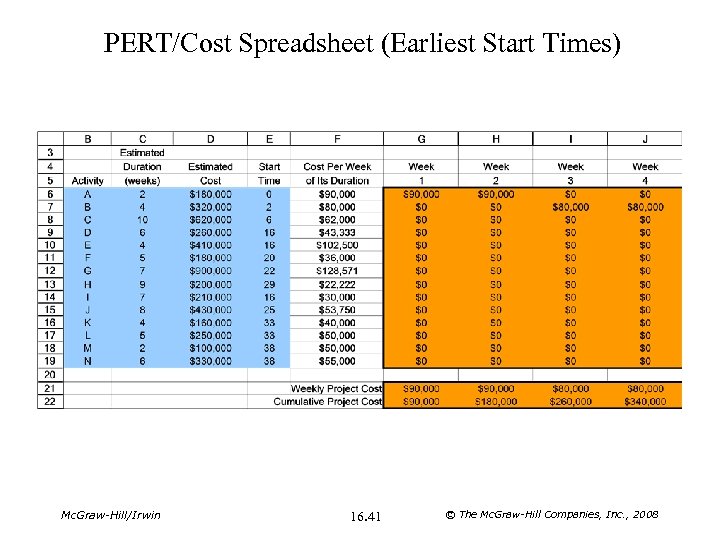
PERT/Cost Spreadsheet (Earliest Start Times) Mc. Graw-Hill/Irwin 16. 41 © The Mc. Graw-Hill Companies, Inc. , 2008
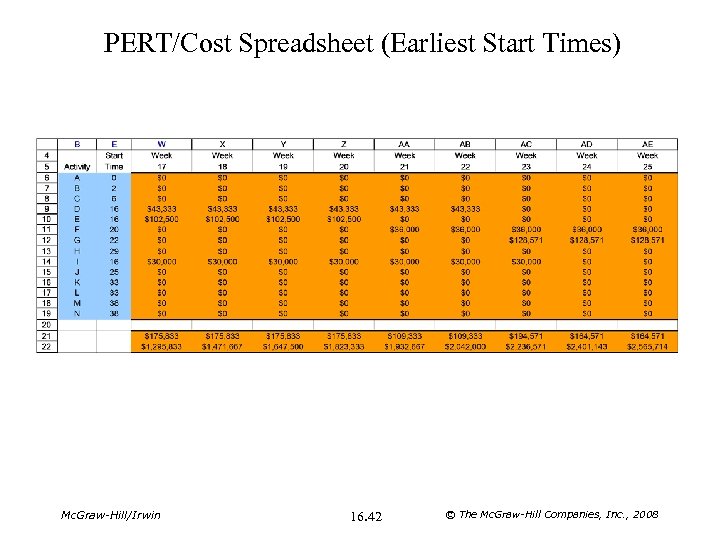
PERT/Cost Spreadsheet (Earliest Start Times) Mc. Graw-Hill/Irwin 16. 42 © The Mc. Graw-Hill Companies, Inc. , 2008
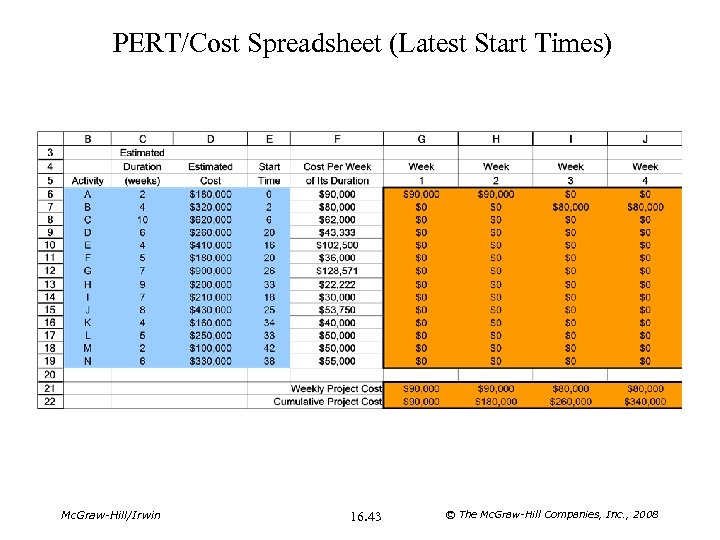
PERT/Cost Spreadsheet (Latest Start Times) Mc. Graw-Hill/Irwin 16. 43 © The Mc. Graw-Hill Companies, Inc. , 2008
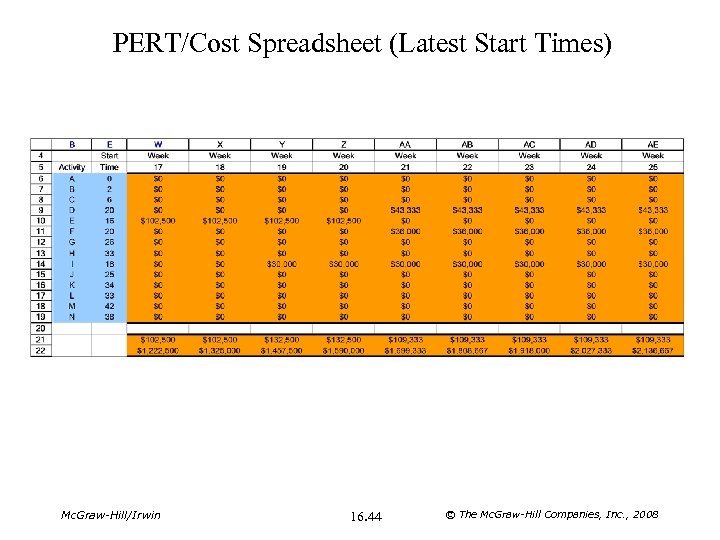
PERT/Cost Spreadsheet (Latest Start Times) Mc. Graw-Hill/Irwin 16. 44 © The Mc. Graw-Hill Companies, Inc. , 2008
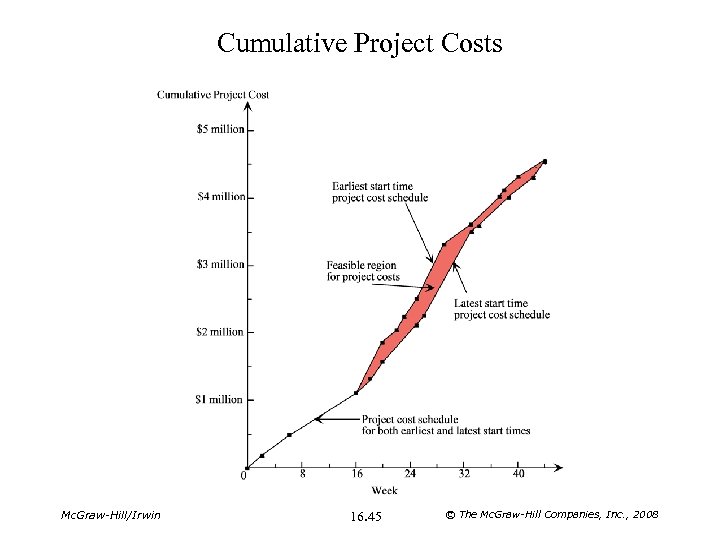
Cumulative Project Costs Mc. Graw-Hill/Irwin 16. 45 © The Mc. Graw-Hill Companies, Inc. , 2008
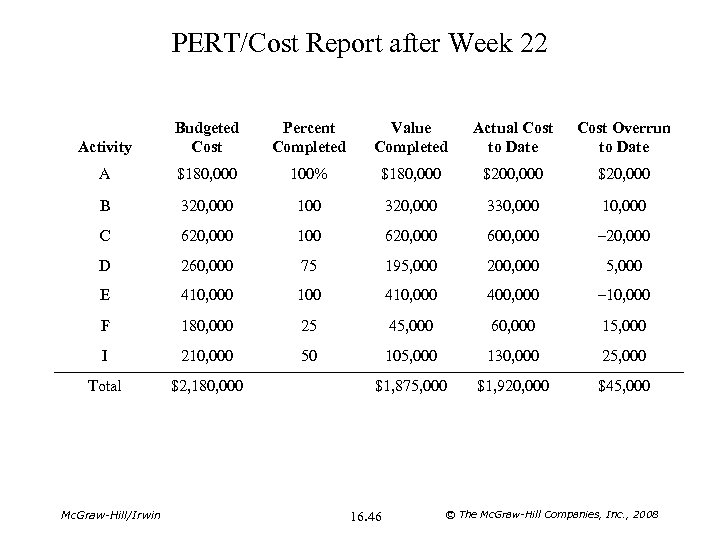
PERT/Cost Report after Week 22 Activity Budgeted Cost Percent Completed Value Completed Actual Cost to Date Cost Overrun to Date A $180, 000 100% $180, 000 $20, 000 B 320, 000 100 320, 000 330, 000 10, 000 C 620, 000 100 620, 000 600, 000 – 20, 000 D 260, 000 75 195, 000 200, 000 5, 000 E 410, 000 100 410, 000 400, 000 – 10, 000 F 180, 000 25 45, 000 60, 000 15, 000 I 210, 000 50 105, 000 130, 000 25, 000 Total $2, 180, 000 $1, 875, 000 $1, 920, 000 $45, 000 Mc. Graw-Hill/Irwin 16. 46 © The Mc. Graw-Hill Companies, Inc. , 2008

Example: Building a House Time (Days) Immediate Predecessor Foundation 4 — Framing 10 Foundation Plumbing 9 Framing Electrical 6 Framing Wall Board 8 Plumbing, Electrical Siding 16 Framing Paint Interior 5 Wall Board Paint Exterior 9 Siding Fixtures 6 Int. Paint, Ext. Paint Activity Mc. Graw-Hill/Irwin 16. 47 © The Mc. Graw-Hill Companies, Inc. , 2008
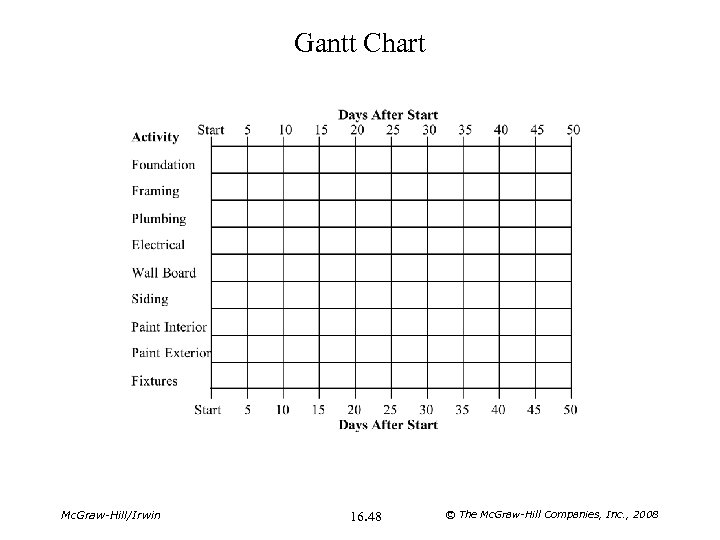
Gantt Chart Mc. Graw-Hill/Irwin 16. 48 © The Mc. Graw-Hill Companies, Inc. , 2008
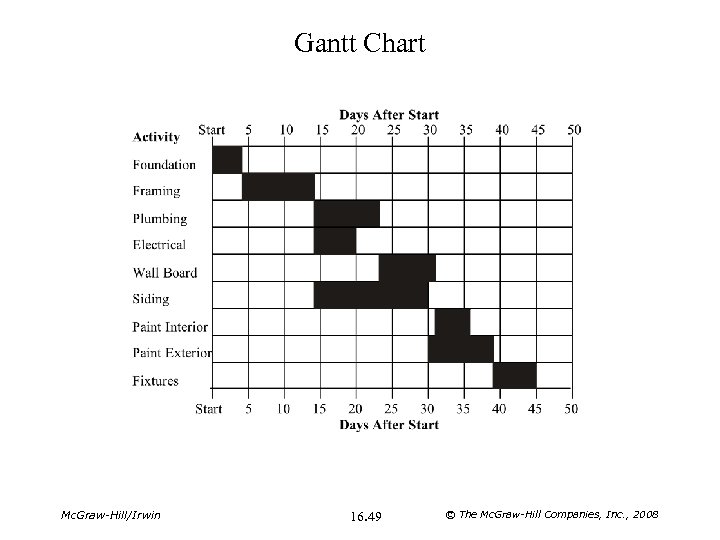
Gantt Chart Mc. Graw-Hill/Irwin 16. 49 © The Mc. Graw-Hill Companies, Inc. , 2008

PERT and CPM • Procedure 1. Determine the sequence of activities. 2. Construct the network or precedence diagram. 3. Starting from the left, compute the Early Start (ES) and Early Finish (EF) time for each activity. 4. Starting from the right, compute the Late Finish (LF) and Late Start (LS) time for each activity. 5. Find the slack for each activity. 6. Identify the Critical Path. Mc. Graw-Hill/Irwin 16. 50 © The Mc. Graw-Hill Companies, Inc. , 2008

Notation t Duration of an activity ES The earliest time an activity can start EF The earliest time an activity can finish (EF = ES + t) LS The latest time an activity can start and not delay the project LF The latest time an activity can finish and not delay the project Slack The extra time that could be made available to an activity without delaying the project (Slack = LS – ES) Critical Path The sequence(s) of activities with no slack Mc. Graw-Hill/Irwin 16. 51 © The Mc. Graw-Hill Companies, Inc. , 2008
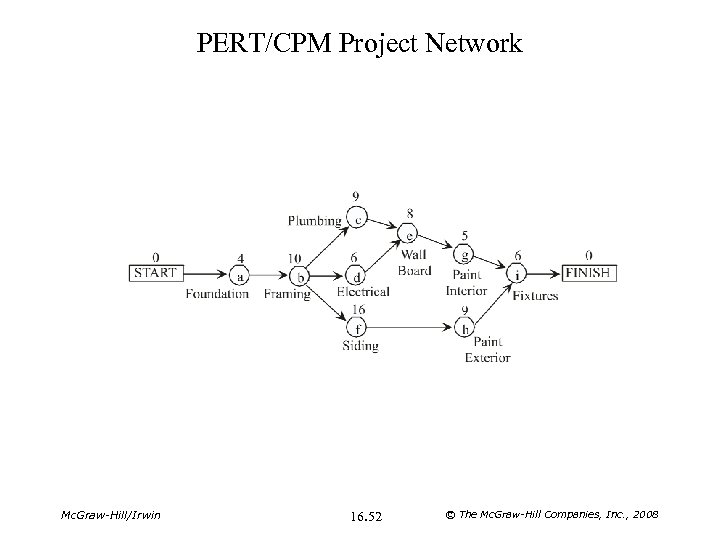
PERT/CPM Project Network Mc. Graw-Hill/Irwin 16. 52 © The Mc. Graw-Hill Companies, Inc. , 2008

Calculation of ES, EF, LS, and Slack • ES = Maximum of EF’s for all predecessors • EF = ES + t • LF = Minimum of ES for all successors • LS = LF – t • Slack = LS – ES = LF – EF Mc. Graw-Hill/Irwin 16. 53 © The Mc. Graw-Hill Companies, Inc. , 2008
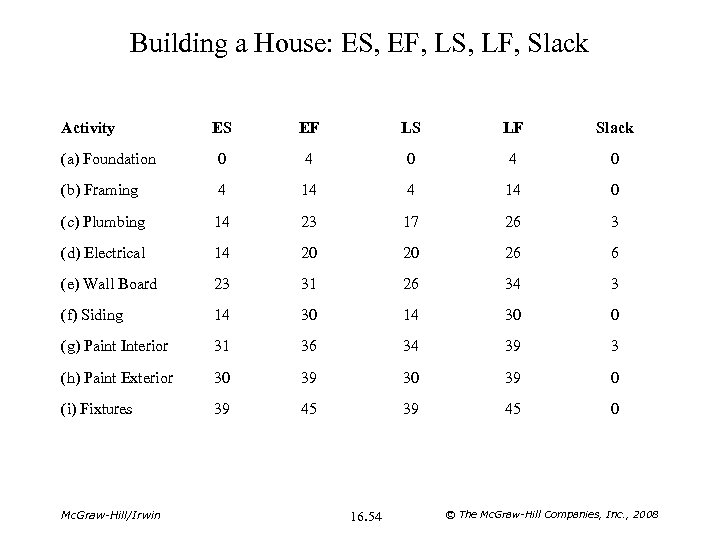
Building a House: ES, EF, LS, LF, Slack Activity ES EF LS LF Slack (a) Foundation 0 4 0 (b) Framing 4 14 0 (c) Plumbing 14 23 17 26 3 (d) Electrical 14 20 20 26 6 (e) Wall Board 23 31 26 34 3 (f) Siding 14 30 0 (g) Paint Interior 31 36 34 39 3 (h) Paint Exterior 30 39 0 (i) Fixtures 39 45 0 Mc. Graw-Hill/Irwin 16. 54 © The Mc. Graw-Hill Companies, Inc. , 2008
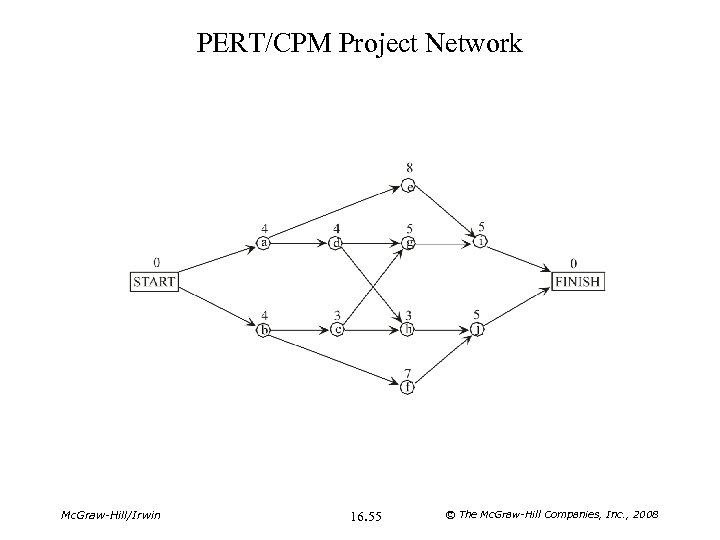
PERT/CPM Project Network Mc. Graw-Hill/Irwin 16. 55 © The Mc. Graw-Hill Companies, Inc. , 2008
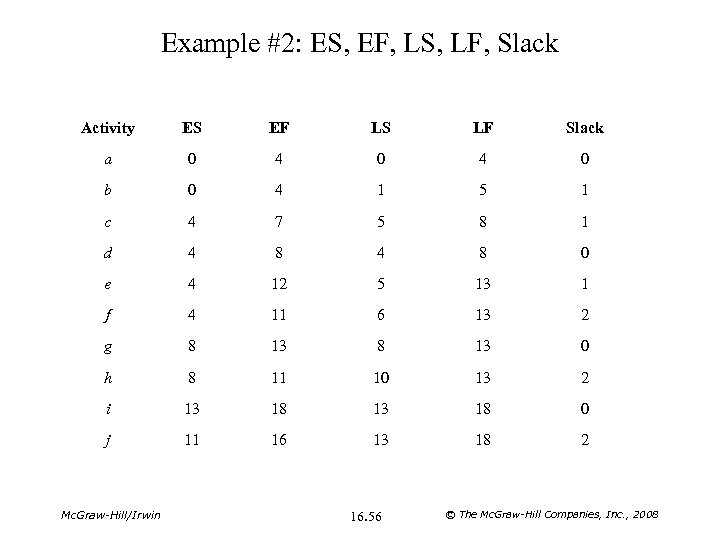
Example #2: ES, EF, LS, LF, Slack Activity ES EF LS LF Slack a 0 4 0 b 0 4 1 5 1 c 4 7 5 8 1 d 4 8 0 e 4 12 5 13 1 f 4 11 6 13 2 g 8 13 0 h 8 11 10 13 2 i 13 18 0 j 11 16 13 18 2 Mc. Graw-Hill/Irwin 16. 56 © The Mc. Graw-Hill Companies, Inc. , 2008

PERT with Uncertain Activity Durations • If the activity times are not known with certainty, PERT/CPM can be used to calculate the probability that the project will complete by time t. • For each activity, make three time estimates: – Optimistic time: o – Pessimistic time: p – Most-likely time: m Mc. Graw-Hill/Irwin 16. 57 © The Mc. Graw-Hill Companies, Inc. , 2008
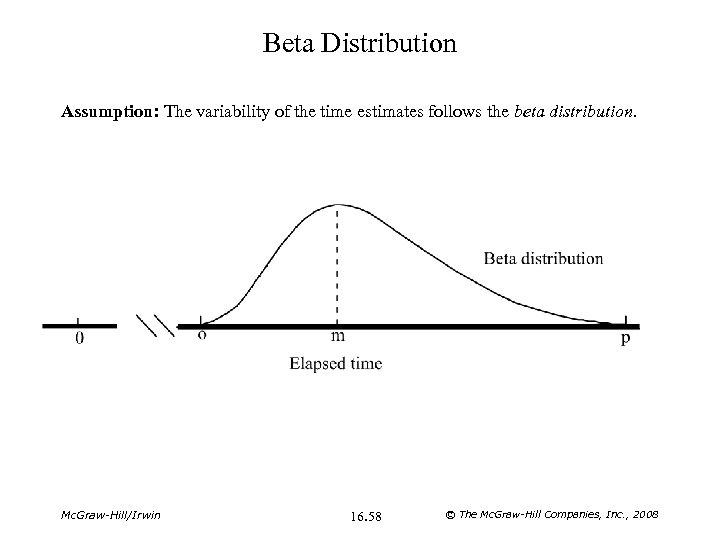
Beta Distribution Assumption: The variability of the time estimates follows the beta distribution. Mc. Graw-Hill/Irwin 16. 58 © The Mc. Graw-Hill Companies, Inc. , 2008

PERT with Uncertain Activity Durations Goal: Calculate the probability that the project is completed by time t. Procedure: 1. Calculate the expected duration and variance for each activity. 2. Calculate the expected length of each path. Determine which path is the mean critical path. 3. Calculate the standard deviation of the mean critical path. 4. Find the probability that the mean critical path completes by time t. Mc. Graw-Hill/Irwin 16. 59 © The Mc. Graw-Hill Companies, Inc. , 2008

Expected Duration and Variance for Activities (Step #1) • The expected duration of each activity can be approximated as follows: • The variance of the duration for each activity can be approximated as follows: Mc. Graw-Hill/Irwin 16. 60 © The Mc. Graw-Hill Companies, Inc. , 2008

Expected Length of Each Path (Step #2) • The expected length of each path is equal to the sum of the expected durations of all the activities on each path. • The mean critical path is the path with the longest expected length. Mc. Graw-Hill/Irwin 16. 61 © The Mc. Graw-Hill Companies, Inc. , 2008

Standard Deviation of Mean Critical Path (Step #3) • The variance of the length of the path is the sum of the variances of all the activities on the path. s 2 path = ∑ all activities on path s 2 • The standard deviation of the length of the path is the square root of the variance. Mc. Graw-Hill/Irwin 16. 62 © The Mc. Graw-Hill Companies, Inc. , 2008
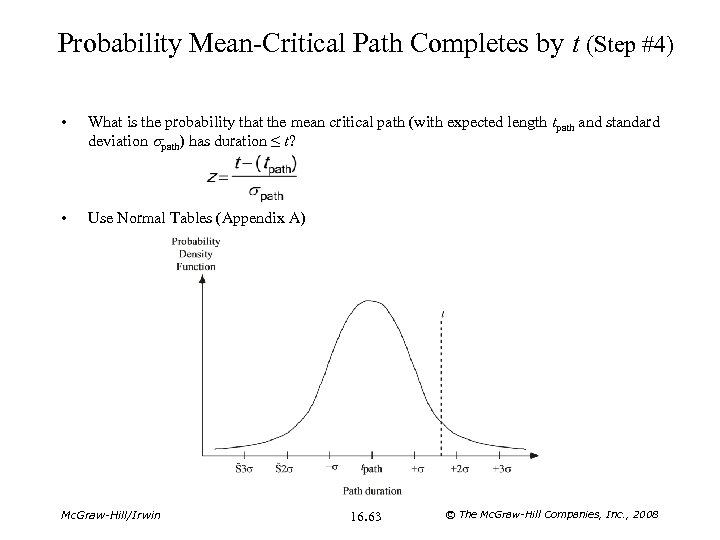
Probability Mean-Critical Path Completes by t (Step #4) • What is the probability that the mean critical path (with expected length tpath and standard deviation spath) has duration ≤ t? • Use Normal Tables (Appendix A) Mc. Graw-Hill/Irwin 16. 63 © The Mc. Graw-Hill Companies, Inc. , 2008
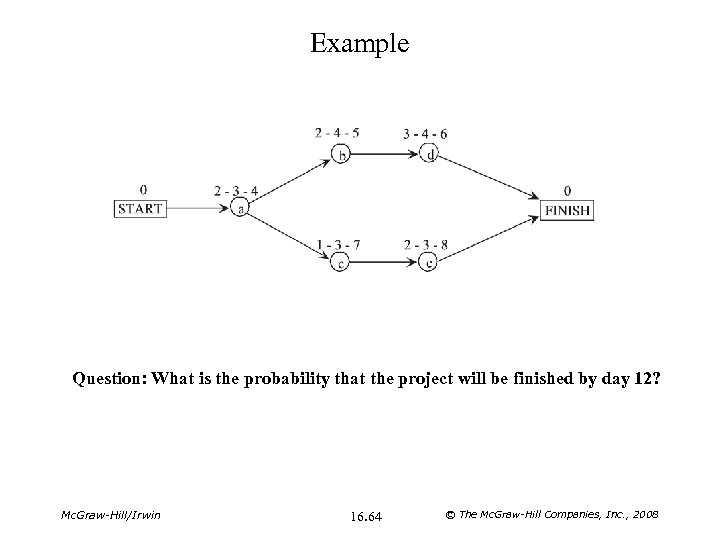
Example Question: What is the probability that the project will be finished by day 12? Mc. Graw-Hill/Irwin 16. 64 © The Mc. Graw-Hill Companies, Inc. , 2008
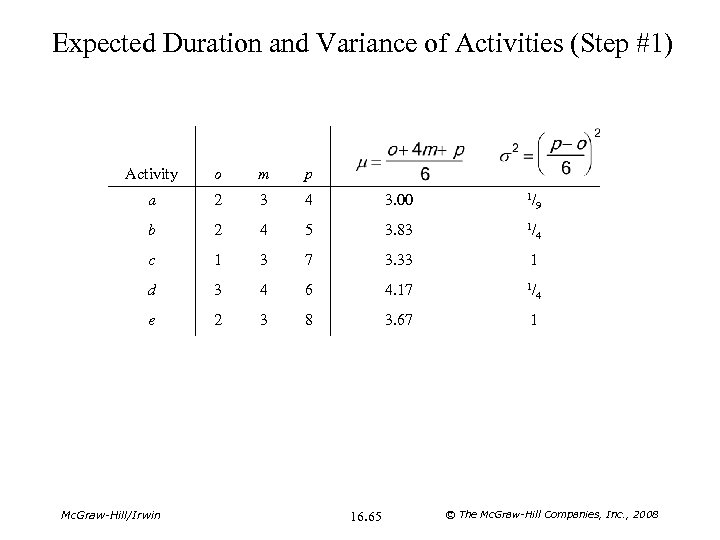
Expected Duration and Variance of Activities (Step #1) Activity o m p a 2 3 4 3. 00 1/ 9 b 2 4 5 3. 83 1/ 4 c 1 3 7 3. 33 1 d 3 4 6 4. 17 1/ e 2 3 8 3. 67 1 Mc. Graw-Hill/Irwin 16. 65 4 © The Mc. Graw-Hill Companies, Inc. , 2008

Expected Length of Each Path (Step #2) Path Expected Length of Path a - b - d 3. 00 + 3. 83 + 4. 17 = 11 a - c - e 3. 00 + 3. 33 + 3. 67 = 10 The mean-critical path is a - b - d. Mc. Graw-Hill/Irwin 16. 66 © The Mc. Graw-Hill Companies, Inc. , 2008

Standard Deviation of Mean-Critical Path (Step #3) • The variance of the length of the path is the sum of the variances of all the activities on the path. s 2 path = ∑ all activities on path s 2 = 1/9 + 1/4 = 0. 61 • The standard deviation of the length of the path is the square root of the variance. Mc. Graw-Hill/Irwin 16. 67 © The Mc. Graw-Hill Companies, Inc. , 2008

Probability Mean-Critical Path Completes by t=12 (Step #4) • The probability that the mean critical path (with expected length 11 and standard deviation 0. 71) has duration ≤ 12? • Then, from Normal Table: Prob(Project ≤ 12) = Prob(z ≤ 1. 41) = 0. 92 Mc. Graw-Hill/Irwin 16. 68 © The Mc. Graw-Hill Companies, Inc. , 2008

Time-Cost Tradeoffs • It is often possible to expedite activities at extra cost (called “crashing”). • Benefits of completing a project earlier: – Monetary incentives for timely or early completion of project – Beating the competition to the market – Reduce indirect cost • Procedure: 1. 2. 3. 4. Obtain estimates of regular and crash times and costs for each activity. Determine the lengths of all paths using regular time for each activity. Identify the critical path(s) Crash activities on the critical path(s) in order of increasing cost as long as crashing costs do not exceed benefits. Mc. Graw-Hill/Irwin 16. 69 © The Mc. Graw-Hill Companies, Inc. , 2008
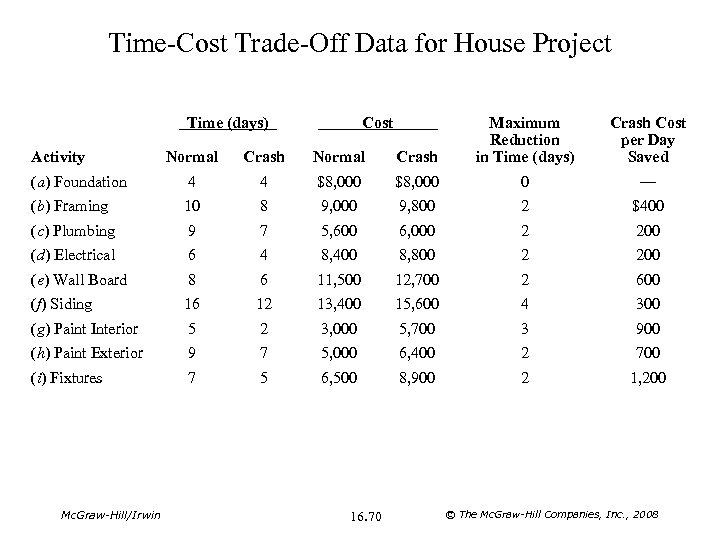
Time-Cost Trade-Off Data for House Project Normal Crash Maximum Reduction in Time (days) (a) Foundation 4 4 $8, 000 0 — (b) Framing 10 8 9, 000 9, 800 2 $400 (c) Plumbing 9 7 5, 600 6, 000 2 200 (d) Electrical 6 4 8, 400 8, 800 2 200 (e) Wall Board 8 6 11, 500 12, 700 2 600 (f) Siding 16 12 13, 400 15, 600 4 300 (g) Paint Interior 5 2 3, 000 5, 700 3 900 (h) Paint Exterior 9 7 5, 000 6, 400 2 700 (i) Fixtures 7 5 6, 500 8, 900 2 1, 200 Time (days) Activity Mc. Graw-Hill/Irwin Cost 16. 70 Crash Cost per Day Saved © The Mc. Graw-Hill Companies, Inc. , 2008
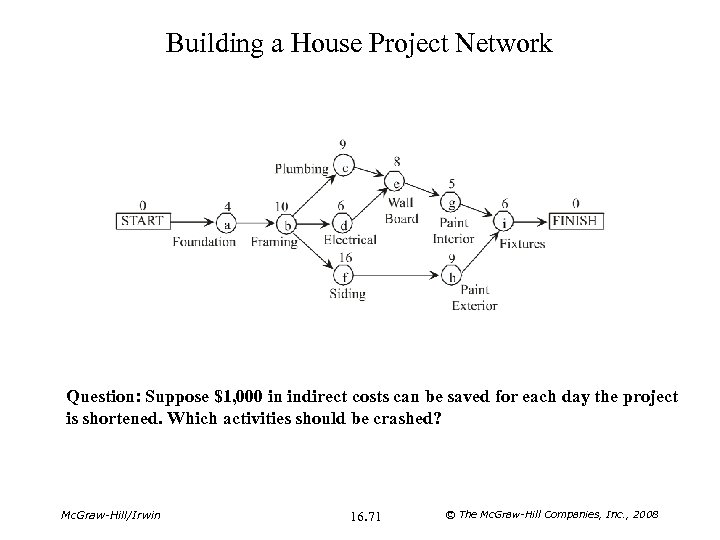
Building a House Project Network Question: Suppose $1, 000 in indirect costs can be saved for each day the project is shortened. Which activities should be crashed? Mc. Graw-Hill/Irwin 16. 71 © The Mc. Graw-Hill Companies, Inc. , 2008
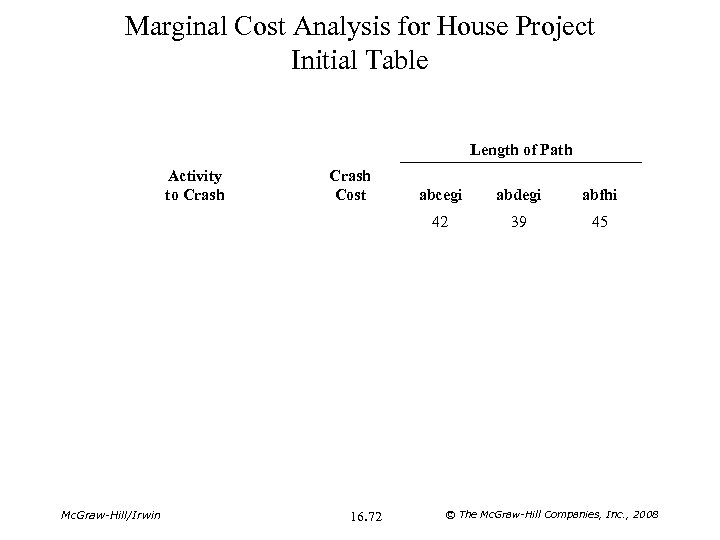
Marginal Cost Analysis for House Project Initial Table Length of Path Activity to Crash Cost 16. 72 abdegi abfhi 42 Mc. Graw-Hill/Irwin abcegi 39 45 © The Mc. Graw-Hill Companies, Inc. , 2008
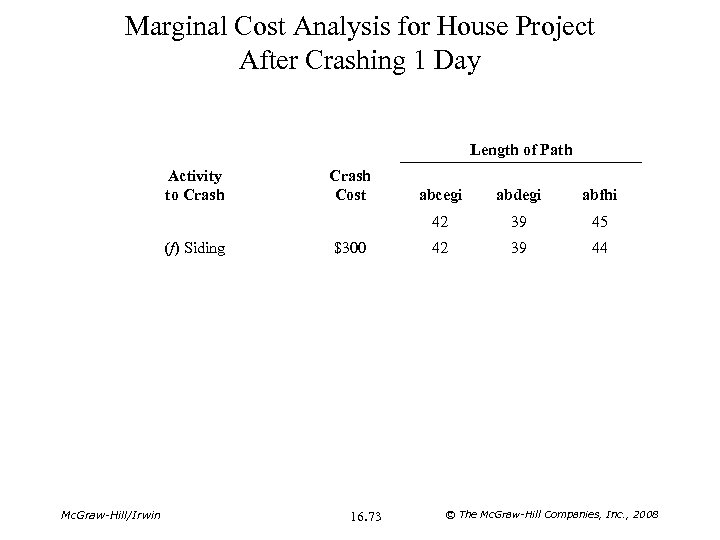
Marginal Cost Analysis for House Project After Crashing 1 Day Length of Path Activity to Crash Cost Mc. Graw-Hill/Irwin $300 16. 73 abdegi abfhi 42 (f) Siding abcegi 39 45 42 39 44 © The Mc. Graw-Hill Companies, Inc. , 2008
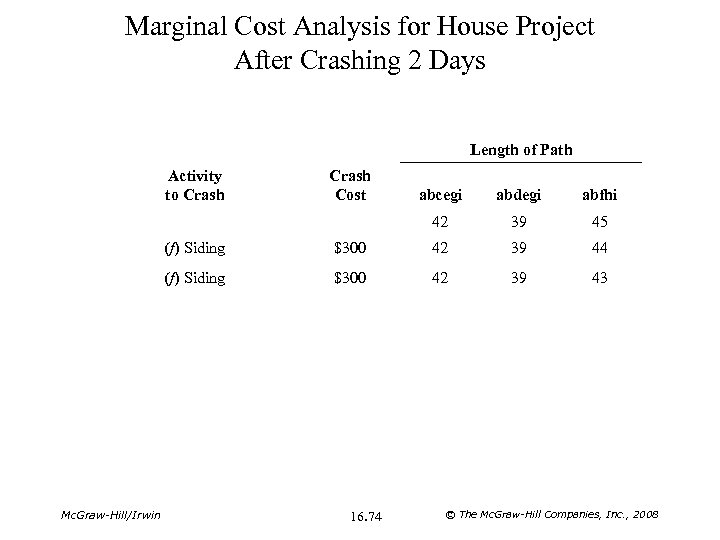
Marginal Cost Analysis for House Project After Crashing 2 Days Length of Path Activity to Crash Cost abcegi abdegi abfhi 42 39 45 (f) Siding 42 39 44 (f) Siding Mc. Graw-Hill/Irwin $300 42 39 43 16. 74 © The Mc. Graw-Hill Companies, Inc. , 2008
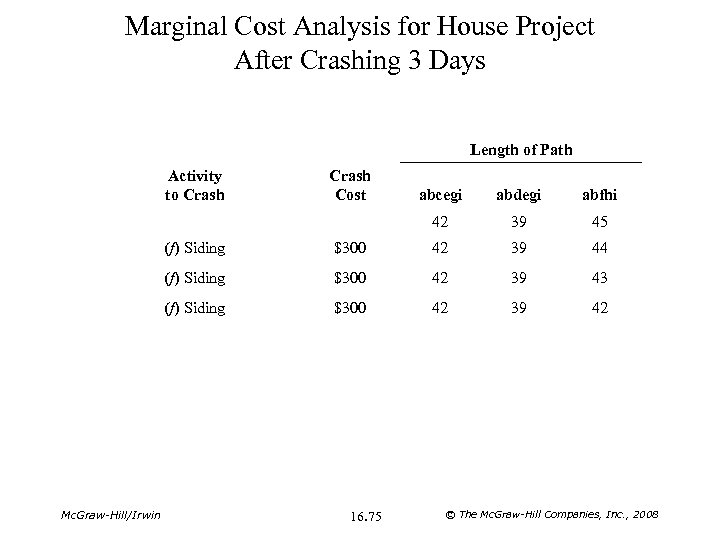
Marginal Cost Analysis for House Project After Crashing 3 Days Length of Path Activity to Crash Cost abcegi abdegi abfhi 42 39 45 (f) Siding 42 39 44 (f) Siding $300 42 39 43 (f) Siding Mc. Graw-Hill/Irwin $300 42 39 42 16. 75 © The Mc. Graw-Hill Companies, Inc. , 2008
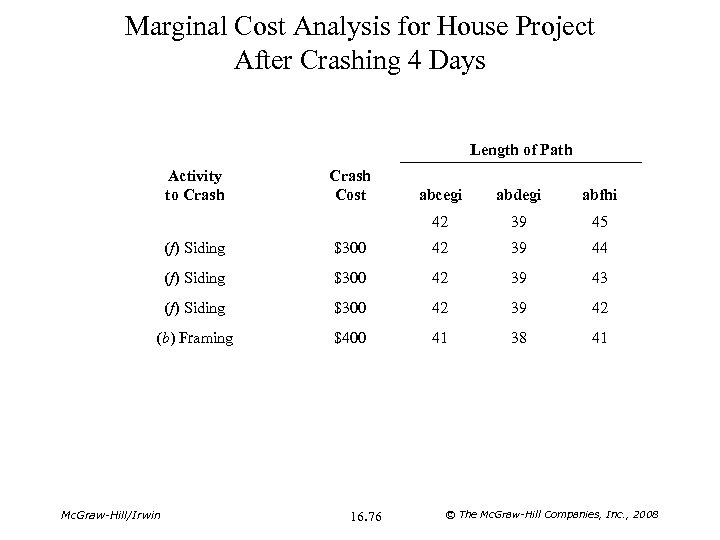
Marginal Cost Analysis for House Project After Crashing 4 Days Length of Path Activity to Crash Cost abcegi abdegi abfhi 42 39 45 (f) Siding $300 42 39 44 (f) Siding $300 42 39 43 (f) Siding $300 42 39 42 (b) Framing $400 41 38 41 Mc. Graw-Hill/Irwin 16. 76 © The Mc. Graw-Hill Companies, Inc. , 2008
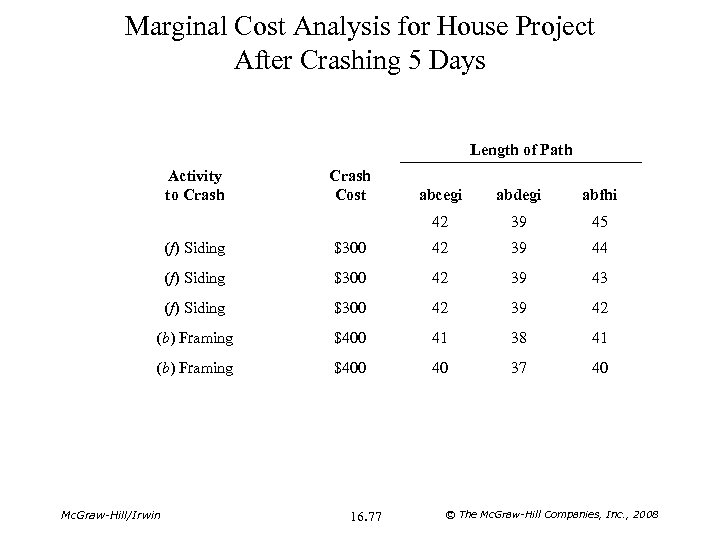
Marginal Cost Analysis for House Project After Crashing 5 Days Length of Path Activity to Crash Cost abcegi abdegi abfhi 42 39 45 (f) Siding $300 42 39 44 (f) Siding $300 42 39 43 (f) Siding $300 42 39 42 (b) Framing $400 41 38 41 (b) Framing $400 40 37 40 Mc. Graw-Hill/Irwin 16. 77 © The Mc. Graw-Hill Companies, Inc. , 2008
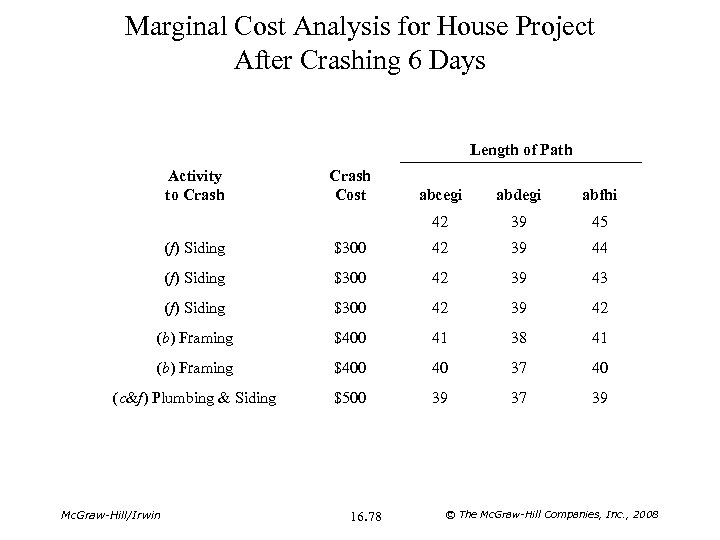
Marginal Cost Analysis for House Project After Crashing 6 Days Length of Path Activity to Crash Cost abcegi abdegi abfhi 42 39 45 (f) Siding $300 42 39 44 (f) Siding $300 42 39 43 (f) Siding $300 42 39 42 (b) Framing $400 41 38 41 (b) Framing $400 40 37 40 (c&f) Plumbing & Siding $500 39 37 39 Mc. Graw-Hill/Irwin 16. 78 © The Mc. Graw-Hill Companies, Inc. , 2008
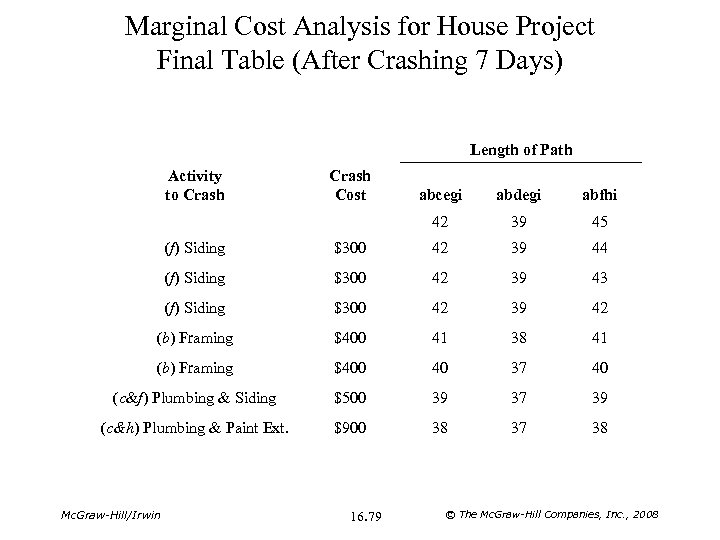
Marginal Cost Analysis for House Project Final Table (After Crashing 7 Days) Length of Path Activity to Crash Cost abcegi abdegi abfhi 42 39 45 (f) Siding $300 42 39 44 (f) Siding $300 42 39 43 (f) Siding $300 42 39 42 (b) Framing $400 41 38 41 (b) Framing $400 40 37 40 (c&f) Plumbing & Siding $500 39 37 39 (c&h) Plumbing & Paint Ext. $900 38 37 38 Mc. Graw-Hill/Irwin 16. 79 © The Mc. Graw-Hill Companies, Inc. , 2008

Marginal Cost Analysis for House Project • Seven days have been saved off the length of the project (38 days rather than 45). – $7, 000 saved in indirect costs. • The total crashing costs were – $300 + $400 + $500 + $900 = $2, 700 • Total savings = $7, 000 – $2, 700 = $5, 300. Mc. Graw-Hill/Irwin 16. 80 © The Mc. Graw-Hill Companies, Inc. , 2008
6a35289d94687f4a9884b9687cfa3bb8.ppt