Т. В. Безрукова Инженерная

Т. В. Безрукова Инженерная и компьютерная графика Лекция № 7 Основные позиционные задачи на комплексном чертеже. Пересечение линии с поверхностью

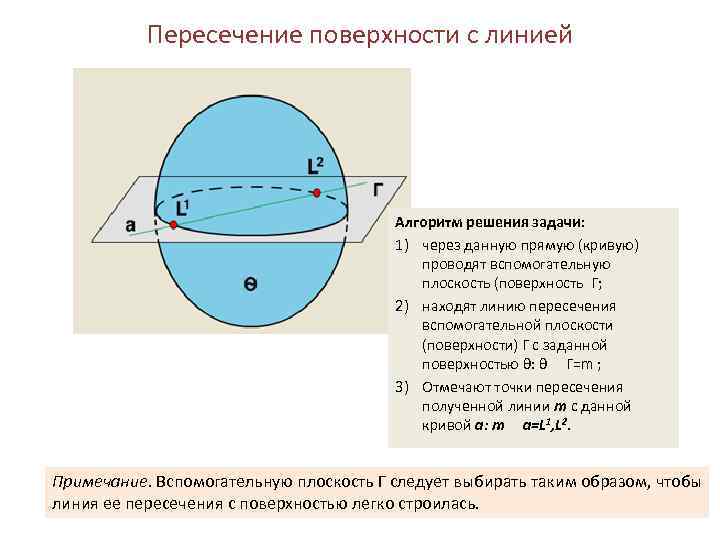
Пересечение поверхности с линией Алгоритм решения задачи: 1) через данную прямую (кривую) проводят вспомогательную плоскость (поверхность Г; 2) находят линию пересечения вспомогательной плоскости (поверхности) Г с заданной поверхностью θ: θ Г=m ; 3) Отмечают точки пересечения полученной линии m с данной кривой a: m a=L 1, L 2. Примечание. Вспомогательную плоскость Г следует выбирать таким образом, чтобы линия ее пересечения с поверхностью легко строилась.

Пересечение поверхности с прямой Пример 1. Даны прямая m и тор. Построить точки пересечения прямой m и поверхности . Решение. 1. Заключаем линию m во фронтально проецирующую вспомогательную плоскость ( 2 ). Определяем линию n пересечения вспомогательной плоскости с поверхностью , фронтально конкурирующую с заданной прямой m. Линии n и m пересекаются, т. к. они находятся в одной фронтально проецирующей плоскости. 2. Определяем горизонтальную проекцию линии n (n 1 ), исходя из условия принадлежности ее поверхности. 3. Находим точки Α и Β пересечения линий n и m, которые и являются искомыми. 4. Устанавливаем видимость проекций прямой. Так как участок ΑΒ прямой m, расположен внутри поверхности, то он невидим на Π 1 и Π 2. Кроме этого, на Π 2 невидим отрезок прямой m правее точки Β 2 до точки на очерке поверхности, а на Π 1 – левее точки 5 1 , также до точки на очерке поверхности. Эти отрезки закрыты поверхностью – находятся за контурами поверхности.

Пересечение поверхности с прямой В некоторых случаях показ вспомогательной плоскости излишен. Например, точки встречи прямой l с поверхностью прямого кругового цилиндра, имеющего вертикальную ось, определяют следующим образом. Горизонтальная проекция цилиндрической поверхности представляет собой окружность, поэтому горизонтальные проекции всех точек, расположенных на цилиндрической поверхности, в том числе и двух искомых точек встречи, будут расположены на этой же окружности. Фронтальные проекции А 2 и В 2 искомых точек встречи определяют проведением через точки А 1 и В 1 вертикальных линий связи до пересечения с фронтальной проекцией l 2 прямой l. Во втором примере построена точка пересечения горизонтально-проецирующей прямой с поверхностью кругового конуса. В этом случае также нет необходимости применять вспомогательную плоскость. Горизонтальная проекция А 1 искомой точки совпадает с горизонтальной проекцией l 1 данной прямой. Фронтальная проекция точки А (А 2) определяется с помощью образующей S 1 конуса.

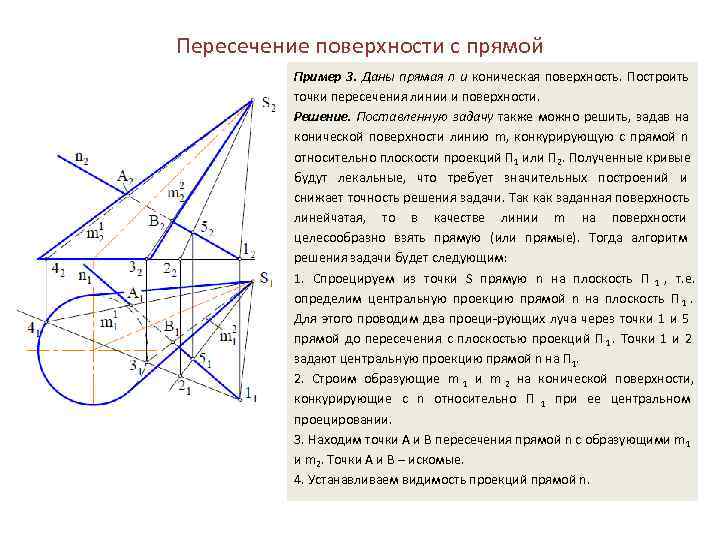
Пересечение поверхности с прямой Пример 3. Даны прямая n и коническая поверхность. Построить точки пересечения линии и поверхности. Решение. Поставленную задачу также можно решить, задав на конической поверхности линию m, конкурирующую с прямой n относительно плоскости проекций Π 1 или Π 2. Полученные кривые будут лекальные, что требует значительных построений и снижает точность решения задачи. Так как заданная поверхность линейчатая, то в качестве линии m на поверхности целесообразно взять прямую (или прямые). Тогда алгоритм решения задачи будет следующим: 1. Спроецируем из точки S прямую n на плоскость Π 1 , т. е. определим центральную проекцию прямой n на плоскость Π 1. Для этого проводим два проеци-рующих луча через точки 1 и 5 прямой до пересечения с плоскостью проекций Π 1. Точки 1 и 2 задают центральную проекцию прямой n на Π 1. 2. Строим образующие m 1 и m 2 на конической поверхности, конкурирующие с n относительно П 1 при ее центральном проецировании. 3. Находим точки Α и Β пересечения прямой n с образующими m 1 и m 2. Точки Α и Β – искомые. 4. Устанавливаем видимость проекций прямой n.

Пересечение плоскости с прямой Частный случай пересечения поверхности с плоскостью, когда поверхность является поверхностью 1 -го порядка, т. е. плоскостью. Рассмотрим порядок определения точки пересечения прямой m с плоскостью, заданной треугольником АВС и следами Г (Г 1, Г 2) Чтобы определить точку пересечения прямой m с плоскостью, заданной треугольником АВС, необходимо выполнить следующее: 1) провести через прямую m фронтально-проецирующую плоскость Р (Р 2); 2) определить линию пересечения плоскости Р и треугольника АВС 12 (1222 и 1121); 3) определить точку пересечения прямой m (m 1 , m 2 ) треугольником АВС. Эта точка находится на линии пересечения плоскостей Р и треугольника АВС – 12 (1 1 2 1 и 1 2 2 2 ). Сначал определяем горизонтальную проекцию К 1, а затем фронтальную К 2. В заключение необходимо определить видимые и невидимые части прямой m относительно плоскостей проекций П 1 и П 2, считая, что треугольник АВС является непрозрачным. Для этого необходимо сравнить положение в пространстве двух конкурирующих точек, одна из которых принадлежит прямой m, а вторая – стороне треугольника АВС.

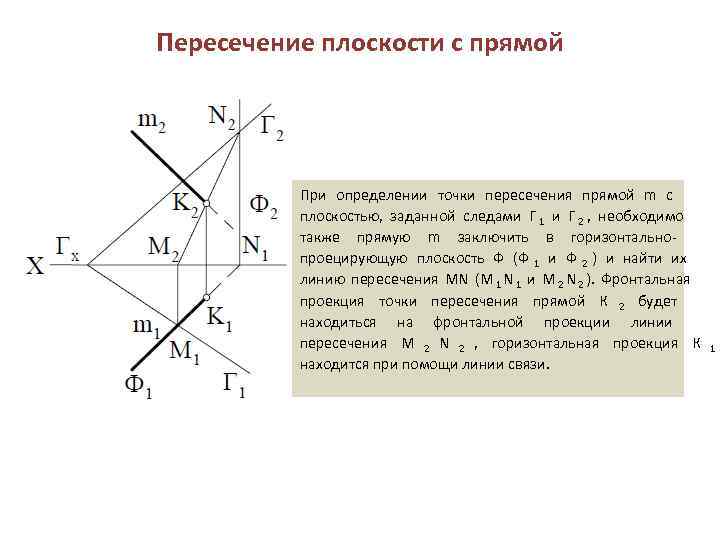
Пересечение плоскости с прямой При определении точки пересечения прямой m с плоскостью, заданной следами Г 1 и Г 2 , необходимо также прямую m заключить в горизонтально- проецирующую плоскость Ф (Ф 1 и Ф 2 ) и найти их линию пересечения MN (M 1 N 1 и M 2 N 2 ). Фронтальная проекция точки пересечения прямой К 2 будет находиться на фронтальной проекции линии пересечения M 2 N 2 , горизонтальная проекция К 1 находится при помощи линии связи.

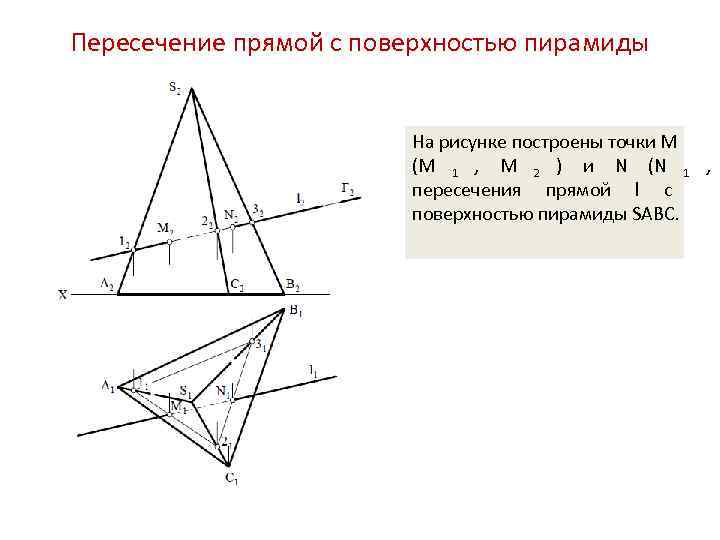
Пересечение прямой с поверхностью пирамиды На рисунке построены точки M (М 1 , М 2 ) и N (N 1 , пересечения прямой l с поверхностью пирамиды SABC.

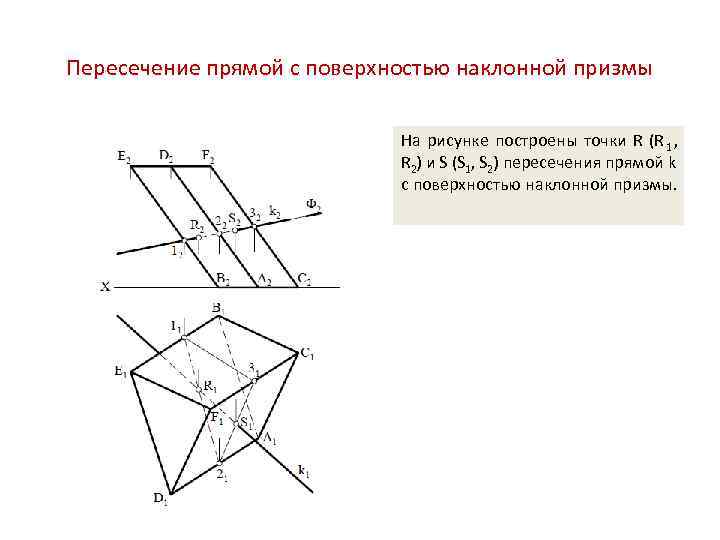
Пересечение прямой с поверхностью наклонной призмы На рисунке построены точки R (R 1 , R 2) и S (S 1, S 2) пересечения прямой k с поверхностью наклонной призмы.