 © T Madas
© T Madas
 © T Madas
© T Madas
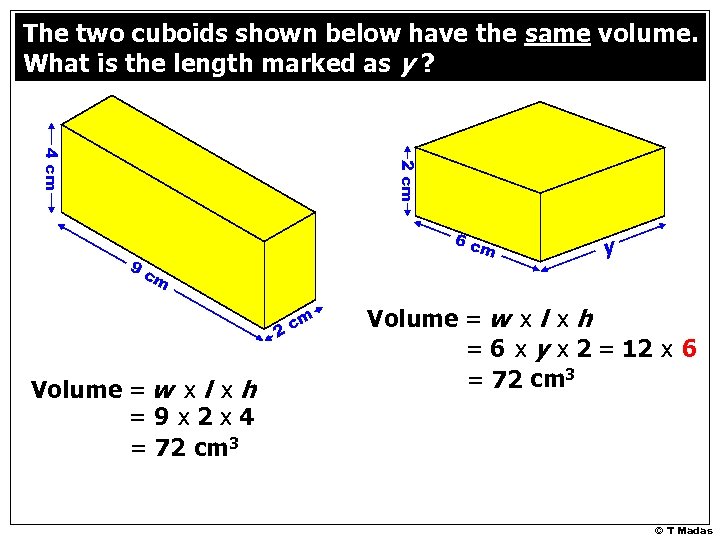 The two cuboids shown below have the same volume. What is the length marked as y ? 2 cm 4 cm 6 c m 9 c m m 2 c Volume = w x l x h =9 x 2 x 4 = 72 cm 3 y Volume = w x l x h 6 = 6 x y x 2 = 12 x y = 72 cm 3 © T Madas
The two cuboids shown below have the same volume. What is the length marked as y ? 2 cm 4 cm 6 c m 9 c m m 2 c Volume = w x l x h =9 x 2 x 4 = 72 cm 3 y Volume = w x l x h 6 = 6 x y x 2 = 12 x y = 72 cm 3 © T Madas
 © T Madas
© T Madas
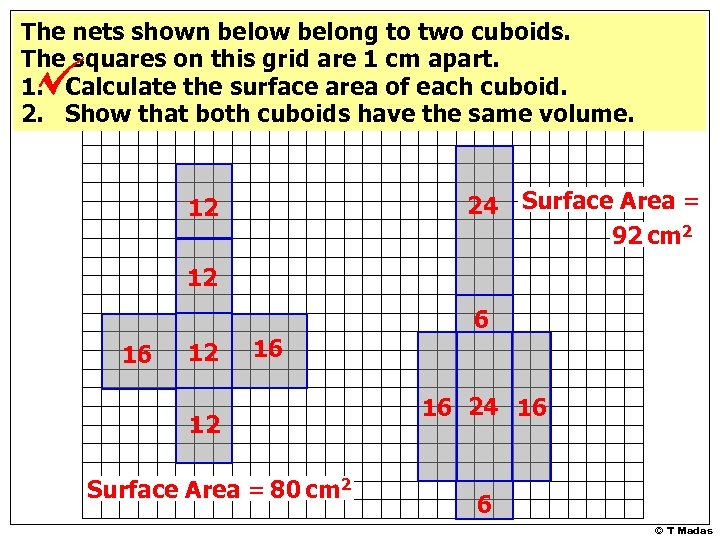 The nets shown below belong to two cuboids. The squares on this grid are 1 cm apart. 1. Calculate the surface area of each cuboid. 2. Show that both cuboids have the same volume. 24 12 Surface Area = 92 cm 2 12 6 16 12 Surface Area = 80 cm 2 16 24 16 6 © T Madas
The nets shown below belong to two cuboids. The squares on this grid are 1 cm apart. 1. Calculate the surface area of each cuboid. 2. Show that both cuboids have the same volume. 24 12 Surface Area = 92 cm 2 12 6 16 12 Surface Area = 80 cm 2 16 24 16 6 © T Madas
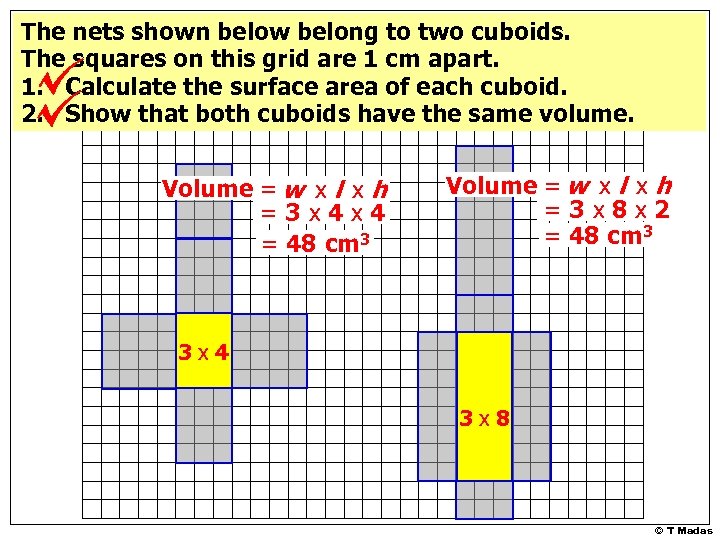 The nets shown below belong to two cuboids. The squares on this grid are 1 cm apart. 1. Calculate the surface area of each cuboid. 2. Show that both cuboids have the same volume. Volume = w x l x h =3 x 4 x 4 = 48 cm 3 Volume = w x l x h =3 x 8 x 2 = 48 cm 3 3 x 4 3 x 8 © T Madas
The nets shown below belong to two cuboids. The squares on this grid are 1 cm apart. 1. Calculate the surface area of each cuboid. 2. Show that both cuboids have the same volume. Volume = w x l x h =3 x 4 x 4 = 48 cm 3 Volume = w x l x h =3 x 8 x 2 = 48 cm 3 3 x 4 3 x 8 © T Madas
 © T Madas
© T Madas
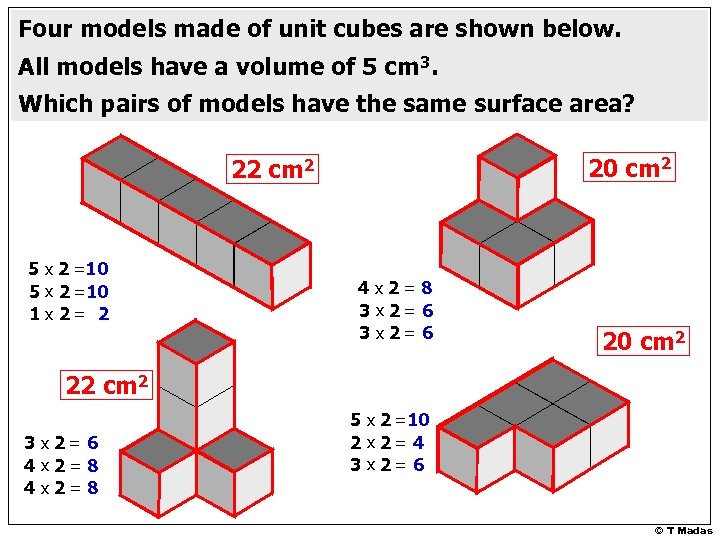 Four models made of unit cubes are shown below. All models have a volume of 5 cm 3. Which pairs of models have the same surface area? 20 cm 2 22 cm 2 5 x 2 =10 1 x 2= 2 4 x 2= 8 3 x 2= 6 20 cm 2 22 cm 2 3 x 2= 6 4 x 2= 8 5 x 2 =10 2 x 2= 4 3 x 2= 6 © T Madas
Four models made of unit cubes are shown below. All models have a volume of 5 cm 3. Which pairs of models have the same surface area? 20 cm 2 22 cm 2 5 x 2 =10 1 x 2= 2 4 x 2= 8 3 x 2= 6 20 cm 2 22 cm 2 3 x 2= 6 4 x 2= 8 5 x 2 =10 2 x 2= 4 3 x 2= 6 © T Madas
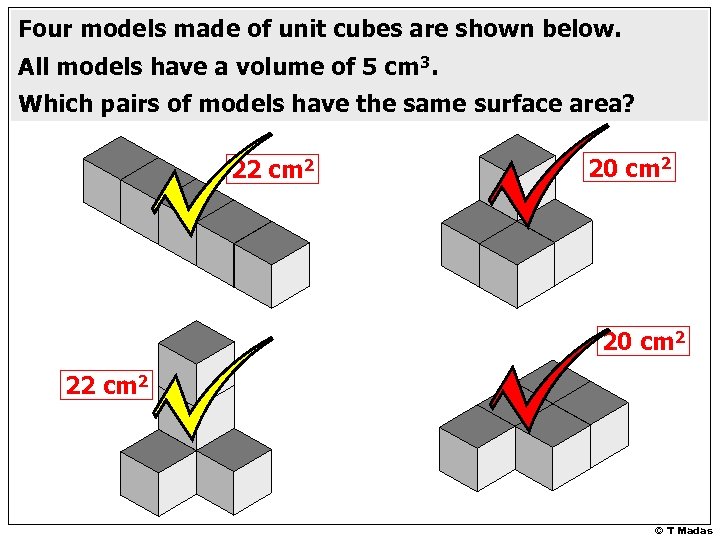 Four models made of unit cubes are shown below. All models have a volume of 5 cm 3. Which pairs of models have the same surface area? 22 cm 2 20 cm 2 22 cm 2 © T Madas
Four models made of unit cubes are shown below. All models have a volume of 5 cm 3. Which pairs of models have the same surface area? 22 cm 2 20 cm 2 22 cm 2 © T Madas
 © T Madas
© T Madas
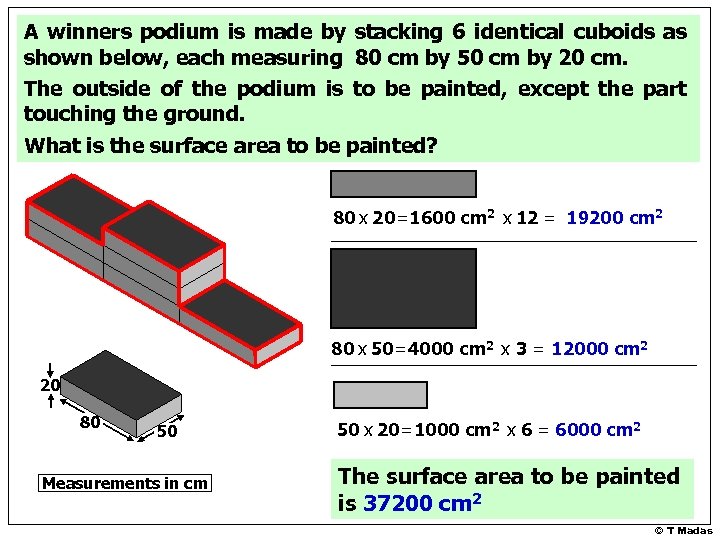 A winners podium is made by stacking 6 identical cuboids as shown below, each measuring 80 cm by 50 cm by 20 cm. The outside of the podium is to be painted, except the part touching the ground. What is the surface area to be painted? 80 x 20=1600 cm 2 x 12 = 19200 cm 2 80 x 50=4000 cm 2 x 3 = 12000 cm 2 20 80 50 Measurements in cm 50 x 20=1000 cm 2 x 6 = 6000 cm 2 The surface area to be painted is 37200 cm 2 © T Madas
A winners podium is made by stacking 6 identical cuboids as shown below, each measuring 80 cm by 50 cm by 20 cm. The outside of the podium is to be painted, except the part touching the ground. What is the surface area to be painted? 80 x 20=1600 cm 2 x 12 = 19200 cm 2 80 x 50=4000 cm 2 x 3 = 12000 cm 2 20 80 50 Measurements in cm 50 x 20=1000 cm 2 x 6 = 6000 cm 2 The surface area to be painted is 37200 cm 2 © T Madas
 © T Madas
© T Madas
 A petrol can is in the shape of a cuboid with the measurements given in the figure below. Calculate the capacity of this can in litres. Volume of a cuboid length x width x height 40 cm V = lwh V = 30 x 15 x 40 30 cm 15 cm V = 18000 cm 3 © T Madas
A petrol can is in the shape of a cuboid with the measurements given in the figure below. Calculate the capacity of this can in litres. Volume of a cuboid length x width x height 40 cm V = lwh V = 30 x 15 x 40 30 cm 15 cm V = 18000 cm 3 © T Madas
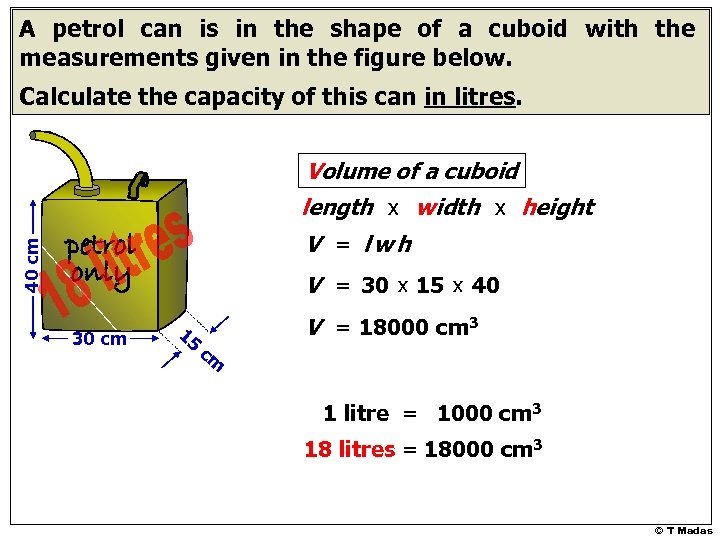 A petrol can is in the shape of a cuboid with the measurements given in the figure below. Calculate the capacity of this can in litres. Volume of a cuboid length x width x height 40 cm V = lwh V = 30 x 15 x 40 30 cm 15 cm V = 18000 cm 3 1 litre = 1000 cm 3 18 litres = 18000 cm 3 © T Madas
A petrol can is in the shape of a cuboid with the measurements given in the figure below. Calculate the capacity of this can in litres. Volume of a cuboid length x width x height 40 cm V = lwh V = 30 x 15 x 40 30 cm 15 cm V = 18000 cm 3 1 litre = 1000 cm 3 18 litres = 18000 cm 3 © T Madas
 © T Madas
© T Madas
 A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a water tank, also in the shape of a cuboid, measuring 50 cm by 30 cm by 40 cm. 1. Calculate the capacity of the water can in litres. 2. How many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 © T Madas
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a water tank, also in the shape of a cuboid, measuring 50 cm by 30 cm by 40 cm. 1. Calculate the capacity of the water can in litres. 2. How many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 © T Madas
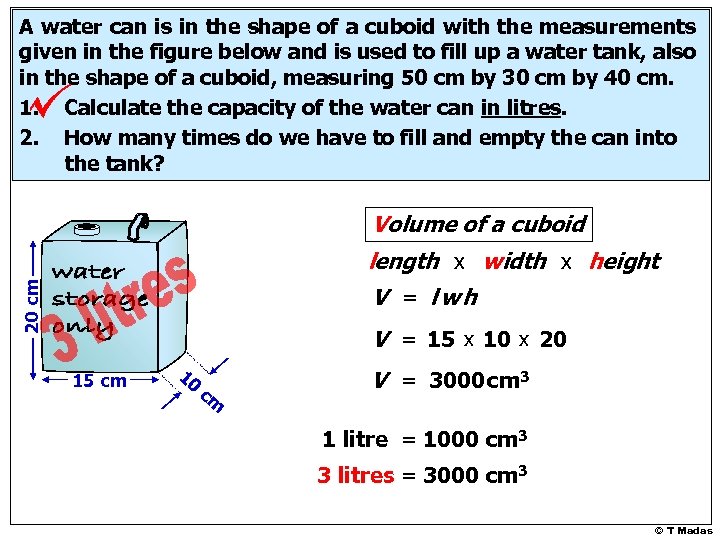 A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a water tank, also in the shape of a cuboid, measuring 50 cm by 30 cm by 40 cm. 1. Calculate the capacity of the water can in litres. 2. How many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 1 litre = 1000 cm 3 3 litres = 3000 cm 3 © T Madas
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a water tank, also in the shape of a cuboid, measuring 50 cm by 30 cm by 40 cm. 1. Calculate the capacity of the water can in litres. 2. How many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 1 litre = 1000 cm 3 3 litres = 3000 cm 3 © T Madas
 A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a water tank, also in the shape of a cuboid, measuring 50 cm by 30 cm by 40 cm. 1. Calculate the capacity of the water can in litres. 2. How many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 50 x 30 x 40 15 cm 10 We need to fill and empty the can 20 times cm V = 60000 cm 3 1 litre = 1000 cm 3 60 litres = 60000 cm 3 © T Madas
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a water tank, also in the shape of a cuboid, measuring 50 cm by 30 cm by 40 cm. 1. Calculate the capacity of the water can in litres. 2. How many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 50 x 30 x 40 15 cm 10 We need to fill and empty the can 20 times cm V = 60000 cm 3 1 litre = 1000 cm 3 60 litres = 60000 cm 3 © T Madas
 © T Madas
© T Madas
 A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? 2. 5 lengths in metres 4. 8 6. 2 The room has the shape of a cuboid. We must find the area of: The 4 walls The ceiling But not the floor! From the total we must subtract the area of the 2 windows and the door. Does it matter to this problem where the windows and the door are located? © T Madas
A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? 2. 5 lengths in metres 4. 8 6. 2 The room has the shape of a cuboid. We must find the area of: The 4 walls The ceiling But not the floor! From the total we must subtract the area of the 2 windows and the door. Does it matter to this problem where the windows and the door are located? © T Madas
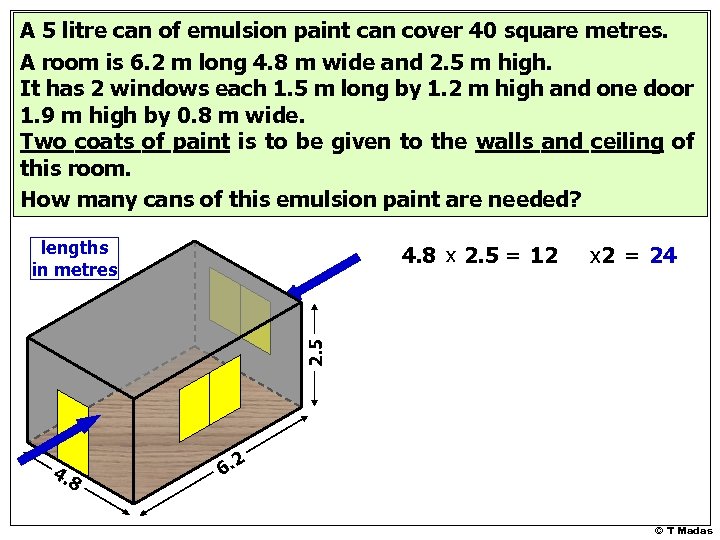 A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres x 2 = 24 2. 5 4. 8 x 2. 5 = 12 4. 8 6. 2 © T Madas
A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres x 2 = 24 2. 5 4. 8 x 2. 5 = 12 4. 8 6. 2 © T Madas
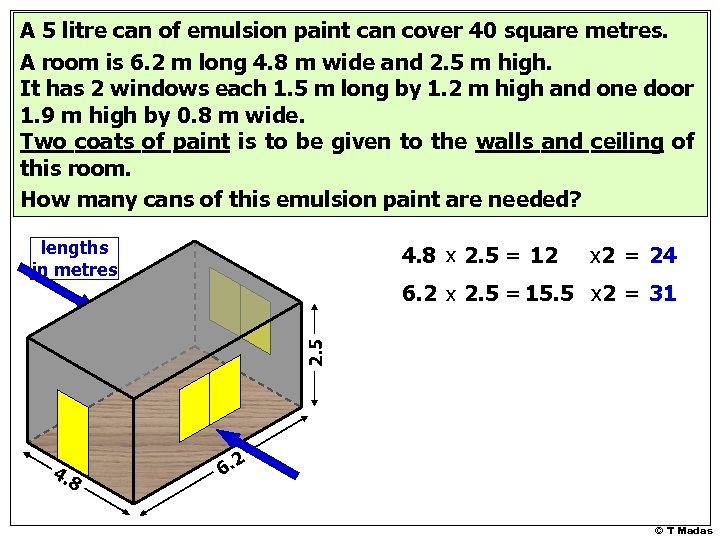 A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 4. 8 x 2. 5 = 12 x 2 = 24 2. 5 6. 2 x 2. 5 = 15. 5 x 2 = 31 4. 8 6. 2 © T Madas
A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 4. 8 x 2. 5 = 12 x 2 = 24 2. 5 6. 2 x 2. 5 = 15. 5 x 2 = 31 4. 8 6. 2 © T Madas
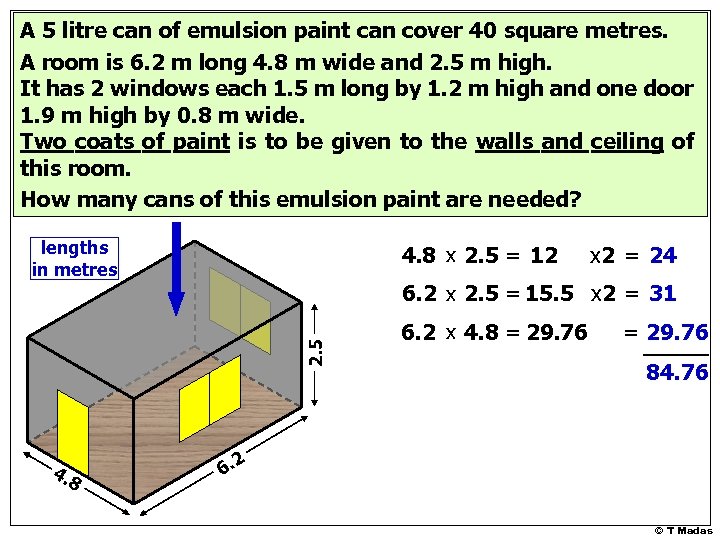 A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 4. 8 x 2. 5 = 12 6. 2 x 2. 5 = 15. 5 x 2 = 31 2. 5 4. 8 x 2 = 24 6. 2 x 4. 8 = 29. 76 84. 76 6. 2 © T Madas
A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 4. 8 x 2. 5 = 12 6. 2 x 2. 5 = 15. 5 x 2 = 31 2. 5 4. 8 x 2 = 24 6. 2 x 4. 8 = 29. 76 84. 76 6. 2 © T Madas
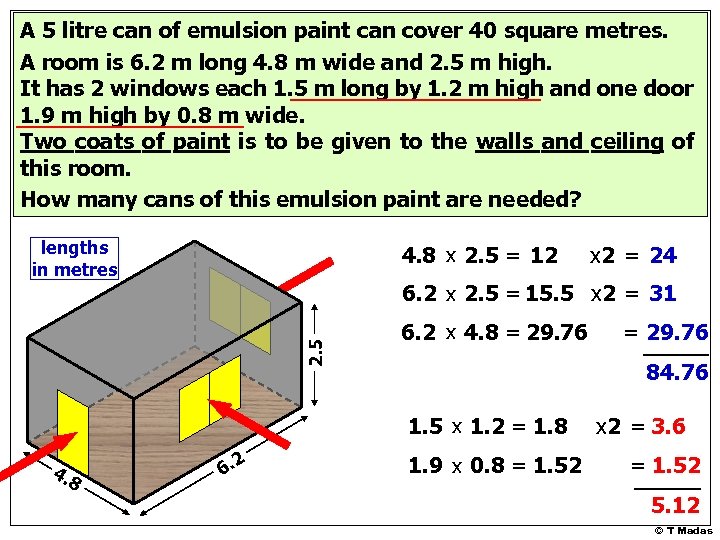 A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 4. 8 x 2. 5 = 12 2. 5 6. 2 x 2. 5 = 15. 5 x 2 = 31 6. 2 x 4. 8 = 29. 76 6. 2 = 29. 76 84. 76 1. 5 x 1. 2 = 1. 8 4. 8 x 2 = 24 1. 9 x 0. 8 = 1. 52 x 2 = 3. 6 = 1. 52 5. 12 © T Madas
A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 4. 8 x 2. 5 = 12 2. 5 6. 2 x 2. 5 = 15. 5 x 2 = 31 6. 2 x 4. 8 = 29. 76 6. 2 = 29. 76 84. 76 1. 5 x 1. 2 = 1. 8 4. 8 x 2 = 24 1. 9 x 0. 8 = 1. 52 x 2 = 3. 6 = 1. 52 5. 12 © T Madas
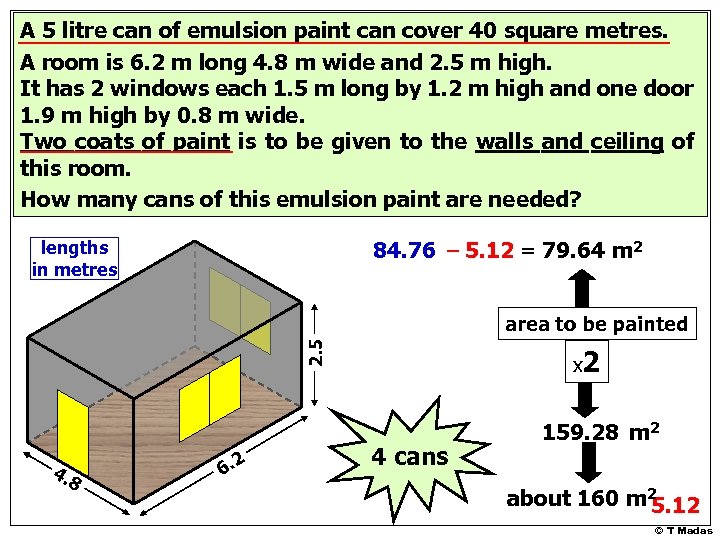 A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 84. 76 – 5. 12 = 79. 64 m 2 2. 5 area to be painted 4. 8 6. 2 x 2 4 cans 159. 28 m 2 about 160 m 2 5. 12 © T Madas
A 5 litre can of emulsion paint can cover 40 square metres. A room is 6. 2 m long 4. 8 m wide and 2. 5 m high. It has 2 windows each 1. 5 m long by 1. 2 m high and one door 1. 9 m high by 0. 8 m wide. Two coats of paint is to be given to the walls and ceiling of this room. How many cans of this emulsion paint are needed? lengths in metres 84. 76 – 5. 12 = 79. 64 m 2 2. 5 area to be painted 4. 8 6. 2 x 2 4 cans 159. 28 m 2 about 160 m 2 5. 12 © T Madas
 © T Madas
© T Madas
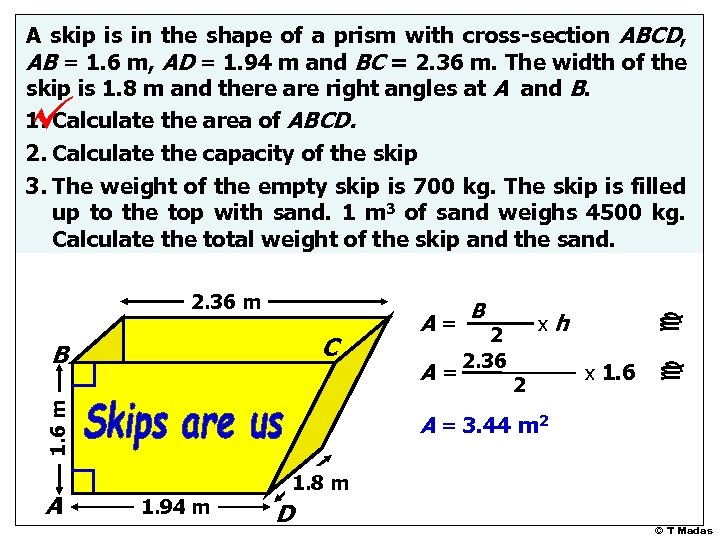 C 1. 6 m B A A= B+b xh 2 2. 36 + 1. 94 A= x 1. 6 2 c 2. 36 m c A skip is in the shape of a prism with cross-section ABCD, AB = 1. 6 m, AD = 1. 94 m and BC = 2. 36 m. The width of the skip is 1. 8 m and there are right angles at A and B. 1. Calculate the area of ABCD. 2. Calculate the capacity of the skip 3. The weight of the empty skip is 700 kg. The skip is filled up to the top with sand. 1 m 3 of sand weighs 4500 kg. Calculate the total weight of the skip and the sand. A = 3. 44 m 2 1. 94 m 1. 8 m D © T Madas
C 1. 6 m B A A= B+b xh 2 2. 36 + 1. 94 A= x 1. 6 2 c 2. 36 m c A skip is in the shape of a prism with cross-section ABCD, AB = 1. 6 m, AD = 1. 94 m and BC = 2. 36 m. The width of the skip is 1. 8 m and there are right angles at A and B. 1. Calculate the area of ABCD. 2. Calculate the capacity of the skip 3. The weight of the empty skip is 700 kg. The skip is filled up to the top with sand. 1 m 3 of sand weighs 4500 kg. Calculate the total weight of the skip and the sand. A = 3. 44 m 2 1. 94 m 1. 8 m D © T Madas
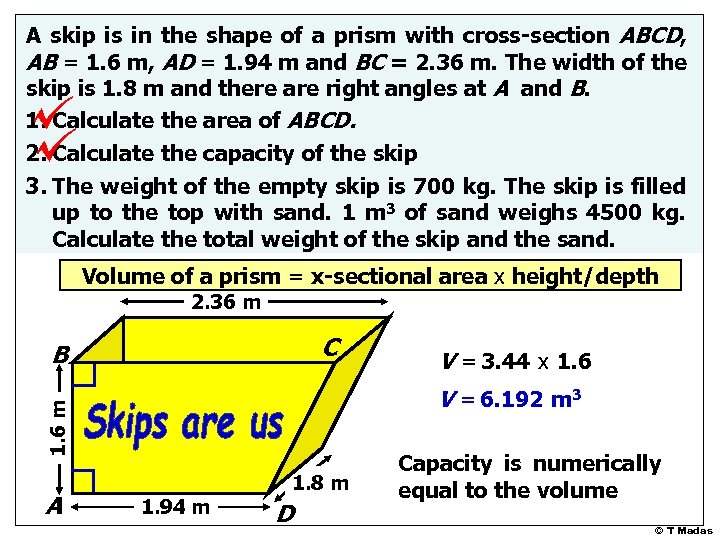 A skip is in the shape of a prism with cross-section ABCD, AB = 1. 6 m, AD = 1. 94 m and BC = 2. 36 m. The width of the skip is 1. 8 m and there are right angles at A and B. 1. Calculate the area of ABCD. 2. Calculate the capacity of the skip 3. The weight of the empty skip is 700 kg. The skip is filled up to the top with sand. 1 m 3 of sand weighs 4500 kg. Calculate the total weight of the skip and the sand. Volume of a prism = x-sectional area x height/depth 2. 36 m C B V = 6. 192 m 3 1. 6 m A V = 3. 44 x 1. 6 1. 94 m 1. 8 m D Capacity is numerically equal to the volume © T Madas
A skip is in the shape of a prism with cross-section ABCD, AB = 1. 6 m, AD = 1. 94 m and BC = 2. 36 m. The width of the skip is 1. 8 m and there are right angles at A and B. 1. Calculate the area of ABCD. 2. Calculate the capacity of the skip 3. The weight of the empty skip is 700 kg. The skip is filled up to the top with sand. 1 m 3 of sand weighs 4500 kg. Calculate the total weight of the skip and the sand. Volume of a prism = x-sectional area x height/depth 2. 36 m C B V = 6. 192 m 3 1. 6 m A V = 3. 44 x 1. 6 1. 94 m 1. 8 m D Capacity is numerically equal to the volume © T Madas
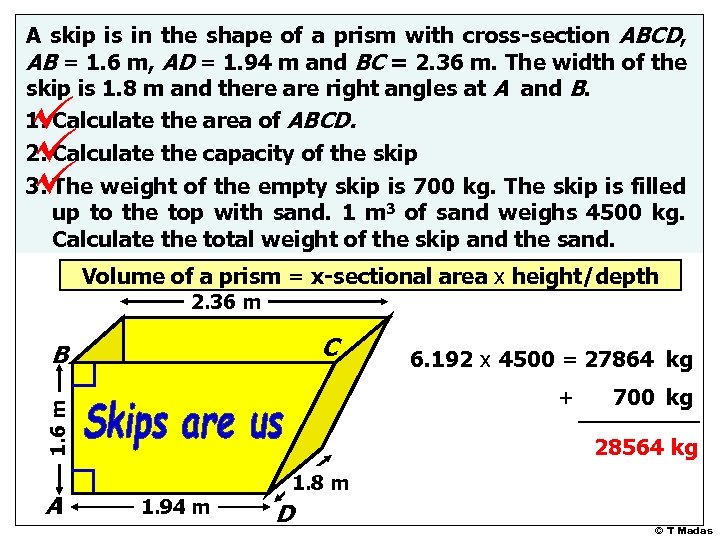 A skip is in the shape of a prism with cross-section ABCD, AB = 1. 6 m, AD = 1. 94 m and BC = 2. 36 m. The width of the skip is 1. 8 m and there are right angles at A and B. 1. Calculate the area of ABCD. 2. Calculate the capacity of the skip 3. The weight of the empty skip is 700 kg. The skip is filled up to the top with sand. 1 m 3 of sand weighs 4500 kg. Calculate the total weight of the skip and the sand. Volume of a prism = x-sectional area x height/depth 2. 36 m C B + 1. 6 m A 6. 192 x 4500 = 27864 kg 700 kg 28564 kg 1. 94 m 1. 8 m D © T Madas
A skip is in the shape of a prism with cross-section ABCD, AB = 1. 6 m, AD = 1. 94 m and BC = 2. 36 m. The width of the skip is 1. 8 m and there are right angles at A and B. 1. Calculate the area of ABCD. 2. Calculate the capacity of the skip 3. The weight of the empty skip is 700 kg. The skip is filled up to the top with sand. 1 m 3 of sand weighs 4500 kg. Calculate the total weight of the skip and the sand. Volume of a prism = x-sectional area x height/depth 2. 36 m C B + 1. 6 m A 6. 192 x 4500 = 27864 kg 700 kg 28564 kg 1. 94 m 1. 8 m D © T Madas
 © T Madas
© T Madas
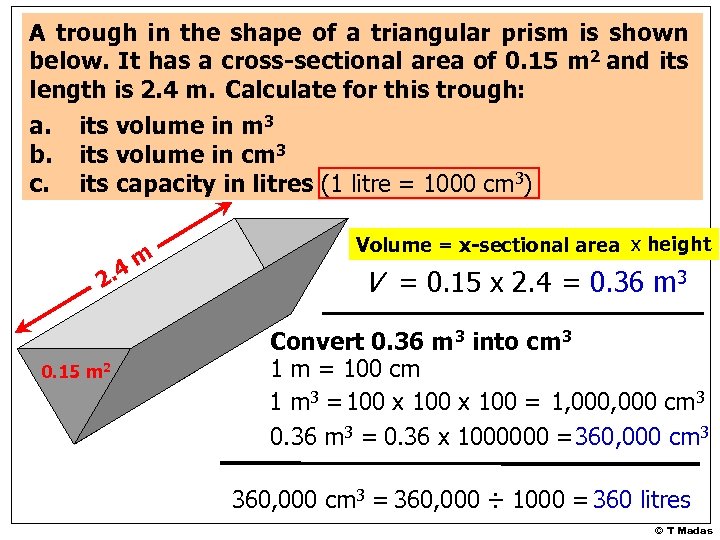 A trough in the shape of a triangular prism is shown below. It has a cross-sectional area of 0. 15 m 2 and its length is 2. 4 m. Calculate for this trough: a. its volume in m 3 b. its volume in cm 3 c. its capacity in litres (1 litre = 1000 cm 3) 4 m. 2 0. 15 m 2 Volume = x-sectional area x height V = 0. 15 x 2. 4 = 0. 36 m 3 Convert 0. 36 m 3 into cm 3 1 m = 100 cm 1 m 3 =100 x 100 = 1, 000 cm 3 0. 36 m 3 = 0. 36 x 1000000 =360, 000 cm 3 = 360, 000 ÷ 1000 = 360 litres © T Madas
A trough in the shape of a triangular prism is shown below. It has a cross-sectional area of 0. 15 m 2 and its length is 2. 4 m. Calculate for this trough: a. its volume in m 3 b. its volume in cm 3 c. its capacity in litres (1 litre = 1000 cm 3) 4 m. 2 0. 15 m 2 Volume = x-sectional area x height V = 0. 15 x 2. 4 = 0. 36 m 3 Convert 0. 36 m 3 into cm 3 1 m = 100 cm 1 m 3 =100 x 100 = 1, 000 cm 3 0. 36 m 3 = 0. 36 x 1000000 =360, 000 cm 3 = 360, 000 ÷ 1000 = 360 litres © T Madas
 © T Madas
© T Madas
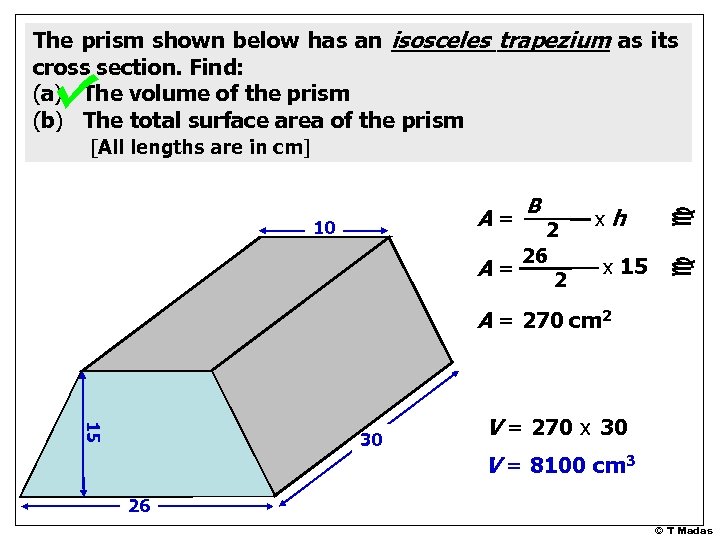 The prism shown below has an isosceles trapezium as its cross section. Find: (a) The volume of the prism (b) The total surface area of the prism B+b xh 2 26 + 10 x 15 A= 2 10 c A= c [All lengths are in cm] A = 270 cm 2 15 30 V = 270 x 30 V = 8100 cm 3 26 © T Madas
The prism shown below has an isosceles trapezium as its cross section. Find: (a) The volume of the prism (b) The total surface area of the prism B+b xh 2 26 + 10 x 15 A= 2 10 c A= c [All lengths are in cm] A = 270 cm 2 15 30 V = 270 x 30 V = 8100 cm 3 26 © T Madas
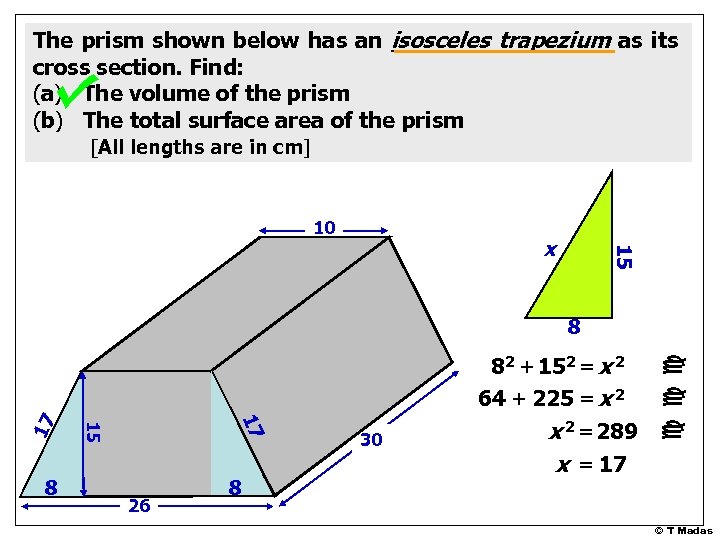 The prism shown below has an isosceles trapezium as its cross section. Find: (a) The volume of the prism (b) The total surface area of the prism [All lengths are in cm] 10 15 x 26 8 30 82 + 152 = x 2 64 + 225 = x 2 = 289 c c c 17 8 15 17 8 x = 17 © T Madas
The prism shown below has an isosceles trapezium as its cross section. Find: (a) The volume of the prism (b) The total surface area of the prism [All lengths are in cm] 10 15 x 26 8 30 82 + 152 = x 2 64 + 225 = x 2 = 289 c c c 17 8 15 17 8 x = 17 © T Madas
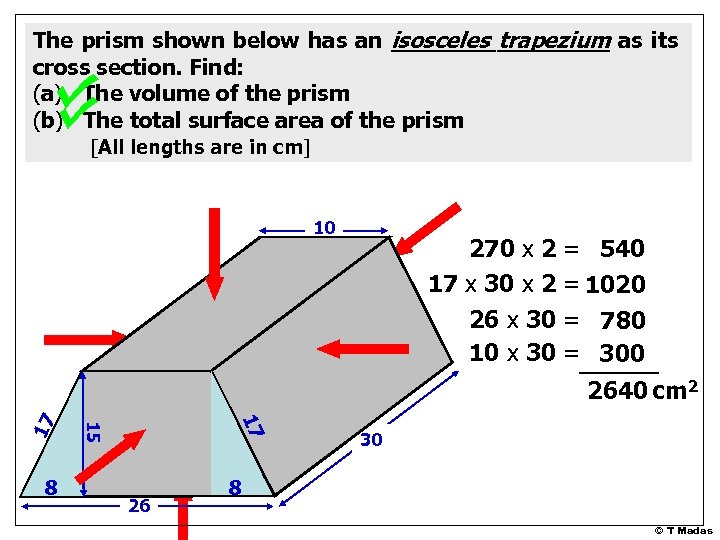 The prism shown below has an isosceles trapezium as its cross section. Find: (a) The volume of the prism (b) The total surface area of the prism [All lengths are in cm] 10 270 x 2 = 540 17 x 30 x 2 = 1020 26 x 30 = 780 10 x 30 = 300 17 8 15 17 2640 cm 2 26 30 8 © T Madas
The prism shown below has an isosceles trapezium as its cross section. Find: (a) The volume of the prism (b) The total surface area of the prism [All lengths are in cm] 10 270 x 2 = 540 17 x 30 x 2 = 1020 26 x 30 = 780 10 x 30 = 300 17 8 15 17 2640 cm 2 26 30 8 © T Madas
 © T Madas
© T Madas
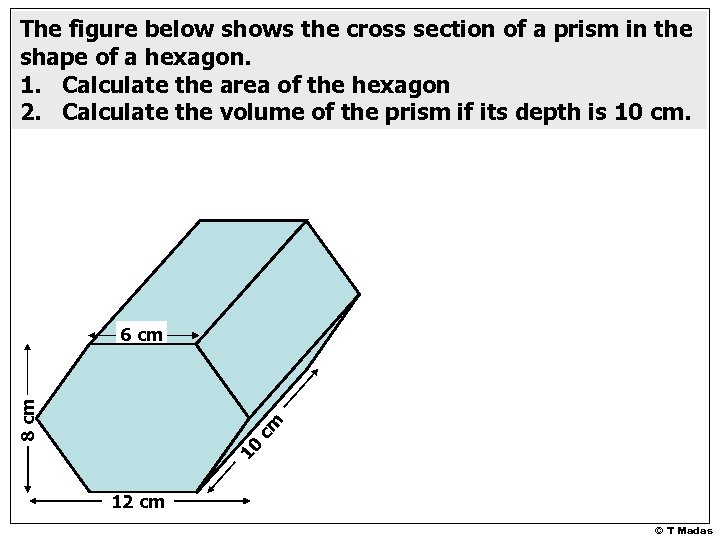 The figure below shows the cross section of a prism in the shape of a hexagon. 1. Calculate the area of the hexagon 2. Calculate the volume of the prism if its depth is 10 cm 8 cm 6 cm 12 cm © T Madas
The figure below shows the cross section of a prism in the shape of a hexagon. 1. Calculate the area of the hexagon 2. Calculate the volume of the prism if its depth is 10 cm 8 cm 6 cm 12 cm © T Madas
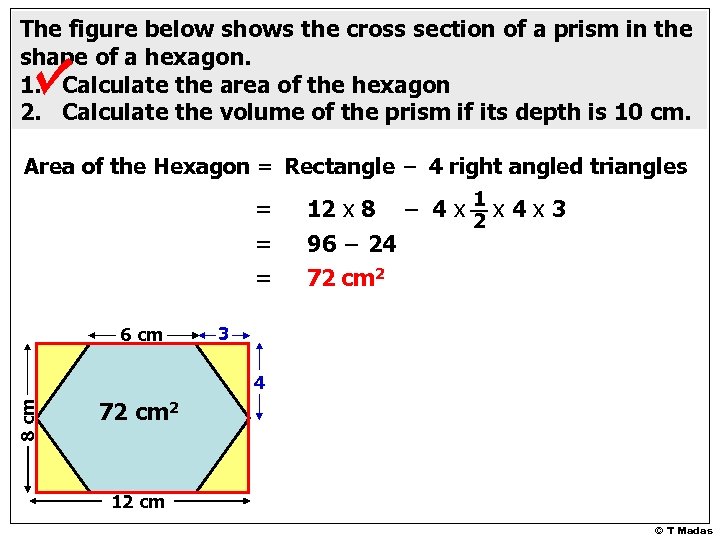 The figure below shows the cross section of a prism in the shape of a hexagon. 1. Calculate the area of the hexagon 2. Calculate the volume of the prism if its depth is 10 cm. Area of the Hexagon = Rectangle – 4 right angled triangles = = = 6 cm 12 x 8 – 4 x 1 x 4 x 3 2 96 – 24 72 cm 2 3 8 cm 4 72 cm 2 12 cm © T Madas
The figure below shows the cross section of a prism in the shape of a hexagon. 1. Calculate the area of the hexagon 2. Calculate the volume of the prism if its depth is 10 cm. Area of the Hexagon = Rectangle – 4 right angled triangles = = = 6 cm 12 x 8 – 4 x 1 x 4 x 3 2 96 – 24 72 cm 2 3 8 cm 4 72 cm 2 12 cm © T Madas
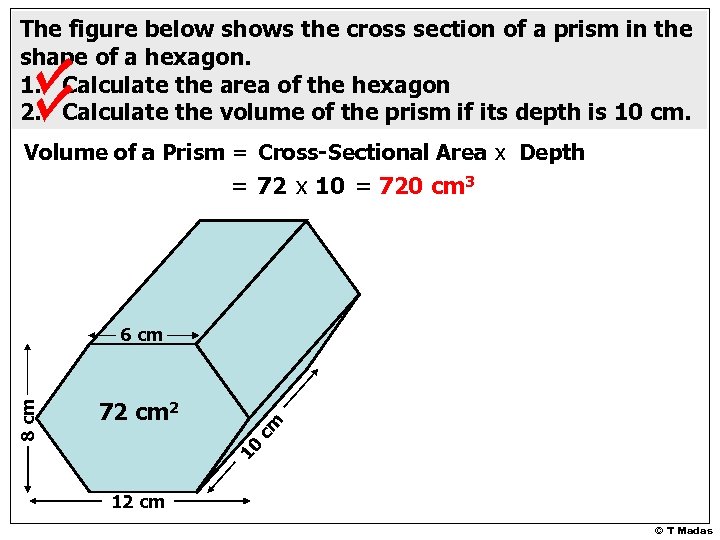 The figure below shows the cross section of a prism in the shape of a hexagon. 1. Calculate the area of the hexagon 2. Calculate the volume of the prism if its depth is 10 cm. Volume of a Prism = Cross-Sectional Area x Depth = 72 x 10 = 720 cm 3 cm 72 cm 2 10 8 cm 6 cm 12 cm © T Madas
The figure below shows the cross section of a prism in the shape of a hexagon. 1. Calculate the area of the hexagon 2. Calculate the volume of the prism if its depth is 10 cm. Volume of a Prism = Cross-Sectional Area x Depth = 72 x 10 = 720 cm 3 cm 72 cm 2 10 8 cm 6 cm 12 cm © T Madas
 © T Madas
© T Madas
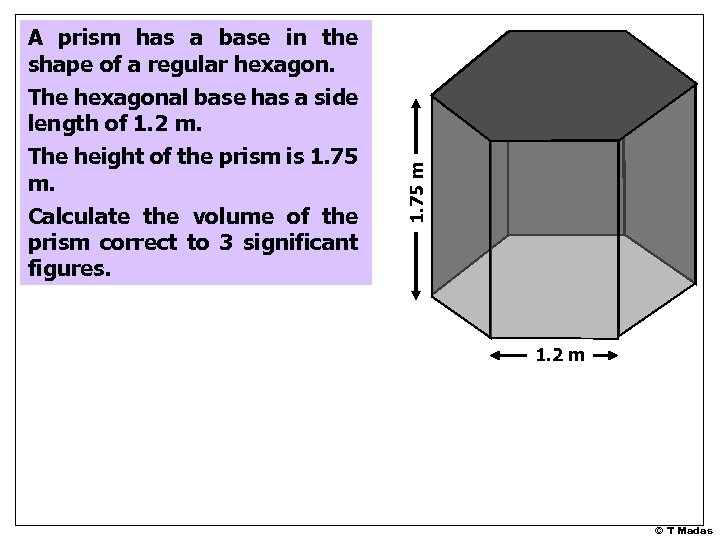 The height of the prism is 1. 75 m. Calculate the volume of the prism correct to 3 significant figures. 1. 75 m A prism has a base in the shape of a regular hexagon. The hexagonal base has a side length of 1. 2 m © T Madas
The height of the prism is 1. 75 m. Calculate the volume of the prism correct to 3 significant figures. 1. 75 m A prism has a base in the shape of a regular hexagon. The hexagonal base has a side length of 1. 2 m © T Madas
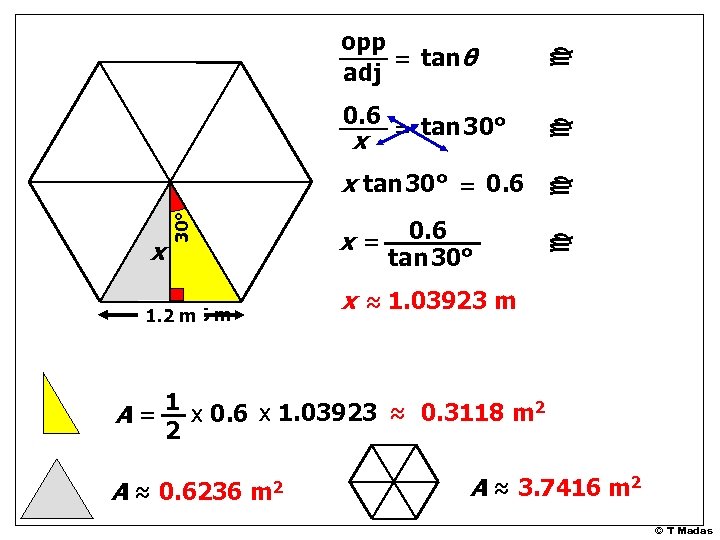 0. 6 1. 2 m m c c x 30° x tan 30° = 0. 6 tan 30° c x = tan 30° c opp = tanθ adj x= x ≈ 1. 03923 m A = 1 x 0. 6 x 1. 03923 ≈ 0. 3118 m 2 2 A ≈ 0. 6236 m 2 A ≈ 3. 7416 m 2 © T Madas
0. 6 1. 2 m m c c x 30° x tan 30° = 0. 6 tan 30° c x = tan 30° c opp = tanθ adj x= x ≈ 1. 03923 m A = 1 x 0. 6 x 1. 03923 ≈ 0. 3118 m 2 2 A ≈ 0. 6236 m 2 A ≈ 3. 7416 m 2 © T Madas
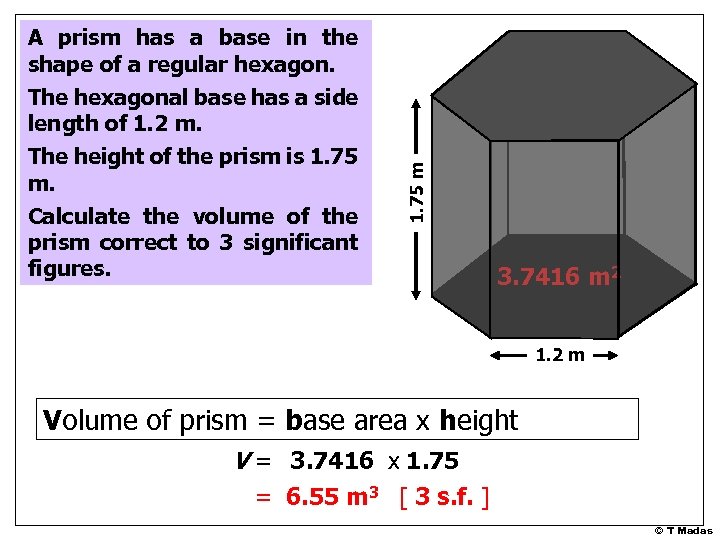 The height of the prism is 1. 75 m. Calculate the volume of the prism correct to 3 significant figures. 1. 75 m A prism has a base in the shape of a regular hexagon. The hexagonal base has a side length of 1. 2 m. 3. 7416 m 2 1. 2 m Volume of prism = base area x height V = 3. 7416 x 1. 75 = 6. 55 m 3 [ 3 s. f. ] © T Madas
The height of the prism is 1. 75 m. Calculate the volume of the prism correct to 3 significant figures. 1. 75 m A prism has a base in the shape of a regular hexagon. The hexagonal base has a side length of 1. 2 m. 3. 7416 m 2 1. 2 m Volume of prism = base area x height V = 3. 7416 x 1. 75 = 6. 55 m 3 [ 3 s. f. ] © T Madas
 © T Madas
© T Madas
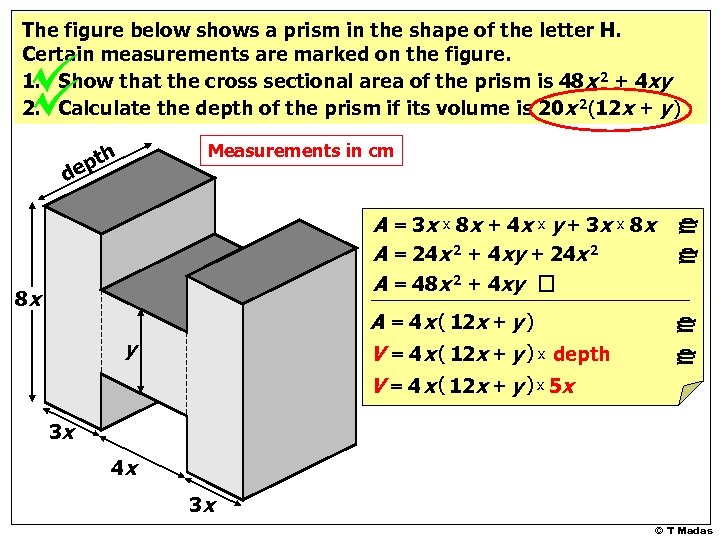 The figure below shows a prism in the shape of the letter H. Certain measurements are marked on the figure. 1. Show that the cross sectional area of the prism is 48 x 2 + 4 xy 2. Calculate the depth of the prism if its volume is 20 x 2(12 x + y ) Measurements in cm pth e 8 x A = 4 x ( 12 x + y ) V = 4 x ( 12 x + y ) x depth V = 4 x ( 12 x + y ) x 5 x y c c A = 3 x x 8 x + 4 x x y + 3 x x 8 x A = 24 x 2 + 4 xy + 24 x 2 A = 48 x 2 + 4 xy c c d 3 x 4 x 3 x © T Madas
The figure below shows a prism in the shape of the letter H. Certain measurements are marked on the figure. 1. Show that the cross sectional area of the prism is 48 x 2 + 4 xy 2. Calculate the depth of the prism if its volume is 20 x 2(12 x + y ) Measurements in cm pth e 8 x A = 4 x ( 12 x + y ) V = 4 x ( 12 x + y ) x depth V = 4 x ( 12 x + y ) x 5 x y c c A = 3 x x 8 x + 4 x x y + 3 x x 8 x A = 24 x 2 + 4 xy + 24 x 2 A = 48 x 2 + 4 xy c c d 3 x 4 x 3 x © T Madas
 © T Madas
© T Madas
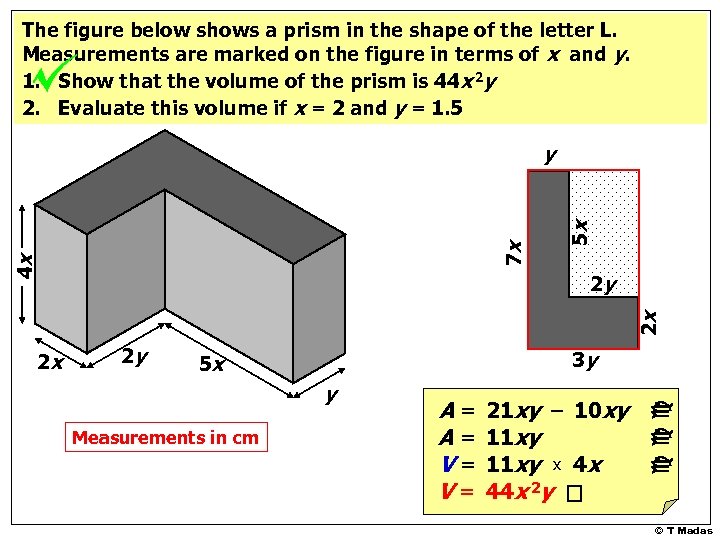 The figure below shows a prism in the shape of the letter L. Measurements are marked on the figure in terms of x and y. 1. Show that the volume of the prism is 44 x 2 y 2. Evaluate this volume if x = 2 and y = 1. 5 4 x 5 x 7 x y 2 x 2 y 2 y 3 y 5 x y Measurements in cm A= A= V= V= 21 xy – 10 xy 11 xy x 4 x 44 x 2 y ccc 2 x © T Madas
The figure below shows a prism in the shape of the letter L. Measurements are marked on the figure in terms of x and y. 1. Show that the volume of the prism is 44 x 2 y 2. Evaluate this volume if x = 2 and y = 1. 5 4 x 5 x 7 x y 2 x 2 y 2 y 3 y 5 x y Measurements in cm A= A= V= V= 21 xy – 10 xy 11 xy x 4 x 44 x 2 y ccc 2 x © T Madas
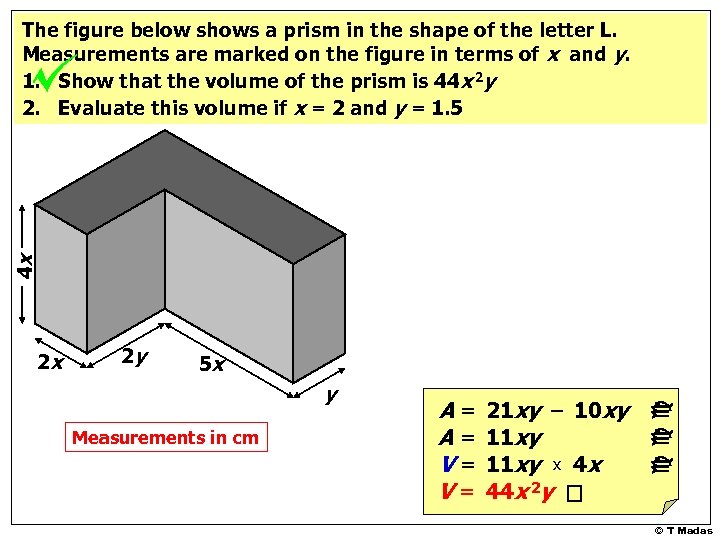 4 x The figure below shows a prism in the shape of the letter L. Measurements are marked on the figure in terms of x and y. 1. Show that the volume of the prism is 44 x 2 y 2. Evaluate this volume if x = 2 and y = 1. 5 2 y 5 x y Measurements in cm A= A= V= V= 21 xy – 10 xy 11 xy x 4 x 44 x 2 y ccc 2 x © T Madas
4 x The figure below shows a prism in the shape of the letter L. Measurements are marked on the figure in terms of x and y. 1. Show that the volume of the prism is 44 x 2 y 2. Evaluate this volume if x = 2 and y = 1. 5 2 y 5 x y Measurements in cm A= A= V= V= 21 xy – 10 xy 11 xy x 4 x 44 x 2 y ccc 2 x © T Madas
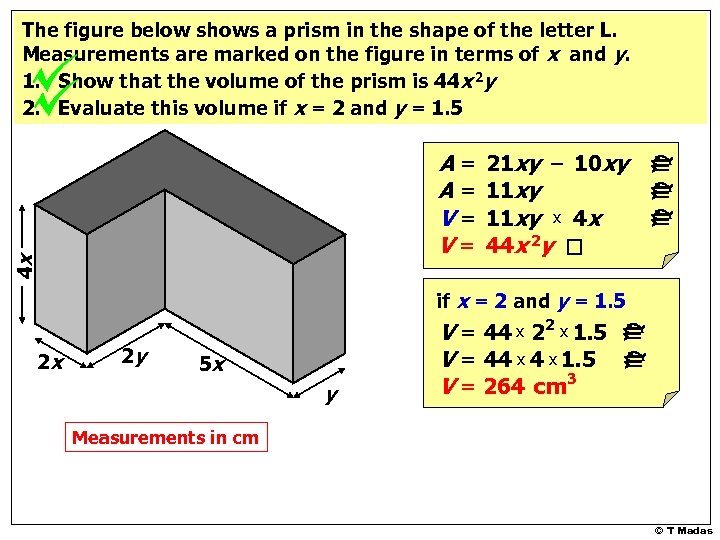 4 x A= A= V= V= 21 xy – 10 xy 11 xy x 4 x 44 x 2 y ccc The figure below shows a prism in the shape of the letter L. Measurements are marked on the figure in terms of x and y. 1. Show that the volume of the prism is 44 x 2 y 2. Evaluate this volume if x = 2 and y = 1. 5 2 x 2 y 5 x y V = 44 x 22 x 1. 5 V = 44 x 1. 5 V = 264 cm 3 cc if x = 2 and y = 1. 5 Measurements in cm © T Madas
4 x A= A= V= V= 21 xy – 10 xy 11 xy x 4 x 44 x 2 y ccc The figure below shows a prism in the shape of the letter L. Measurements are marked on the figure in terms of x and y. 1. Show that the volume of the prism is 44 x 2 y 2. Evaluate this volume if x = 2 and y = 1. 5 2 x 2 y 5 x y V = 44 x 22 x 1. 5 V = 44 x 1. 5 V = 264 cm 3 cc if x = 2 and y = 1. 5 Measurements in cm © T Madas
 Exam Question © T Madas
Exam Question © T Madas
 An ice hockey puck can be modelled as a cylinder of radius 4. 2 cm and a thickness of 3. 2 cm. The puck is made out of rubber material with a density of 1. 35 grams per cm 3. Calculate to 3 significant figures: (a) The volume of the puck in cm 3 (b) The mass of the puck in grams 4. 2 cm 3. 2 cm V = π r 2 h V = π x 4. 22 x 3. 2 V ≈ 177. 337 cm 3 V ≈ 177 cm 3 [3 s. f. ] Density of 1. 35 grams per cm 3 means that there is a mass of 1. 35 grams for every cm 3 of volume: Mass = 177. 337 x 1. 35 ≈ 239. 404 = 239 grams (3 s. f. ) © T Madas
An ice hockey puck can be modelled as a cylinder of radius 4. 2 cm and a thickness of 3. 2 cm. The puck is made out of rubber material with a density of 1. 35 grams per cm 3. Calculate to 3 significant figures: (a) The volume of the puck in cm 3 (b) The mass of the puck in grams 4. 2 cm 3. 2 cm V = π r 2 h V = π x 4. 22 x 3. 2 V ≈ 177. 337 cm 3 V ≈ 177 cm 3 [3 s. f. ] Density of 1. 35 grams per cm 3 means that there is a mass of 1. 35 grams for every cm 3 of volume: Mass = 177. 337 x 1. 35 ≈ 239. 404 = 239 grams (3 s. f. ) © T Madas
 © T Madas
© T Madas
 A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 © T Madas
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 © T Madas
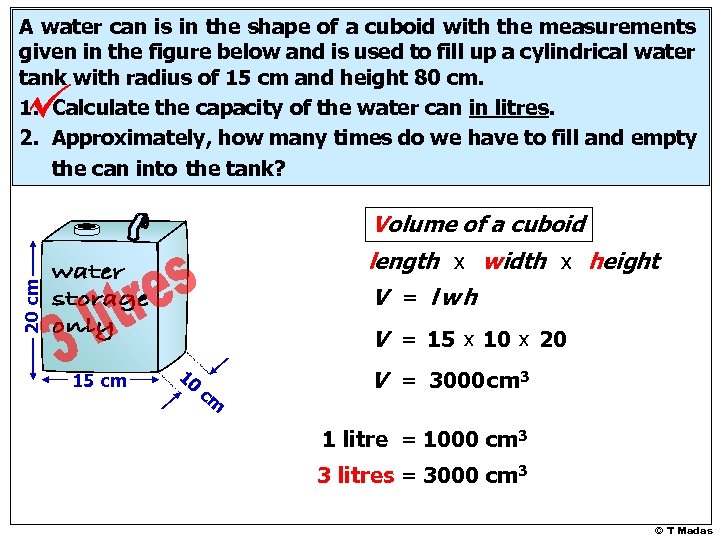 A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 1 litre = 1000 cm 3 3 litres = 3000 cm 3 © T Madas
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 1 litre = 1000 cm 3 3 litres = 3000 cm 3 © T Madas
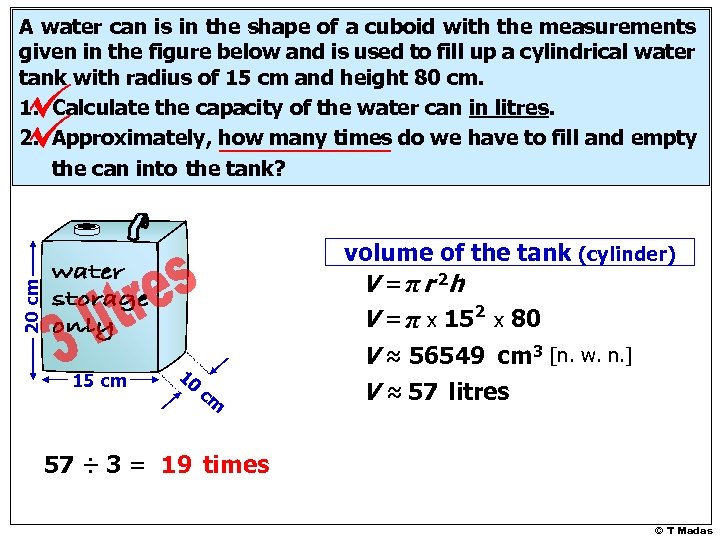 A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? 20 cm volume of the tank (cylinder) V = π r 2 h V = π x 152 x 80 15 cm 10 cm V ≈ 56549 cm 3 [n. w. n. ] V ≈ 57 litres 57 ÷ 3 = 19 times © T Madas
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? 20 cm volume of the tank (cylinder) V = π r 2 h V = π x 152 x 80 15 cm 10 cm V ≈ 56549 cm 3 [n. w. n. ] V ≈ 57 litres 57 ÷ 3 = 19 times © T Madas
 © T Madas
© T Madas
 A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness is measured as 7 ± 0. 5 mm. Calculate to 3 significant figures: 1. the maximum possible volume of the biscuit in cm 3. 2. the minimum possible surface area of this biscuit in cm 2. 70 ± 1 mm V = π r 2 h V = π x 35. 52 x 7. 5 V ≈ 29694 mm 3 V ≈ 29. 7 cm 3 [3 s. f. ] 7 ± 0. 5 mm 1 cm 3 = 1000 mm 3 © T Madas
A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness is measured as 7 ± 0. 5 mm. Calculate to 3 significant figures: 1. the maximum possible volume of the biscuit in cm 3. 2. the minimum possible surface area of this biscuit in cm 2. 70 ± 1 mm V = π r 2 h V = π x 35. 52 x 7. 5 V ≈ 29694 mm 3 V ≈ 29. 7 cm 3 [3 s. f. ] 7 ± 0. 5 mm 1 cm 3 = 1000 mm 3 © T Madas
 A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness is measured as 7 ± 0. 5 mm. Calculate to 3 significant figures: 1. the maximum possible volume of the biscuit in cm 3. 2. the minimum possible surface area of this biscuit in cm 2. 70 ± 1 mm 7 ± 0. 5 mm A = π r 2 + 2π r h A=π x 34. 52 + 2 x π x 34. 5 x 6. 5 A ≈ 8888 mm 2 V ≈ 88. 9 cm 2 [3 s. f. ] 1 cm 2 = 100 mm 2 © T Madas
A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness is measured as 7 ± 0. 5 mm. Calculate to 3 significant figures: 1. the maximum possible volume of the biscuit in cm 3. 2. the minimum possible surface area of this biscuit in cm 2. 70 ± 1 mm 7 ± 0. 5 mm A = π r 2 + 2π r h A=π x 34. 52 + 2 x π x 34. 5 x 6. 5 A ≈ 8888 mm 2 V ≈ 88. 9 cm 2 [3 s. f. ] 1 cm 2 = 100 mm 2 © T Madas
 © T Madas
© T Madas
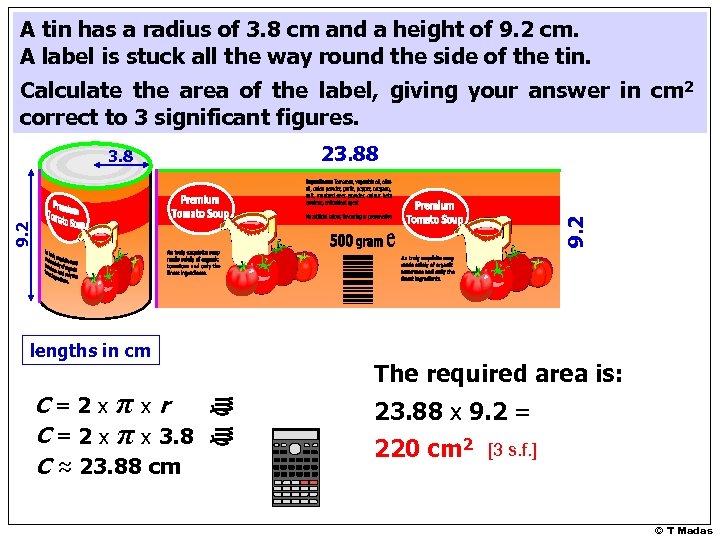 A tin has a radius of 3. 8 cm and a height of 9. 2 cm. A label is stuck all the way round the side of the tin. Calculate the area of the label, giving your answer in cm 2 correct to 3 significant figures. 23. 88 9. 2 3. 8 lengths in cm cc C=2 x πx r C = 2 x π x 3. 8 C ≈ 23. 88 cm The required area is: 23. 88 x 9. 2 = 220 cm 2 [3 s. f. ] © T Madas
A tin has a radius of 3. 8 cm and a height of 9. 2 cm. A label is stuck all the way round the side of the tin. Calculate the area of the label, giving your answer in cm 2 correct to 3 significant figures. 23. 88 9. 2 3. 8 lengths in cm cc C=2 x πx r C = 2 x π x 3. 8 C ≈ 23. 88 cm The required area is: 23. 88 x 9. 2 = 220 cm 2 [3 s. f. ] © T Madas
 © T Madas
© T Madas
 A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. cm V = 50π x 45 20 cm V = 2250 π c 45 2 π x 102 x 45 V= 2 c c V= πx r 2 x h c Volume = x - sectional area x length (height) V = 7070 cm 3 [3 s. f. ] © T Madas
A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. cm V = 50π x 45 20 cm V = 2250 π c 45 2 π x 102 x 45 V= 2 c c V= πx r 2 x h c Volume = x - sectional area x length (height) V = 7070 cm 3 [3 s. f. ] © T Madas
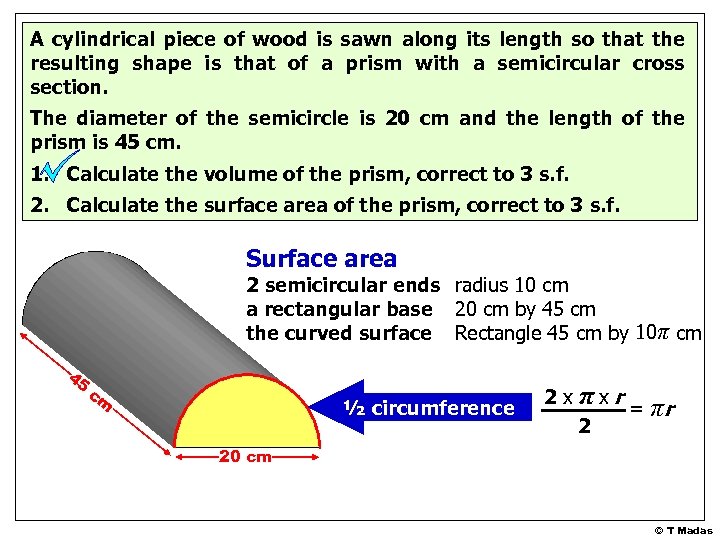 A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. Surface area 2 semicircular ends radius 10 cm a rectangular base 20 cm by 45 cm ? the curved surface Rectangle 45 cm by 10π cm 45 cm ½ circumference 2 x πx r = πr 2 20 cm © T Madas
A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. Surface area 2 semicircular ends radius 10 cm a rectangular base 20 cm by 45 cm ? the curved surface Rectangle 45 cm by 10π cm 45 cm ½ circumference 2 x πx r = πr 2 20 cm © T Madas
 A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. Surface area 2 semicircular ends radius 10 cm a rectangular base 20 cm by 45 cm ? the curved surface Rectangle 45 cm by 10π cm 45 π cm 20 cm x 102 = 100π 20 x 45 = 900 45 x 10π = 450π 900 + 550π 2630 cm 2 [3 s. f. ] © T Madas
A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. Surface area 2 semicircular ends radius 10 cm a rectangular base 20 cm by 45 cm ? the curved surface Rectangle 45 cm by 10π cm 45 π cm 20 cm x 102 = 100π 20 x 45 = 900 45 x 10π = 450π 900 + 550π 2630 cm 2 [3 s. f. ] © T Madas
 Exam Question © T Madas
Exam Question © T Madas
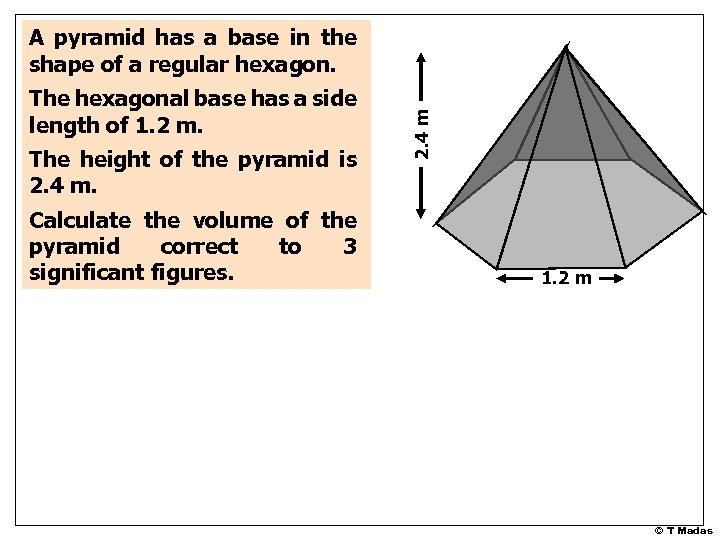 The hexagonal base has a side length of 1. 2 m. The height of the pyramid is 2. 4 m. Calculate the volume of the pyramid correct to 3 significant figures. 2. 4 m A pyramid has a base in the shape of a regular hexagon. 1. 2 m © T Madas
The hexagonal base has a side length of 1. 2 m. The height of the pyramid is 2. 4 m. Calculate the volume of the pyramid correct to 3 significant figures. 2. 4 m A pyramid has a base in the shape of a regular hexagon. 1. 2 m © T Madas
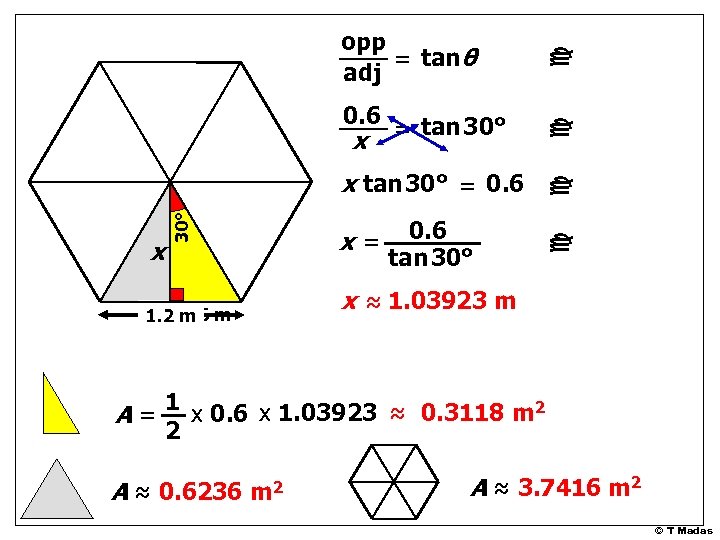 0. 6 1. 2 m m c c x 30° x tan 30° = 0. 6 tan 30° c x = tan 30° c opp = tanθ adj x= x ≈ 1. 03923 m A = 1 x 0. 6 x 1. 03923 ≈ 0. 3118 m 2 2 A ≈ 0. 6236 m 2 A ≈ 3. 7416 m 2 © T Madas
0. 6 1. 2 m m c c x 30° x tan 30° = 0. 6 tan 30° c x = tan 30° c opp = tanθ adj x= x ≈ 1. 03923 m A = 1 x 0. 6 x 1. 03923 ≈ 0. 3118 m 2 2 A ≈ 0. 6236 m 2 A ≈ 3. 7416 m 2 © T Madas
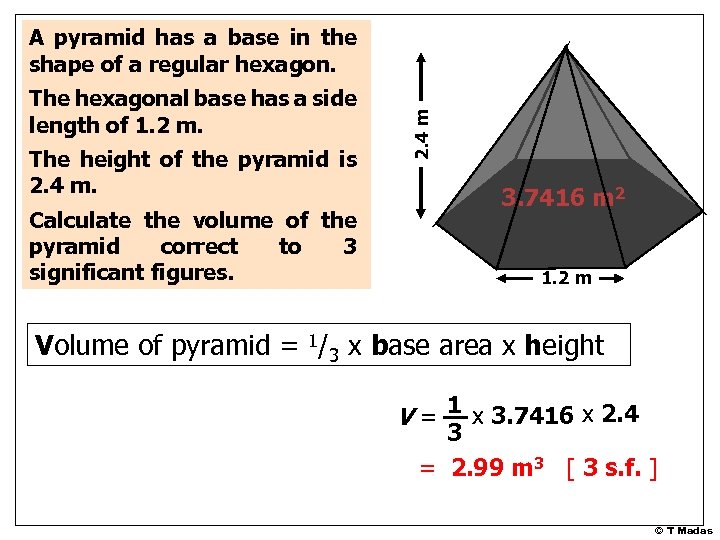 The hexagonal base has a side length of 1. 2 m. The height of the pyramid is 2. 4 m. Calculate the volume of the pyramid correct to 3 significant figures. 2. 4 m A pyramid has a base in the shape of a regular hexagon. 3. 7416 m 2 1. 2 m Volume of pyramid = 1/3 x base area x height V = 1 x 3. 7416 x 2. 4 3 = 2. 99 m 3 [ 3 s. f. ] © T Madas
The hexagonal base has a side length of 1. 2 m. The height of the pyramid is 2. 4 m. Calculate the volume of the pyramid correct to 3 significant figures. 2. 4 m A pyramid has a base in the shape of a regular hexagon. 3. 7416 m 2 1. 2 m Volume of pyramid = 1/3 x base area x height V = 1 x 3. 7416 x 2. 4 3 = 2. 99 m 3 [ 3 s. f. ] © T Madas
 Exam Question © T Madas
Exam Question © T Madas
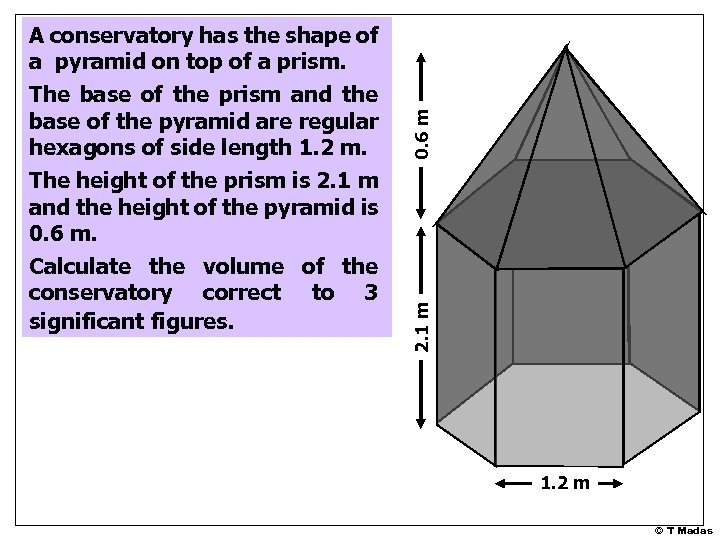 0. 6 m 2. 1 m A conservatory has the shape of a pyramid on top of a prism. The base of the prism and the base of the pyramid are regular hexagons of side length 1. 2 m. The height of the prism is 2. 1 m and the height of the pyramid is 0. 6 m. Calculate the volume of the conservatory correct to 3 significant figures. 1. 2 m © T Madas
0. 6 m 2. 1 m A conservatory has the shape of a pyramid on top of a prism. The base of the prism and the base of the pyramid are regular hexagons of side length 1. 2 m. The height of the prism is 2. 1 m and the height of the pyramid is 0. 6 m. Calculate the volume of the conservatory correct to 3 significant figures. 1. 2 m © T Madas
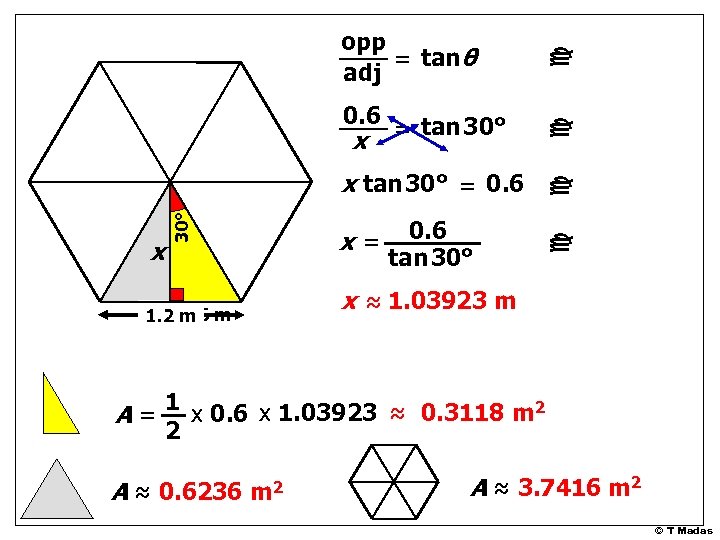 0. 6 1. 2 m m c c x 30° x tan 30° = 0. 6 tan 30° c x = tan 30° c opp = tanθ adj x= x ≈ 1. 03923 m A = 1 x 0. 6 x 1. 03923 ≈ 0. 3118 m 2 2 A ≈ 0. 6236 m 2 A ≈ 3. 7416 m 2 © T Madas
0. 6 1. 2 m m c c x 30° x tan 30° = 0. 6 tan 30° c x = tan 30° c opp = tanθ adj x= x ≈ 1. 03923 m A = 1 x 0. 6 x 1. 03923 ≈ 0. 3118 m 2 2 A ≈ 0. 6236 m 2 A ≈ 3. 7416 m 2 © T Madas
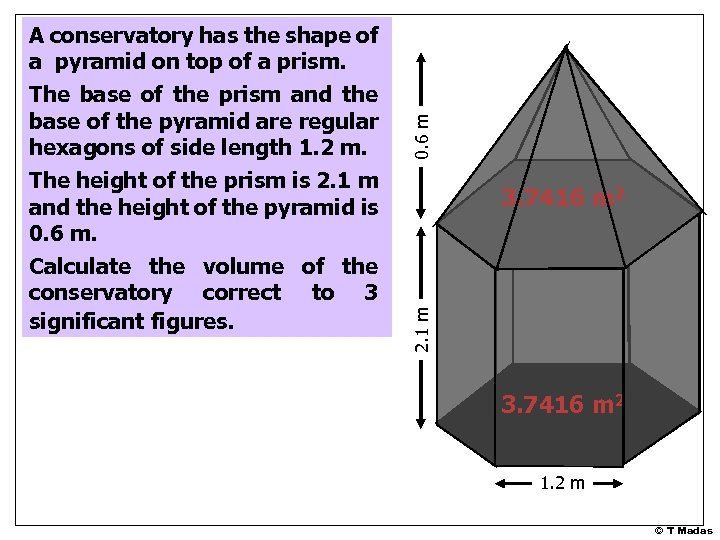 0. 6 m 3. 7416 m 2 2. 1 m A conservatory has the shape of a pyramid on top of a prism. The base of the prism and the base of the pyramid are regular hexagons of side length 1. 2 m. The height of the prism is 2. 1 m and the height of the pyramid is 0. 6 m. Calculate the volume of the conservatory correct to 3 significant figures. 3. 7416 m 2 1. 2 m © T Madas
0. 6 m 3. 7416 m 2 2. 1 m A conservatory has the shape of a pyramid on top of a prism. The base of the prism and the base of the pyramid are regular hexagons of side length 1. 2 m. The height of the prism is 2. 1 m and the height of the pyramid is 0. 6 m. Calculate the volume of the conservatory correct to 3 significant figures. 3. 7416 m 2 1. 2 m © T Madas
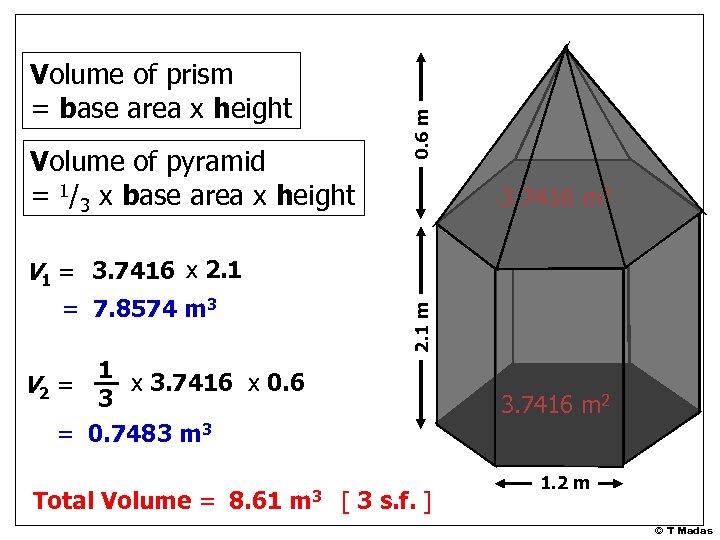 Volume of pyramid = 1/3 x base area x height 0. 6 m Volume of prism = base area x height 3. 7416 m 2 V 1 = 3. 7416 x 2. 1 m = 7. 8574 m 3 1 x 3. 7416 x 0. 6 V 2 = 3 = 0. 7483 m 3 Total Volume = 8. 61 m 3 3. 7416 m 2 [ 3 s. f. ] 1. 2 m © T Madas
Volume of pyramid = 1/3 x base area x height 0. 6 m Volume of prism = base area x height 3. 7416 m 2 V 1 = 3. 7416 x 2. 1 m = 7. 8574 m 3 1 x 3. 7416 x 0. 6 V 2 = 3 = 0. 7483 m 3 Total Volume = 8. 61 m 3 3. 7416 m 2 [ 3 s. f. ] 1. 2 m © T Madas
 © T Madas
© T Madas
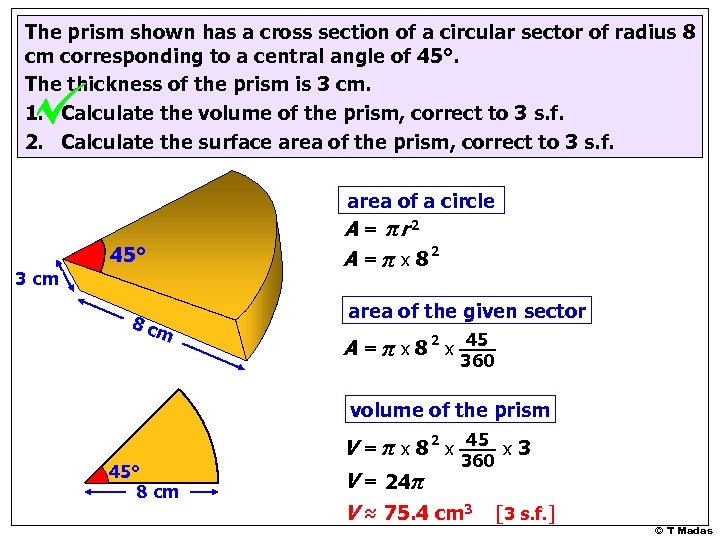 The prism shown has a cross section of a circular sector of radius 8 cm corresponding to a central angle of 45°. The thickness of the prism is 3 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. area of a circle A = πr 2 A = π x 82 45° 3 cm 8 c m area of the given sector A = π x 8 2 x 45 360 volume of the prism 45° 8 cm V = π x 8 2 x 45 x 3 360 V = 24π V ≈ 75. 4 cm 3 [3 s. f. ] © T Madas
The prism shown has a cross section of a circular sector of radius 8 cm corresponding to a central angle of 45°. The thickness of the prism is 3 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. area of a circle A = πr 2 A = π x 82 45° 3 cm 8 c m area of the given sector A = π x 8 2 x 45 360 volume of the prism 45° 8 cm V = π x 8 2 x 45 x 3 360 V = 24π V ≈ 75. 4 cm 3 [3 s. f. ] © T Madas
 The prism shown has a cross section of a circular sector of radius 8 cm corresponding to a central angle of 45°. The thickness of the prism is 3 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. area of the given sector A = π x 8 2 x 45 360 45° 3 cm 8 c m area of the given sector A = π x 8 2 x 45 360 45° 8 cm © T Madas
The prism shown has a cross section of a circular sector of radius 8 cm corresponding to a central angle of 45°. The thickness of the prism is 3 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. area of the given sector A = π x 8 2 x 45 360 45° 3 cm 8 c m area of the given sector A = π x 8 2 x 45 360 45° 8 cm © T Madas
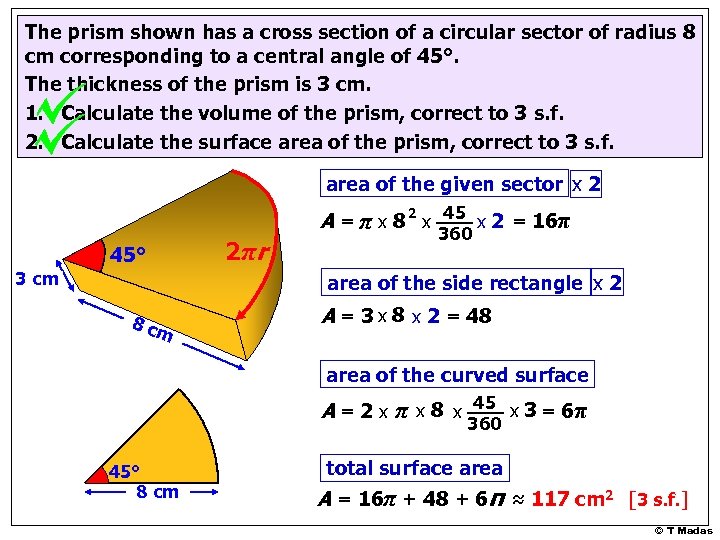 The prism shown has a cross section of a circular sector of radius 8 cm corresponding to a central angle of 45°. The thickness of the prism is 3 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. area of the given sector x 2 A = π x 8 2 x 45 x 2 = 16π 2π r 45° 3 cm 360 area of the side rectangle x 2 8 c m A = 3 x 8 x 2 = 48 area of the curved surface A = 2 x π x 8 x 45 x 3 = 6π 360 45° 8 cm total surface area A = 16π + 48 + 6π ≈ 117 cm 2 [3 s. f. ] © T Madas
The prism shown has a cross section of a circular sector of radius 8 cm corresponding to a central angle of 45°. The thickness of the prism is 3 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. area of the given sector x 2 A = π x 8 2 x 45 x 2 = 16π 2π r 45° 3 cm 360 area of the side rectangle x 2 8 c m A = 3 x 8 x 2 = 48 area of the curved surface A = 2 x π x 8 x 45 x 3 = 6π 360 45° 8 cm total surface area A = 16π + 48 + 6π ≈ 117 cm 2 [3 s. f. ] © T Madas
 © T Madas
© T Madas
 From a cone of height 24 cm and base radius 9 cm, the upper part is removed leaving a frustum of height 8 cm and upper base radius 6 cm. Calculate the volume of this frustum correct to 3 s. f. 24 cm Volume of Original Cone Volume of upper Cone (removed part) 8 cm 6 cm Volume of the frustum 9 cm © T Madas
From a cone of height 24 cm and base radius 9 cm, the upper part is removed leaving a frustum of height 8 cm and upper base radius 6 cm. Calculate the volume of this frustum correct to 3 s. f. 24 cm Volume of Original Cone Volume of upper Cone (removed part) 8 cm 6 cm Volume of the frustum 9 cm © T Madas
 © T Madas
© T Madas
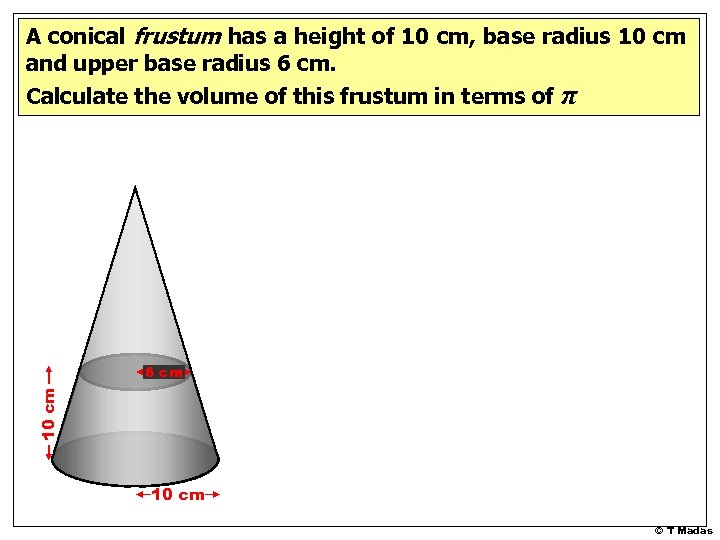 A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π 10 cm 6 cm 10 cm © T Madas
A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π 10 cm 6 cm 10 cm © T Madas
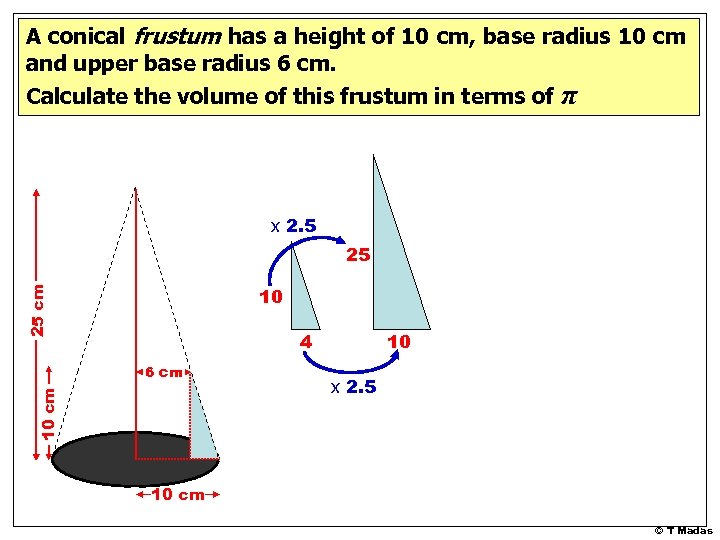 A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π x 2. 5 25 25 cm 10 4 10 cm 6 cm 10 x 2. 5 10 cm © T Madas
A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π x 2. 5 25 25 cm 10 4 10 cm 6 cm 10 x 2. 5 10 cm © T Madas
 A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π 25 cm Volume of “Original” Cone Volume of upper Cone (removed part) 10 cm 6 cm Volume of the frustum 10 cm © T Madas
A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π 25 cm Volume of “Original” Cone Volume of upper Cone (removed part) 10 cm 6 cm Volume of the frustum 10 cm © T Madas
 © T Madas
© T Madas
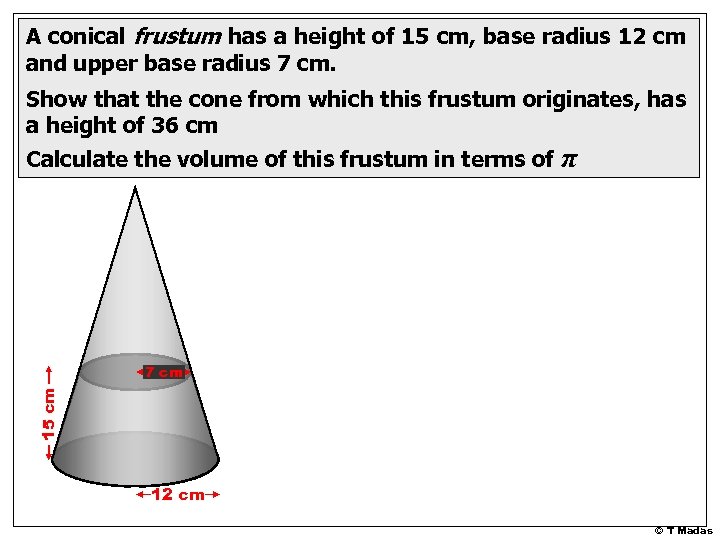 A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 15 cm 7 cm 12 cm © T Madas
A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 15 cm 7 cm 12 cm © T Madas
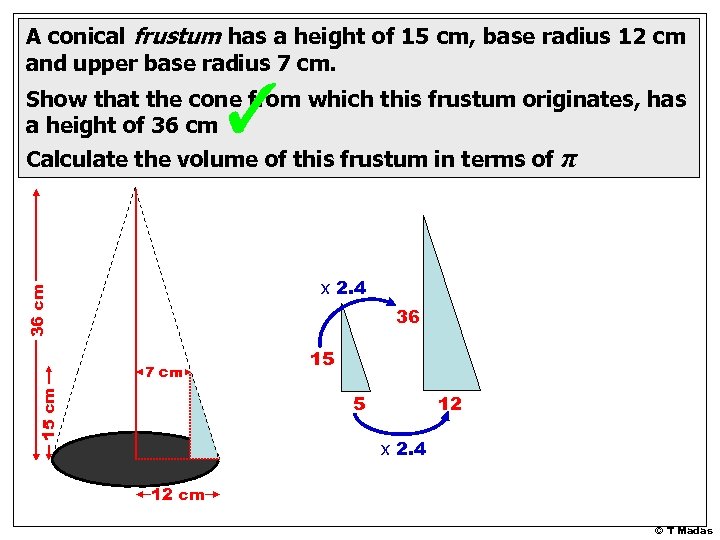 A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 36 cm x 2. 4 36 15 cm 7 cm 15 5 12 x 2. 4 12 cm © T Madas
A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 36 cm x 2. 4 36 15 cm 7 cm 15 5 12 x 2. 4 12 cm © T Madas
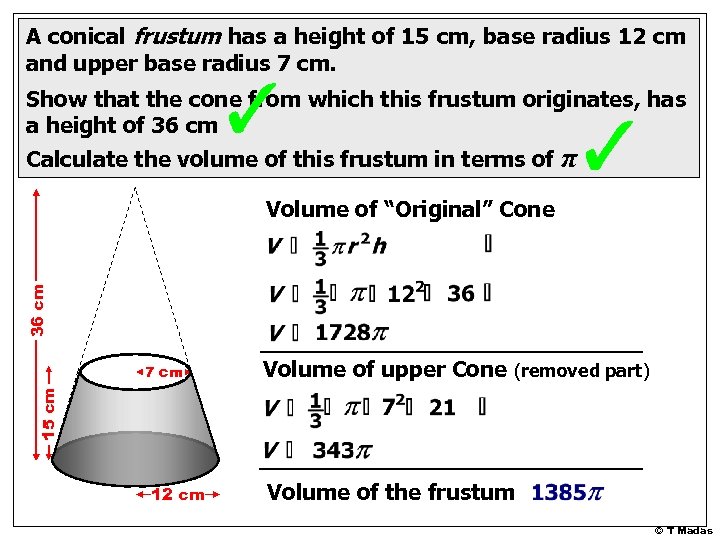 A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 36 cm Volume of “Original” Cone Volume of upper Cone (removed part) 15 cm 7 cm 12 cm Volume of the frustum © T Madas
A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 36 cm Volume of “Original” Cone Volume of upper Cone (removed part) 15 cm 7 cm 12 cm Volume of the frustum © T Madas
 © T Madas
© T Madas
 A cylinder has a height of 12 cm and the radius of its base is 4. 4 cm. These measurements are correct to the nearest mm. Calculate: 1. the volume of the cone to the nearest cm 3. 2. the upper and lower bound for this volume to the nearest cm 3. 3. the percentage error if the actual volume is 715 cm 3 and we use the figure we found in part (1) instead. V = π x 4. 4 x 12 V ≈ 730 cm 3 If the measurements are to the nearest mm, then: 4. 35 ≤ r < 4. 45 11. 95 ≤ h < 12. 05 V = π r 2 h V = π x 4. 352 x 11. 95 c c 2 lower bound of the volume V ≈ 710 cm 3 upper bound of the volume V = π r 2 h V = π x 4. 452 x 12. 05 c c V = πr h 2 c c volume of the cylinder V ≈ 750 cm 3 © T Madas
A cylinder has a height of 12 cm and the radius of its base is 4. 4 cm. These measurements are correct to the nearest mm. Calculate: 1. the volume of the cone to the nearest cm 3. 2. the upper and lower bound for this volume to the nearest cm 3. 3. the percentage error if the actual volume is 715 cm 3 and we use the figure we found in part (1) instead. V = π x 4. 4 x 12 V ≈ 730 cm 3 If the measurements are to the nearest mm, then: 4. 35 ≤ r < 4. 45 11. 95 ≤ h < 12. 05 V = π r 2 h V = π x 4. 352 x 11. 95 c c 2 lower bound of the volume V ≈ 710 cm 3 upper bound of the volume V = π r 2 h V = π x 4. 452 x 12. 05 c c V = πr h 2 c c volume of the cylinder V ≈ 750 cm 3 © T Madas
 A cylinder has a height of 12 cm and the radius of its base is 4. 4 cm. These measurements are correct to the nearest mm. Calculate: 1. the volume of the cone to the nearest cm 3. 2. the upper and lower bound for this volume to the nearest cm 3. 3. the percentage error if the actual volume is 715 cm 3 and we use the figure we found in part (1) instead. V = π r 2 h V = π x 4. 42 x 12 c c volume of the cylinder V ≈ 730 cm 3 If the measurements are to the nearest mm, then: If we use the figure of 730 cm 3 instead of 715 cm 3 … … we have an error of 15 cm 3 … … calculated over the actual volume of 715 cm 3 … 15 x 100 ≈ 2. 1% 715 4. 35 ≤ r < 4. 45 11. 95 ≤ h < 12. 05 © T Madas
A cylinder has a height of 12 cm and the radius of its base is 4. 4 cm. These measurements are correct to the nearest mm. Calculate: 1. the volume of the cone to the nearest cm 3. 2. the upper and lower bound for this volume to the nearest cm 3. 3. the percentage error if the actual volume is 715 cm 3 and we use the figure we found in part (1) instead. V = π r 2 h V = π x 4. 42 x 12 c c volume of the cylinder V ≈ 730 cm 3 If the measurements are to the nearest mm, then: If we use the figure of 730 cm 3 instead of 715 cm 3 … … we have an error of 15 cm 3 … … calculated over the actual volume of 715 cm 3 … 15 x 100 ≈ 2. 1% 715 4. 35 ≤ r < 4. 45 11. 95 ≤ h < 12. 05 © T Madas
 © T Madas
© T Madas
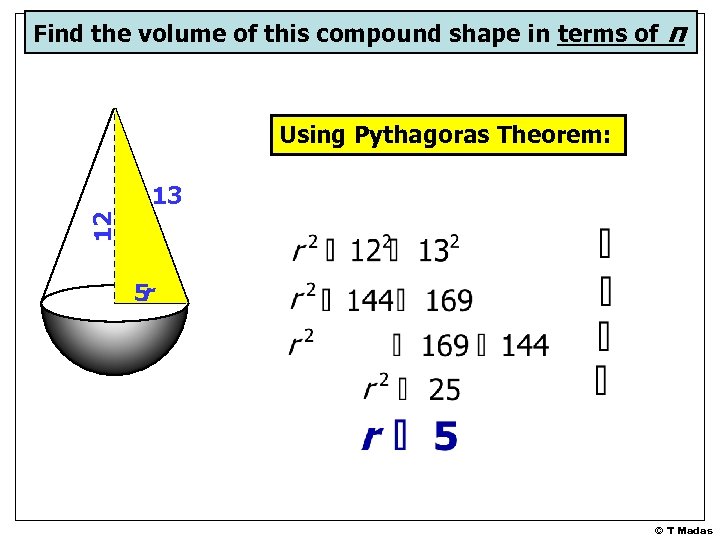 Find the volume of this compound shape in terms of π Using Pythagoras Theorem: 12 13 5 r © T Madas
Find the volume of this compound shape in terms of π Using Pythagoras Theorem: 12 13 5 r © T Madas
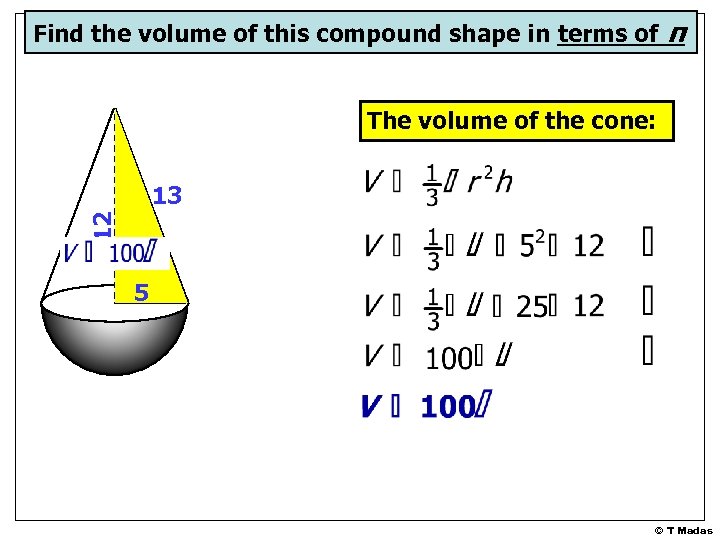 Find the volume of this compound shape in terms of π The volume of the cone: 12 13 5 © T Madas
Find the volume of this compound shape in terms of π The volume of the cone: 12 13 5 © T Madas
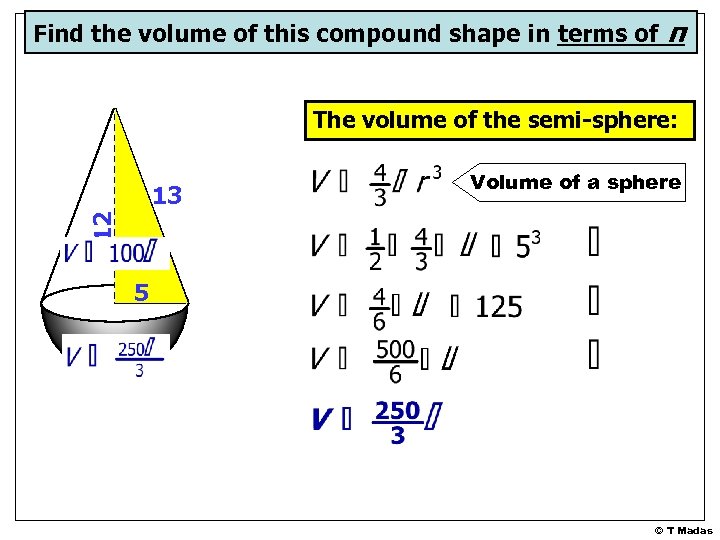 Find the volume of this compound shape in terms of π The volume of the semi-sphere: Volume of a sphere 12 13 5 © T Madas
Find the volume of this compound shape in terms of π The volume of the semi-sphere: Volume of a sphere 12 13 5 © T Madas
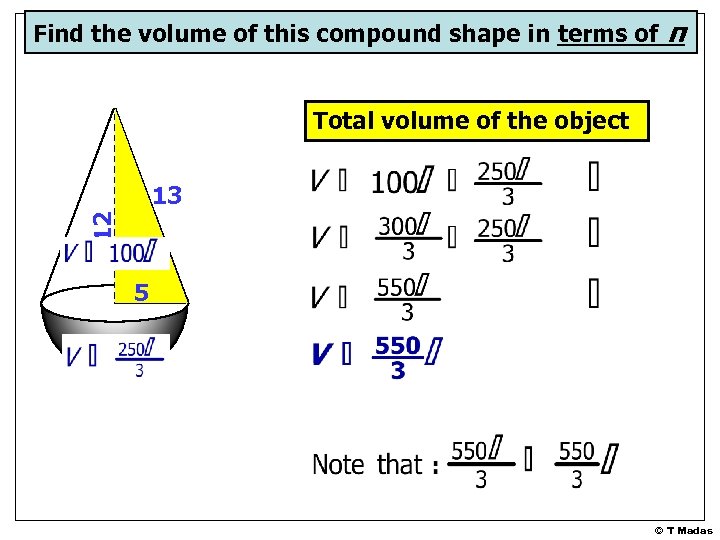 Find the volume of this compound shape in terms of π Total volume of the object 12 13 5 © T Madas
Find the volume of this compound shape in terms of π Total volume of the object 12 13 5 © T Madas
 © T Madas
© T Madas
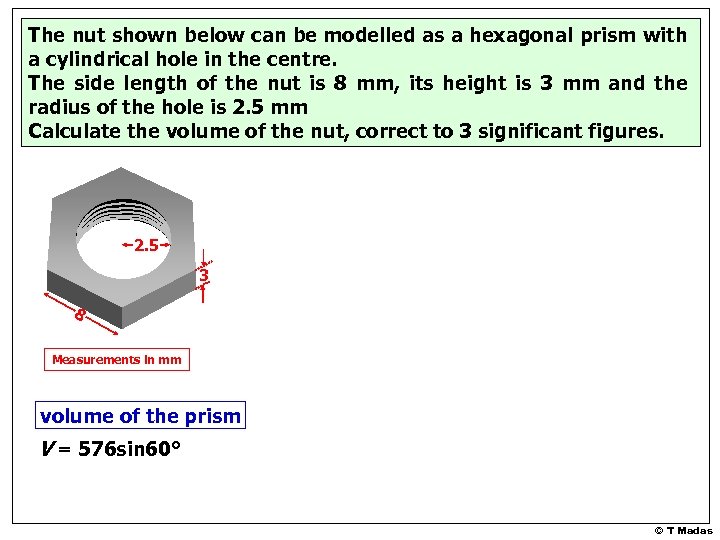
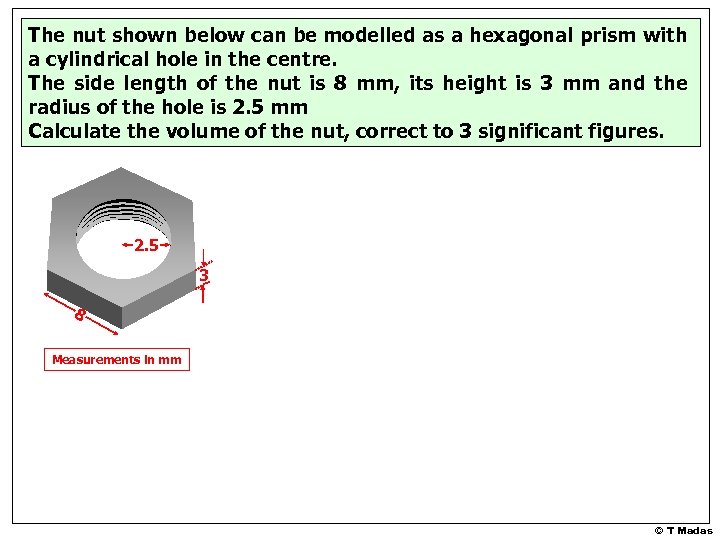 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 2. 5 3 8 Measurements in mm © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 2. 5 3 8 Measurements in mm © T Madas
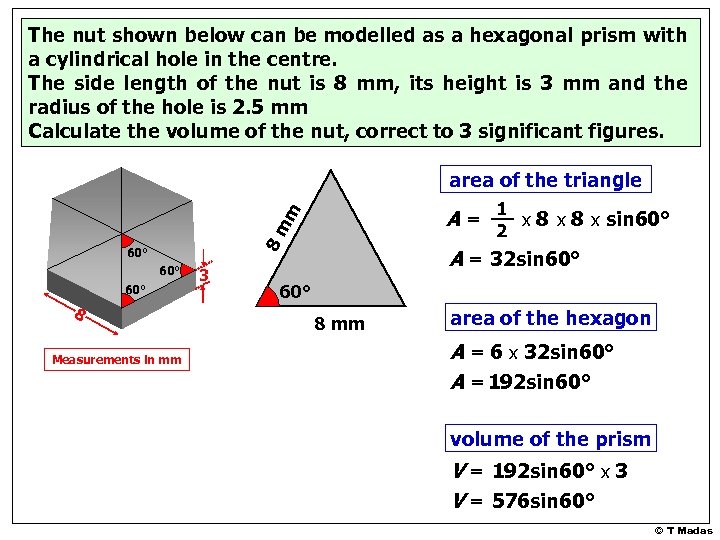 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. area of the triangle m A = 1 x 8 x sin 60° 8 m 2 60° 60° 8 Measurements in mm 3 A = 32 sin 60° 8 mm area of the hexagon A = 6 x 32 sin 60° A = 192 sin 60° volume of the prism V = 192 sin 60° x 3 V = 576 sin 60° © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. area of the triangle m A = 1 x 8 x sin 60° 8 m 2 60° 60° 8 Measurements in mm 3 A = 32 sin 60° 8 mm area of the hexagon A = 6 x 32 sin 60° A = 192 sin 60° volume of the prism V = 192 sin 60° x 3 V = 576 sin 60° © T Madas
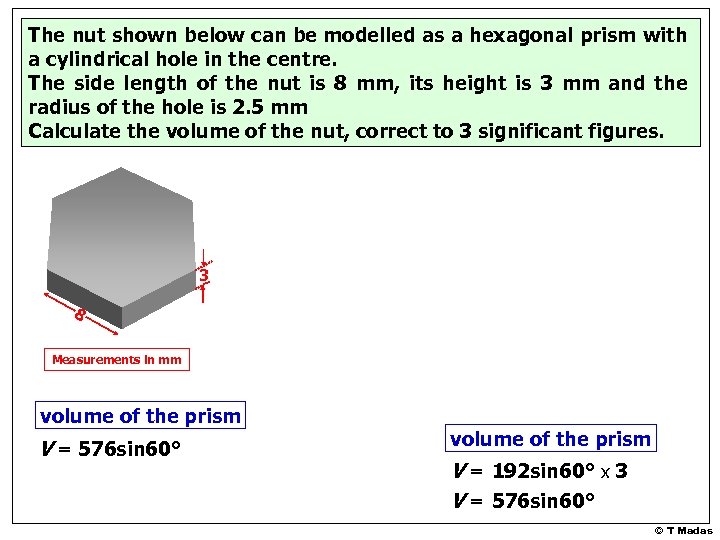 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 3 8 Measurements in mm volume of the prism V = 576 sin 60° volume of the prism V = 192 sin 60° x 3 V = 576 sin 60° © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 3 8 Measurements in mm volume of the prism V = 576 sin 60° volume of the prism V = 192 sin 60° x 3 V = 576 sin 60° © T Madas
 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 2. 5 3 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 2. 5 3 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas
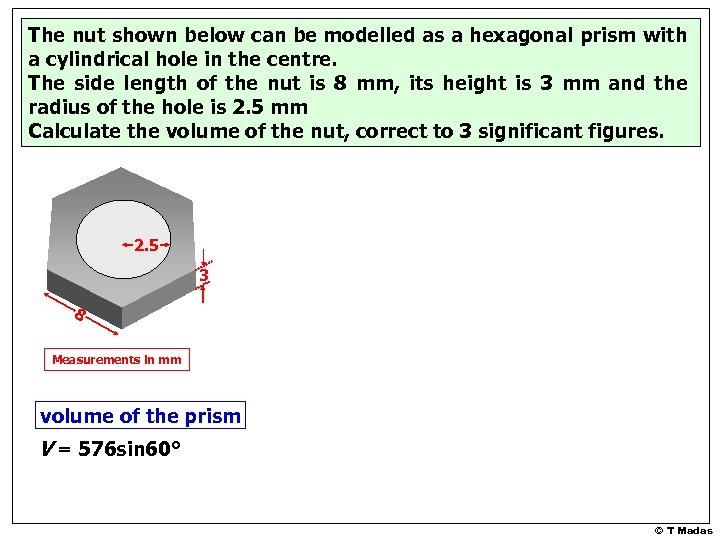 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 2. 5 3 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 2. 5 3 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas
 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 3 2 V = π x 2. 5 x 3 V = 18. 75 π Measurements in mm volume of the prism V = 576 sin 60° © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 3 2 V = π x 2. 5 x 3 V = 18. 75 π Measurements in mm volume of the prism V = 576 sin 60° © T Madas
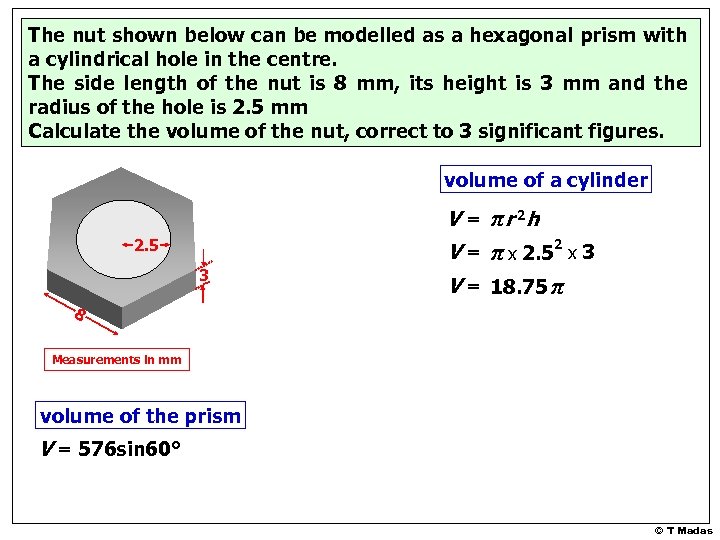 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 2 V = π x 2. 5 x 3 3 V = 18. 75 π 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 2 V = π x 2. 5 x 3 3 V = 18. 75 π 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas
 The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 2 V = π x 2. 5 x 3 3 V = 18. 75 π 8 Measurements in mm volume of the nut volume of the prism 576 sin 60° – 18. 75 π V = 576 sin 60° 440 mm 3 [ 3 s. f. ] © T Madas
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 2 V = π x 2. 5 x 3 3 V = 18. 75 π 8 Measurements in mm volume of the nut volume of the prism 576 sin 60° – 18. 75 π V = 576 sin 60° 440 mm 3 [ 3 s. f. ] © T Madas
 © T Madas
© T Madas
 A metal ball bearing can be modelled as a sphere of radius 2. 5 cm. The ball bearing is to be melted and remoulded into the shape of a cone with a height of 4. 8 cm. Calculate the radius of the base of the cone, in cm correct to 2 significant figures. volume of the sphere V= 4 3 πr 3 = 4 x 3 π x 2. 53 ≈ 65. 4498 cm 3 volume of the cone 1 3 πr 2 h = 1 x 3 π x r 2 x 4. 8 ≈ 5. 0265 r 2 cm 3 5. 0265 r 2 = 65. 4498 r 2 = 13. 0209 r = 3. 6 cm c c c V= [2 s. f. ] © T Madas
A metal ball bearing can be modelled as a sphere of radius 2. 5 cm. The ball bearing is to be melted and remoulded into the shape of a cone with a height of 4. 8 cm. Calculate the radius of the base of the cone, in cm correct to 2 significant figures. volume of the sphere V= 4 3 πr 3 = 4 x 3 π x 2. 53 ≈ 65. 4498 cm 3 volume of the cone 1 3 πr 2 h = 1 x 3 π x r 2 x 4. 8 ≈ 5. 0265 r 2 cm 3 5. 0265 r 2 = 65. 4498 r 2 = 13. 0209 r = 3. 6 cm c c c V= [2 s. f. ] © T Madas
 © T Madas
© T Madas
 One of the two sections of a sand timer can be modelled as a semi sphere connected to a cylinder which is in turn connected to a cone. All three solids share the same axis of symmetry. The radius of these solids is 3 cm and the heights of the cylinder and the cone are 9 cm and 3 cm respectively. Calculate the volume of the sand timer in terms of π. 3 9 4 x 3 3 π x 33 x 18π π x 32 x 9 3 81π 3 Measurements in cm 1 x 3 π x 32 x 3 9π 1 2 volume of a sphere V= 4 3 πr 3 volume of a cylinder V = π r 2 h volume of a cone V= 1 3 πr 2 h © T Madas
One of the two sections of a sand timer can be modelled as a semi sphere connected to a cylinder which is in turn connected to a cone. All three solids share the same axis of symmetry. The radius of these solids is 3 cm and the heights of the cylinder and the cone are 9 cm and 3 cm respectively. Calculate the volume of the sand timer in terms of π. 3 9 4 x 3 3 π x 33 x 18π π x 32 x 9 3 81π 3 Measurements in cm 1 x 3 π x 32 x 3 9π 1 2 volume of a sphere V= 4 3 πr 3 volume of a cylinder V = π r 2 h volume of a cone V= 1 3 πr 2 h © T Madas
 One of the two sections of a sand timer can be modelled as a semi sphere connected to a cylinder which is in turn connected to a cone. All three solids share the same axis of symmetry. The radius of these solids is 3 cm and the heights of the cylinder and the cone are 9 cm and 3 cm respectively. Calculate the volume of the sand timer in terms of π. 216π 3 108π 9 4 x 3 3 π x 33 x ≈ 679 cm 3 1 2 18π π x 32 x 9 3 81π 108π Measurements in cm 3 1 x 3 π x 32 x 3 9π © T Madas
One of the two sections of a sand timer can be modelled as a semi sphere connected to a cylinder which is in turn connected to a cone. All three solids share the same axis of symmetry. The radius of these solids is 3 cm and the heights of the cylinder and the cone are 9 cm and 3 cm respectively. Calculate the volume of the sand timer in terms of π. 216π 3 108π 9 4 x 3 3 π x 33 x ≈ 679 cm 3 1 2 18π π x 32 x 9 3 81π 108π Measurements in cm 3 1 x 3 π x 32 x 3 9π © T Madas
 © T Madas
© T Madas
 A cylindrical bucket of radius 9 cm contains some water. A metal sphere is gently lowered into the water, raising its level by 6 cm which completely covers the sphere. Calculate the radius of the sphere to the nearest cm. © T Madas
A cylindrical bucket of radius 9 cm contains some water. A metal sphere is gently lowered into the water, raising its level by 6 cm which completely covers the sphere. Calculate the radius of the sphere to the nearest cm. © T Madas
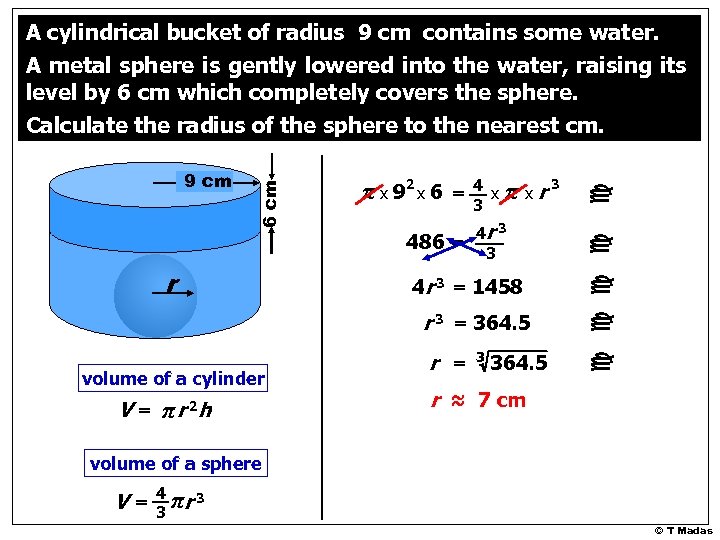 486 = r 4 x 3 π x r 3 4 r 3 = 1458 r 3 = 364. 5 volume of a cylinder V = π r 2 h r = 3 364. 5 c π x 92 x 6 = c c 9 cm 6 cm A cylindrical bucket of radius 9 cm contains some water. A metal sphere is gently lowered into the water, raising its level by 6 cm which completely covers the sphere. Calculate the radius of the sphere to the nearest cm. r ≈ 7 cm volume of a sphere V= 4 3 πr 3 © T Madas
486 = r 4 x 3 π x r 3 4 r 3 = 1458 r 3 = 364. 5 volume of a cylinder V = π r 2 h r = 3 364. 5 c π x 92 x 6 = c c 9 cm 6 cm A cylindrical bucket of radius 9 cm contains some water. A metal sphere is gently lowered into the water, raising its level by 6 cm which completely covers the sphere. Calculate the radius of the sphere to the nearest cm. r ≈ 7 cm volume of a sphere V= 4 3 πr 3 © T Madas
 © T Madas
© T Madas
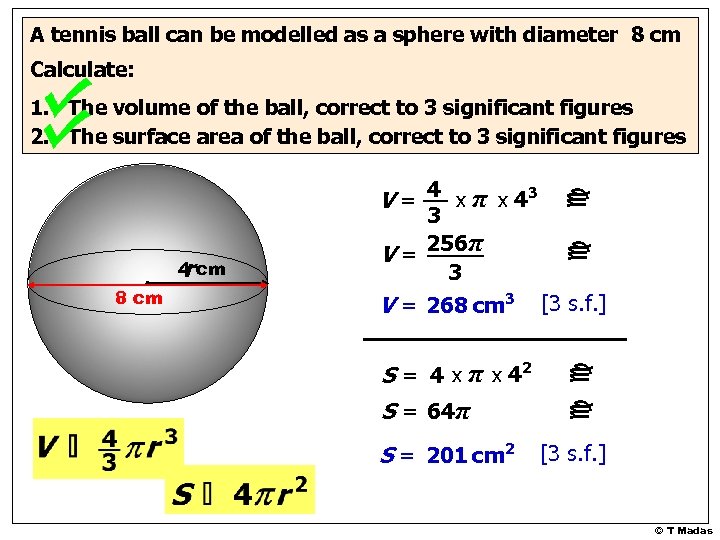 A tennis ball can be modelled as a sphere with diameter 8 cm Calculate: 8 cm S = 4 x π x 42 S = 64π S = 201 cm 2 c 4 cm r 3 V = 256π 3 V = 268 cm 3 [3 s. f. ] c c V = 4 x π x 43 c 1. The volume of the ball, correct to 3 significant figures 2. The surface area of the ball, correct to 3 significant figures [3 s. f. ] © T Madas
A tennis ball can be modelled as a sphere with diameter 8 cm Calculate: 8 cm S = 4 x π x 42 S = 64π S = 201 cm 2 c 4 cm r 3 V = 256π 3 V = 268 cm 3 [3 s. f. ] c c V = 4 x π x 43 c 1. The volume of the ball, correct to 3 significant figures 2. The surface area of the ball, correct to 3 significant figures [3 s. f. ] © T Madas
 © T Madas
© T Madas
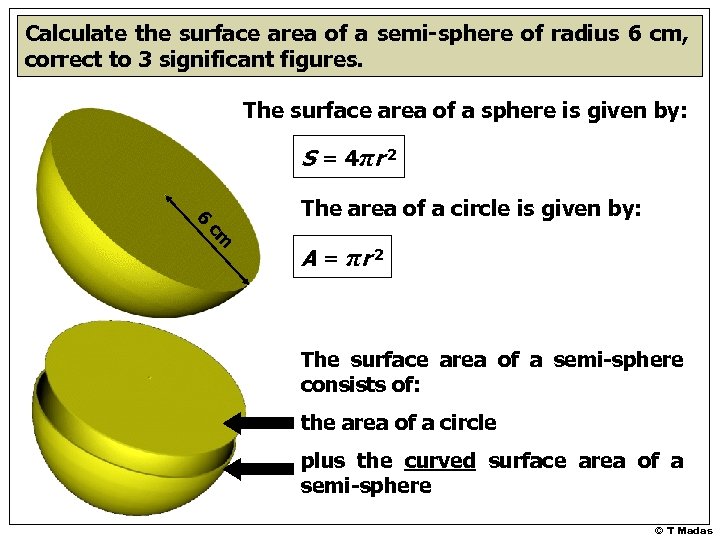 Calculate the surface area of a semi-sphere of radius 6 cm, correct to 3 significant figures. The surface area of a sphere is given by: S = 4π r 2 6 The area of a circle is given by: cm A = πr 2 The surface area of a semi-sphere consists of: the area of a circle plus the curved surface area of a semi-sphere © T Madas
Calculate the surface area of a semi-sphere of radius 6 cm, correct to 3 significant figures. The surface area of a sphere is given by: S = 4π r 2 6 The area of a circle is given by: cm A = πr 2 The surface area of a semi-sphere consists of: the area of a circle plus the curved surface area of a semi-sphere © T Madas
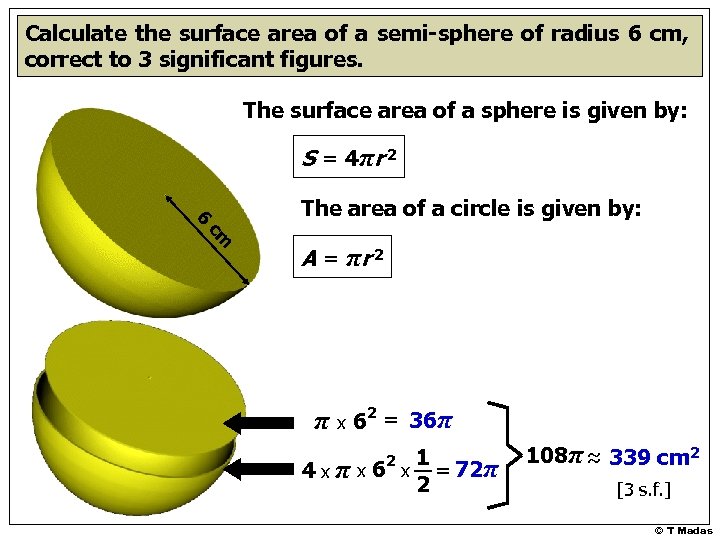 Calculate the surface area of a semi-sphere of radius 6 cm, correct to 3 significant figures. The surface area of a sphere is given by: S = 4π r 2 6 The area of a circle is given by: cm A = πr 2 π x 62 = 36π 1 4 x π x 6 x = 72π 2 2 108π ≈ 339 cm 2 [3 s. f. ] © T Madas
Calculate the surface area of a semi-sphere of radius 6 cm, correct to 3 significant figures. The surface area of a sphere is given by: S = 4π r 2 6 The area of a circle is given by: cm A = πr 2 π x 62 = 36π 1 4 x π x 6 x = 72π 2 2 108π ≈ 339 cm 2 [3 s. f. ] © T Madas
 © T Madas
© T Madas
 The figure below shows the cross section of a cylinder of base radius a with 3 spheres fitting “snugly” inside it. 1. Calculate the volume of the cylinder in terms of a. 2. Write down the volume of the three spheres. 3. Hence calculate what fraction of the cylinder is empty volume of a cylinder V = πr h Vc = πa 2 x 6 a 2 6 a Vc = 6 πa 3 volume of a sphere V= πr 3 V 3 s = a 4 3 πa 3 x 3 V 3 s = 4 πa 3 Vc = 6π a 3 V 3 s = 4πa 3 Empty = 2πa 3 Empty Vc 2π a 3 1 = = 3 3 6π a What fraction would it be if 5 spheres fitted snugly inside a cylinder with the appropriate dimensions? © T Madas
The figure below shows the cross section of a cylinder of base radius a with 3 spheres fitting “snugly” inside it. 1. Calculate the volume of the cylinder in terms of a. 2. Write down the volume of the three spheres. 3. Hence calculate what fraction of the cylinder is empty volume of a cylinder V = πr h Vc = πa 2 x 6 a 2 6 a Vc = 6 πa 3 volume of a sphere V= πr 3 V 3 s = a 4 3 πa 3 x 3 V 3 s = 4 πa 3 Vc = 6π a 3 V 3 s = 4πa 3 Empty = 2πa 3 Empty Vc 2π a 3 1 = = 3 3 6π a What fraction would it be if 5 spheres fitted snugly inside a cylinder with the appropriate dimensions? © T Madas
 © T Madas
© T Madas
 A sphere with a radius of α cm has the same volume as a cone with a base radius of α cm. Find the height of the cone, in terms of α. volume of the sphere πα 3 V= 4 3 πα 3 = 4 3 3 x α 3= 4 3 α= 1 3 π α 2 h 1 3 α 2 h c c 4 3 1 3 h x 3 c V= volume of the cone π α 2 h 4α = h h = 4α , i. e. the height of the cone is 4 times the base radius © T Madas
A sphere with a radius of α cm has the same volume as a cone with a base radius of α cm. Find the height of the cone, in terms of α. volume of the sphere πα 3 V= 4 3 πα 3 = 4 3 3 x α 3= 4 3 α= 1 3 π α 2 h 1 3 α 2 h c c 4 3 1 3 h x 3 c V= volume of the cone π α 2 h 4α = h h = 4α , i. e. the height of the cone is 4 times the base radius © T Madas
 © T Madas
© T Madas
 The Earth can be modelled as a sphere of radius 6 400 000 m and it is estimated that 360 000 000 m 2 are covered by sea. 1. Write 360 000 000 in standard form. 2. Calculate the surface area of the Earth in m 2, giving your answer in standard form correct to 3 significant figures. 3. Calculate what percentage of the Earth’s surface is covered by sea, giving your answer to the nearest percentage. 360 000 000 = 3. 6 x 1014 The surface area of a sphere is given by: S = 4π r 2 S = 4 x π x 64000002 ≈ 5. 15 x 1014 m 2 3. 6 x 1014 x 100 ≈ 70% 5. 15 x 1014 © T Madas
The Earth can be modelled as a sphere of radius 6 400 000 m and it is estimated that 360 000 000 m 2 are covered by sea. 1. Write 360 000 000 in standard form. 2. Calculate the surface area of the Earth in m 2, giving your answer in standard form correct to 3 significant figures. 3. Calculate what percentage of the Earth’s surface is covered by sea, giving your answer to the nearest percentage. 360 000 000 = 3. 6 x 1014 The surface area of a sphere is given by: S = 4π r 2 S = 4 x π x 64000002 ≈ 5. 15 x 1014 m 2 3. 6 x 1014 x 100 ≈ 70% 5. 15 x 1014 © T Madas
 © T Madas
© T Madas
 x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 27π x 2π x • • • let the cylinder have a radius x cm then the height will be (x + 7. 5) cm the curved face is a rectangle… of base 2πx … height (x + 7. 5) … and area 27π © T Madas
x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 27π x 2π x • • • let the cylinder have a radius x cm then the height will be (x + 7. 5) cm the curved face is a rectangle… of base 2πx … height (x + 7. 5) … and area 27π © T Madas
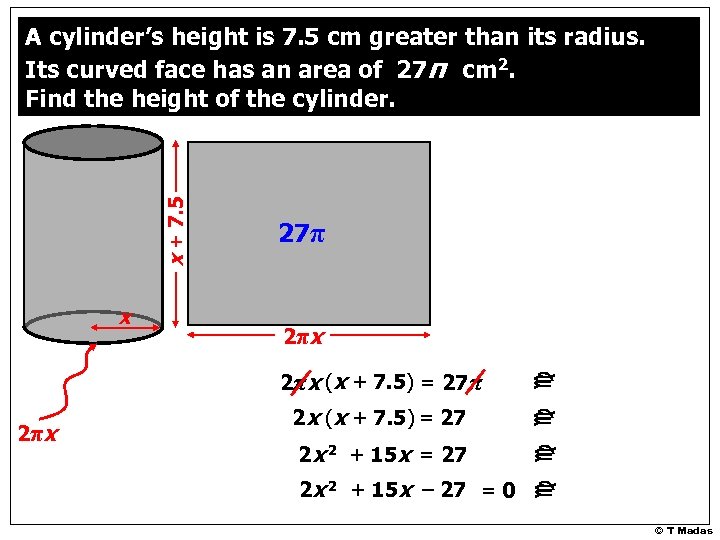 x 27π 2π x 2πx (x + 7. 5) = 27π 2π x 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 c c x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. © T Madas
x 27π 2π x 2πx (x + 7. 5) = 27π 2π x 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 c c x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. © T Madas
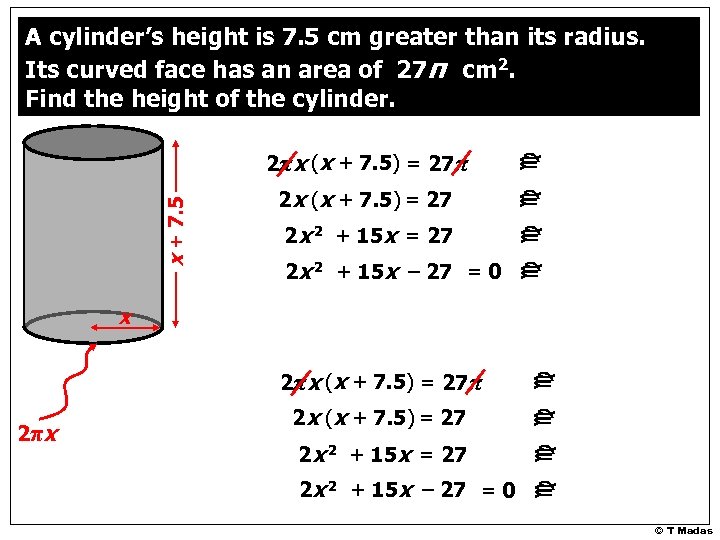 x + 7. 5 2πx (x + 7. 5) = 27π 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 c c A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 2πx (x + 7. 5) = 27π 2π x 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 c c x © T Madas
x + 7. 5 2πx (x + 7. 5) = 27π 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 c c A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 2πx (x + 7. 5) = 27π 2π x 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 c c x © T Madas
 x + 7. 5 2πx (x + 7. 5) = 27π x 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 2 x – 3 x + 9 = 0 c c c A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 1. 5 cm x= 2π x -9 Therefore the height of the cylinder is 9 cm © T Madas
x + 7. 5 2πx (x + 7. 5) = 27π x 2 x (x + 7. 5) = 27 2 x 2 + 15 x – 27 = 0 2 x – 3 x + 9 = 0 c c c A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 1. 5 cm x= 2π x -9 Therefore the height of the cylinder is 9 cm © T Madas
 © T Madas
© T Madas


