4effb5c4d7da44cd8c673060efa2fa70.ppt
- Количество слайдов: 62
 © T Madas
© T Madas
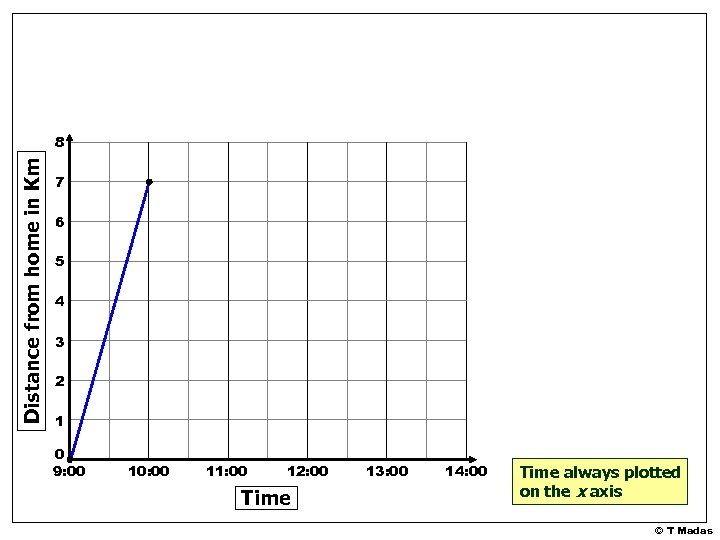
 Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
 Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
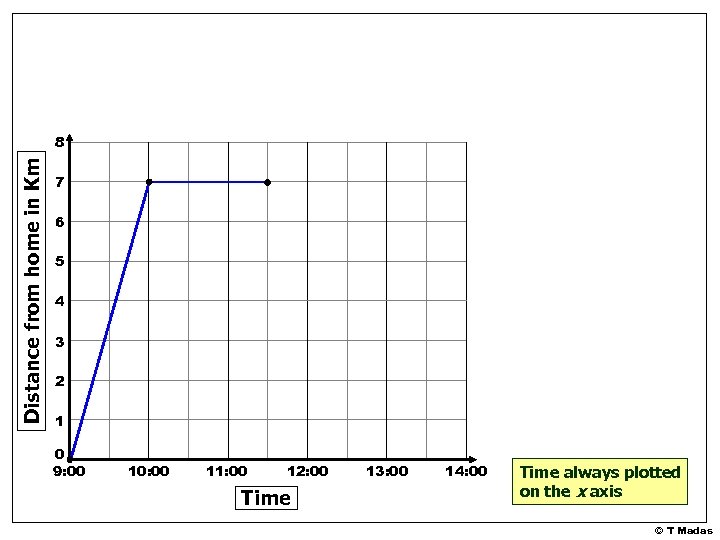
 Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
 Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
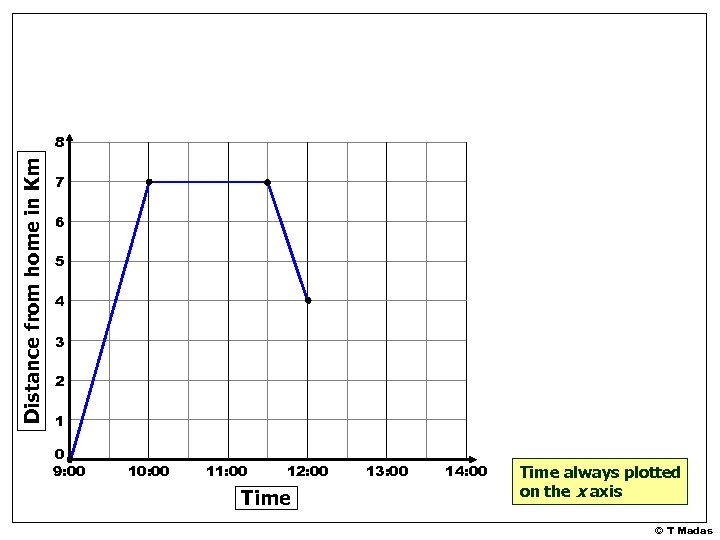
 Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
 Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
 Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
 Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
 Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for an half hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for an half hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
 Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
 Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Draw a distance-time graph for this information • Marc started from his house at 9 a. m. cycling at constant speed to Andy’s house, 7 km away. • He arrived there one hour later. • Marc stayed at Andy’s for 1½ hours. • He started cycling back home. • Half hour into his return journey he stopped at Elli’s house that lives 4 km from his house. • He stayed at Elli’s for half an hour. • He continued cycling home at constant speed arriving back at 2 p. m. © T Madas
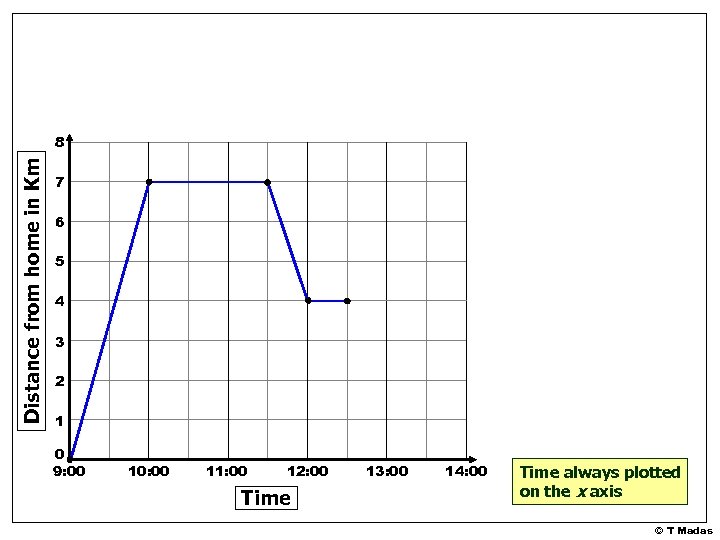
 What do the “flat” parts of the graph represent? Flat = not travelling/a stop Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
What do the “flat” parts of the graph represent? Flat = not travelling/a stop Distance from home in Km 8 7 6 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
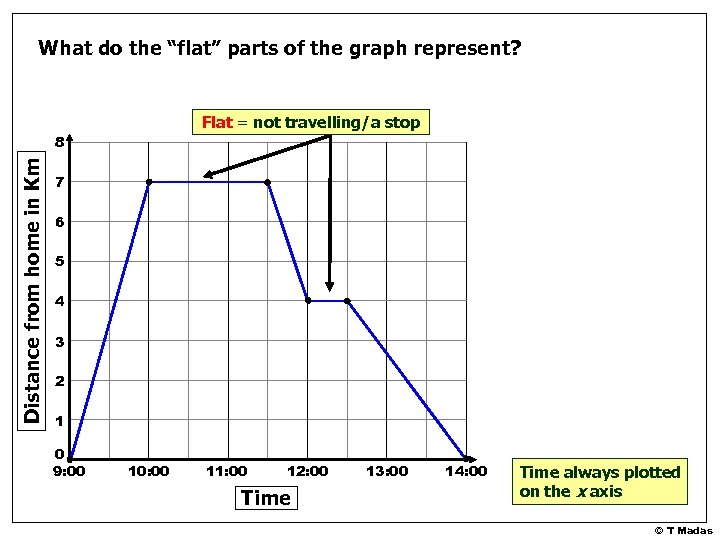
 What do the “uphill” parts of the graph represent? Flat = not travelling/a stop Distance from home in Km 8 7 6 5 4 3 2 Uphill = travelling away 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
What do the “uphill” parts of the graph represent? Flat = not travelling/a stop Distance from home in Km 8 7 6 5 4 3 2 Uphill = travelling away 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
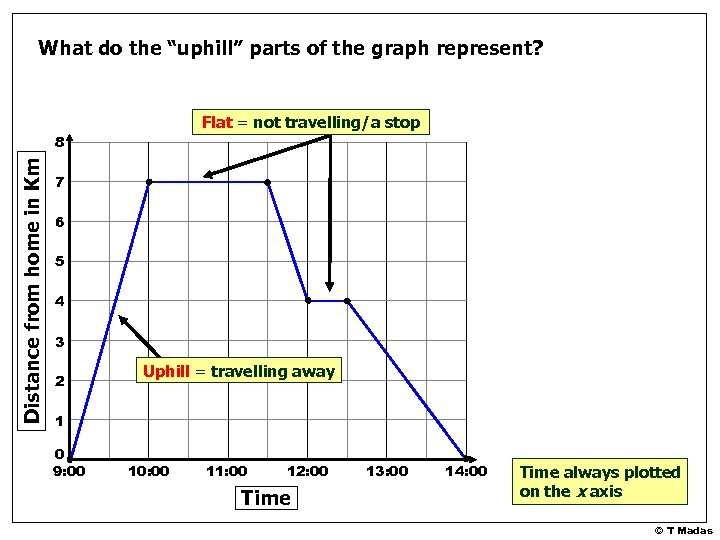
 What do the “down hill” parts of the graph represent? Flat = not travelling/a stop Distance from home in Km 8 7 6 Downhill = travelling back 5 4 3 2 Uphill = travelling away 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
What do the “down hill” parts of the graph represent? Flat = not travelling/a stop Distance from home in Km 8 7 6 Downhill = travelling back 5 4 3 2 Uphill = travelling away 1 0 9: 00 10: 00 11: 00 12: 00 Time 13: 00 14: 00 Time always plotted on the x axis © T Madas
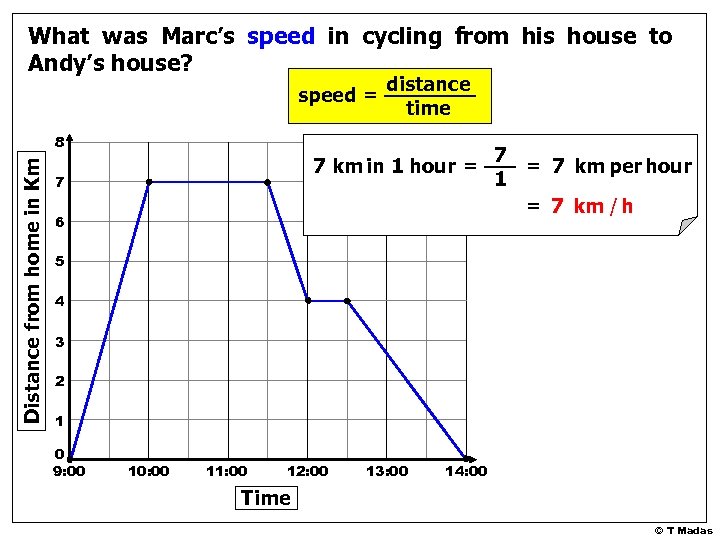 What was Marc’s speed in cycling from his house to Andy’s house? speed = distance time Distance from home in Km 8 7 km in 1 hour = 7 6 7 = 7 km per hour 1 = 7 km / h 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
What was Marc’s speed in cycling from his house to Andy’s house? speed = distance time Distance from home in Km 8 7 km in 1 hour = 7 6 7 = 7 km per hour 1 = 7 km / h 5 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
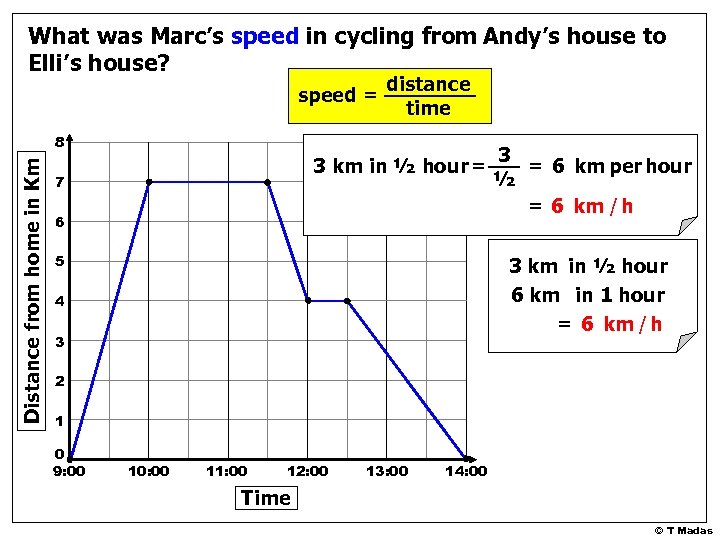 What was Marc’s speed in cycling from Andy’s house to Elli’s house? speed = distance time Distance from home in Km 8 3 km in ½ hour = 7 6 5 3 = 6 km per hour ½ = 6 km / h 3 km in ½ hour 6 km in 1 hour = 6 km / h 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
What was Marc’s speed in cycling from Andy’s house to Elli’s house? speed = distance time Distance from home in Km 8 3 km in ½ hour = 7 6 5 3 = 6 km per hour ½ = 6 km / h 3 km in ½ hour 6 km in 1 hour = 6 km / h 4 3 2 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
 What was Marc’s speed in cycling from Ellis’s house back home? speed = distance time Distance from home in Km 8 4 km in 1½ hour = 7 6 5 4 ≈ 2. 67 km per hour 1. 5 ≈ 2. 67 km / h 4 km in 1½ hour 8 km in 3 hours 2 8 8 ÷ 3 = = 2 km / h 3 3 4 3 ≈ 2. 67 km / h 2 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
What was Marc’s speed in cycling from Ellis’s house back home? speed = distance time Distance from home in Km 8 4 km in 1½ hour = 7 6 5 4 ≈ 2. 67 km per hour 1. 5 ≈ 2. 67 km / h 4 km in 1½ hour 8 km in 3 hours 2 8 8 ÷ 3 = = 2 km / h 3 3 4 3 ≈ 2. 67 km / h 2 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
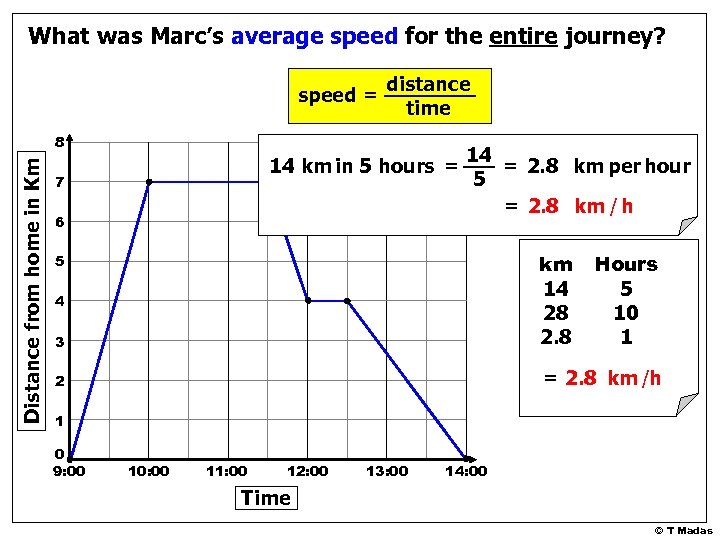 What was Marc’s average speed for the entire journey? speed = distance time Distance from home in Km 8 14 km in 5 hours = 7 6 14 = 2. 8 km per hour 5 = 2. 8 km / h 3 km 14 28 2. 8 2 = 2. 8 km /h 5 4 Hours 5 10 1 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
What was Marc’s average speed for the entire journey? speed = distance time Distance from home in Km 8 14 km in 5 hours = 7 6 14 = 2. 8 km per hour 5 = 2. 8 km / h 3 km 14 28 2. 8 2 = 2. 8 km /h 5 4 Hours 5 10 1 1 0 9: 00 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
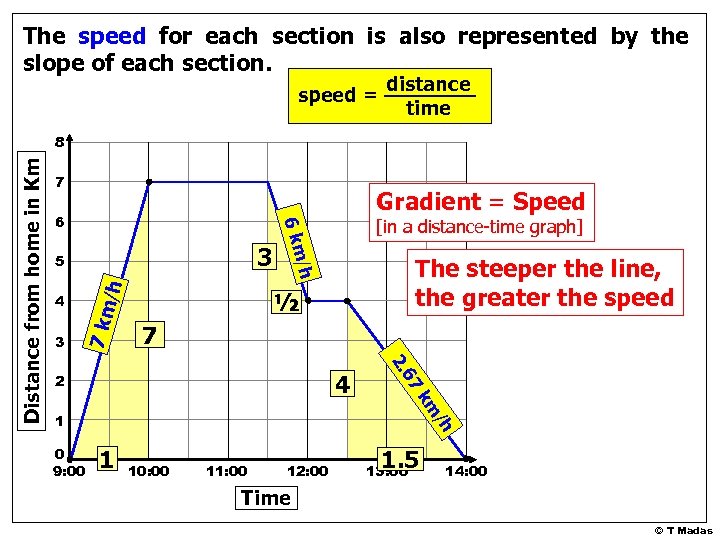 The speed for each section is also represented by the slope of each section. speed = distance time 7 6 3 /h 7 km 4 [in a distance-time graph] The steeper the line, the greater the speed /h 3 5 Gradient = Speed m -6 k ½ 7 7 km 4 2 . 6 -2 1 0 9: 00 /h Distance from home in Km 8 1 10: 00 11: 00 12: 00 1. 5 13: 00 14: 00 Time © T Madas
The speed for each section is also represented by the slope of each section. speed = distance time 7 6 3 /h 7 km 4 [in a distance-time graph] The steeper the line, the greater the speed /h 3 5 Gradient = Speed m -6 k ½ 7 7 km 4 2 . 6 -2 1 0 9: 00 /h Distance from home in Km 8 1 10: 00 11: 00 12: 00 1. 5 13: 00 14: 00 Time © T Madas
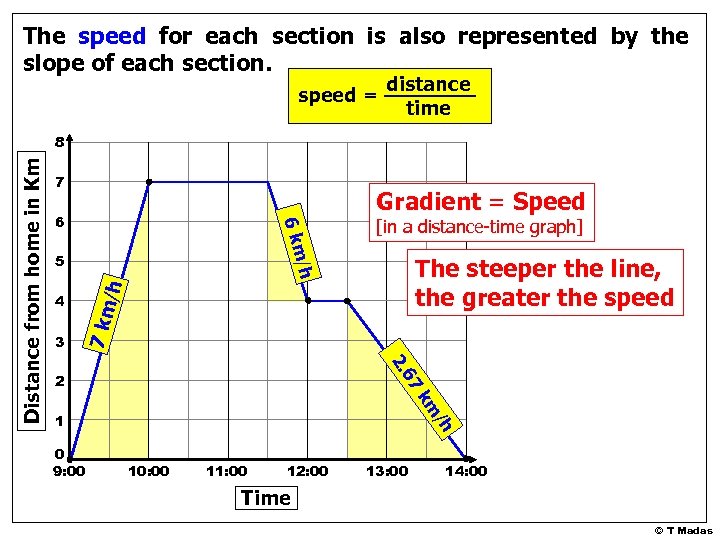 The speed for each section is also represented by the slope of each section. speed = distance time 7 6 m -6 k 5 3 [in a distance-time graph] The steeper the line, the greater the speed /h 7 km 4 Gradient = Speed /h . 6 -2 2 7 km 1 0 9: 00 /h Distance from home in Km 8 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
The speed for each section is also represented by the slope of each section. speed = distance time 7 6 m -6 k 5 3 [in a distance-time graph] The steeper the line, the greater the speed /h 7 km 4 Gradient = Speed /h . 6 -2 2 7 km 1 0 9: 00 /h Distance from home in Km 8 10: 00 11: 00 12: 00 13: 00 14: 00 Time © T Madas
 Distance-Time Graphs Summary Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Time is always plotted on the x axis the “flat” parts of the graph indicate stops (no motion) the “uphill” parts indicate travelling away from the starting point the “downhill” parts indicate travelling back to the starting point To find the speed we use: speed = distance time The speed in a distance-time graph is given by the slope (also called gradient) of a line © T Madas
Distance-Time Graphs Summary Graphs which show the distance of an object from a starting point changes with time, are called distance-time graphs or simply travel-graphs Time is always plotted on the x axis the “flat” parts of the graph indicate stops (no motion) the “uphill” parts indicate travelling away from the starting point the “downhill” parts indicate travelling back to the starting point To find the speed we use: speed = distance time The speed in a distance-time graph is given by the slope (also called gradient) of a line © T Madas
 © T Madas
© T Madas
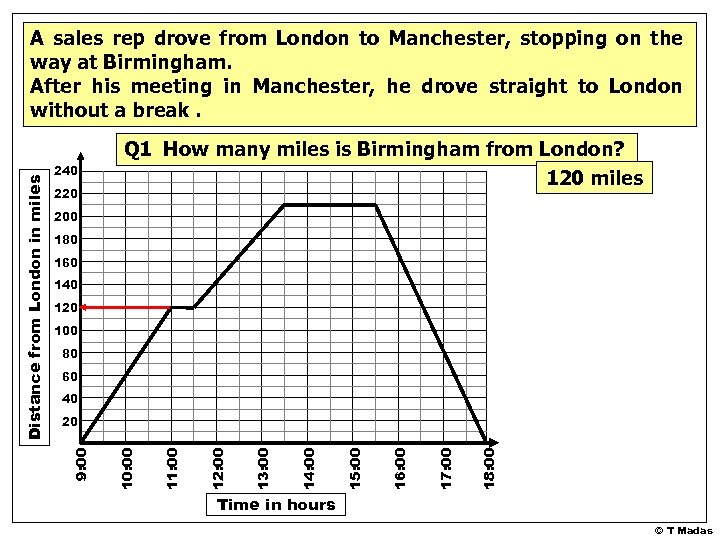 240 220 Q 1 How many miles is Birmingham from London? 120 miles 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
240 220 Q 1 How many miles is Birmingham from London? 120 miles 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
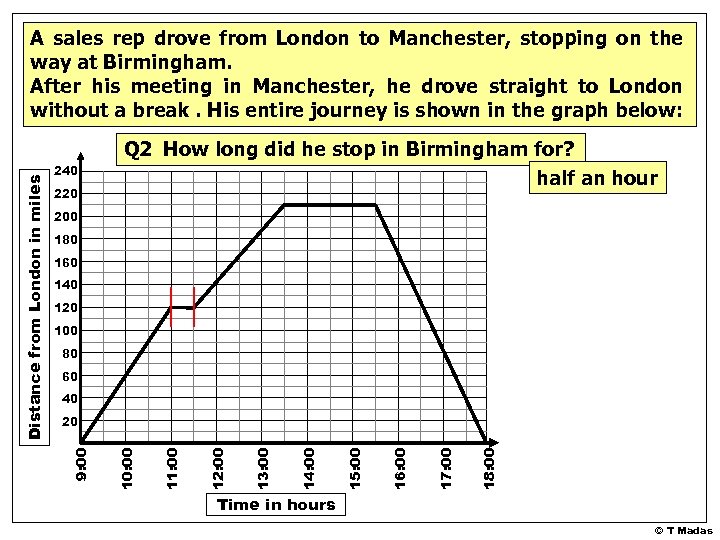 240 220 Q 2 How long did he stop in Birmingham for? half an hour 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
240 220 Q 2 How long did he stop in Birmingham for? half an hour 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
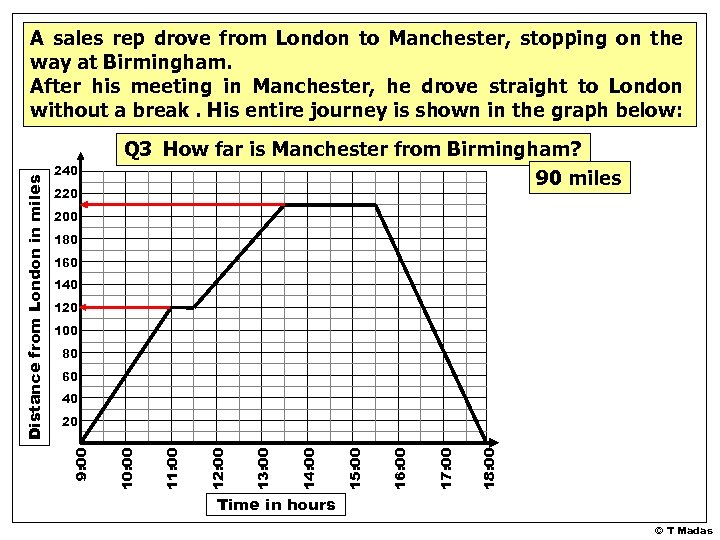 240 220 Q 3 How far is Manchester from Birmingham? 90 miles 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
240 220 Q 3 How far is Manchester from Birmingham? 90 miles 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
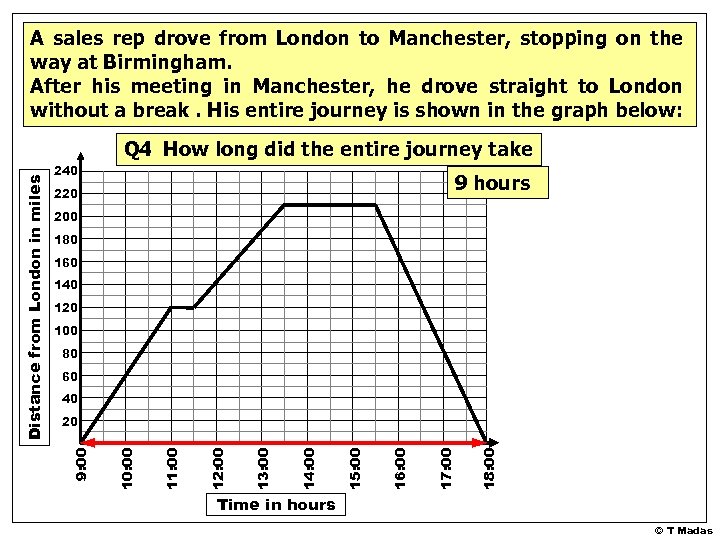 A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: 240 9 hours 220 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles Q 4 How long did the entire journey take Time in hours © T Madas
A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: 240 9 hours 220 200 180 160 140 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles Q 4 How long did the entire journey take Time in hours © T Madas
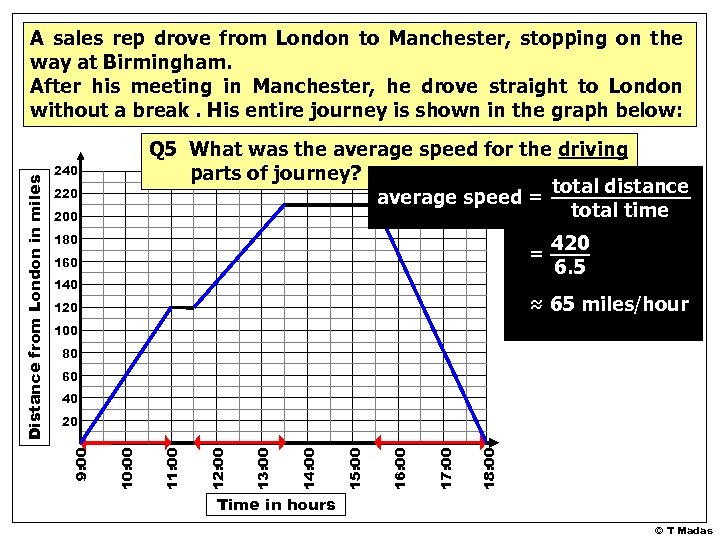 Q 5 What was the average speed for the driving parts of journey? total distance average speed = total time 240 220 200 180 = 160 140 420 6. 5 ≈ 65 miles/hour 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
Q 5 What was the average speed for the driving parts of journey? total distance average speed = total time 240 220 200 180 = 160 140 420 6. 5 ≈ 65 miles/hour 120 100 80 60 40 18: 00 17: 00 16: 00 15: 00 14: 00 13: 00 12: 00 11: 00 10: 00 20 9: 00 Distance from London in miles A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: Time in hours © T Madas
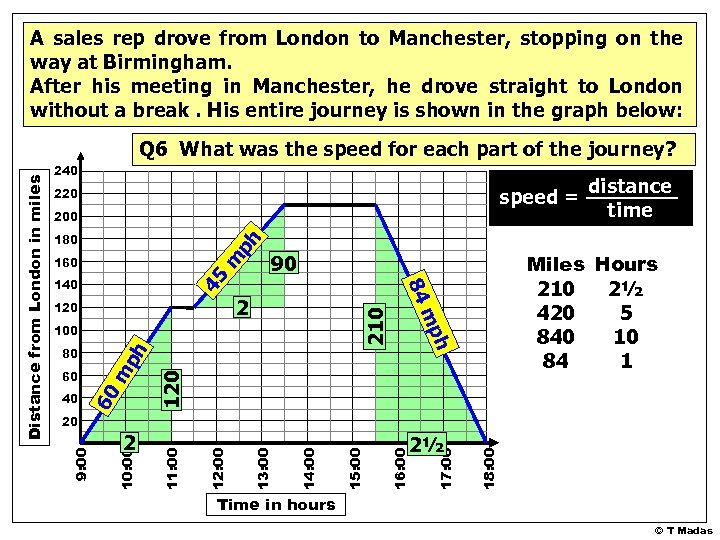 A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: 240 speed = 220 200 ph 180 140 40 m ph 60 60 h 80 120 100 mp 210 2 120 distance time Miles Hours 210 2½ 420 5 840 10 84 1 90 45 m 160 84 18: 00 17: 00 2½ 16: 00 15: 00 14: 00 13: 00 12: 00 10: 00 2 11: 00 20 9: 00 Distance from London in miles Q 6 What was the speed for each part of the journey? Time in hours © T Madas
A sales rep drove from London to Manchester, stopping on the way at Birmingham. After his meeting in Manchester, he drove straight to London without a break. His entire journey is shown in the graph below: 240 speed = 220 200 ph 180 140 40 m ph 60 60 h 80 120 100 mp 210 2 120 distance time Miles Hours 210 2½ 420 5 840 10 84 1 90 45 m 160 84 18: 00 17: 00 2½ 16: 00 15: 00 14: 00 13: 00 12: 00 10: 00 2 11: 00 20 9: 00 Distance from London in miles Q 6 What was the speed for each part of the journey? Time in hours © T Madas
 © T Madas
© T Madas
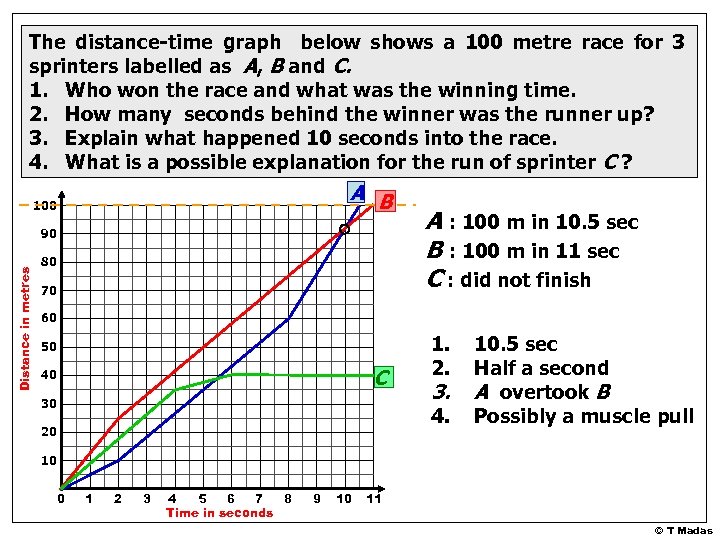 The distance-time graph below shows a 100 metre race for 3 sprinters labelled as A, B and C. 1. Who won the race and what was the winning time. 2. How many seconds behind the winner was the runner up? 3. Explain what happened 10 seconds into the race. 4. What is a possible explanation for the run of sprinter C ? A B 100 Distance in metres 90 80 70 A : 100 m in 10. 5 sec B : 100 m in 11 sec C : did not finish 60 50 C 40 30 1. 2. 3. 4. 20 10. 5 sec Half a second A overtook B Possibly a muscle pull 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 © T Madas
The distance-time graph below shows a 100 metre race for 3 sprinters labelled as A, B and C. 1. Who won the race and what was the winning time. 2. How many seconds behind the winner was the runner up? 3. Explain what happened 10 seconds into the race. 4. What is a possible explanation for the run of sprinter C ? A B 100 Distance in metres 90 80 70 A : 100 m in 10. 5 sec B : 100 m in 11 sec C : did not finish 60 50 C 40 30 1. 2. 3. 4. 20 10. 5 sec Half a second A overtook B Possibly a muscle pull 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 © T Madas
 © T Madas
© T Madas
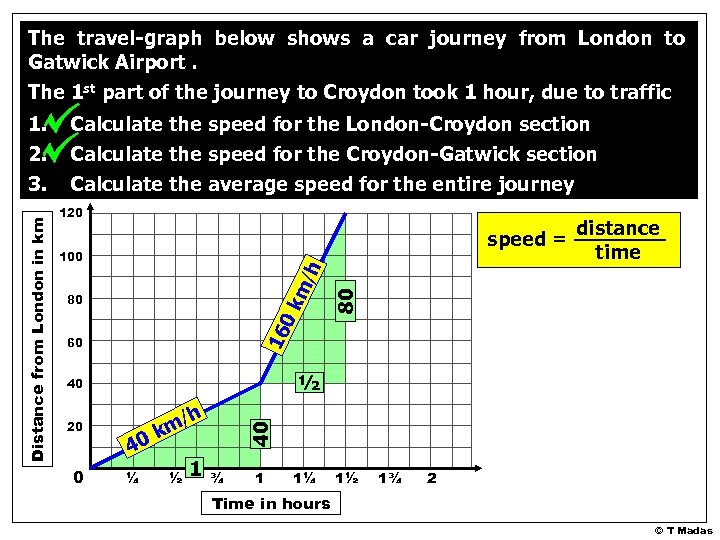 The travel-graph below shows a car journey from London to Gatwick Airport. The 1 st part of the journey to Croydon took 1 hour, due to traffic Calculate the speed for the London-Croydon section Calculate the speed for the Croydon-Gatwick section Calculate the average speed for the entire journey 120 speed = 16 0 80 60 ½ 40 20 0 80 km /h 100 distance time 40 ¼ / km ½ h 1 40 Distance from London in km 1. 2. 3. ¾ 1 1¼ 1½ 1¾ 2 Time in hours © T Madas
The travel-graph below shows a car journey from London to Gatwick Airport. The 1 st part of the journey to Croydon took 1 hour, due to traffic Calculate the speed for the London-Croydon section Calculate the speed for the Croydon-Gatwick section Calculate the average speed for the entire journey 120 speed = 16 0 80 60 ½ 40 20 0 80 km /h 100 distance time 40 ¼ / km ½ h 1 40 Distance from London in km 1. 2. 3. ¾ 1 1¼ 1½ 1¾ 2 Time in hours © T Madas
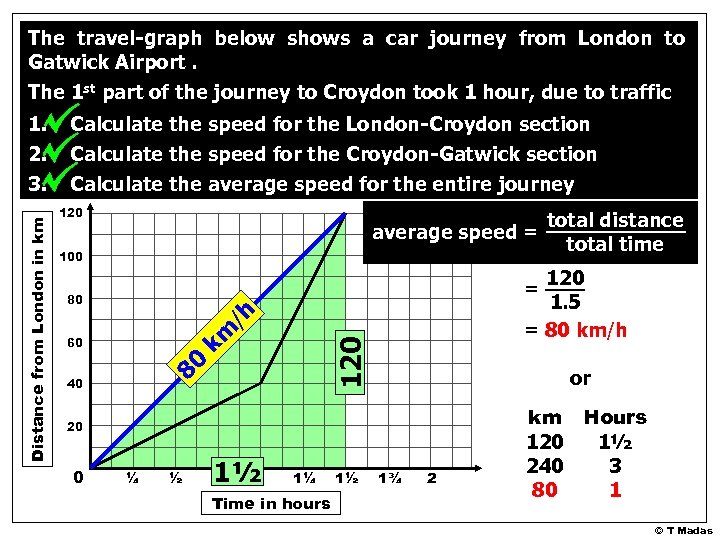 The travel-graph below shows a car journey from London to Gatwick Airport. The 1 st part of the journey to Croydon took 1 hour, due to traffic Calculate the speed for the London-Croydon section Calculate the speed for the Croydon-Gatwick section Calculate the average speed for the entire journey 120 average speed = 100 120 1. 5 = 80 km/h 60 120 km /h 80 40 or 20 0 total distance total time = 80 Distance from London in km 1. 2. 3. ¼ ½ 1½ 1 ¾ 1¼ Time in hours 1½ 1¾ 2 km Hours 120 1½ 240 3 80 1 © T Madas
The travel-graph below shows a car journey from London to Gatwick Airport. The 1 st part of the journey to Croydon took 1 hour, due to traffic Calculate the speed for the London-Croydon section Calculate the speed for the Croydon-Gatwick section Calculate the average speed for the entire journey 120 average speed = 100 120 1. 5 = 80 km/h 60 120 km /h 80 40 or 20 0 total distance total time = 80 Distance from London in km 1. 2. 3. ¼ ½ 1½ 1 ¾ 1¼ Time in hours 1½ 1¾ 2 km Hours 120 1½ 240 3 80 1 © T Madas
 © T Madas
© T Madas
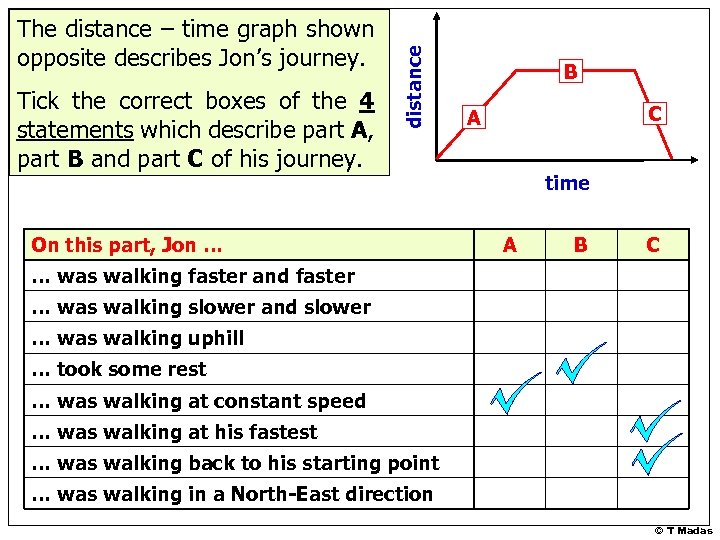 Tick the correct boxes of the 4 statements which describe part A, part B and part C of his journey. distance The distance – time graph shown opposite describes Jon’s journey. On this part, Jon … B C A time A B C … was walking faster and faster … was walking slower and slower … was walking uphill … took some rest … was walking at constant speed … was walking at his fastest … was walking back to his starting point … was walking in a North-East direction © T Madas
Tick the correct boxes of the 4 statements which describe part A, part B and part C of his journey. distance The distance – time graph shown opposite describes Jon’s journey. On this part, Jon … B C A time A B C … was walking faster and faster … was walking slower and slower … was walking uphill … took some rest … was walking at constant speed … was walking at his fastest … was walking back to his starting point … was walking in a North-East direction © T Madas
 © T Madas
© T Madas
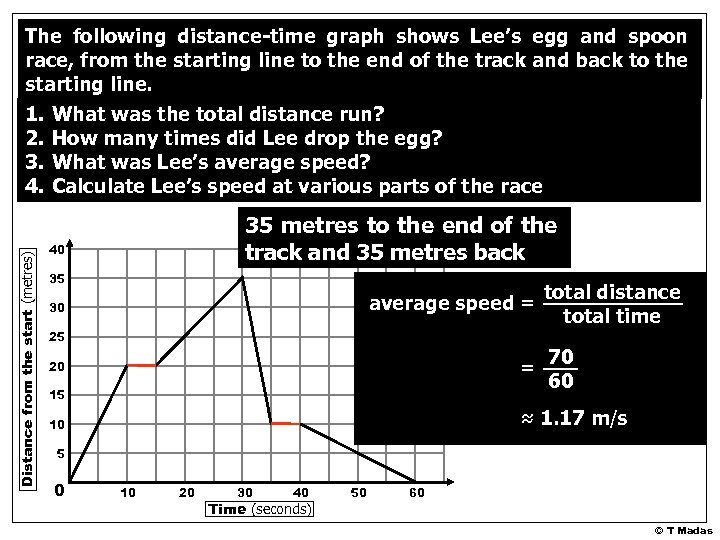 The following distance-time graph shows Lee’s egg and spoon race, from the starting line to the end of the track and back to the starting line. Distance from the start (metres) 1. 2. 3. 4. What was the total distance run? 70 metres How many times did Lee drop the egg? Twice What was Lee’s average speed? approx 1. 17 m/s Calculate Lee’s speed at various parts of the race 35 metres to the end of the track and 35 metres back 40 35 average speed = 30 25 = 20 15 total distance total time 70 60 ≈ 1. 17 m/s 10 5 0 10 20 30 40 Time (seconds) 50 60 © T Madas
The following distance-time graph shows Lee’s egg and spoon race, from the starting line to the end of the track and back to the starting line. Distance from the start (metres) 1. 2. 3. 4. What was the total distance run? 70 metres How many times did Lee drop the egg? Twice What was Lee’s average speed? approx 1. 17 m/s Calculate Lee’s speed at various parts of the race 35 metres to the end of the track and 35 metres back 40 35 average speed = 30 25 = 20 15 total distance total time 70 60 ≈ 1. 17 m/s 10 5 0 10 20 30 40 Time (seconds) 50 60 © T Madas
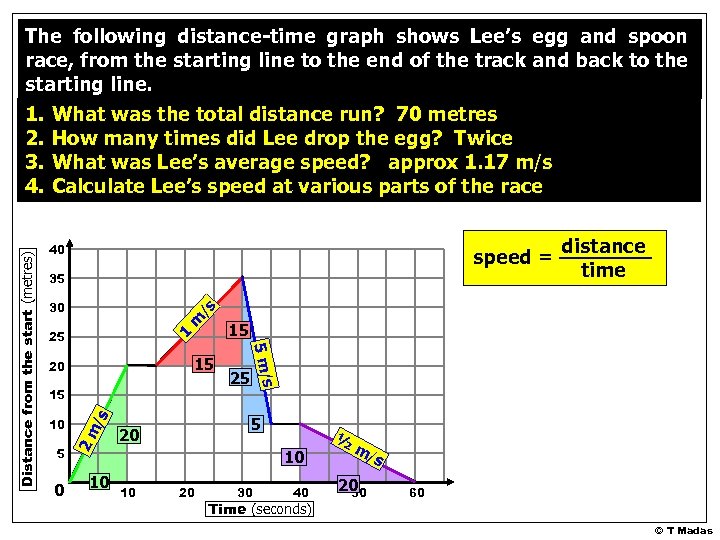 The following distance-time graph shows Lee’s egg and spoon race, from the starting line to the end of the track and back to the starting line. What was the total distance run? 70 metres How many times did Lee drop the egg? Twice What was Lee’s average speed? approx 1. 17 m/s Calculate Lee’s speed at various parts of the race 40 speed = 35 m /s 30 15 20 0 2 m /s 15 5 15 1 25 10 distance time 10 25 5 m /s Distance from the start (metres) 1. 2. 3. 4. 5 20 ½ 10 10 20 30 40 Time (seconds) m/ 20 50 s 60 © T Madas
The following distance-time graph shows Lee’s egg and spoon race, from the starting line to the end of the track and back to the starting line. What was the total distance run? 70 metres How many times did Lee drop the egg? Twice What was Lee’s average speed? approx 1. 17 m/s Calculate Lee’s speed at various parts of the race 40 speed = 35 m /s 30 15 20 0 2 m /s 15 5 15 1 25 10 distance time 10 25 5 m /s Distance from the start (metres) 1. 2. 3. 4. 5 20 ½ 10 10 20 30 40 Time (seconds) m/ 20 50 s 60 © T Madas
 © T Madas
© T Madas
 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
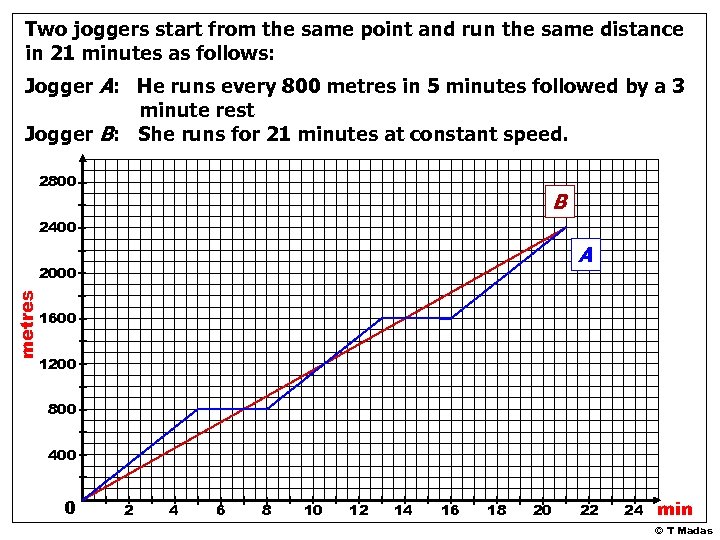 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
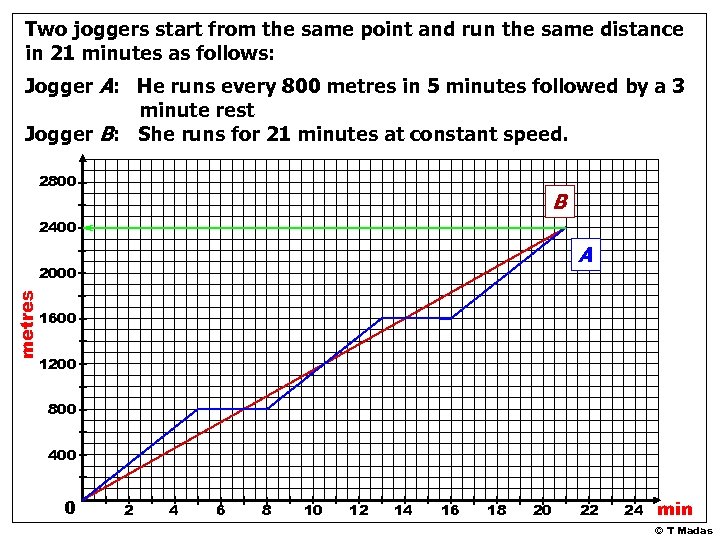 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
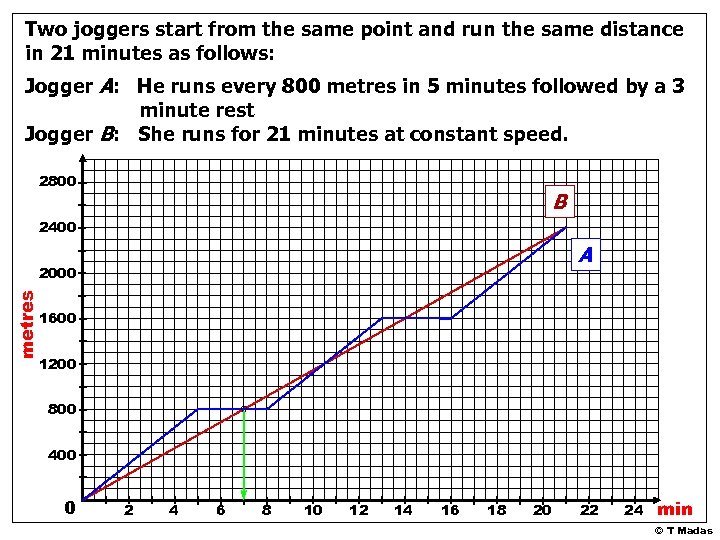 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
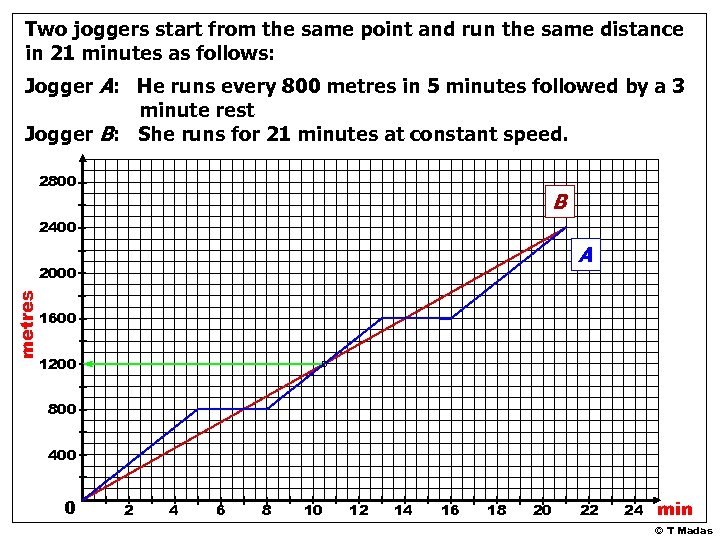 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 2800 B 2400 A metres 2000 1600 1200 800 400 0 2 4 6 8 10 12 14 16 18 20 22 24 min © T Madas
 Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
Two joggers start from the same point and run the same distance in 21 minutes as follows: Jogger A: He runs every 800 metres in 5 minutes followed by a 3 minute rest Jogger B: She runs for 21 minutes at constant speed. 1. Plot a distance-time graph 2. What distance do the joggers cover? 3. After how many minutes does jogger B overtake jogger A for the first time? 4. After how many metres does jogger A overtake jogger B ? © T Madas
 © T Madas
© T Madas
 As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 © T Madas
As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 © T Madas
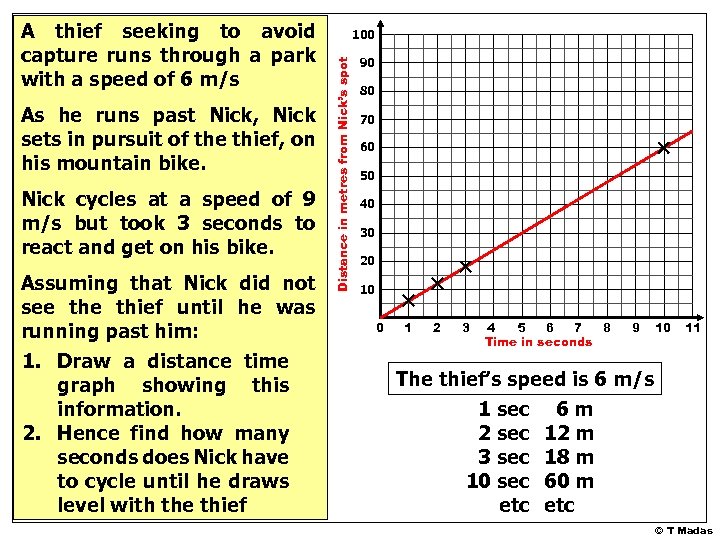 As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 The thief’s speed is 6 m/s 1 sec 6 m 2 sec 12 m 3 sec 18 m 10 sec 60 m etc © T Madas
As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 The thief’s speed is 6 m/s 1 sec 6 m 2 sec 12 m 3 sec 18 m 10 sec 60 m etc © T Madas
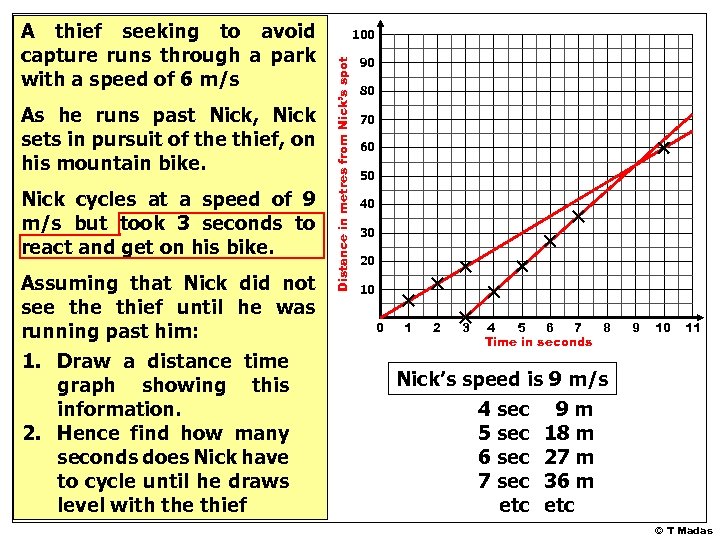 As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 Nick’s speed is 9 m/s 4 1 sec 9 m 5 2 sec 18 m 6 3 sec 27 m 7 4 sec 36 m etc © T Madas
As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 Nick’s speed is 9 m/s 4 1 sec 9 m 5 2 sec 18 m 6 3 sec 27 m 7 4 sec 36 m etc © T Madas
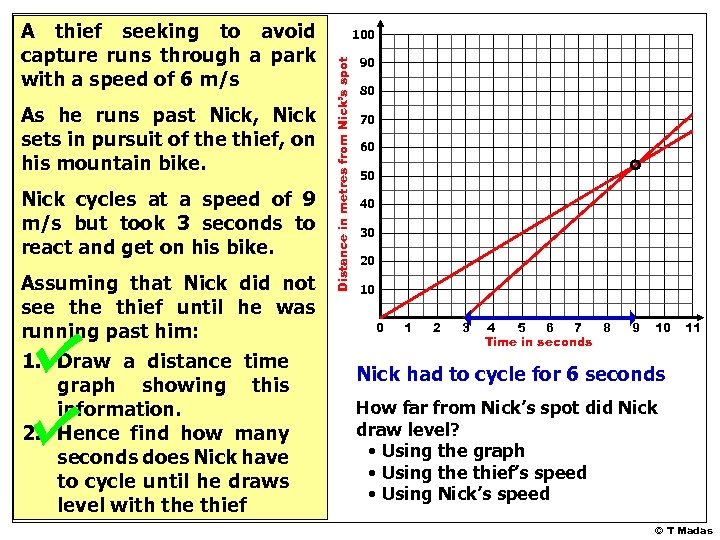 As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 Nick had to cycle for 6 seconds How far from Nick’s spot did Nick draw level? • Using the graph • Using the thief’s speed • Using Nick’s speed © T Madas
As he runs past Nick, Nick sets in pursuit of the thief, on his mountain bike. Nick cycles at a speed of 9 m/s but took 3 seconds to react and get on his bike. Assuming that Nick did not see thief until he was running past him: 1. Draw a distance time graph showing this information. 2. Hence find how many seconds does Nick have to cycle until he draws level with the thief 100 Distance in metres from Nick’s spot A thief seeking to avoid capture runs through a park with a speed of 6 m/s 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 Time in seconds 9 10 11 Nick had to cycle for 6 seconds How far from Nick’s spot did Nick draw level? • Using the graph • Using the thief’s speed • Using Nick’s speed © T Madas
 © T Madas
© T Madas
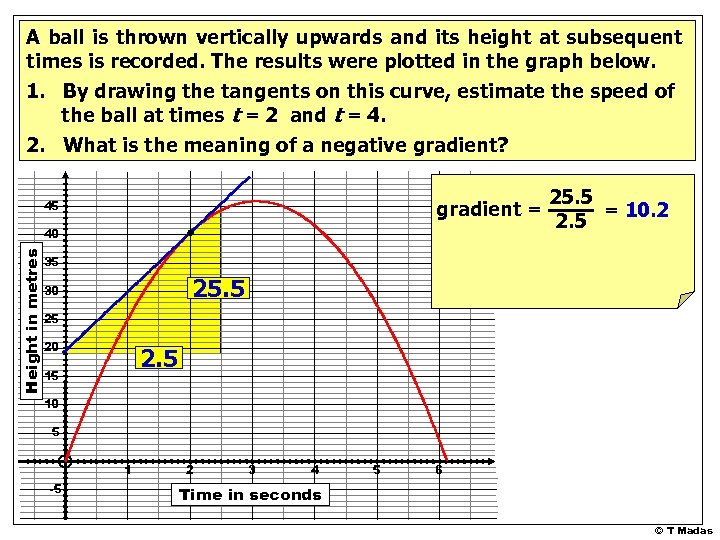 A ball is thrown vertically upwards and its height at subsequent times is recorded. The results were plotted in the graph below. 1. By drawing the tangents on this curve, estimate the speed of the ball at times t = 2 and t = 4. 2. What is the meaning of a negative gradient? gradient = 45 Height in metres 40 25. 5 = 10. 2 2. 5 35 25. 5 30 25 20 2. 5 15 10 5 1 -5 2 3 4 5 6 Time in seconds © T Madas
A ball is thrown vertically upwards and its height at subsequent times is recorded. The results were plotted in the graph below. 1. By drawing the tangents on this curve, estimate the speed of the ball at times t = 2 and t = 4. 2. What is the meaning of a negative gradient? gradient = 45 Height in metres 40 25. 5 = 10. 2 2. 5 35 25. 5 30 25 20 2. 5 15 10 5 1 -5 2 3 4 5 6 Time in seconds © T Madas
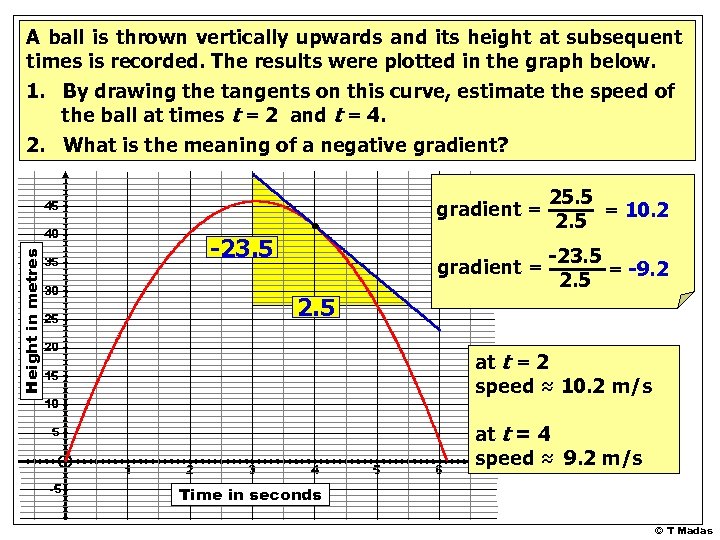 A ball is thrown vertically upwards and its height at subsequent times is recorded. The results were plotted in the graph below. 1. By drawing the tangents on this curve, estimate the speed of the ball at times t = 2 and t = 4. 2. What is the meaning of a negative gradient? gradient = Height in metres 40 -23. 5 35 30 25. 5 = 10. 2 2. 5 gradient = 45 -23. 5 = -9. 2 2. 5 25 20 at t = 2 speed ≈ 10. 2 m/s 15 10 5 1 -5 2 3 4 5 6 at t = 4 speed ≈ 9. 2 m/s Time in seconds © T Madas
A ball is thrown vertically upwards and its height at subsequent times is recorded. The results were plotted in the graph below. 1. By drawing the tangents on this curve, estimate the speed of the ball at times t = 2 and t = 4. 2. What is the meaning of a negative gradient? gradient = Height in metres 40 -23. 5 35 30 25. 5 = 10. 2 2. 5 gradient = 45 -23. 5 = -9. 2 2. 5 25 20 at t = 2 speed ≈ 10. 2 m/s 15 10 5 1 -5 2 3 4 5 6 at t = 4 speed ≈ 9. 2 m/s Time in seconds © T Madas
 © T Madas
© T Madas
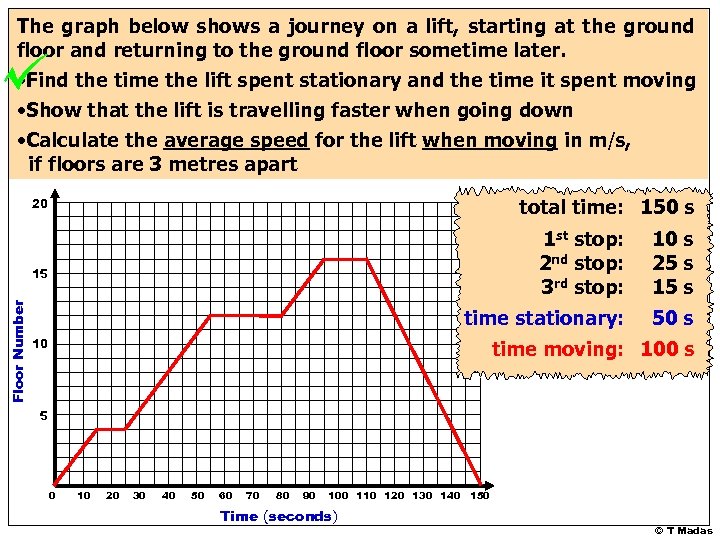 The graph below shows a journey on a lift, starting at the ground floor and returning to the ground floor sometime later. • Find the time the lift spent stationary and the time it spent moving • Show that the lift is travelling faster when going down • Calculate the average speed for the lift when moving in m/s, if floors are 3 metres apart total time: 150 s 20 1 st stop: 2 nd stop: 3 rd stop: 10 s 25 s 15 s time stationary: 50 s Floor Number 15 10 time moving: 100 s 5 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 Time (seconds) © T Madas
The graph below shows a journey on a lift, starting at the ground floor and returning to the ground floor sometime later. • Find the time the lift spent stationary and the time it spent moving • Show that the lift is travelling faster when going down • Calculate the average speed for the lift when moving in m/s, if floors are 3 metres apart total time: 150 s 20 1 st stop: 2 nd stop: 3 rd stop: 10 s 25 s 15 s time stationary: 50 s Floor Number 15 10 time moving: 100 s 5 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 Time (seconds) © T Madas
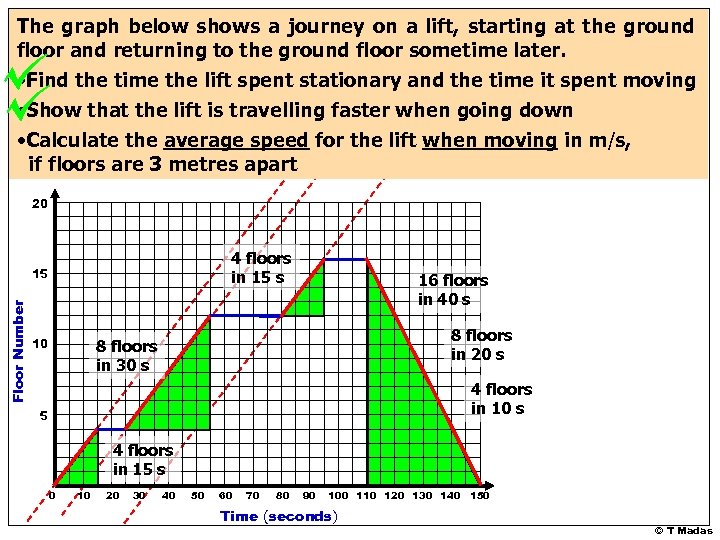 The graph below shows a journey on a lift, starting at the ground floor and returning to the ground floor sometime later. • Find the time the lift spent stationary and the time it spent moving • Show that the lift is travelling faster when going down • Calculate the average speed for the lift when moving in m/s, if floors are 3 metres apart 20 4 floors in 15 s Floor Number 15 10 16 floors in 40 s 8 floors in 20 s 8 floors in 30 s 4 floors in 10 s 5 4 floors in 15 s 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 Time (seconds) © T Madas
The graph below shows a journey on a lift, starting at the ground floor and returning to the ground floor sometime later. • Find the time the lift spent stationary and the time it spent moving • Show that the lift is travelling faster when going down • Calculate the average speed for the lift when moving in m/s, if floors are 3 metres apart 20 4 floors in 15 s Floor Number 15 10 16 floors in 40 s 8 floors in 20 s 8 floors in 30 s 4 floors in 10 s 5 4 floors in 15 s 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 Time (seconds) © T Madas
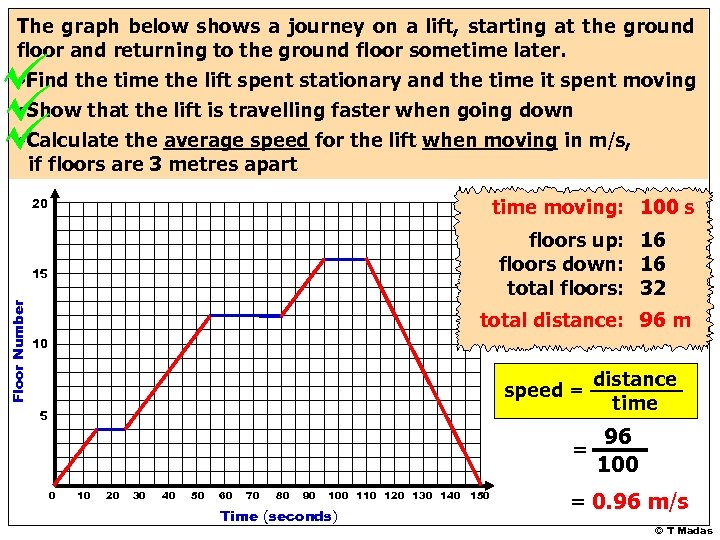 The graph below shows a journey on a lift, starting at the ground floor and returning to the ground floor sometime later. • Find the time the lift spent stationary and the time it spent moving • Show that the lift is travelling faster when going down • Calculate the average speed for the lift when moving in m/s, if floors are 3 metres apart time moving: 100 s 20 floors up: 16 floors down: 16 total floors: 32 Floor Number 15 total distance: 96 m 10 speed = 5 = 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 Time (seconds) distance time 96 100 = 0. 96 m/s © T Madas
The graph below shows a journey on a lift, starting at the ground floor and returning to the ground floor sometime later. • Find the time the lift spent stationary and the time it spent moving • Show that the lift is travelling faster when going down • Calculate the average speed for the lift when moving in m/s, if floors are 3 metres apart time moving: 100 s 20 floors up: 16 floors down: 16 total floors: 32 Floor Number 15 total distance: 96 m 10 speed = 5 = 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 Time (seconds) distance time 96 100 = 0. 96 m/s © T Madas
 © T Madas
© T Madas


