Т Е Н И ПОСТРОЕНИЕ ТЕНЕЙ В ОРТОГОНАЛЬНЫХ






12424-teni_v_axonometrii.ppt
- Количество слайдов: 19
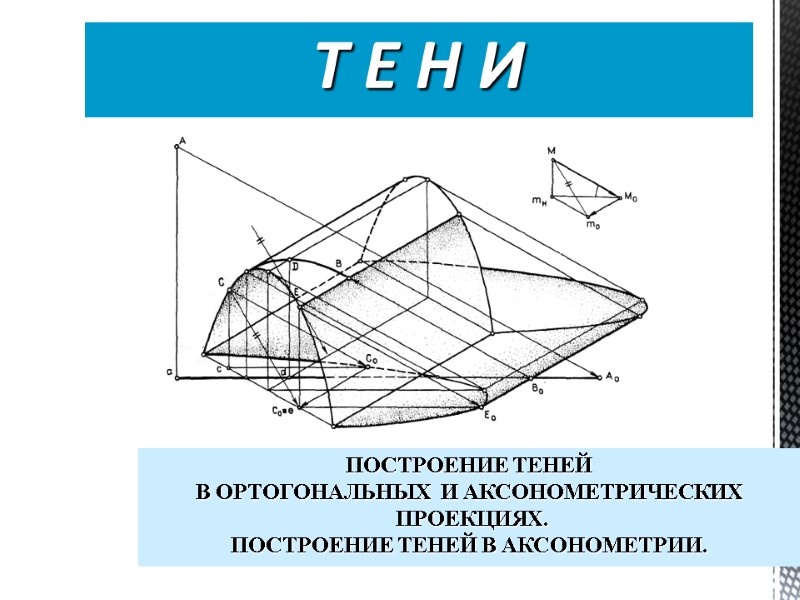
 Т Е Н И ПОСТРОЕНИЕ ТЕНЕЙ В ОРТОГОНАЛЬНЫХ И АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЯХ. ПОСТРОЕНИЕ ТЕНЕЙ В АКСОНОМЕТРИИ.
Т Е Н И ПОСТРОЕНИЕ ТЕНЕЙ В ОРТОГОНАЛЬНЫХ И АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЯХ. ПОСТРОЕНИЕ ТЕНЕЙ В АКСОНОМЕТРИИ.
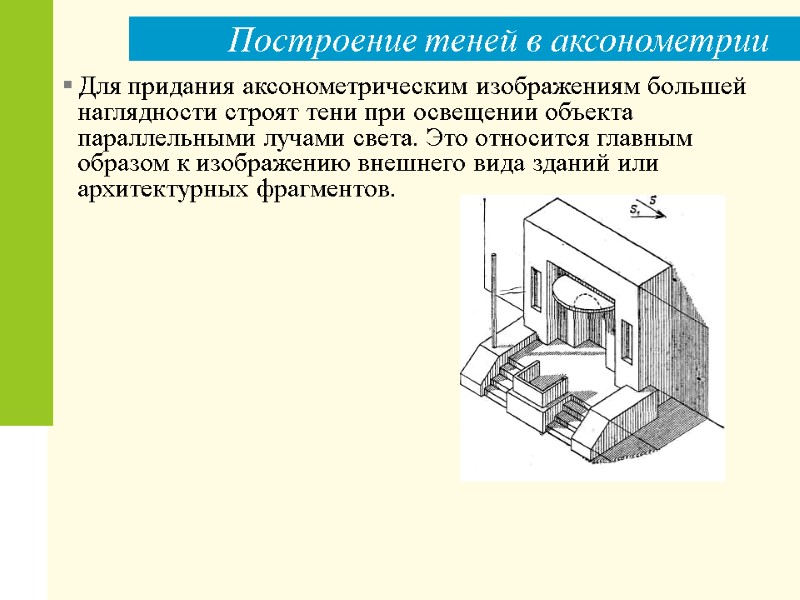
 Построение теней в аксонометрии Для придания аксонометрическим изображениям большей наглядности строят тени при освещении объекта параллельными лучами света. Это относится главным образом к изображению внешнего вида зданий или архитектурных фрагментов.
Построение теней в аксонометрии Для придания аксонометрическим изображениям большей наглядности строят тени при освещении объекта параллельными лучами света. Это относится главным образом к изображению внешнего вида зданий или архитектурных фрагментов.
 ТЕНИ В АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЯХ При построении теней в аксонометрических проекциях направление световых лучей может быть принято и задается аксонометрическим световым лучом и одной из его вторичных проекций. Направление лучей света чаще всего принимается от солнца (световые лучи взаимно параллельны). Направление световых лучей выбирается с учетом получения светотеневого рисунка, выявляющий наилучшим образом объемный рельеф, конфигурацию здания или сооружения и придания чертежу наибольшей выразительности. Основные положения, рассмотренные при построении теней в ортогональных проекциях, остаются в силе и при построении теней в аксонометрии. В аксонометрических проекциях направление световых лучей берется произвольно, но с соблюдением условий правдоподобности освещения.
ТЕНИ В АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЯХ При построении теней в аксонометрических проекциях направление световых лучей может быть принято и задается аксонометрическим световым лучом и одной из его вторичных проекций. Направление лучей света чаще всего принимается от солнца (световые лучи взаимно параллельны). Направление световых лучей выбирается с учетом получения светотеневого рисунка, выявляющий наилучшим образом объемный рельеф, конфигурацию здания или сооружения и придания чертежу наибольшей выразительности. Основные положения, рассмотренные при построении теней в ортогональных проекциях, остаются в силе и при построении теней в аксонометрии. В аксонометрических проекциях направление световых лучей берется произвольно, но с соблюдением условий правдоподобности освещения.
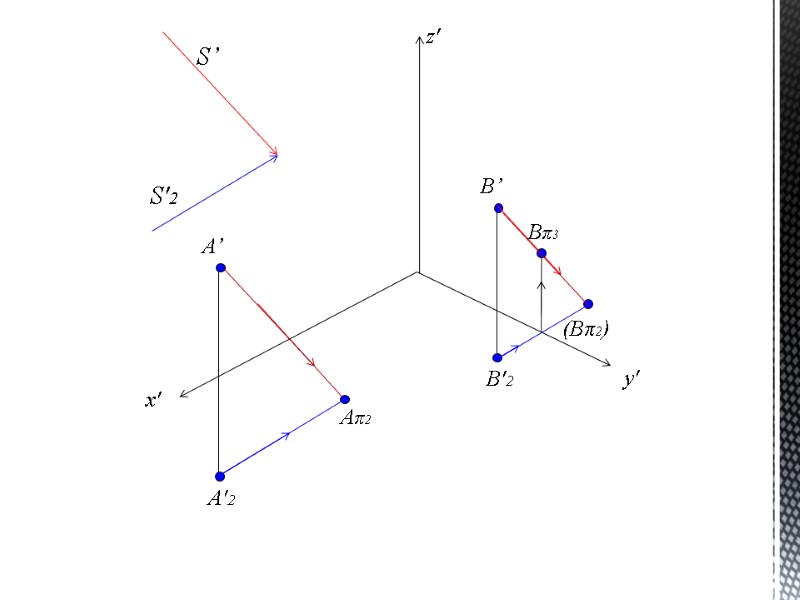
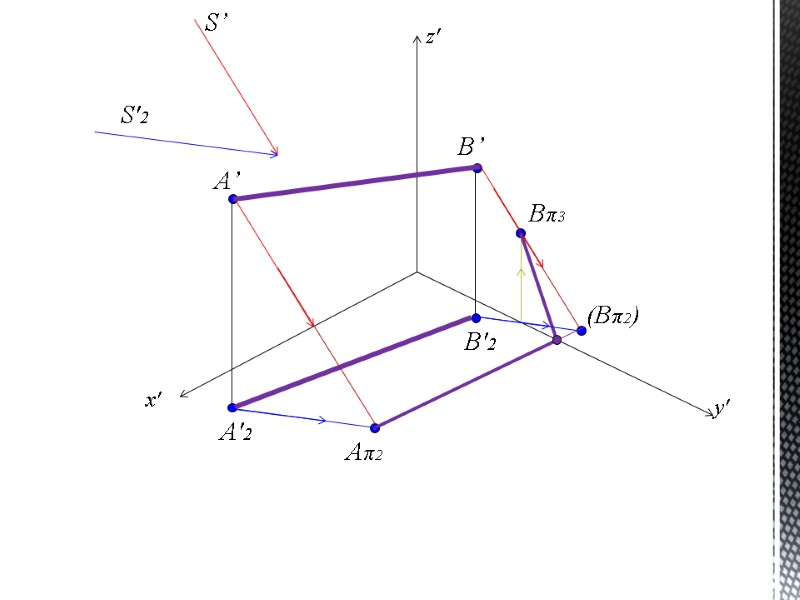
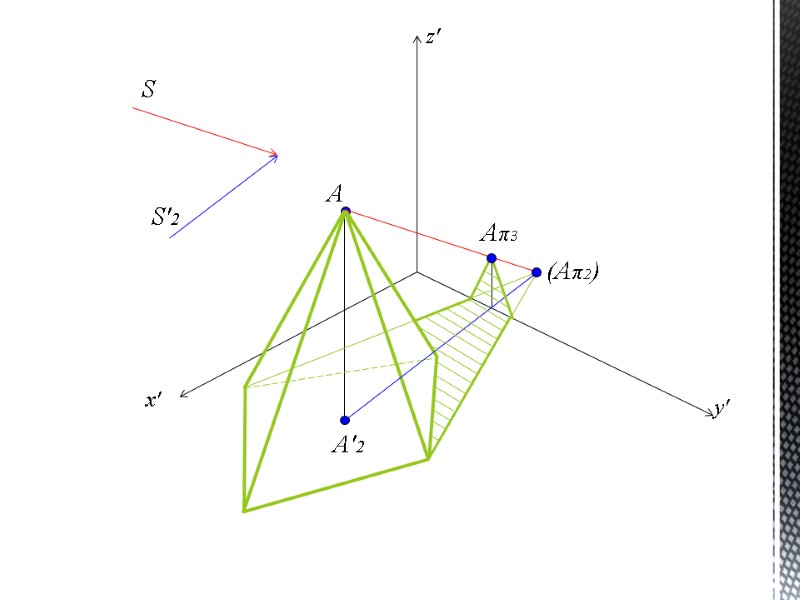
 ТЕНЬ ОТ ТОЧКИ И ПРЯМОЙ На рисунке даны: точка А – точка в аксонометрии и ее горизонтальная проекция А2. Направление световых лучей задаем аксонометрическим световым лучом s и его горизонтальной проекцией – s2. Для построения падающей тени от точки А проводим через эту точку световой луч принятого направления т.е. через точку в аксонометрии проводим аксонометрический луч, а через горизонтальную проекцию точки – луч, параллельный горизонтальной проекции светового луча. Точка пересечения светового луча с плоскостью или поверхностью и будет являться падающей тенью от данной точки. На рисунке тень от точки А падает на горизонтальную плоскость проекций, а тень от точки В на фронтальную плоскость проекций.
ТЕНЬ ОТ ТОЧКИ И ПРЯМОЙ На рисунке даны: точка А – точка в аксонометрии и ее горизонтальная проекция А2. Направление световых лучей задаем аксонометрическим световым лучом s и его горизонтальной проекцией – s2. Для построения падающей тени от точки А проводим через эту точку световой луч принятого направления т.е. через точку в аксонометрии проводим аксонометрический луч, а через горизонтальную проекцию точки – луч, параллельный горизонтальной проекции светового луча. Точка пересечения светового луча с плоскостью или поверхностью и будет являться падающей тенью от данной точки. На рисунке тень от точки А падает на горизонтальную плоскость проекций, а тень от точки В на фронтальную плоскость проекций.
 x' y' z' A’ A'2 B’ B'2 S’ S'2 Aπ2 (Bπ2) Bπ3
x' y' z' A’ A'2 B’ B'2 S’ S'2 Aπ2 (Bπ2) Bπ3
 x' y' z' A’ A'2 B’ B'2 S’ S'2 Aπ2 (Bπ2) Bπ3
x' y' z' A’ A'2 B’ B'2 S’ S'2 Aπ2 (Bπ2) Bπ3
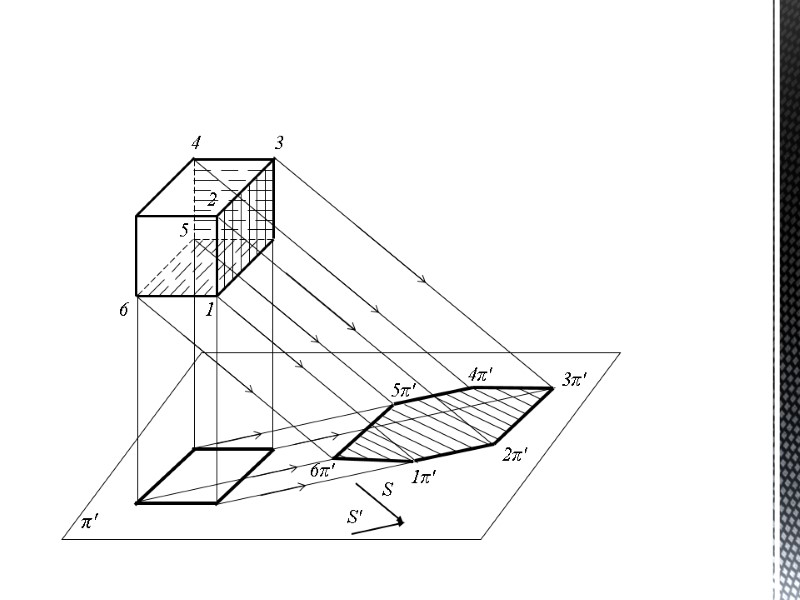
 ТЕНИ ГЕОМЕТРИЧЕСКИХ ТЕЛ При построении теней геометрических тел определяются контуры как собственных, так и падающих теней. Так как контур падающей тени строится в зависимости от контура собственной тени, то в первую очередь следует определить контуры собственной тени.
ТЕНИ ГЕОМЕТРИЧЕСКИХ ТЕЛ При построении теней геометрических тел определяются контуры как собственных, так и падающих теней. Так как контур падающей тени строится в зависимости от контура собственной тени, то в первую очередь следует определить контуры собственной тени.
 4 3 2 1 6 5 S S' 5π' π' 3π' 4π' 2π' 1π' 6π'
4 3 2 1 6 5 S S' 5π' π' 3π' 4π' 2π' 1π' 6π'
 x' y' z' A A'2 S S'2 (Aπ2) Aπ3
x' y' z' A A'2 S S'2 (Aπ2) Aπ3


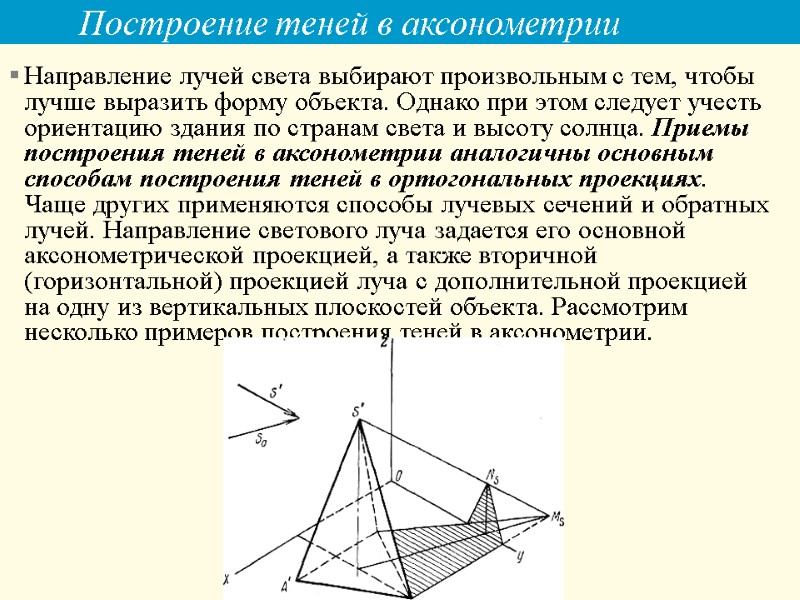
 Построение теней в аксонометрии Направление лучей света выбирают произвольным с тем, чтобы лучше выразить форму объекта. Однако при этом следует учесть ориентацию здания по странам света и высоту солнца. Приемы построения теней в аксонометрии аналогичны основным способам построения теней в ортогональных проекциях. Чаще других применяются способы лучевых сечений и обратных лучей. Направление светового луча задается его основной аксонометрической проекцией, а также вторичной (горизонтальной) проекцией луча с дополнительной проекцией на одну из вертикальных плоскостей объекта. Рассмотрим несколько примеров построения теней в аксонометрии.
Построение теней в аксонометрии Направление лучей света выбирают произвольным с тем, чтобы лучше выразить форму объекта. Однако при этом следует учесть ориентацию здания по странам света и высоту солнца. Приемы построения теней в аксонометрии аналогичны основным способам построения теней в ортогональных проекциях. Чаще других применяются способы лучевых сечений и обратных лучей. Направление светового луча задается его основной аксонометрической проекцией, а также вторичной (горизонтальной) проекцией луча с дополнительной проекцией на одну из вертикальных плоскостей объекта. Рассмотрим несколько примеров построения теней в аксонометрии.
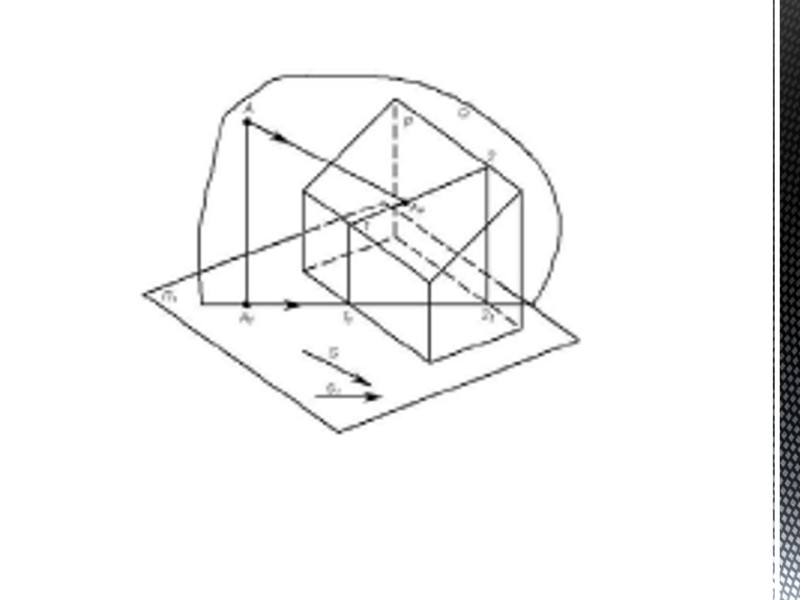
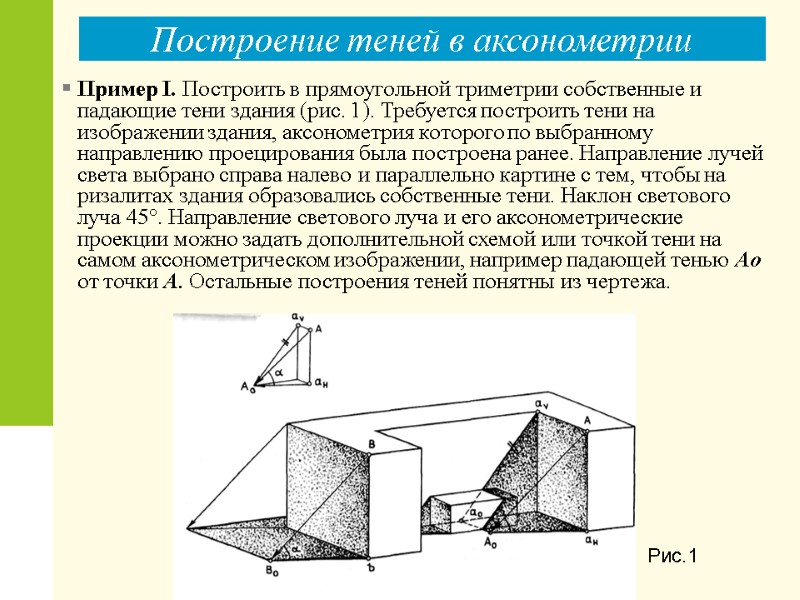
 Построение теней в аксонометрии Пример I. Построить в прямоугольной триметрии собственные и падающие тени здания (рис. 1). Требуется построить тени на изображении здания, аксонометрия которого по выбранному направлению проецирования была построена ранее. Направление лучей света выбрано справа налево и параллельно картине с тем, чтобы на ризалитах здания образовались собственные тени. Наклон светового луча 45°. Направление светового луча и его аксонометрические проекции можно задать дополнительной схемой или точкой тени на самом аксонометрическом изображении, например падающей тенью Ао от точки А. Остальные построения теней понятны из чертежа. Рис.1
Построение теней в аксонометрии Пример I. Построить в прямоугольной триметрии собственные и падающие тени здания (рис. 1). Требуется построить тени на изображении здания, аксонометрия которого по выбранному направлению проецирования была построена ранее. Направление лучей света выбрано справа налево и параллельно картине с тем, чтобы на ризалитах здания образовались собственные тени. Наклон светового луча 45°. Направление светового луча и его аксонометрические проекции можно задать дополнительной схемой или точкой тени на самом аксонометрическом изображении, например падающей тенью Ао от точки А. Остальные построения теней понятны из чертежа. Рис.1
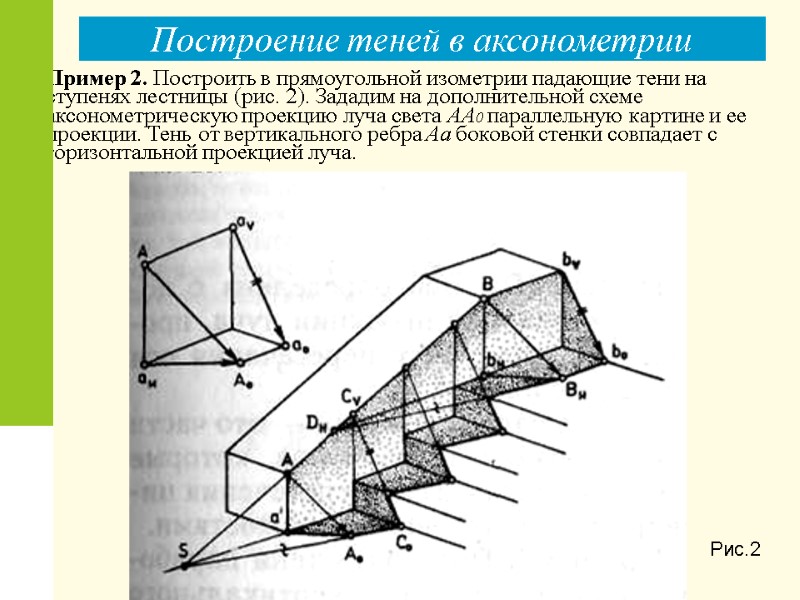
 Построение теней в аксонометрии Пример 2. Построить в прямоугольной изометрии падающие тени на ступенях лестницы (рис. 2). Зададим на дополнительной схеме аксонометрическую проекцию луча света АА0 параллельную картине и ее проекции. Тень от вертикального ребра Аа боковой стенки совпадает с горизонтальной проекцией луча. Рис.2
Построение теней в аксонометрии Пример 2. Построить в прямоугольной изометрии падающие тени на ступенях лестницы (рис. 2). Зададим на дополнительной схеме аксонометрическую проекцию луча света АА0 параллельную картине и ее проекции. Тень от вертикального ребра Аа боковой стенки совпадает с горизонтальной проекцией луча. Рис.2
 Построение теней в аксонометрии Тень от наклонного ребра на горизонтальной плоскости построена на основе родственного соответствия между вертикальной плоскостью боковой стенки и горизонтальной плоскостью. Осью родства является прямая Sa', а родственными точками — точки А и ее тень Ао. Тени на горизонтальных плоскостях (проступях) ступеней будут параллельны построенному контуру падающей тени — отрезку А0С0. Контуры теней на вертикальных плоскостях (подступенках) построены с помощью проекции луча на фронтальной плоскости, параллельно проекции луча ava0 на дополнительной схеме. Рис. 2
Построение теней в аксонометрии Тень от наклонного ребра на горизонтальной плоскости построена на основе родственного соответствия между вертикальной плоскостью боковой стенки и горизонтальной плоскостью. Осью родства является прямая Sa', а родственными точками — точки А и ее тень Ао. Тени на горизонтальных плоскостях (проступях) ступеней будут параллельны построенному контуру падающей тени — отрезку А0С0. Контуры теней на вертикальных плоскостях (подступенках) построены с помощью проекции луча на фронтальной плоскости, параллельно проекции луча ava0 на дополнительной схеме. Рис. 2
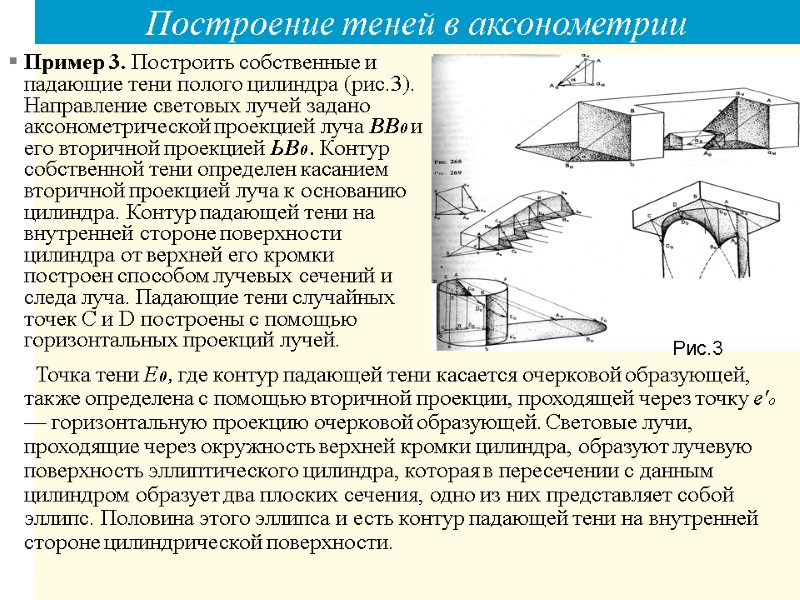
 Построение теней в аксонометрии Пример 3. Построить собственные и падающие тени полого цилиндра (рис.3). Направление световых лучей задано аксонометрической проекцией луча ВВ0 и его вторичной проекцией ЬВ0 . Контур собственной тени определен касанием вторичной проекцией луча к основанию цилиндра. Контур падающей тени на внутренней стороне поверхности цилиндра от верхней его кромки построен способом лучевых сечений и следа луча. Падающие тени случайных точек С и D построены с помощью горизонтальных проекций лучей. Точка тени Е0 , где контур падающей тени касается очерковой образующей, также определена с помощью вторичной проекции, проходящей через точку е'о — горизонтальную проекцию очерковой образующей. Световые лучи, проходящие через окружность верхней кромки цилиндра, образуют лучевую поверхность эллиптического цилиндра, которая в пересечении с данным цилиндром образует два плоских сечения, одно из них представляет собой эллипс. Половина этого эллипса и есть контур падающей тени на внутренней стороне цилиндрической поверхности. Рис.3
Построение теней в аксонометрии Пример 3. Построить собственные и падающие тени полого цилиндра (рис.3). Направление световых лучей задано аксонометрической проекцией луча ВВ0 и его вторичной проекцией ЬВ0 . Контур собственной тени определен касанием вторичной проекцией луча к основанию цилиндра. Контур падающей тени на внутренней стороне поверхности цилиндра от верхней его кромки построен способом лучевых сечений и следа луча. Падающие тени случайных точек С и D построены с помощью горизонтальных проекций лучей. Точка тени Е0 , где контур падающей тени касается очерковой образующей, также определена с помощью вторичной проекции, проходящей через точку е'о — горизонтальную проекцию очерковой образующей. Световые лучи, проходящие через окружность верхней кромки цилиндра, образуют лучевую поверхность эллиптического цилиндра, которая в пересечении с данным цилиндром образует два плоских сечения, одно из них представляет собой эллипс. Половина этого эллипса и есть контур падающей тени на внутренней стороне цилиндрической поверхности. Рис.3
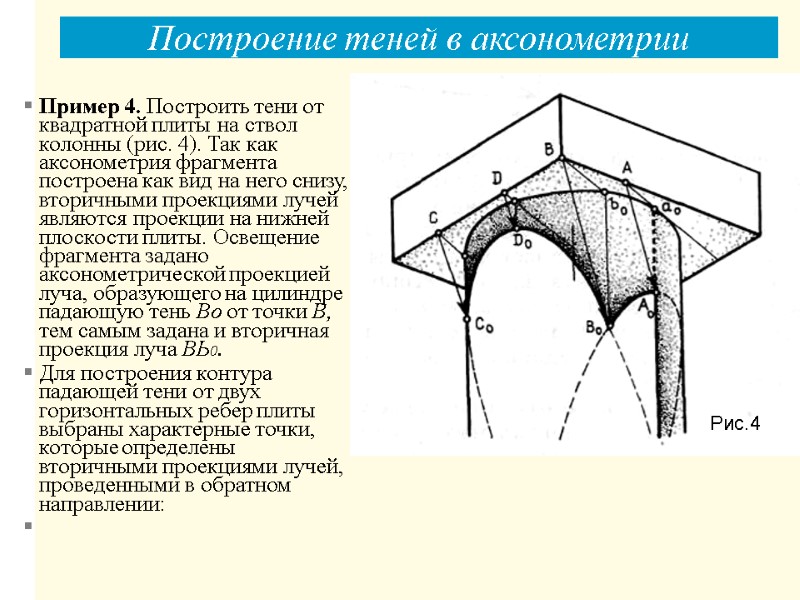
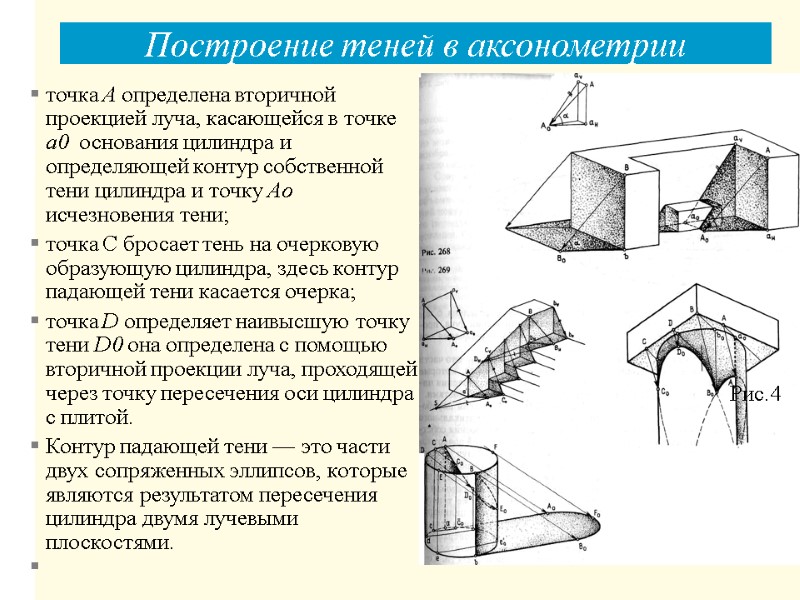
 Построение теней в аксонометрии Пример 4. Построить тени от квадратной плиты на ствол колонны (рис. 4). Так как аксонометрия фрагмента построена как вид на него снизу, вторичными проекциями лучей являются проекции на нижней плоскости плиты. Освещение фрагмента задано аксонометрической проекцией луча, образующего на цилиндре падающую тень Во от точки В, тем самым задана и вторичная проекция луча ВЬ0. Для построения контура падающей тени от двух горизонтальных ребер плиты выбраны характерные точки, которые определены вторичными проекциями лучей, проведенными в обратном направлении: Рис.4
Построение теней в аксонометрии Пример 4. Построить тени от квадратной плиты на ствол колонны (рис. 4). Так как аксонометрия фрагмента построена как вид на него снизу, вторичными проекциями лучей являются проекции на нижней плоскости плиты. Освещение фрагмента задано аксонометрической проекцией луча, образующего на цилиндре падающую тень Во от точки В, тем самым задана и вторичная проекция луча ВЬ0. Для построения контура падающей тени от двух горизонтальных ребер плиты выбраны характерные точки, которые определены вторичными проекциями лучей, проведенными в обратном направлении: Рис.4
 точка А определена вторичной проекцией луча, касающейся в точке а0 основания цилиндра и определяющей контур собственной тени цилиндра и точку Ао исчезновения тени; точка С бросает тень на очерковую образующую цилиндра, здесь контур падающей тени касается очерка; точка D определяет наивысшую точку тени D0 она определена с помощью вторичной проекции луча, проходящей через точку пересечения оси цилиндра с плитой. Контур падающей тени — это части двух сопряженных эллипсов, которые являются результатом пересечения цилиндра двумя лучевыми плоскостями. Рис.4 Построение теней в аксонометрии
точка А определена вторичной проекцией луча, касающейся в точке а0 основания цилиндра и определяющей контур собственной тени цилиндра и точку Ао исчезновения тени; точка С бросает тень на очерковую образующую цилиндра, здесь контур падающей тени касается очерка; точка D определяет наивысшую точку тени D0 она определена с помощью вторичной проекции луча, проходящей через точку пересечения оси цилиндра с плитой. Контур падающей тени — это части двух сопряженных эллипсов, которые являются результатом пересечения цилиндра двумя лучевыми плоскостями. Рис.4 Построение теней в аксонометрии
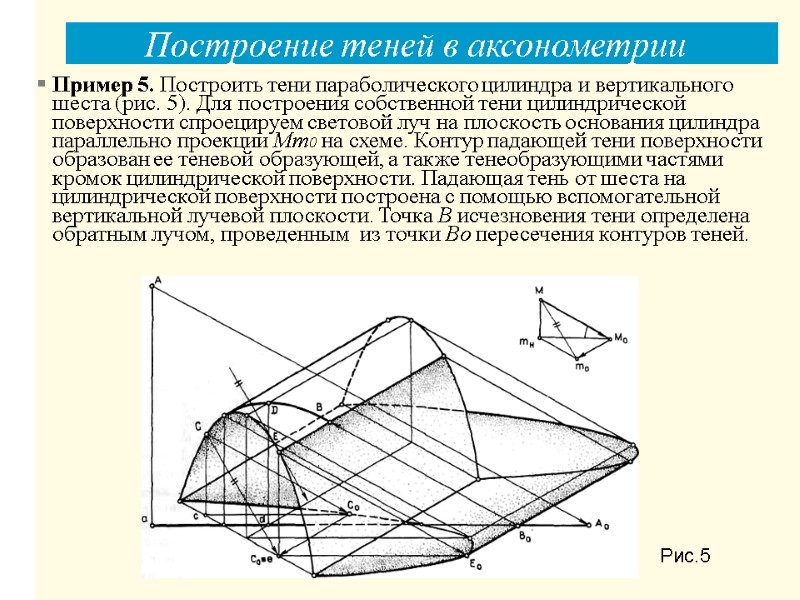
 Построение теней в аксонометрии Рис.5 Пример 5. Построить тени параболического цилиндра и вертикального шеста (рис. 5). Для построения собственной тени цилиндрической поверхности спроецируем световой луч на плоскость основания цилиндра параллельно проекции Мт0 на схеме. Контур падающей тени поверхности образован ее теневой образующей, а также тенеобразующими частями кромок цилиндрической поверхности. Падающая тень от шеста на цилиндрической поверхности построена с помощью вспомогательной вертикальной лучевой плоскости. Точка В исчезновения тени определена обратным лучом, проведенным из точки Во пересечения контуров теней.
Построение теней в аксонометрии Рис.5 Пример 5. Построить тени параболического цилиндра и вертикального шеста (рис. 5). Для построения собственной тени цилиндрической поверхности спроецируем световой луч на плоскость основания цилиндра параллельно проекции Мт0 на схеме. Контур падающей тени поверхности образован ее теневой образующей, а также тенеобразующими частями кромок цилиндрической поверхности. Падающая тень от шеста на цилиндрической поверхности построена с помощью вспомогательной вертикальной лучевой плоскости. Точка В исчезновения тени определена обратным лучом, проведенным из точки Во пересечения контуров теней.

