Systems Of Linear Equations and other stuff

Systems Of Linear Equations … and other stuff

Please select a Team. 1. 2. 3. 4. 5. 1 Team 2 Team 3 Team 4 Team 5 2 3 4 5

Tell whether the system has no solution, one solution, or infinitely many solutions.

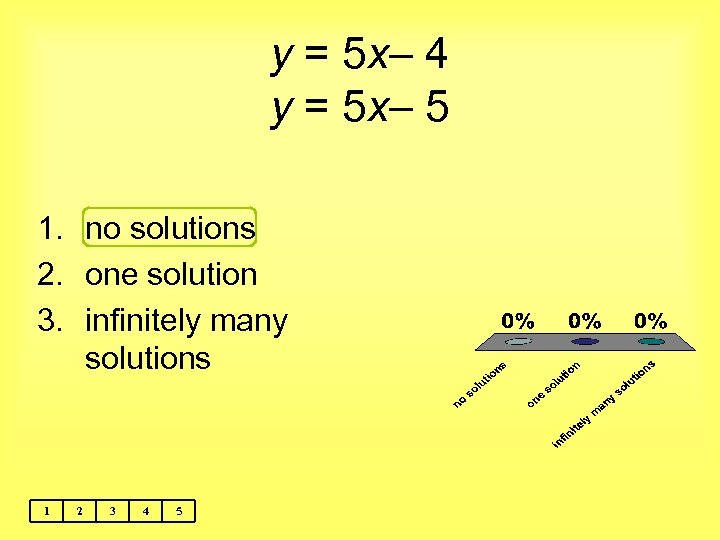y = 5 x– 4 y = 5 x– 5 1. no solutions 2. one solution 3. infinitely many solutions 1 2 3 4 5

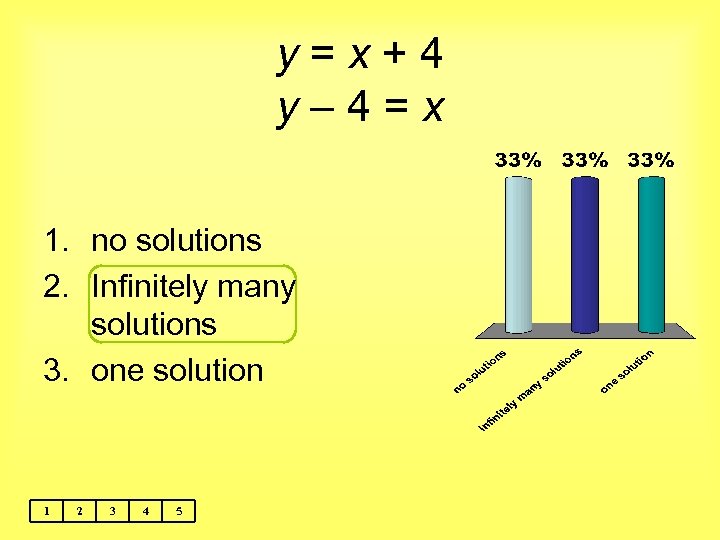y=x+4 y– 4=x 1. no solutions 2. Infinitely many solutions 3. one solution 1 2 3 4 5

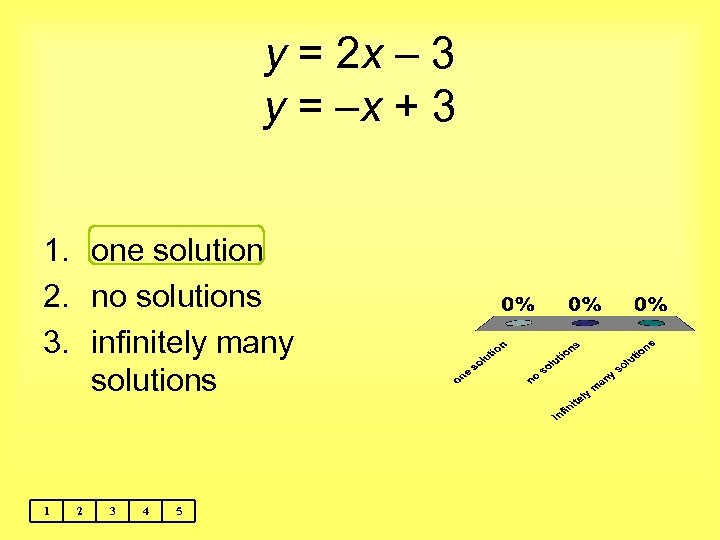y = 2 x – 3 y = –x + 3 1. one solution 2. no solutions 3. infinitely many solutions 1 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

Solve the following systems of equations. . … if you can.

y = 2 x + 3 y = 3 x + 1 1. 2. 3. 4. 1 (– 2, – 1) (– 1, – 2) (2, 7) (– 2, – 5) 2 3 4 5

Solve by substitution. y = 2 x – 10 y = 4 x – 8 1. 2. 3. 4. 1 (3, 4) (– 1, – 12) (– 4, – 17) (3, – 4) 2 3 4 5

3 y = –x + 2 y = –x + 9 1. 2. 3. 4. 1 (3, 6) (20, – 4) (10, – 1) (– 1, 8) 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

y = 4 x + 6 y = 2 x 1. 2. 3. 4. 1 (1, 2) (3, 6) (6, 3) (-3, -6) 2 3 4 5

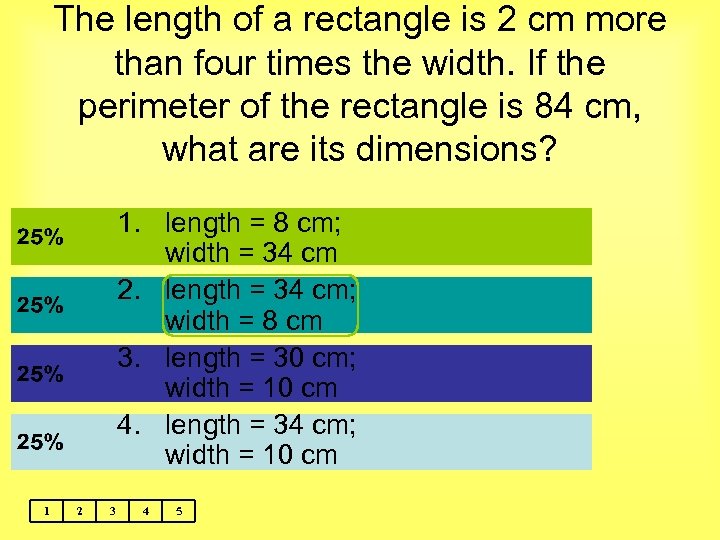The length of a rectangle is 2 cm more than four times the width. If the perimeter of the rectangle is 84 cm, what are its dimensions? 1. length = 8 cm; width = 34 cm 2. length = 34 cm; width = 8 cm 3. length = 30 cm; width = 10 cm 4. length = 34 cm; width = 10 cm 1 2 3 4 5

Find the value of b that makes the system of equations have the solution (3, 5). y = 3 x – 4 y = bx + 2 1. 2. 3. 4. 1 2 3 0 – 1 2 1 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

The sum of two numbers is 82. Their difference is 24. Write a system of equations that describes this situation. 1. x + y = 8 – y = 24 2. x – y = 8 2 x + y = 24 3. x + y = 24 – x = 82 4. x + y = 8 – y = 24 1 2 3 4 5 2 x 48 and 24 52 and 30 y 48 and 30 2 x 53 and 29

Sharon has some one-dollar bills and some five -dollar bills. She has 14 bills. The value of the bills is $30. Solve a system of equations using elimination to find how many of each kind of bill she has. 1. 2. 3. 4. 1 2 3 4 five-dollar bills, 10 one-dollar bills 3 five-dollar bills, 10 one-dollar bills 5 five-dollar bills, 5 one-dollar bills 5 five-dollar bills, 9 one-dollar bills 4 5

Solve by elimination. 6 x + 3 y = – 12 6 x + 2 y = – 4 1. 2. 3. 4. 1 (10, – 16) (2, – 8) (– 2, 8) (– 10, 16) 2 3 4 5

3 x + 3 y = – 93 x – 3 y = 21 1. 2. 3. 4. 1 (3, – 6) (– 5, 2) (3, 3) (2, – 5) 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

Which method is best for solving this system of equations? 2 x – 2 y = – 8 x + 2 y = – 1 1. 2. 3. 4. 1 2 3 4 Substitution Elimination Graphing magic 5

2 x – 2 y = – 8 x + 2 y = – 1 1. 2. 3. 4. 1 (– 14, 1) (1, 5) (– 3, 1) (0, 4) 2 3 4 5

3 x – 4 y = – 24 x + y = – 1 1. 2. 3. 4. 1 (– 4, 3) (0, 6) (3, 4) (4, 3) 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

x + 2 y = – 63 x + 8 y = – 20 1. 2. 3. 4. 1 (– 1, – 4) (– 4, – 1) (3, 1) 2 3 4 5

5 x = – 25+ 5 y 10 y = 42+ 2 x 1. 2. 3. 4. 1 (– 1, 2) (– 1, 4) (4, – 1) (5, 10) 2 3 4 5

– 10 x – 3 y = – 18 – 7 x – 8 y = 11 1. 2. 3. 4. 1 (– 7, – 10) (– 4, 3) (3, – 4) (2, – 1) 2 3 4 5

3 x – 4 y = 9 – 3 x + 2 y = 9 1. 2. 3. 4. 1 (3, 9) (– 27, – 9) (– 3, – 6) (– 9, – 9) 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

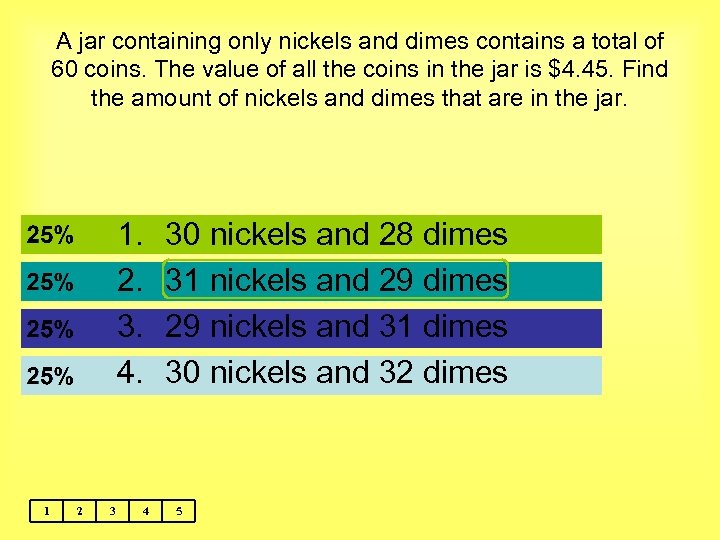A jar containing only nickels and dimes contains a total of 60 coins. The value of all the coins in the jar is $4. 45. Find the amount of nickels and dimes that are in the jar. 1. 2. 3. 4. 1 2 3 4 30 nickels and 28 dimes 31 nickels and 29 dimes 29 nickels and 31 dimes 30 nickels and 32 dimes 5

By what number should you multiply the first equation to eliminate the x ? – 3 x – 2 y = 2 – 9 x + y = 5 1. 2. 3. 4. 1 6 – 9 2 3 4 5

An ice skating arena charges an admission fee for each child plus a rental fee for each pair of ice skates. John paid the admission fees for his six nephews and rented five pairs of ice skates. He was charged $32. 00. Juanita paid the admission fees for her seven grandchildren and rented five pairs of ice skates. She was charged $35. 25. What is the admission fee? What is the rental fee for a pair of skates? 1. 2. 3. 4. 1 2 3 admission fee: $3. 25 admission fee: $3. 50 admission fee: $3. 00 admission fee: $4. 00 4 5 skate rental fee: $2. 50 skate rental fee: $3. 00 skate rental fee: $2. 00 skate rental fee: $3. 50

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

You decide to market your own custom computer software. You must invest $3, 255 for computer hardware, and spend $2. 90 to buy and package each disk. If each program sells for $13. 75, how many copies must you sell to break even? 1. 2. 3. 4. 1 196 copies 301 copies 300 copies 195 copies 2 3 4 5

Mike and Kim invest $14, 000 in equipment to print yearbooks for schools. Each yearbook costs $7 to print and sells for $35. How many yearbooks must they sell before their business breaks even? 1. 2. 3. 4. 1 650 2, 000 500 400 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5

Last question! Worth 10, 000 points … … no pressure!

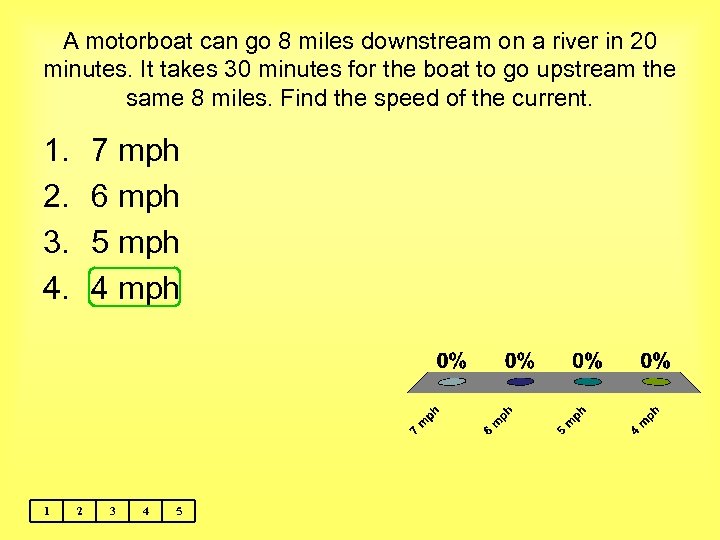A motorboat can go 8 miles downstream on a river in 20 minutes. It takes 30 minutes for the boat to go upstream the same 8 miles. Find the speed of the current. 1. 2. 3. 4. 1 7 mph 6 mph 5 mph 4 mph 2 3 4 5

Team Scores 0 0 Team 1 Team 2 Team 3 Team 4 0 Team 5