Systems Engineering for Reversible Quantum Nanocomputers Dr Mike

Systems Engineering for Reversible Quantum Nanocomputers Dr. Mike Frank University of Florida CISE Department mpf@cise. ufl. edu Presented to: University of Southern California Dept. of Electrical Engineering Wed. , May 1, 2002

Summary of Current Research • Two major projects: – The OCEAN Project (MIT 1997, UF 2000 -) • “Open Computation Exchange & Auctioning Network” – An automated, distributed P 2 P market system (w. real $) – A real-time clearinghouse for online computing resources – Works standalone, but also compatible w. existing grid systems • Developing open standards & reference implementation – Registry to be operated by an int’l non-profit organization – Reversible & Quantum Computing Project • Studying & developing physical computing theory: MIT 1970’s-1999, UF 1999 - – Technology-independent physical limits of computing – “Ultimate” models of computing for complexity theory • Nanocomputer systems engineering – Optimizing cost-efficiency scalability of future computing • Reversible computing & quantum computing – Realistic models, CPU architectures, optimal scaling advantages

The Project The Open Computation Exchange & Auctioning Network http: //www. cise. ufl. edu/research/ocean • Key long-term goals of the project: – Improve accessibility of massively-parallel distributed computing, for use in arbitrary apps. • Near-unlimited computing power, available on-demand. – Increase average level of computing resource utilization, for individuals & within organizations. • Improve the cost-efficiency of computing for everyone. – Create an open, public, dynamic, automated, online marketplace for all kinds of commodities. • Online distributed-computing resources: A special case • Democratize other commodity & financial markets?

Key Characteristics of OCEAN • Easy to install and operate node software – Like ICQ, Napster, etc. : Any teenager can do it • Easy to write and deploy distributed apps – Client API automatically negotiates purchases • Flexible, extensible resource description lang. – Based on open web-services standards: XML/SOAP – Any resources or requirements can be described – Used for advertisements, negotiation, contracts • Efficiently scalable to large numbers of nodes – Matching service is itself distributed, P 2 P-based – Centralized accounting bottleneck is minimized

OCEAN Project Status • ~10 -20 senior/MS/Ph. D students per semester • Prototype components currently under active development in Java: 1 st proto date – Communications – Task Spawning & Migration – Secure communications – Distributed auction algorithm – Adaptive P 2 P framework – Automated negotiation system – Central accounting database – Bridge to financial networks Spr. ‘ 02 Sum. ‘ 02 Fall ‘ 01 Sum. ‘ 02 Spr. ‘ 02 • Internal alpha test Fall ‘ 02, public beta Spr. ‘ 03.

Rev. Comp project heritage • Grew out of work started by the MIT Information Mechanics group in the 1970’s. – Key members: Fredkin, Toffoli, Margolus • Occasional collaboration with Feynman, Bennett, … – This group laid much of theoretical groundwork for reversible (& eventually quantum) computing. • MIT Reversible Computing group (1990 s) – Group leaders: Knight, Margolus • Students: Younis, D’Souza, Becker, Vieri, Frank, Ammer – Focus: Reducing reversible computing to practice • CMOS circuit styles, test chips, architectures, complexity theory, algorithms, high-level languages.

Rev. Comp group at UF • Reversible & Quantum Computing group – Organized by myself (CISE/ECE depts. ) – UF collabs. in CISE, ECE, Math, Phys. /Chem. – Notable graduate: Do. Ron Motter (highest honors) • Now doing Ph. D work in quantum circuits at U. Mich. – 3 current Ph. D students (all ECE) • Current focus: – Removing remaining barriers to near-term practicality of reversible computing • Improved circuit styles, efficient power supplies • Other applications – Long-term study of physical computing theory and scaling advantages of reversible/quantum models.

Nanocomputer systems engineering • A key goal of my long-term research program: – Develop the foundations for a new discipline of nanocomputer systems engineering suited for meeting the challenges of computing at the nanoscale. • And convey it to peers, teach it to students. • The new field will integrate concerns & methods from a variety of disciplines: – Physics of computing – Systems engineering – Computer architecture – Complexity theory Algorithm design Electrical eng. , etc.

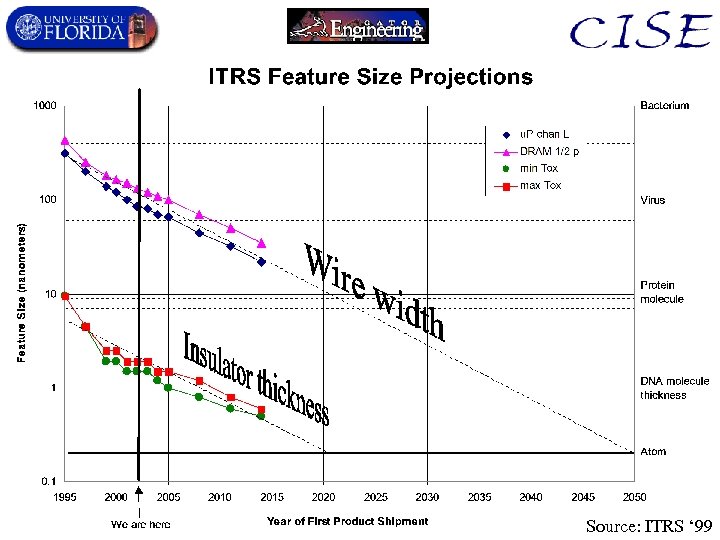
Source: ITRS ‘ 99

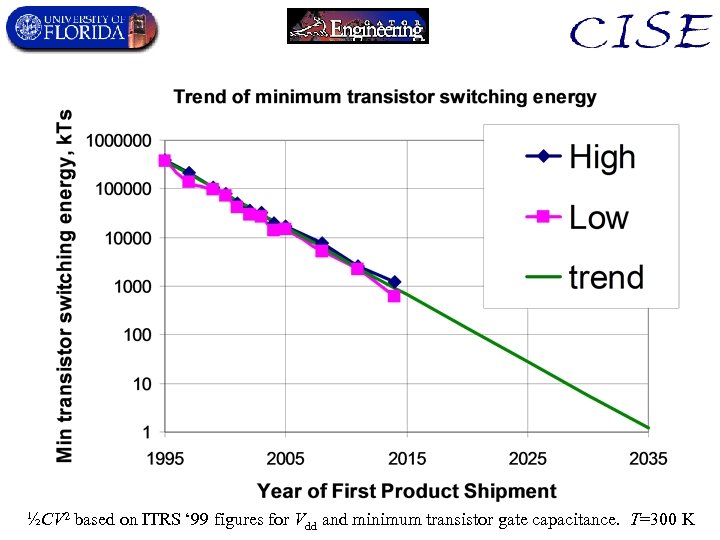
½CV 2 based on ITRS ‘ 99 figures for Vdd and minimum transistor gate capacitance. T=300 K

Physical Computing Theory • The study of theoretical models of computation that are based on (or closely tied to) physics – Make no nonphysical assumptions! • Includes the study of: – Fundamental physical limits of computing – Physically-based models of computing • Includes reversible and/or quantum models • “Ultimate” (asymptotically optimal) models – An asymptotically tight “Church’s thesis” – Model-independent basis for complexity theory • Basis for design of future nanocomputer architectures – Asymptotic scaling of architectures & algorithms • Physically optimal algorithms

Systems Engineering (my def’n) • The interdisciplinary study of the design of complex systems in which multiple areas of engineering may interact in nontrivial ways. – Optimizing a complete system will in general require considering the effect of concerns in different engineering disciplines on each other. • E. g. , simultaneous consideration of: – Mechanical (structural & dynamic) engineering – Thermal/power engineering – Electrical/electronic/photonic engineering – Algorithmic/software engineering – Economic/social/financial engineering?

Cost-Efficiency • The primary concern of systems engineering. • Cost most generally can be any appropriate measure of resources consumed. • The cost-efficiency %$ to achieve a task is the fraction $min/$ of cost $ that had to be spent. • Goal: When designing a system to accomplish a given task, choose the design that minimizes the cost $ (thus maximizes cost-efficiency). – Include design cost, amortized over expected number of reuses of the design.

Generalized Amdahl’s Law • A fundamental systems engineering principle. • Cost of a system can often be expressed as a sum $ = $1+…+$n of independent components. – Does a reduction of $i by a factor f or amt. $i have a benefit proportional to the magnitude of f or $i? • No, because: – Since there are other cost components, the factor reduction in total cost is not proportional to f. – Also, the value of the design in practice is not linear in the total cost $, but rather in cost-efficiency %$ 1/$. (Like ROI in business. ) • Leads to a law of diminishing returns.

Two-pass system optimization • A general methodology for the integrated optimization of the design of complex systems. • Performance characteristics of system expressed as a function of design parameters, & subsystem Characterize cost-efficiency characteristics. from bottom upwards • Then, optimize design parameters from top down to maximize overall system cost-efficiency. Top-level systems design High-level subsystems Mid-level components Lowest-level design elements Optimize design parameters from top downwards

Computer Systems Engineering (CSE) • General systems engineering principles applied to the design of computer systems. – E. g. : Electronic, algorithmic, thermal, and communications concerns interact when optimizing massively parallel computers for some problems • When looking ahead to the cross-disciplinary interactions that become more important for bitdevices at ~ the nanometer scale, – Call the subject “nanocomputer systems engineering” (NCSE) • This is what I do.

Ultimate Models of Computing • We would like models of computing that match the real computational power of physics. – Not too weak, not too strong. • Most traditional models of computing only match physics to within polynomial factors. – Misleading asymptotic performance of algorithms. – Not good enough to form the basis for a real systems engineering optimization of architectures. • Develop models of computing that are: – As powerful as physically possible on all problems – Realistic within asymptotic constant factors

Scalability & Maximal Scalability • A multiprocessor architecture & accompanying performance model is scalable if: – it can be “scaled up” to arbitrarily large problem sizes, and/or arbitrarily large numbers of processors, without the predictions of the performance model breaking down. • An architecture (& model) is maximally scalable for a given problem if – it is scalable and if no other scalable architecture can claim asymptotically superior performance on that problem • It is universally maximally scalable (UMS) if it is maximally scalable on all problems! – I will briefly mention some characteristics of architectures that are universally maximally scalable

Universal Maximum Scalability • Existence proof for universally maximally scalable (UMS) architectures: – Physics itself is a universal maximally scalable “architecture” because any real computer is merely a special case of a physical system. • Obviously, no real computer can beat the performance of physical systems in general. – Unfortunately, physics doesn’t give us a very simple or convenient programming model. • Comprehensive expertise at “programming physics” means mastery of all physical engineering disciplines: chemical, electrical, mechanical, optical, etc. – We’d like an easier programming model than this!

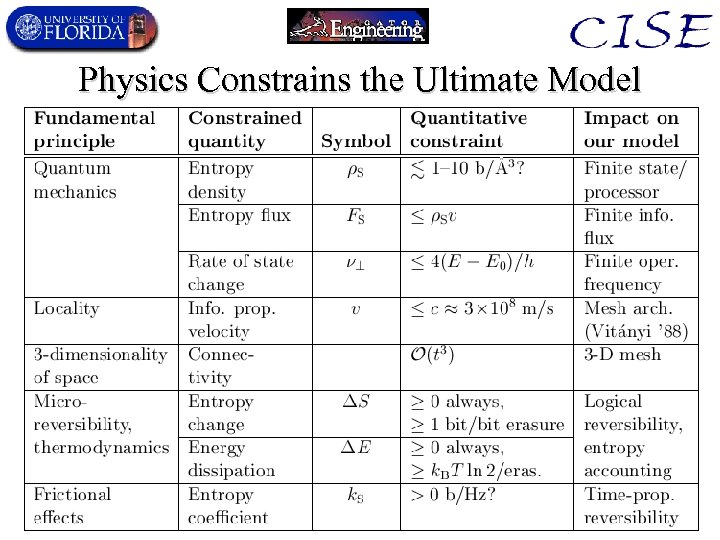
Physics Constrains the Ultimate Model

Simple UMS Architectures • (I propose) any practical UMS architecture will have the following features: – Processing elements characterized by constant parameters (independent of # of processors) – Mesh-type message-passing interconnection network, arbitrarily scalable in 2 dimensions • w. limited scalability in 3 rd dimension. – Processing elements that can be operated in a highly reversible mode, at least up to some limit. • Enables improved 3 -d scalability, in a limited regime – (In long term) Have capability for quantumcoherent operation, for extra perf. on some probs.

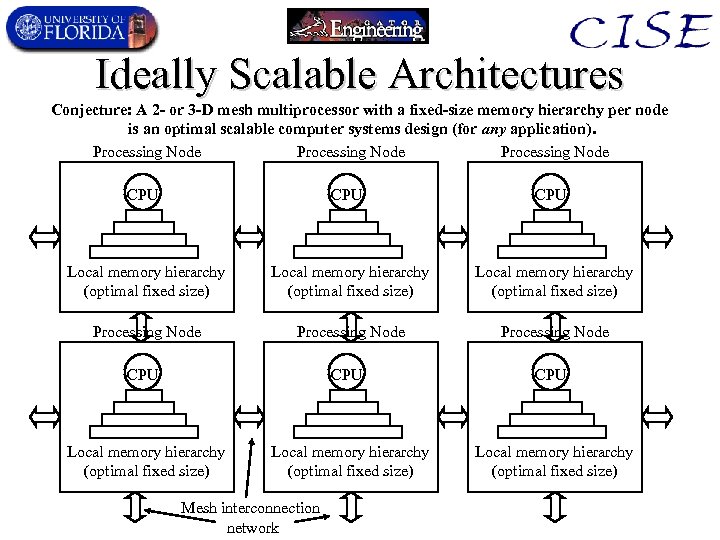
Ideally Scalable Architectures Conjecture: A 2 - or 3 -D mesh multiprocessor with a fixed-size memory hierarchy per node is an optimal scalable computer systems design (for any application). Processing Node Processing Node CPU CPU CPU Local memory hierarchy (optimal fixed size) Local memory hierarchy (optimal fixed size) Mesh interconnection network

Reversibility of Physics • The universe is (apparently) a closed system • Closed systems evolve via unitary transforms – Apparent wavefunction collapse doesn’t contradict this (confirmed by work of Everett, Zurek, etc. ) • Time-evolution of concrete state of universe (or closed subsystems) is reversible: – Invertible (bijective) – Deterministic looking backwards in time – Total info. (log # of poss. states) doesn’t decrease • Can increase, though, if volume is increasing • Information cannot be destroyed!

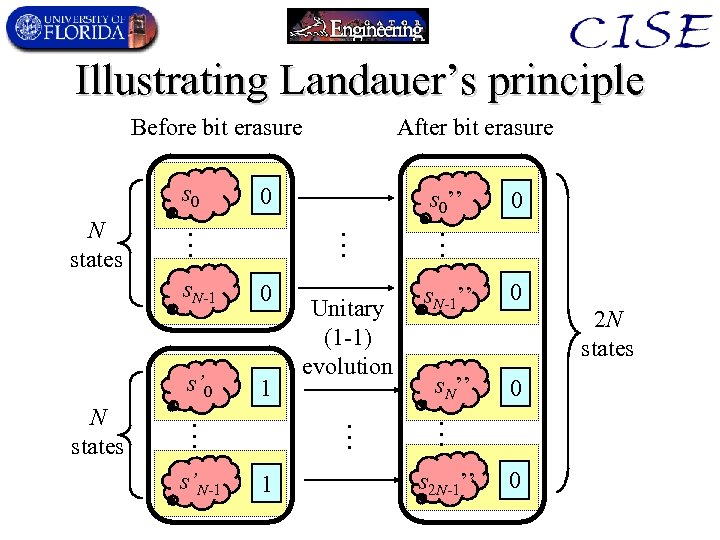
Illustrating Landauer’s principle Before bit erasure s 0 0 0 s’ 0 1 1 s. N-1’’ 0 s. N’’ 0 2 N states … … … s’N-1 Unitary (1 -1) evolution 0 … s. N-1 N states s 0’’ … … N states After bit erasure s 2 N-1’’ 0

Benefits of Reversible Computing • Reduces energy/cooling costs of computing – Improves performance per unit power consumed • Given heat flux limits in the cooling system, – Improves performance per unit convex hull area • A faster machine in a given size box. • For communication-intensive parallel algorithms, – Improves performance, period! All these benefits are by small polynomial factors in the integration scale & the device properties.

Reversible/Adiabatic CMOS • Chips designed at MIT, 1996 -1999:

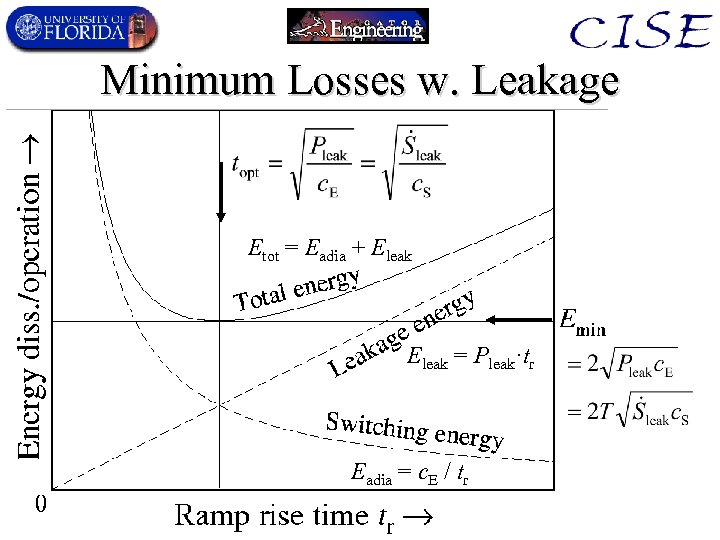
Minimum Losses w. Leakage Etot = Eadia + Eleak = Pleak·tr Eadia = c. E / tr

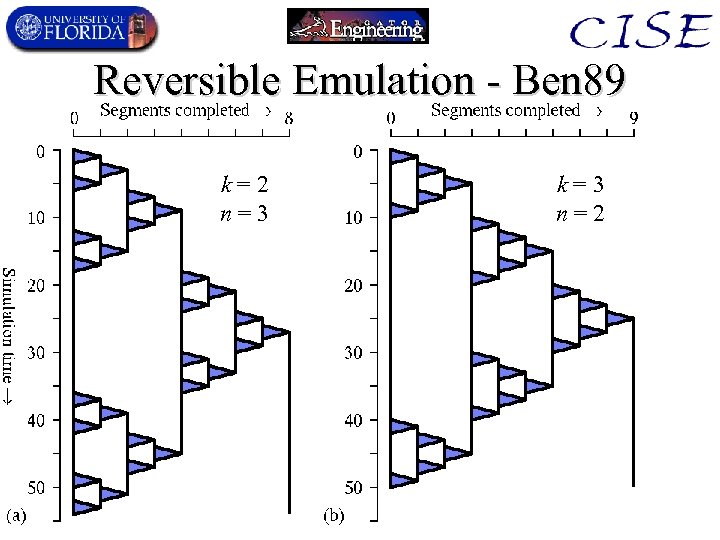
Reversible Emulation - Ben 89 k=2 n=3 k=3 n=2

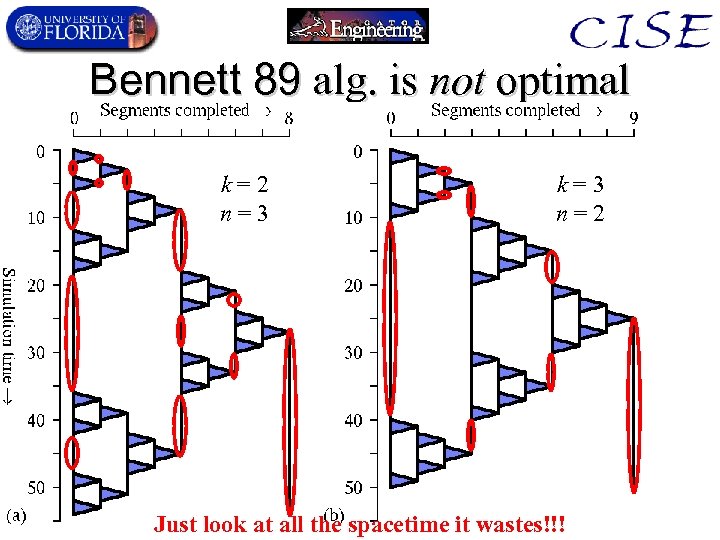
Bennett 89 alg. is not optimal k=2 n=3 k=3 n=2 Just look at all the spacetime it wastes!!!

Parallel “Frank 02” algorithm • We can move the triangles closer together, to eliminate the wasted spacetime. • Resulting algorithm is linear time for all n and k and dominates Ben 89 for time, spacetime, & energy! Emulated time k=2 n=3 k=3 n=2 k=4 n=1 Real time

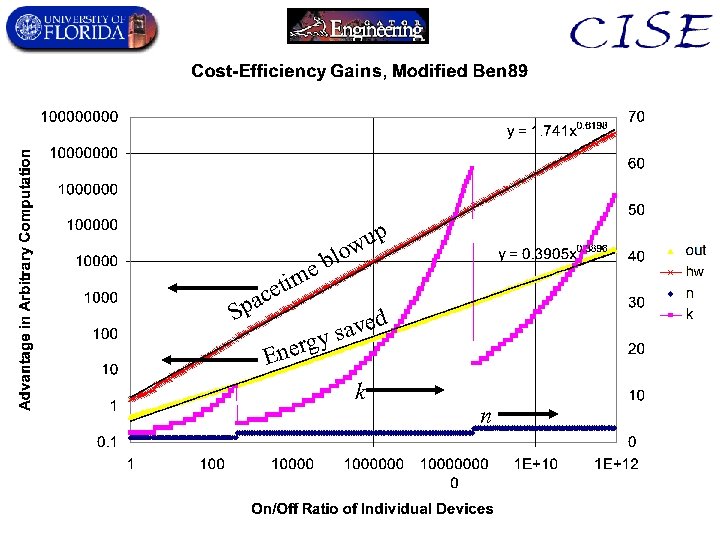
p eb etim pac S wu lo aved ys nerg E k n

Perf. scaling w. # of devices • If alg. is not limited by communications needs, – Use irreversible processors spread in a 2 -D layer. – Remove entropy along perpendicular dimension. – No entropy rate limits, • so no speed advantage from reversibility. • If alg. requires only local communication, latency cyc. time, in an ND×ND×ND mesh, – Leak-free reversible machine perf. scales better! – Irreversible tcyc = (ND 1/3) – Reversible tcyc = (ND 1/4)… (ND 1/12) × faster! • To boost reversibility speedup by 10×, one must consider ~1036 -CPU machines (1. 7 trillion moles of CPUs!) – 1. 7 trillion moles of H atoms weighs 1. 7 million metric tons! » A ~100 -m tall hill of H-atom sized CPUs!

Lower bound on irrev. time • • • Simulate Nproc = ND 3 cells for Nsteps » ND steps. Consider a sequence of ND update steps. Final cell value depends on ND 4 ops in time T. All ops must occur within radius r = c. T of cell. Surface area A T 2, rate Rop T 2 sustainable. Nops Rop T T 3 needs to be at least ND 4. T must be (ND 4/3) to do all ND steps. Average time per step must be (ND 1/3). Any irreversible machine (of any technology or architecture) must obey this bound!

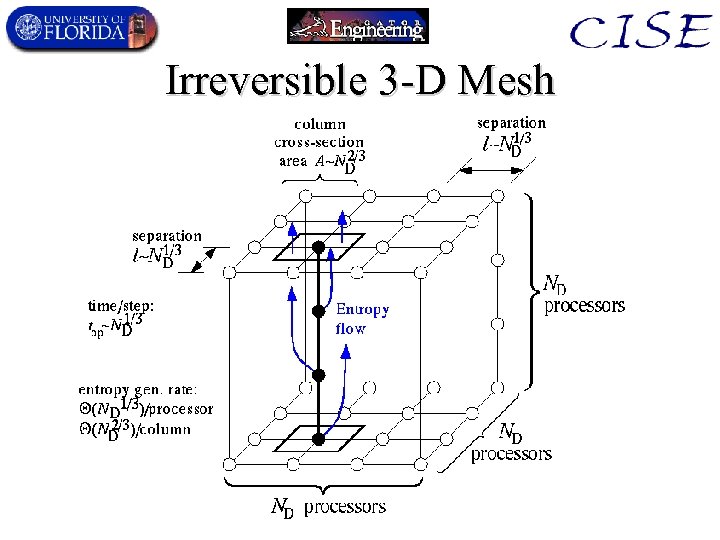
Irreversible 3 -D Mesh

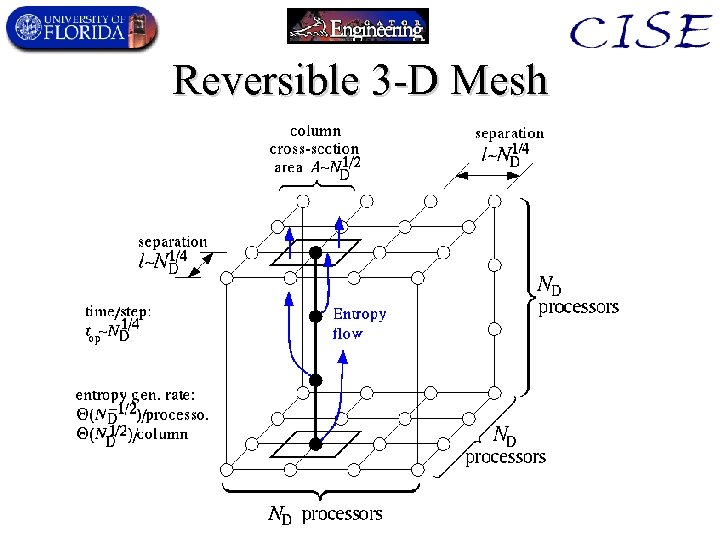
Reversible 3 -D Mesh

Non-local Communication • Best computational task for reversibility: – Each processor must exchange messages with another that is ND 1/2 nodes away on each cycle • Unsure what real-world problem demands this pattern! – In this case, reversible speedup scales with number of CPUs to “only” the 1/18 th power. • To boost reversibility speedup by 10×, “only” need 1018 (or 1. 7 micromoles) of CPUs • If each was a 1 -nm cluster of 100 C atoms, this is only 2 mg mass, volume 1 mm 3. • Current VLSI: Need cost level of ~$25 B before you see a speedup.

Open issues for reversible comp. • Integrate realistic fundamental models of the clocking system into the engineering analysis. – There is an open issue about the scalability of clock distribution systems. • Exist quantum bounds on reusability of timing signals. • Not yet clear if reversible clocking is scalable. – Fortunately, self-timed reversible computing also appears to be a possibility. • Not yet clear if this approach works above 1 -D models. • Simulation experiments planned to investigate this. • Develop efficient physical realizations of nanoscale bit-devices & timing systems.

Quantum Computing pros/cons • Pros: – Removes an unnecessary restriction on the types of quantum states & ops usable for computation. – Opens up exponentially shorter paths to solving some types of problems (e. g. , factoring, simulation) • Cons: – Sensitive, requires overhead for error correction. – Also, still remains subject to fundamental physical bounds on info. density, & rate of state change! • Myth: “A quantum memory can store an exponentially large amount of data. ” • Myth: “A quantum computer can perform operations at an exponentially faster rate than a classical one. ”

Some goals of my QC work • Develop a UMS model of computation that incorporates quantum computing. • Design & simulate quantum computer architectures, programming languages, etc. • Describe how to do the systems-engineering optimization of quantum computers for various problems of interest.

Conclusion • As we near the physical limits of computing, – Further improvements will require an increasingly sophisticated interdisciplinary integration of concerns across many levels of engineering. • I am developing a principled nanocomputer systems engineering methodology – And applying it to the problem of determining the real cost-efficiency of new models of computing: • Reversible computing • Quantum computing • Building the foundations of a new discipline that will be critical in coming decades.