System Modeling and Formal Verification with UCLID Randal

System Modeling and Formal Verification with UCLID Randal E. Bryant Carnegie Mellon University http: //www. cs. cmu. edu/~bryant

Applying Data Abstraction to Hardware Verification Idea n Abstract details of data encodings and operations n Keep control logic precise Applications n n Verify overall correctness of system Assuming individual functional units correct Technology n n n – 2– Use restricted subset of first-order logic Implement efficient decision procedures Multiple methods of performing verification

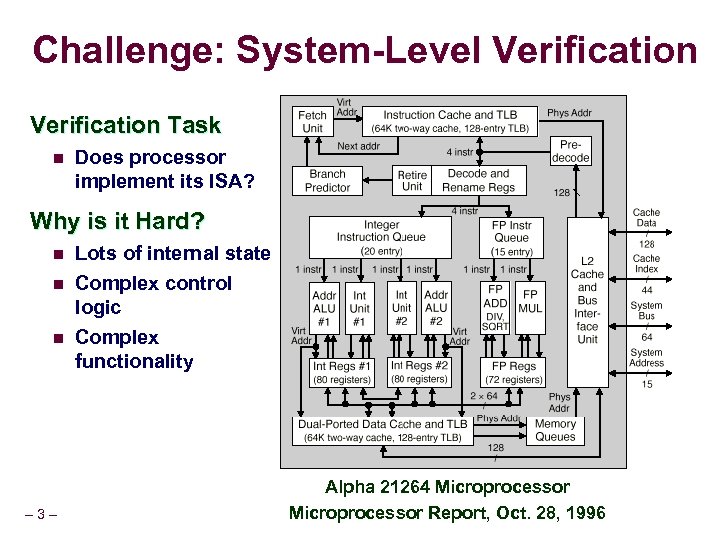Challenge: System-Level Verification Task n Does processor implement its ISA? Why is it Hard? n n n – 3– Lots of internal state Complex control logic Complex functionality Alpha 21264 Microprocessor Report, Oct. 28, 1996

Existing Verification Methods n Simulators, equivalence checkers, model checkers, … All Operate at Bit Level n RTL model l State encoded as words and arrays of words l Comprised of bits Most Operate at Cycle or Subcycle Level n How each bit of state gets updated System Modeling Languages n n – 4– Abstract time up to transaction level Still view state as collection of bits

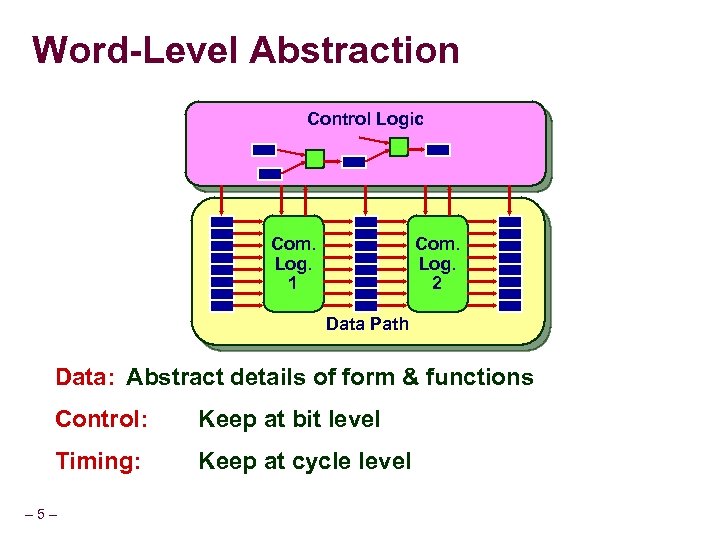Word-Level Abstraction Control Logic Com. Log. 1 Com. Log. 2 Data Path Data: Abstract details of form & functions Control: Keep at bit level Timing: Keep at cycle level – 5–

Data Abstraction #1: Bits → Integers x 0 x 1 x 2 xn-1 View Data as Symbolic Words n Arbitrary integers l No assumptions about size or encoding l Classic model for reasoning about software n – 6– Can store in memories & registers x

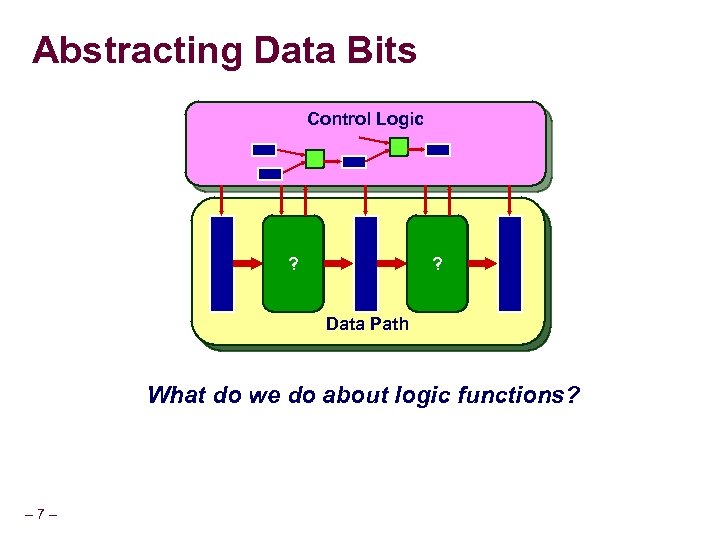Abstracting Data Bits Control Logic Com. ? Log. 1 2 Data Path What do we do about logic functions? – 7–

Abstraction #2: Uninterpreted Functions ALU f For any Block that Transforms or Evaluates Data: n Replace with generic, unspecified function n Only assumed property is functional consistency: a = x b = y f (a, b) = f (x, y) – 8–

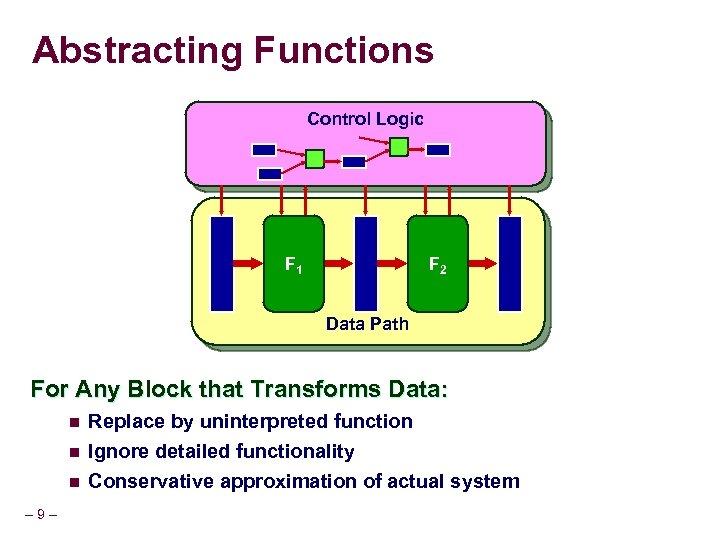Abstracting Functions Control Logic Com. F 1 Log. 1 Com. F 2 Log. 1 Data Path For Any Block that Transforms Data: n Replace by uninterpreted function n Ignore detailed functionality Conservative approximation of actual system n – 9–

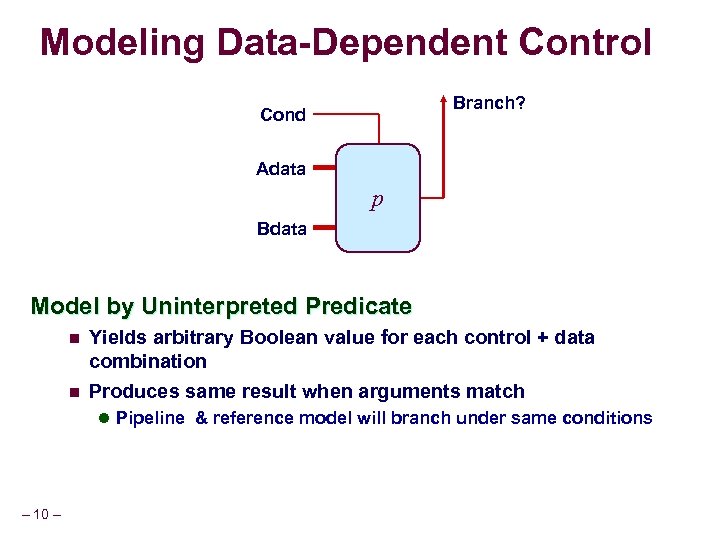Modeling Data-Dependent Control Branch? Adata Branch Logic Cond p Bdata Model by Uninterpreted Predicate n n Yields arbitrary Boolean value for each control + data combination Produces same result when arguments match l Pipeline & reference model will branch under same conditions – 10 –

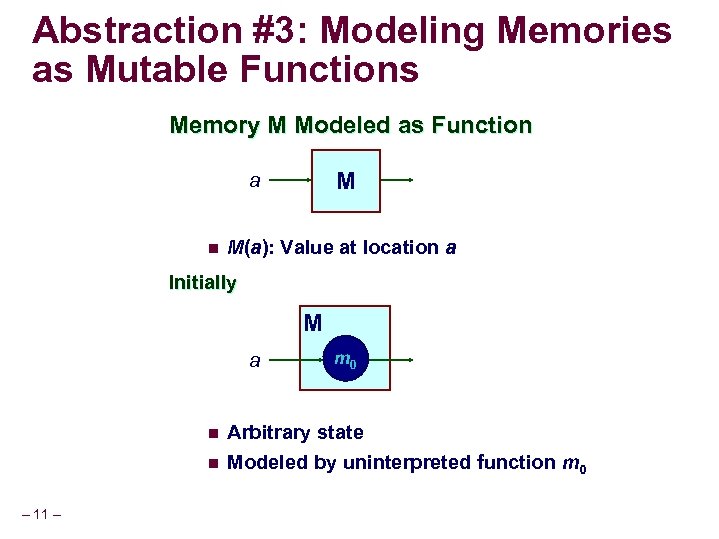Abstraction #3: Modeling Memories as Mutable Functions Memory M Modeled as Function M a n M(a): Value at location a Initially M a n n – 11 – m 0 Arbitrary state Modeled by uninterpreted function m 0

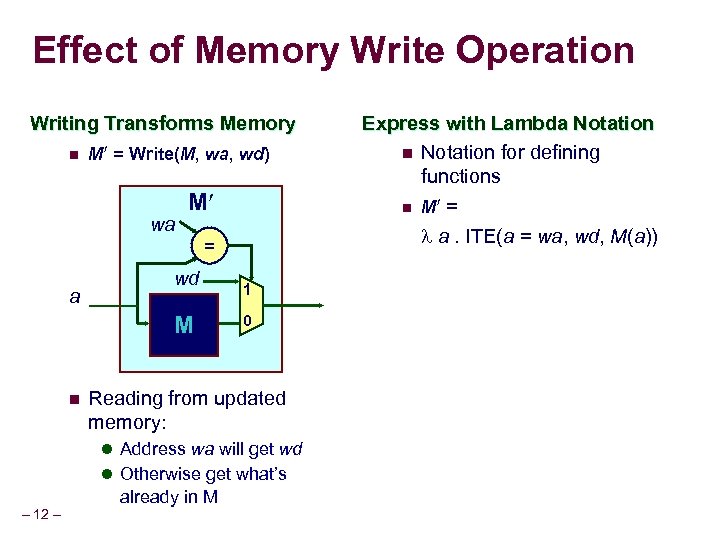Effect of Memory Write Operation Writing Transforms Memory n M = Write(M, wa, wd) wa M = a wd M n 1 0 Reading from updated memory: l Address wa will get wd l Otherwise get what’s – 12 – already in M Express with Lambda Notation n Notation for defining functions n M = a. ITE(a = wa, wd, M(a))

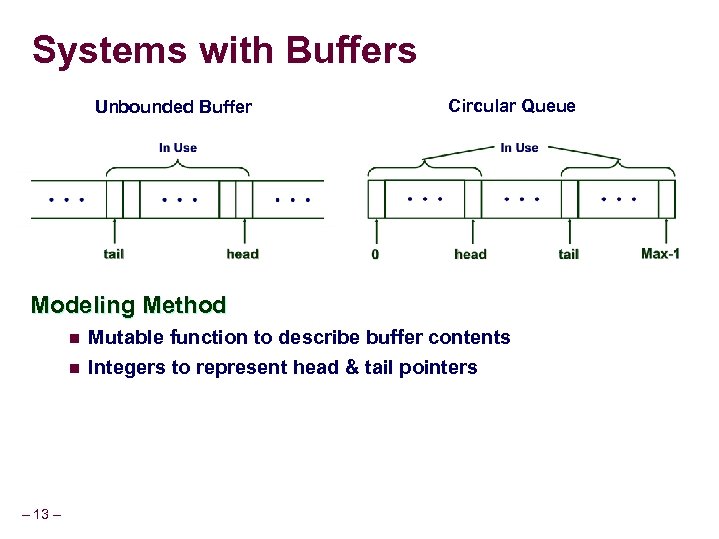Systems with Buffers Unbounded Buffer Circular Queue Modeling Method n n – 13 – Mutable function to describe buffer contents Integers to represent head & tail pointers

Some History of Term-Level Modeling Historically n Standard model used for program verification n Widely used with theorem-proving approaches to hardware verification l E. g, Hunt ’ 85 Automated Approaches to Hardware Verification n Burch & Dill, ’ 95 l Tool for verifying pipelined microprocessors l Implemented by form of symbolic simulation n Continued application to pipelined processor verification Real World Applications n – 14 – Recently used by Intel for microcode verification (CAV 2005)

UCLID n Seshia, Lahiri, Bryant, CAV ‘ 02 Term-Level Verification System n Language for describing systems l Inspired by CMU SMV n Symbolic simulator l Generates integer expressions describing system state after sequence of steps n Decision procedure l Determines validity of formulas n Support for multiple verification techniques Available by Download http: //www. cs. cmu. edu/~uclid – 15 –

Challenge: Model Generation n n How to generate term-level model How to guarantee faithfulness to RTL description Comparison of Models n RTL l Abstracts functional elements from gate-level model l Synthesis allows automatic map to gate level n Term level l Abstracts bit-level data representations to words l Abstracts memories to mutable functions l No direct connection to synthesizable model – 16 –

Generating Term-Level Model Manually Generate from RTL n How do we know it is a valid abstraction? n Hard to keep consistent with changing RTL Automatically Generate from RTL n n Andraus & Sakallah, DAC ‘ 04 Must decide which signals to keep Boolean, which to abstract l Confused by bit field extraction primitives of HDL – 17 –

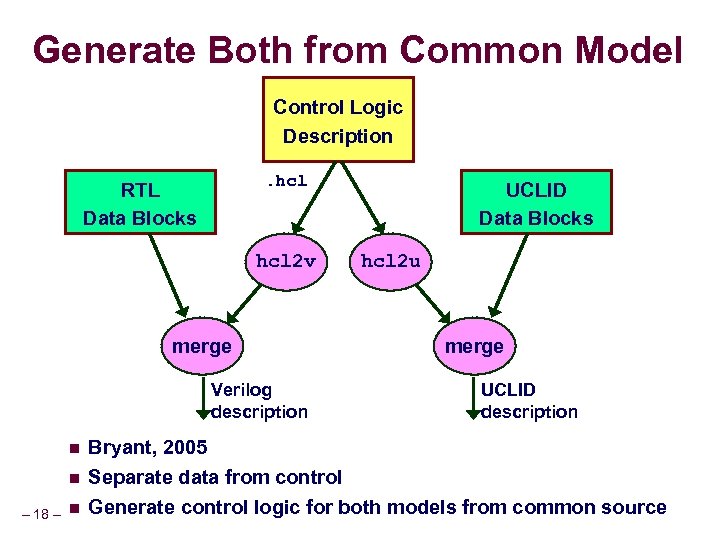Generate Both from Common Model Control Logic Description. hcl RTL Data Blocks hcl 2 v merge Verilog description n n – 18 – n UCLID Data Blocks hcl 2 u merge UCLID description Bryant, 2005 Separate data from control Generate control logic for both models from common source

Underlying Logic Existing Approaches to Formal Verification n E. g. , symbolic model checking n State encoded as fixed set of bits l Finite state system l Amenable to Boolean methods (SAT, BDDs) Our Task n State encoded with unbounded data types l Arbitrary integers l Functions over integers n Must use decision procedures l Determine validity of formula in some subset of first-order logic l Adapt methods historically used by automated theorem provers – 19 –

EUF: Equality with Uninterp. Functs n Decidable fragment of first order logic Formulas (F ) Boolean Expressions F, F 1 F 2 Boolean connectives T 1 = T 2 Equation P (T 1, …, Tk) Predicate application Terms (T ) Integer Expressions ITE(F, T 1, T 2) If-then-else Fun (T 1, …, Tk) Function application Functions (Fun) Integer f Uninterpreted function symbol x 1, …, xk. T Function lambda expression Predicates (P) p – 20 – Integer Boolean Uninterpreted predicate symbol

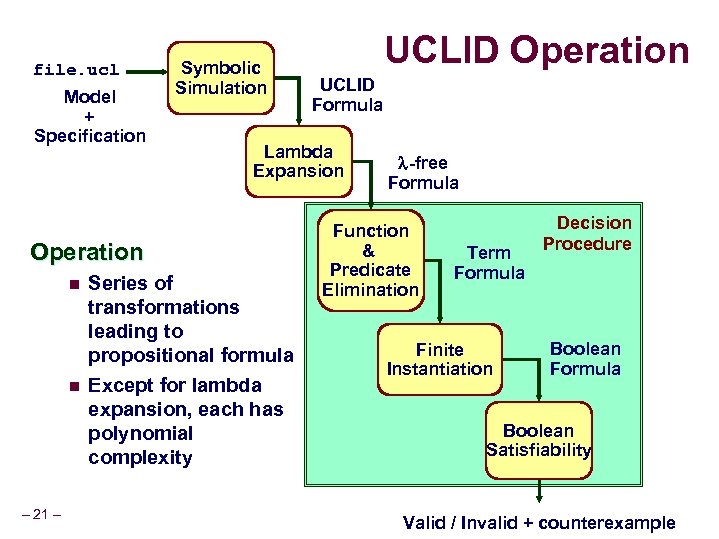file. ucl Model + Specification Symbolic Simulation n – 21 – UCLID Formula Lambda Expansion Operation n UCLID Operation Series of transformations leading to propositional formula Except for lambda expansion, each has polynomial complexity -free Formula Function & Predicate Elimination Term Formula Finite Instantiation Decision Procedure Boolean Formula Boolean Satisfiability Valid / Invalid + counterexample

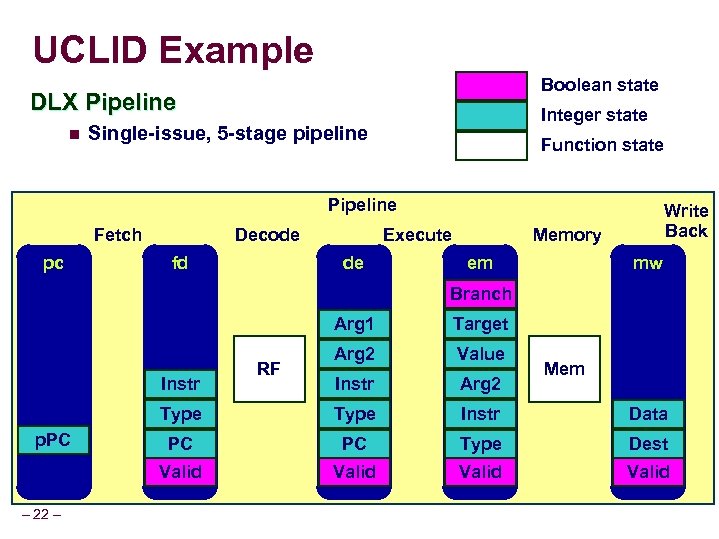UCLID Example Boolean state DLX Pipeline n Integer state Single-issue, 5 -stage pipeline Function state Pipeline Fetch pc Decode fd Execute de Write Back Memory mw em Branch Arg 1 Target Arg 2 Value Instr Arg 2 Type Instr Data PC PC Type Dest Valid Instr p. PC – 22 – RF Mem

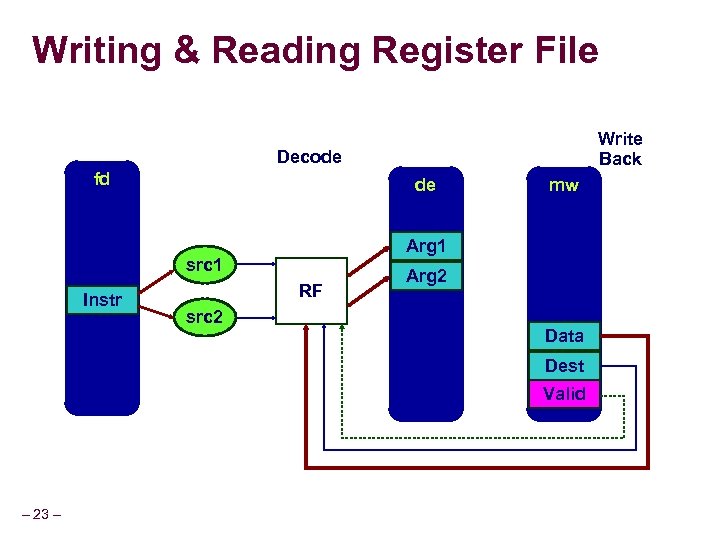Writing & Reading Register File Write Back Decode fd de Arg 1 src 1 Instr RF src 2 mw Arg 2 Data Dest Valid – 23 –

Writing Register File init[RF] : = rf 0; (* Uninterpreted Function *) next[RF] : = Lambda(a). Write case Back mw_Valid & (a = mw_Dest) : mw_Data; mw default : RF(a); esac; RF Data Dest Valid – 24 –

Reading Register File init[de_Arg 1] : = dea 10; (* Initially arbitary *) next[de_Arg 1] : = next[RF](src 1(fd_Instr)); init[de_Arg 2] : = dea 20; (* Initially arbitary *) next[de_Arg 2] : = next[RF](src 2(fd_Instr)); Decode fd de Write-before-read semantics Arg 1 src 1 Instr – 25 – RF src 2 Arg 2

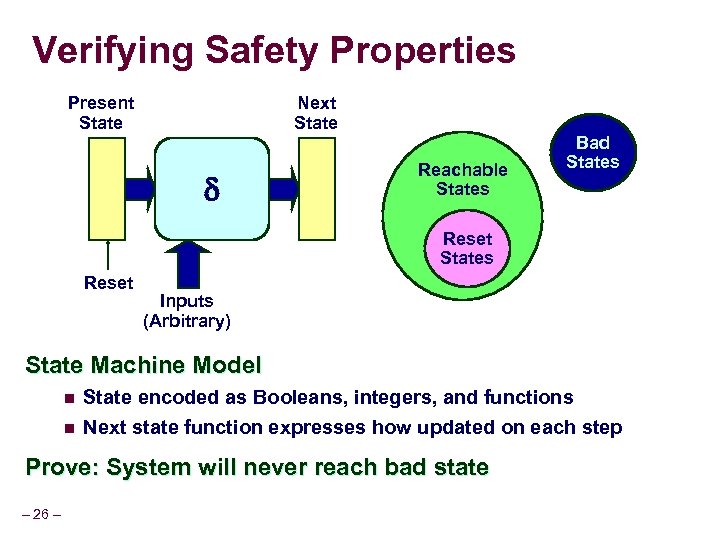Verifying Safety Properties Present State Next State Reachable States Bad States Reset Inputs (Arbitrary) State Machine Model n State encoded as Booleans, integers, and functions n Next state function expresses how updated on each step Prove: System will never reach bad state – 26 –

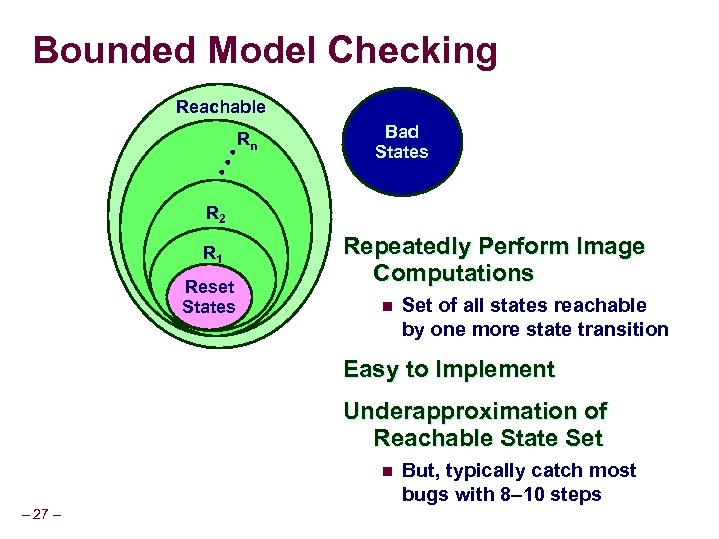Bounded Model Checking Reachable Bad States • • • Rn R 2 R 1 Reset States Repeatedly Perform Image Computations n Set of all states reachable by one more state transition Easy to Implement Underapproximation of Reachable State Set n – 27 – But, typically catch most bugs with 8– 10 steps

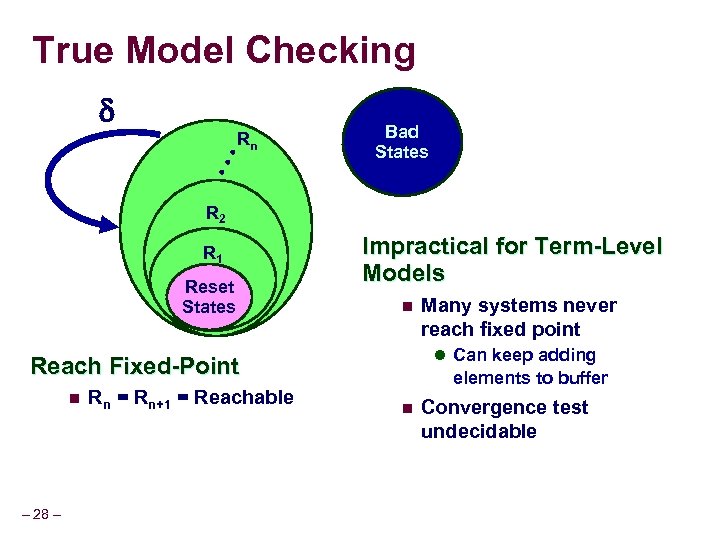True Model Checking Bad States • • • Rn R 2 R 1 Reset States Impractical for Term-Level Models n l Can keep adding Reach Fixed-Point n – 28 – Rn = Rn+1 = Reachable Many systems never reach fixed point elements to buffer n Convergence test undecidable

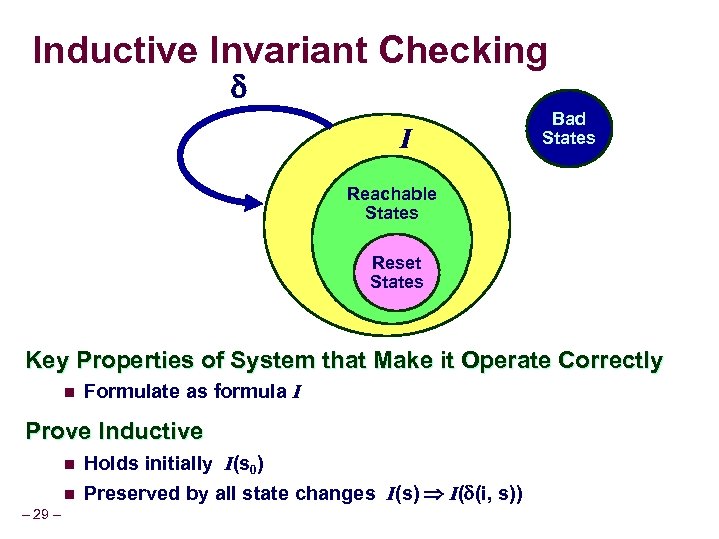Inductive Invariant Checking I Bad States Reachable States Reset States Key Properties of System that Make it Operate Correctly n Formulate as formula I Prove Inductive n n – 29 – Holds initially I(s 0) Preserved by all state changes I(s) I( (i, s))

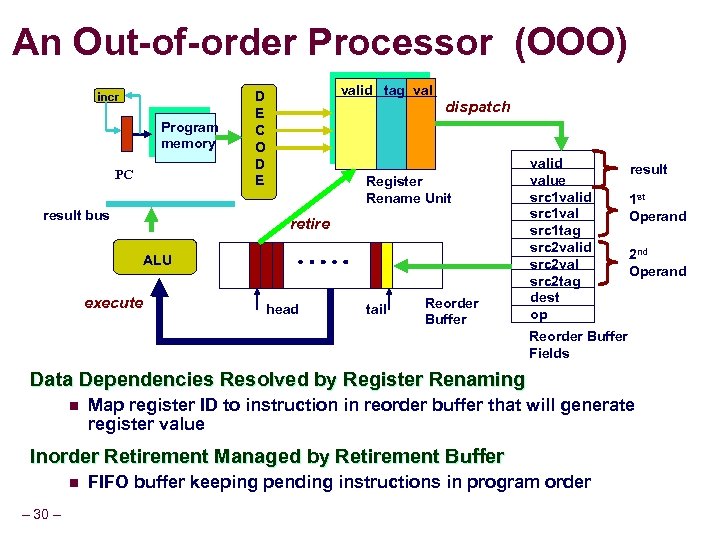An Out-of-order Processor (OOO) incr Program memory PC result bus valid tag val D E C O D E dispatch Register Rename Unit retire ALU execute head tail Reorder Buffer valid value src 1 valid src 1 val src 1 tag src 2 valid src 2 val src 2 tag dest op result 1 st Operand 2 nd Operand Reorder Buffer Fields Data Dependencies Resolved by Register Renaming n Map register ID to instruction in reorder buffer that will generate register value Inorder Retirement Managed by Retirement Buffer n – 30 – FIFO buffer keeping pending instructions in program order

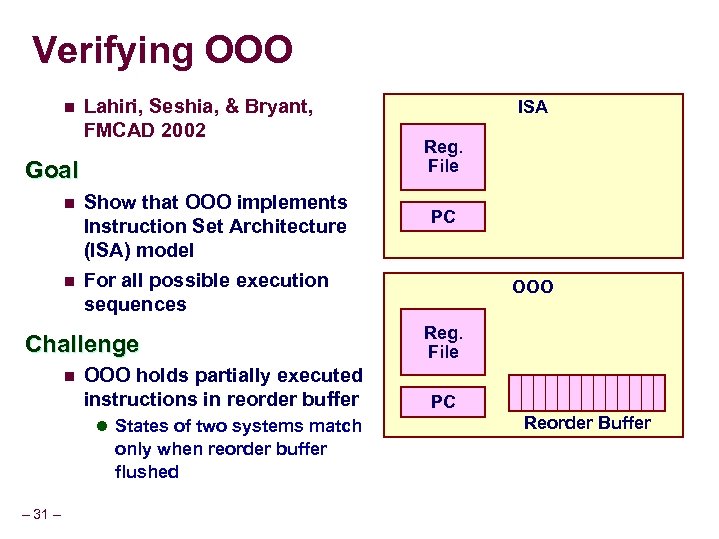Verifying OOO n Lahiri, Seshia, & Bryant, FMCAD 2002 Goal n n Show that OOO implements Instruction Set Architecture (ISA) model For all possible execution sequences Challenge n OOO holds partially executed instructions in reorder buffer l States of two systems match only when reorder buffer flushed – 31 – ISA Reg. File PC OOO Reg. File PC Reorder Buffer

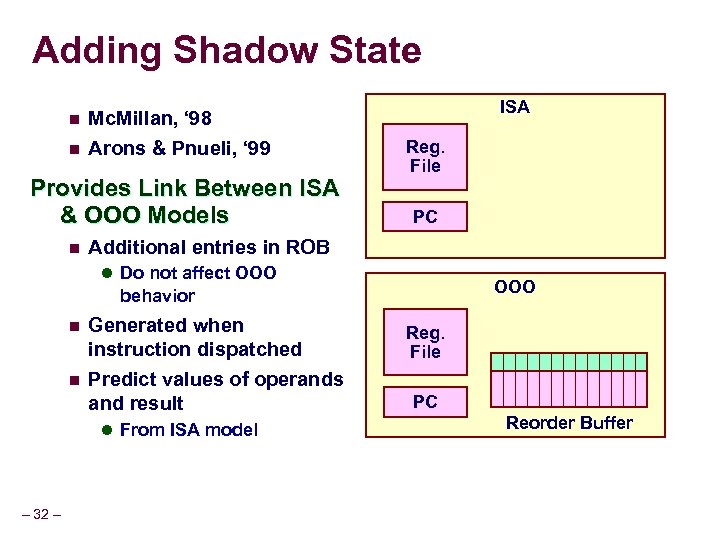Adding Shadow State n n Mc. Millan, ‘ 98 Arons & Pnueli, ‘ 99 Provides Link Between ISA & OOO Models n ISA Reg. File PC Additional entries in ROB l Do not affect OOO behavior n n Generated when instruction dispatched Predict values of operands and result l From ISA model – 32 – Reg. File PC Reorder Buffer

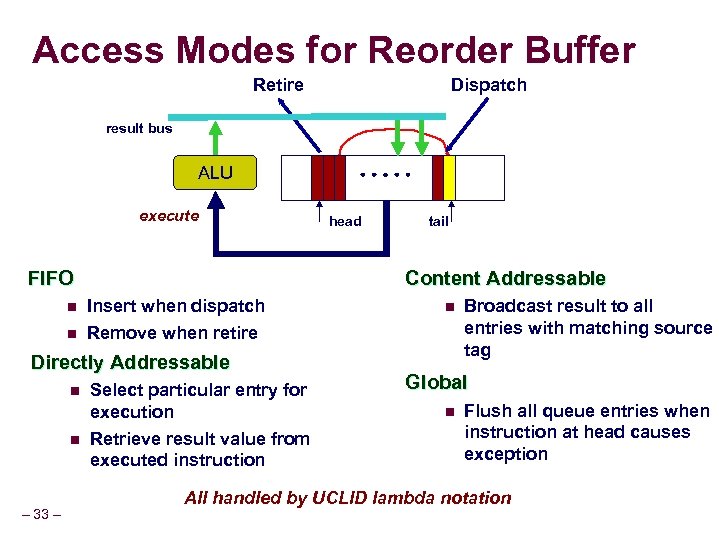Access Modes for Reorder Buffer Retire Dispatch result bus ALU execute FIFO n n n – 33 – tail Content Addressable Insert when dispatch Remove when retire Directly Addressable n head Select particular entry for execution Retrieve result value from executed instruction n Broadcast result to all entries with matching source tag Global n Flush all queue entries when instruction at head causes exception All handled by UCLID lambda notation

OOO Invariants Split into Formulas I 1, …, In n Ij(s 0) holds for any initial state s 0, for 1 j n I 2(s) … In(s) Ij(s ) for any current state s and successor state s for 1 j n n I 1(s) Invariants for OOO (13) n Refinement maps (2) l Show relation between ISA and OOO models n State consistency (8) l Properties of OOO state that ensure properation n Added state (3) l Shadow values correctly predict OOO values Overall Correctness n – 34 – Follows by induction on time

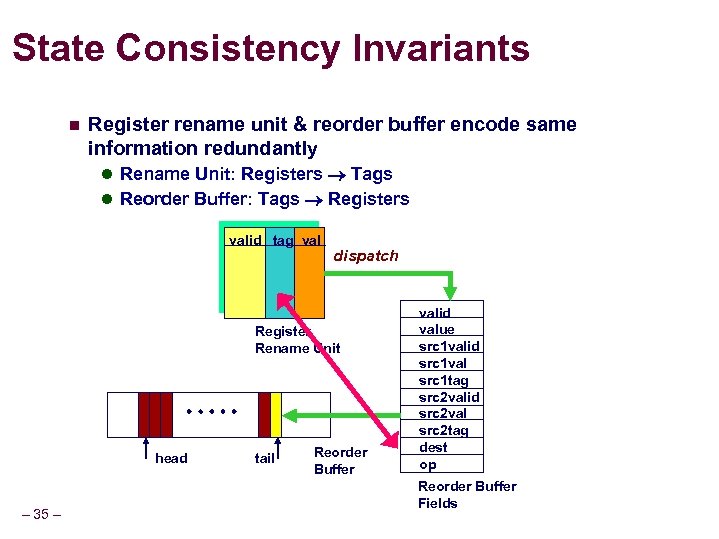State Consistency Invariants n Register rename unit & reorder buffer encode same information redundantly l Rename Unit: Registers Tags l Reorder Buffer: Tags Registers valid tag val dispatch Register Rename Unit head – 35 – tail Reorder Buffer valid value src 1 valid src 1 val src 1 tag src 2 valid src 2 val src 2 tag dest op Reorder Buffer Fields

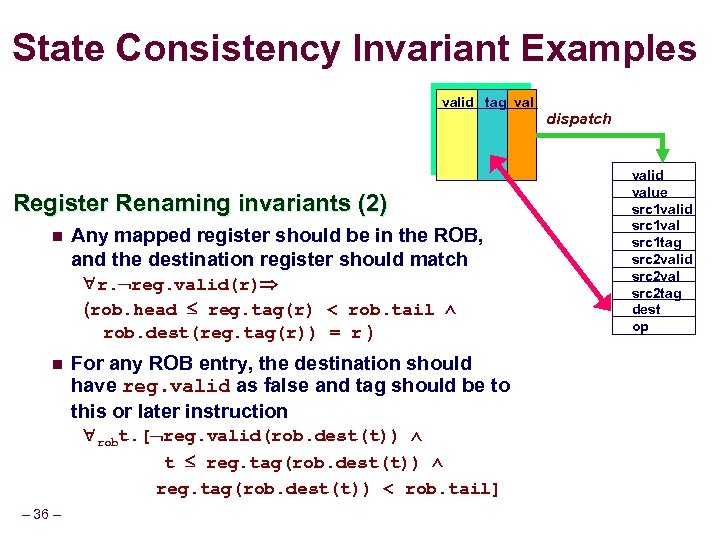State Consistency Invariant Examples valid tag val Register Renaming invariants (2) n Any mapped register should be in the ROB, and the destination register should match r. reg. valid(r) (rob. head reg. tag(r) < rob. tail rob. dest(reg. tag(r)) = r ) n For any ROB entry, the destination should have reg. valid as false and tag should be to this or later instruction robt. [ reg. valid(rob. dest(t)) t reg. tag(rob. dest(t)) < rob. tail] – 36 – dispatch valid value src 1 valid src 1 val src 1 tag src 2 valid src 2 val src 2 tag dest op

Extending the OOO Processor n base l Executes ALU instructions only n exc l Handles arithmetic exceptions l Must flush reorder buffer n exc/br l Handles branches l Predicts branch & speculatively executes along path n exc/br/mem-simp l Adds load & store instructions l Store commits as instruction retires n exc/br/mem l Stores held in buffer l Can commit later – 37 – l Loads must scan buffer for matching addresses

Comparative Verification Effort Decision Procedures n UCLID: Complete reduction to SAT n Barcelona DPLL(T): Iterative refinement to SAT base Total Invariants UCLID time DPLL(T) time Person time – 38 – exc / br / mem-simp mem 39 67 71 13 34 54 s 236 s 403 s 1 s 4 s 7 s 2 days 7 days 9 days 1594 s 2200 s 85 s 24 days 34 days

“I Just Want a Loaf of Bread” Ingredients Recipe – 39 – Result

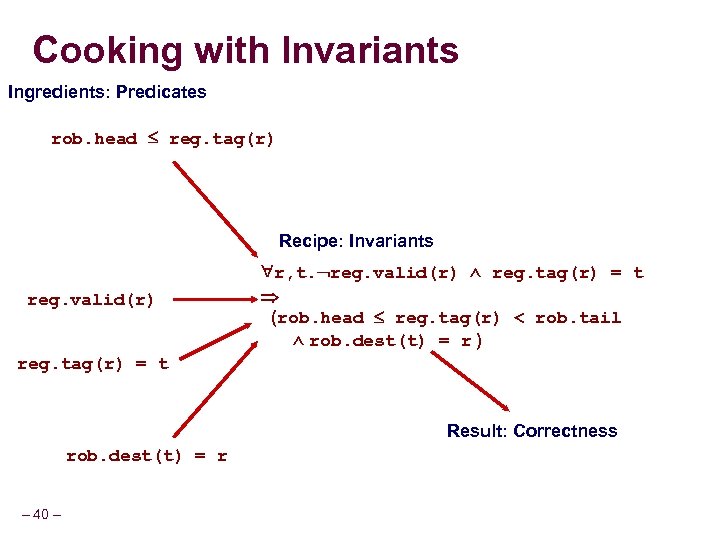Cooking with Invariants Ingredients: Predicates rob. head reg. tag(r) Recipe: Invariants reg. valid(r) r, t. reg. valid(r) reg. tag(r) = t (rob. head reg. tag(r) < rob. tail rob. dest(t) = r ) reg. tag(r) = t Result: Correctness rob. dest(t) = r – 40 –

Automatic Recipe Generation Ingredients Recipe Creator Result Want Something More n n – 41 – Given any set of ingredients Generate best recipe possible

Automatic Predicate Abstraction n Graf & Saïdi, CAV ‘ 97 Idea n Given set of predicates P 1(s), …, Pk(s) l Boolean formulas describing properties of system state n n View as abstraction mapping: States {0, 1}k Defines abstract FSM over state set {0, 1}k l Form of abstract interpretation l Do reachability analysis similar to symbolic model checking Implementation n Early ones had weak inference capabilities l Call theorem prover or decision procedure to test each potential transition n – 42 – Recent ones make better use of symbolic encodings

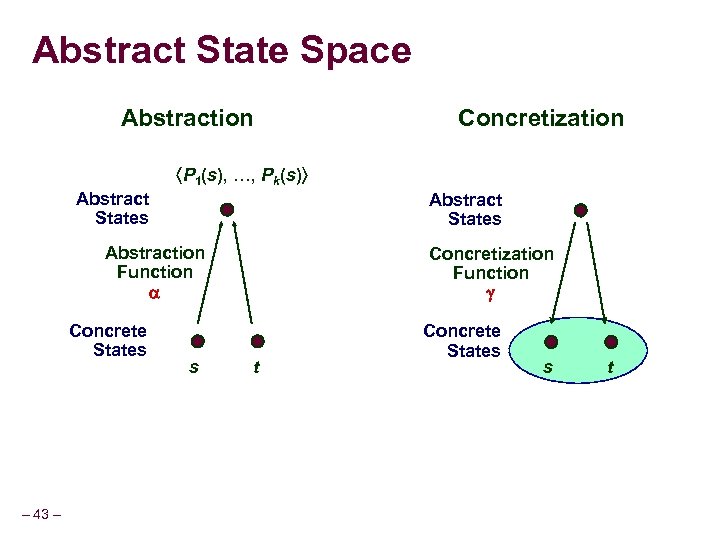Abstract State Space Abstraction Concretization P 1(s), …, Pk(s) Abstract States Abstraction Function Concrete States – 43 – s Concretization Function t Concrete States s t

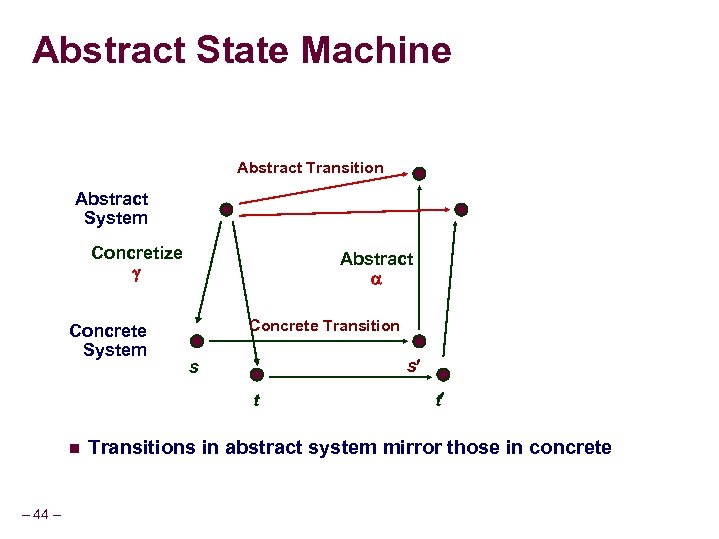Abstract State Machine Abstract Transition Abstract System Concretize Concrete System Abstract Concrete Transition s s t n – 44 – t Transitions in abstract system mirror those in concrete

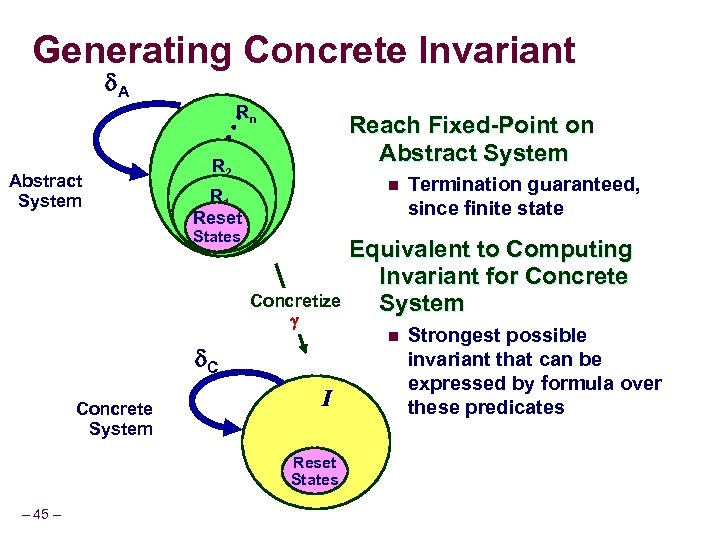Generating Concrete Invariant A Rn • • • Reach Fixed-Point on Abstract System R 2 n R 1 Reset States Concretize C Concrete System I Reset States – 45 – Termination guaranteed, since finite state Equivalent to Computing Invariant for Concrete System n Strongest possible invariant that can be expressed by formula over these predicates

Quantified Invariant Generation (Lahiri & Bryant, VMCAI 2004) n User supplies predicates containing free variables n Generate globally quantified invariant Example n Predicates p 1: reg. valid(r) p 2: reg. tag(r) = t p 3: rob. dest(t) = r n Abstract state satisfying ( p 1 p 2 p 3) corresponds to concrete state satisfying r, t[ reg. valid(r) reg. tag(r) = t rob. dest(t) = r] rather than r[ reg. valid(r)] r, t[reg. tag(r) = t] r, t[rob. dest(t) = r] – 46 –

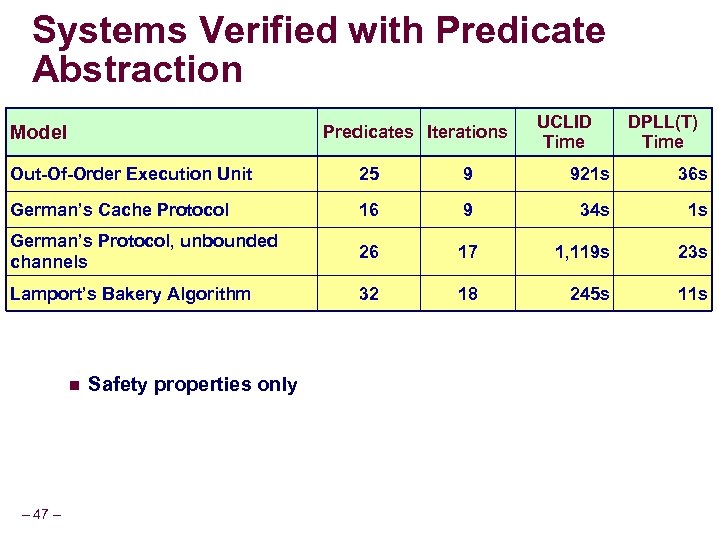Systems Verified with Predicate Abstraction Model Predicates Iterations UCLID Time DPLL(T) Time Out-Of-Order Execution Unit 25 9 921 s 36 s German’s Cache Protocol 16 9 34 s 1 s German’s Protocol, unbounded channels 26 17 1, 119 s 23 s Lamport’s Bakery Algorithm 32 18 245 s 11 s n – 47 – Safety properties only

Automatic Predicate Discovery Strength of Predicate Abstraction n If give it right set of predicates, PA will put them together into invariant Weakness n n Gets nowhere without right set of predicates Typical failure mode: Generate “true” as invariant Challenges n n – 48 – Too many predicates will overwhelm PA engine Our use of quantified invariants precludes counterexamplegenerated refinement techniques

Implementation of Predicate Discovery Lahiri & Bryant, CAV ’ 04 n Initially: Extract predicates from verification condition n Iterate: Add new predicates by composing next-state formulas l With some heuristics thrown in Experience n n – 49 – Can automatically generate invariants for real examples ~10 X slower than for hand-selected predicates

Future Prospects Evaluation n n Important to abstract data & data functions while maintaining details about control Demonstrated ability to verify complex, parameterized systems Model Generation is Weakest Link n Big jump from bit-level to term-level l Look at intermediate levels of abstraction with bit-vectors n Need algorithmic connection between our model and RTL Predicate Abstraction Shows Promise n – 50 – Provides key automation advantage of model checking