Synthesizing High-Frequency Rules from Different Data Sources Xindong

Synthesizing High-Frequency Rules from Different Data Sources Xindong Wu and Shichao Zhang IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 15, NO. 2, MARCH/APRIL 2003 1

Pre-work Knowledge management. Knowledge discovery Data mining. Data warehouse 2

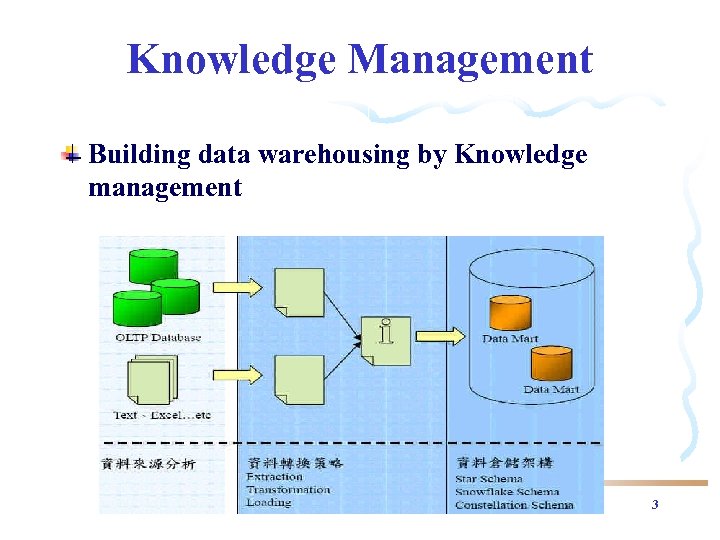Knowledge Management Building data warehousing by Knowledge management 3

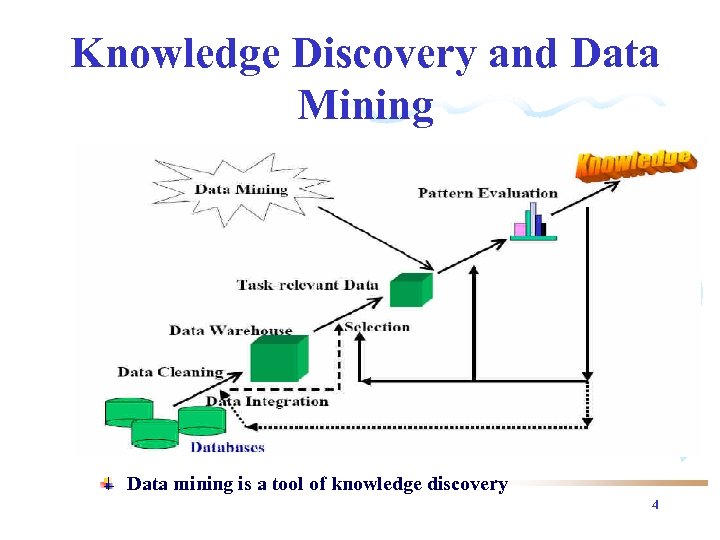Knowledge Discovery and Data Mining Data mining is a tool of knowledge discovery 4

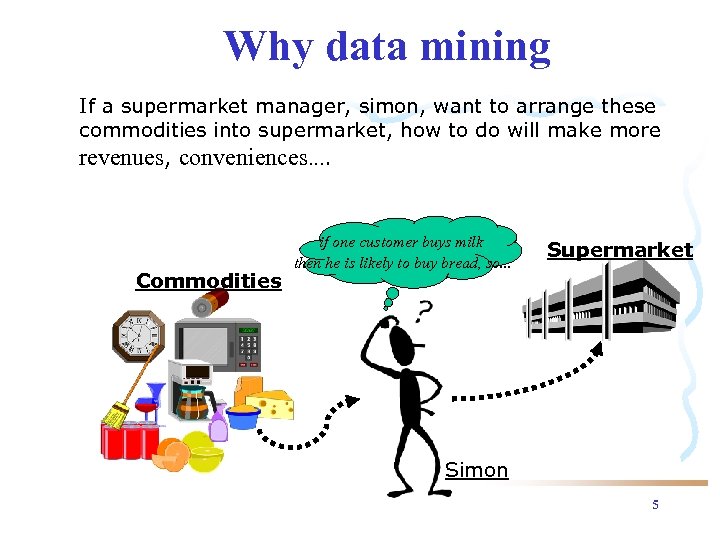Why data mining If a supermarket manager, simon, want to arrange these commodities into supermarket, how to do will make more revenues, conveniences…. Commodities if one customer buys milk then he is likely to buy bread, so. . . Supermarket Simon 5

Why data mining advertisement letters for customers, how to consider the individual differences is an important task. Before long, if simon want to send some Mary always buys diapers and milk powders, she may have a baby, so …. Simon 6

The role of Data mining Useful patterns Knowledge and strategy Preprocess data 7

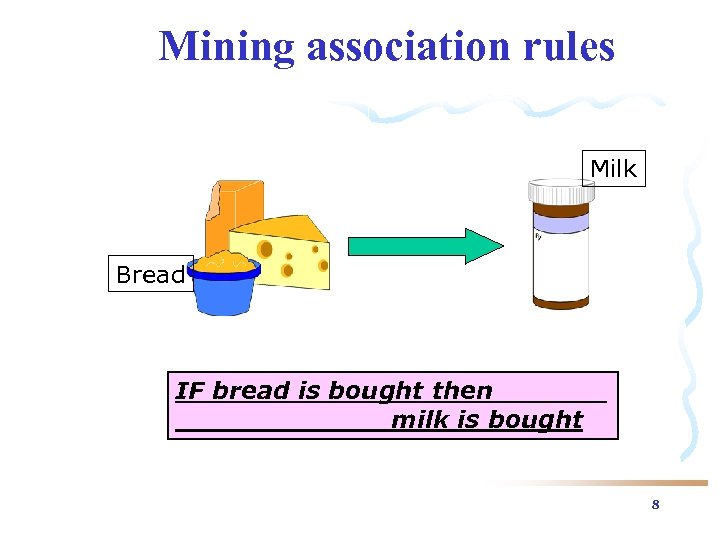Mining association rules Milk Bread IF bread is bought then milk is bought 8

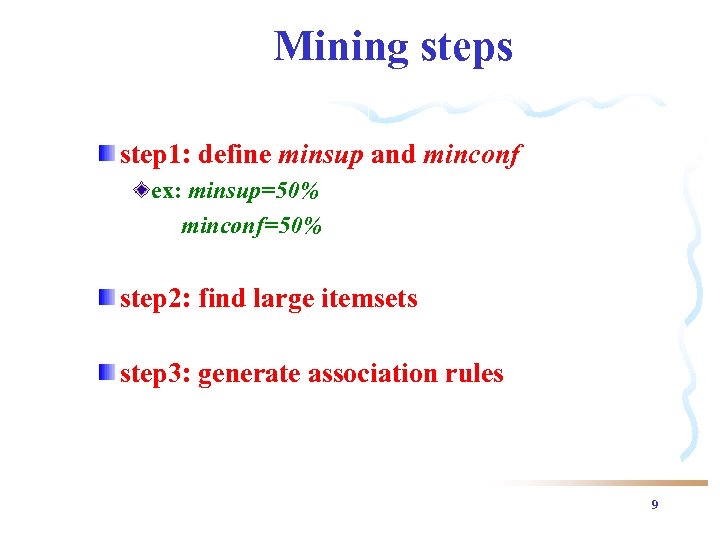Mining steps step 1: define minsup and minconf ex: minsup=50% minconf=50% step 2: find large itemsets step 3: generate association rules 9

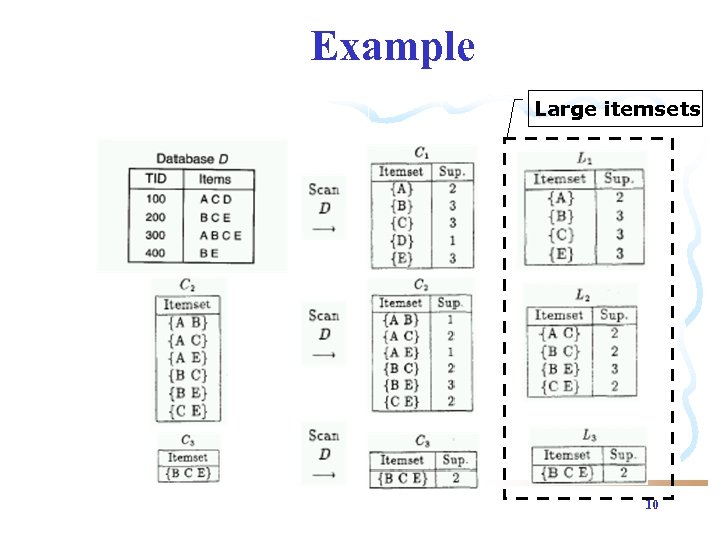Example Large itemsets 10

Outline Introduction Weights of Data Sources Rule Selection Synthesizing High-Frequency Rules Algorithm Relative Synthesizing Model Experiments Conclusion 11

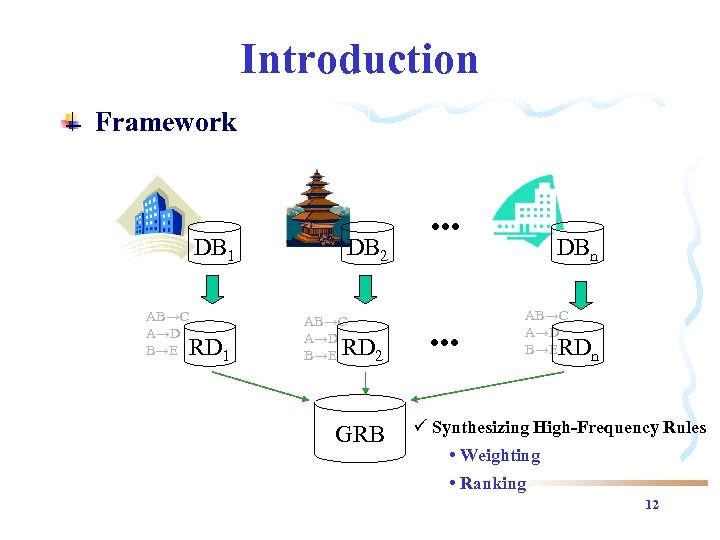Introduction Framework DB 1 AB→C A→D B→E RD 1 DB 2 AB→C A→D B→E RD 2 GRB . . . DBn AB→C A→D B→E RDn ü Synthesizing High-Frequency Rules • Weighting • Ranking 12

Weights of Data Sources Definition Di : data sources Si : set of association rules from Di Ri : association rule 3 Steps Step 1 : union of all Si Step 2 : assigning each Ri a weight Step 3 : assigning each Di a weight & normalization 13

Example 3 Data Sources (minsupp=0. 2, minconf=0. 3) S 1 S 2 S 3 AB→C with supp=0. 4, conf=0. 72 A→D with supp=0. 3, conf=0. 64 B→E with supp=0. 34, conf=0. 7 B→C with supp=0. 45, conf=0. 87 A→D with supp=0. 36, conf=0. 7 B→E with supp=0. 4, conf=0. 6 AB→C with supp=0. 5, conf=0. 82 A→D with supp=0. 25, conf=0. 62 14

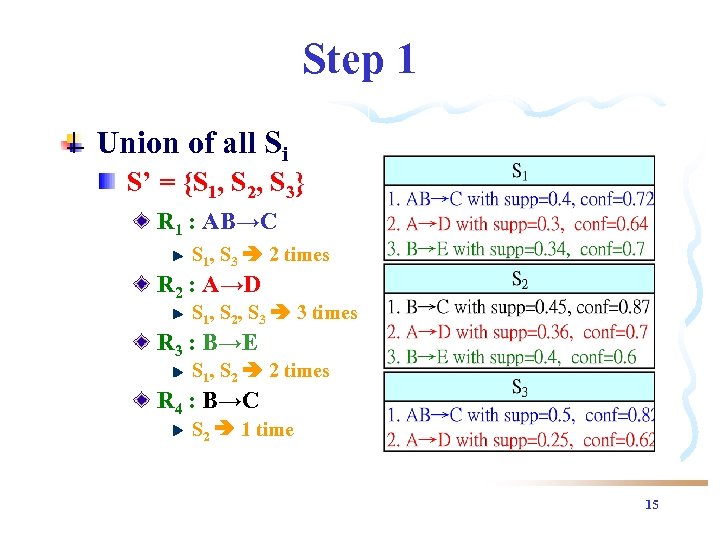Step 1 Union of all Si S’ = {S 1, S 2, S 3} R 1 : AB→C S 1, S 3 2 times R 2 : A→D S 1, S 2, S 3 3 times R 3 : B→E S 1, S 2 2 times R 4 : B→C S 2 1 time 15

Step 2 Assigning each Ri a weight R 1 WR 1 = 2 2+3+2+1 = 0. 25 WR 2 = 3 2+3+2+1 = 0. 375 WR 3 = 2 2+3+2+1 = 0. 25 WR 4 = 1 2+3+2+1 = 0. 125 R 2 R 3 R 4 16

Step 3 Assigning each Di a weight WD 1 2*0. 25+3*0. 375+2*0. 25=2. 125 WD 2 1*0. 125+2*0. 25+3*0. 375=2 WD 3 2*0. 25+3*0. 375=1. 625 Normalization WD 1 2. 125/(2. 125+2+1. 625)=0. 3695 WD 2 2/(2. 125+2+1. 625)=0. 348 WD 3 1. 625/(2. 125+2+1. 625)=0. 2825 17

Why Rule Selection ? Goal Extracting High-Frequency Rules Low-Frequency Rules Noise Solution If Num(Ri) / n < n : data sources, Num(Ri) : frequency of Ri Then Rule Ri be wiped out 18

Rule Selection Example : 10 Data Sources D 1~D 9 : {R 1 : X→Y} D 10 : {R 1 : X→Y, R 2: X 1→Y 1, …, R 11: X 10→Y 10 } Let =0. 8 Num(R 1) / 10 = 10/10 = 1 > keep Num(R 2~11) / 10 = 1/10 = 0. 1 < be wiped out WR 1 D 1~D 10 : {R 1 : X→Y} WR 1 : 10/10=1 WD 1~10 : 10*1 / 10*10*1 = 0. 1 n Num(R 1) 19

Comparison Without Rules Selection WD 1~9 0. 099 WD 10 0. 109 With Rules Selection WD 1~10 0. 1 From High-Frequency Rules Point of view Weight Errors D 1~9 |0. 1 -0. 099| 0. 001 D 10 |0. 1 -0. 109| 0. 009 Total Error = 0. 01 20

Synthesizing High-Frequency Rules Algorithm 5 Steps Step 1 : Rules Selection Step 2 : Weights of Data Sources Step 2. 1 : union of all Si Step 2. 2 : assigning each Ri a weight Step 2. 3 : assigning each Di a weight & normalization Step 3 : computing supp & conf of each Ri Step 4 : ranking all rules by support Step 5 : output the High-Frequency Rules 21

An Example 3 Data Sources =0. 4, minsupp=0. 2, minconf=0. 3 22

Step 1 Rules Selection R 1 : AB→C S 1, S 3 2 times Num(R 1) / 3 = 0. 66 keep R 2 : A→D S 1, S 2, S 3 3 times Num(R 2) / 3 = 1 keep R 3 : B→E S 1, S 2 2 times Num(R 3) / 3 = 0. 66 keep R 4 : B→C S 2 1 time Num(R 4) / 3 = 0. 33 wiped out 23

Step 2 : Weights of Data Sources Weights of Ri 2 = 0. 29 WR 1 = 2+3+2 3 = 0. 42 WR 2 = 2+3+2 2 = 0. 29 WR 2 = 2+3+2 Weight of Di WD 1 2*0. 29+3*0. 42+2*0. 29=2. 42 WD 2 3*0. 42+2*0. 29=1. 84 WD 3 2*0. 29+3*0. 42=1. 84 Normalization WD 1 2. 42/(2. 42+1. 84)=0. 3695=0. 396 WD 2 1. 84/(2. 42+1. 84)=0. 302 WD 3 1. 84/(2. 42+1. 84)=0. 302 24

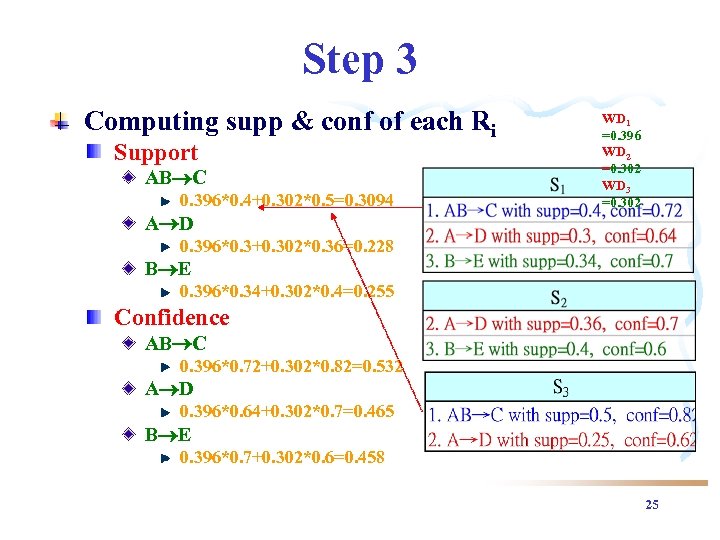Step 3 Computing supp & conf of each Ri Support AB C 0. 396*0. 4+0. 302*0. 5=0. 3094 WD 1 =0. 396 WD 2 =0. 302 WD 3 =0. 302 A D 0. 396*0. 3+0. 302*0. 36=0. 228 B E 0. 396*0. 34+0. 302*0. 4=0. 255 Confidence AB C 0. 396*0. 72+0. 302*0. 82=0. 532 A D 0. 396*0. 64+0. 302*0. 7=0. 465 B E 0. 396*0. 7+0. 302*0. 6=0. 458 25

Step 4 & Step 5 Ranking all rules by support & output minsupp=0. 2, minconf=0. 3 AB C, B E, A D Ranking 1. AB C (0. 3094) 2. B E (0. 255) 3. A D (0. 228) Output – 3 rules AB C(0. 3094, 0. 532) B E (0. 255, 0. 458) A D (0. 228, 0. 465) 26

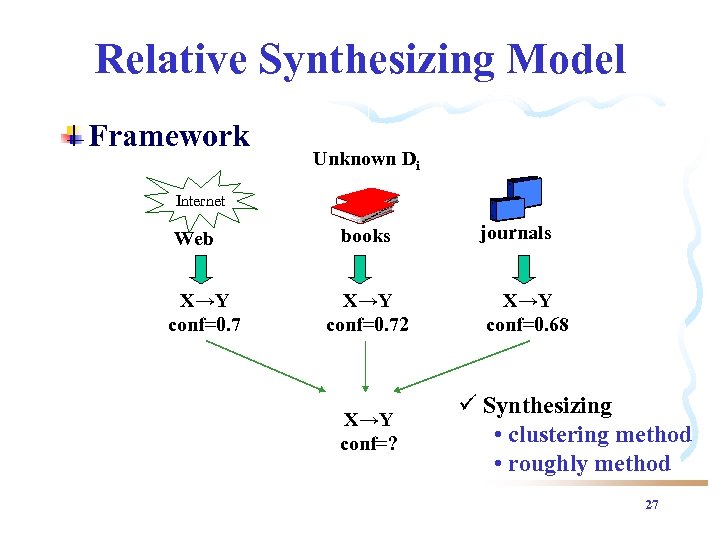Relative Synthesizing Model Framework Unknown Di Internet Web X→Y conf=0. 7 books X→Y conf=0. 72 X→Y conf=? journals X→Y conf=0. 68 ü Synthesizing • clustering method • roughly method 27

Synthesizing Methods Physical Meaning if the confidences irregularly distributed Maximum synthesizing operator Minimum synthesizing operator Average synthesizing operator if the confidences (X) normal distribution clustering interval [a, b] satisfy 1. P{ a X b } (m/n) 2. | b – a | 3. a, b > minconf. 28

Clustering Method 5 Steps Step 1 : closeness 1 - | confi – confj | The distance relation table Step 2 : closeness degree measure The confidence-confidence matrix Step 3 : two confidences close enough ? The confidence relationship matrix Step 4 : classes creating [a, b] interval of the confidence of rule X→Y Step 5 : interval verifying satisfy the constraints ? 　　　 29

An Example Assume rule X→Y conf 1=0. 7, conf 2=0. 72, conf 3=0. 68, conf 4=0. 5 conf 5=0. 71, conf 6=0. 69, conf 7=0. 7, conf 8=0. 91 3 parameters =0. 7 =0. 08 =0. 69 30

Step 1 : Closeness Example conf 1=0. 7, conf 2=0. 72 c 1, 2= 1 - | conf 1 - conf 2 | = 1 - |0. 70 -0. 72|=0. 98 31

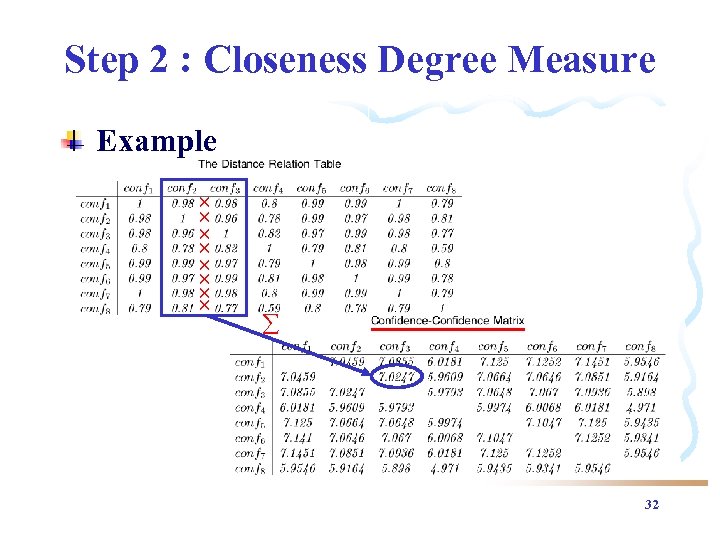Step 2 : Closeness Degree Measure Example 32

Step 3 : Close Enough ? Example =6. 9 > 6. 9 < 6. 9 33

Step 4 : Classes Creating Example 1 Class 1 : conf 1~3, conf 5~7 2 Class 2 : conf 4 3 Class 3 : conf 8 34

Step 5 : Interval Verifying Example Class 1 conf 1=0. 7, conf 2=0. 72, conf 3=0. 68, conf 5=0. 71, conf 6=0. 69, conf 7=0. 7 [min, max] = [conf 3, conf 2] = [0. 68, 0. 72] constraint 1 P{ 0. 68 X 0. 72 } (6/8) (0. 7) constraint 2 |0. 72 -0. 68| (0. 04) < (0. 08) constraint 3 0. 68, 0. 75 > minconf. (0. 65) In the same way Class 2 & Class 3 be wiped out Result X→Y : conf=[0. 68, 0. 72] Support ? In the same way Interval 35

Roughly Method Example R : AB→C supp 1=0. 4, conf 1=0. 72 supp 2=0. 5, conf 2=0. 82 Maximum max ( supp (R) )=max (0. 4, 0. 5)=0. 5 max ( conf (R) )=max (0. 72, 0. 82)=0. 82 Minimum & Average min 0. 4, 0. 72 avg 0. 45, 0. 77 36

Experiments Time SWNBS (without rules selection) SWBRS (with rules selection) SWNBS > SWBRS Error first 20 frequent itemset Max=0. 000065 Avg=0. 00003165 37

Conclusion Synthesizing Model Data Sources known weighting Data Sources unknown clustering method roughly method 38

Future works Sequence pattern Combine GA and other techniques 39