SYMMETRIC DUALITY IN OPTIMIZATION AND IT S APPLICATIONS Valery

SYMMETRIC DUALITY IN OPTIMIZATION AND IT’S APPLICATIONS Valery I. Zorkaltsev, Professor, Head of Laboratory, Energy Systems Institute Siberian Branch of the Russian Academy of Sciences E-mail: zork@isem. sei. irk. ru International conference “Optimization and applications" Montenegrio 2009 г. 1

Definition of symmetric duality For wide class of optimization problems they use special constructions called Dual optimization problems: , where primal optimization problem; dual optimization problem; transition rule (often polysemantic). 2

For dual problem one can specify problem dual to it Symmetric duality is event, when dual problem to dual problem coincides with primal problem 3

Applications of dual problems: • to prove optimality of obtained solutions; • for justification of optimization algorithms; • in solution interpretation; • for making optimization algorithms; • for researching and solving many complicated problems of operation research, including Nash equilibrium finding. 4

Lecture plan 1. Theory of symmetric duality in optimization: – Lagrangian multipliers; – Theorems of alternative systems of linear inequalities; – Legendre-Fenchel conjugate functions and their extensions. 2. Application of symmetric duality optimization algorithms and regularization in 5

Lecture plan (continuation) 3. Application in models: – load-flow models (electric circuits, hydraulic circuits, nonlinear transportation problems); – models of thermodynamic equilibrium and geometric programming; – economic equilibrium models. 6

1. Lagrange multipliers of constraints Primal problem: (1) Lagrange problem: where Lagrange multipliers, which satisfy conditions (1). Modified Lagrange problem (Sh. Churkveidze): 7

2. Theory of alternative systems of linear inequalities Any system of linear inequalities can be confronted with an alternative system of linear inequalities S by formal rules so that proposition is right: One and only one system of two is consistent: S or S*. Moreover, backward transformation takes place: and That is alternative systems S symmetric. . and S* are 8

Three examples of theorems of alternative systems of linear inequalities It is assigned: А – Rm. Sought vectors – matrix , b – vector in , . Remark. System of linear equations can be considered as special case of system of linear inequalities. The converse proposition is not correct. 9

1. Fredgolm’s theorem (about alternative systems of linear inequalities) Eithere is or there is 10

2. Farkas’ theorem Either the following system possesses a solution or the following system is solvable 11

3. Gail’s theorem Eithere is or there is vector such, that 12

Applications of alternative systems of linear inequalities theory 1. Identification of system of linear inequalities incompatibility – If a vector from the solution set of an alternative system S* will be obtained during the process of searching the solution of system S, then absence of the solution of initial system S will be proved. We have practical and effective (as computation has shown) method for identification of problem constraints inconsistency. 13

2. For determination of redundant constraints, exclusion of which doesn’t change the solution set, including situations in algorithms – Gomory or Kelly cuts; – Fourier-Chernikov convolutions for description of systems of linear inequalities solutions. 3. For identification of solutions of systems of linear inequalities with minimal set of active constraints – relative to interior points of systems of linear inequalities solution set. 14

4. For creation of new algorithms for solving systems of linear and on the basis of this nonlinear inequalities ( «Alternative approach» , which is developed by U. Evtushenko, A. Golicov). 5. All theory of linear optimization duality is contained in theorems of alternative systems of linear inequalities. Duality of linear optimization is the basis for wide class of nonlinear problems. 15

Search of solutions and identification of inconsistence of system of double-sided linear inequalities • The more restricted class of problems is considered the more interesting results about characteristics of this class of problems can be obtained • Initial system: find conditions satisfying the following • Alternative system of one inequality: find , such that where Here for vectors , have components: 16

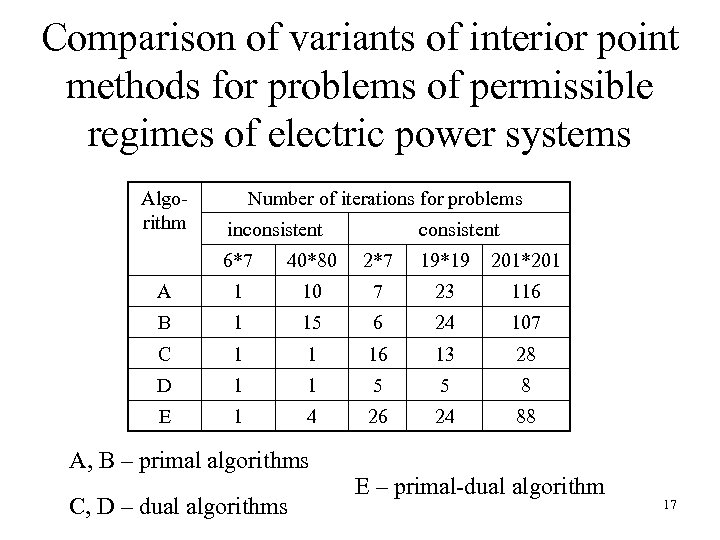Comparison of variants of interior point methods for problems of permissible regimes of electric power systems Algorithm Number of iterations for problems inconsistent 6*7 40*80 2*7 19*19 201*201 A 1 10 7 23 116 B 1 15 6 24 107 C 1 1 16 13 28 D 1 1 5 5 8 E 1 4 26 24 88 A, B – primal algorithms C, D – dual algorithms Е – primal-dual algorithm 17

Mutually dual problems of linear programming Let be sets of optimal solutions of problems (P), (P*). Let’s introduce sets of recession directions for this problems : , According to Farkas and Geil theorems pairs of sets are alternative. Symmetric duality takes place for LP problems: and 18

Theorem of duality for LP Four events are possible for problems (Р), ( 1. If , then , , , . 2. If , . Тогда , , , . 3. If , . Тогда , , , . ): 19

Theorem of duality for LP (continuation) 4. If For any There is , . Then , , , In this and only this case such that. 20

Equivalent representations of LP problem in the form of optimization problems 1. Primal problem 2. Dual problem 3. Self-dual problem 4. Symmetric problem (problem of complementarity) 21

Reresentation of a linear programming problem as a system of linear inequalities It allows to consider problems of linear programming as a special case of systems of linear inequalities. 22

3. Conjugate functions 1. Functions of each other if for is Legendre conjugate where That is 23

3. Conjugate functions 2. Functions each other, if is Fenchel conjugate of and 24

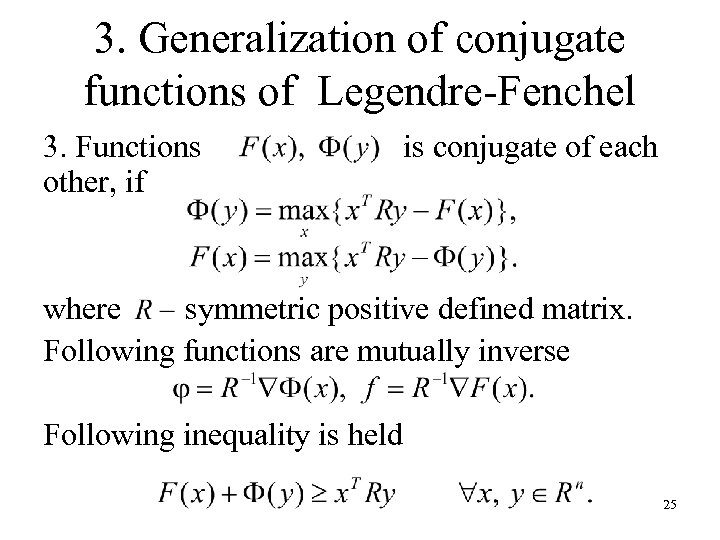3. Generalization of conjugate functions of Legendre-Fenchel 3. Functions other, if is conjugate of each where symmetric positive defined matrix. Following functions are mutually inverse Following inequality is held 25

Symmetric duality 1. Primal problem (S) (1) 2. Dual problem (S*) (2) Note: problems (S) and (S*) have different 26

Symmetric duality (continuation) 3. Self-dual problem: subject to (1), (2) 4. Symmetric problem: subject to (1), (2) 27

Symmetric duality. Equivalent system of equalities and inequalities Constraint (3) can be substituted with еquality 28

Examples I. Symmetric duality for problems of quadratic programming where positive definite matrix Mutually dual problems 29

Examples II. Especially important case of separable functions One form of writing the equivalent system of equalities and inequalities 30

Theorem (for separable ) Let fj be continious increasing functions, then (S) is a problem of minimization of strictly convex function with linear constraints, (S*), (SD) are problems of minimization of convex function with linear constraints. If, at the same time, and a system Ax=b, is consistent, then problems (S), (S*), (SD), (SS), (L) have coincident and unique (relatively to vectors x, y) solutions. Vector u is unique if rank A=m. 31

Applications, separable case 1. Regularization of problems: having small linear programming Primal problem: regularization by Tihonov Dual problem: search of pseudosolution of dual problem of linear programming 32

Applications (with and self-conjugated functions of the kind ) 2. «Alternative» way of searching for normal solutions for system of inequalities with n variables This is equivalent to problem with m variables Such approach is preferable when 33

Applications 3. Load-flow models (nonlinear transportation problems, electric circuits, hydraulic circuits including heat, water and gas delivery problems) indices of nodes, indices of arcs, incedence matrix, vector of volumes of delivery in system and out of system, 34

Load-flow models in losses, vector of pressure gains (or electromotive forces, or conveyance tariffs) on arcs, vector of flows on arcs, vector of pressures (tensions, prices) nodes, vector of pressure losses (tension price rises) on arcs. 35

Load-flow models arcs, pressure flow balance in nodes (first Kirchhoff law), balances of pressures on interrelations of loss and flow on arcs. For example, Ohm law, Darcy law. 36

Results for hydraulic circuits obtained using theory of symmetric duality 1. Conditions for existence and uniqueness of classical load-flow model solution are clarified. 2. Possibilities for choosing the form of mathematical models representation are expanded. 3. Foundations for constructing and theoretical justification of algorithms for solving load-flow problems are obtained. 37

Results for hydraulic circuits obtained using theory of symmetric duality 4. Theoretical research is held (including clarification of conditions for existence and uniqueness), algorithms for solving nonclassical load-flow problems are developed, where some components of vectors x, y, u, b and c may be fixed аnd other components of these vectors should be found. 38

Transport model with piecewise defined nonlinear costs • Model is applied in analysis of operation of natural gas and oil delivery systems to find and eliminate bottlenecks in proper time. • Let be flow through the arc j, − costs coefficient for the arc j, , − nonlinear function. For each arc costs function will be 39

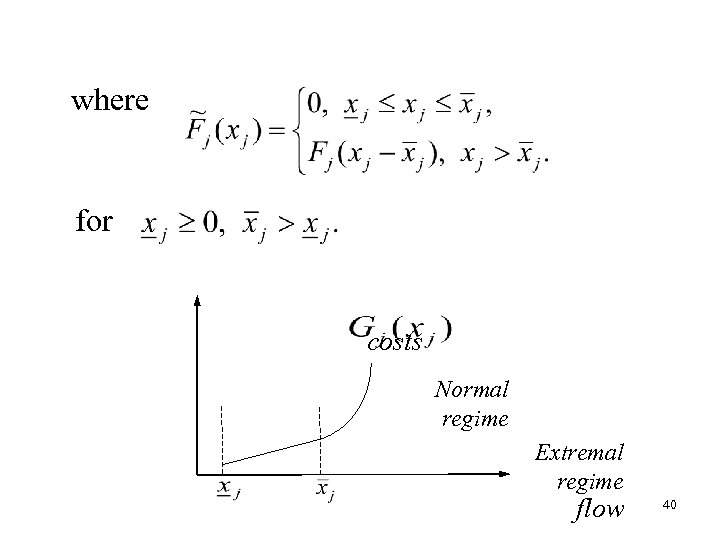where for costs Normal regime Extremal regime flow 40

Primal optimization problem • bi – volume of delivery into the net at source node (if ) or out of the net at consumer node (if ), • hi – penalty for incomplete delivery in node i, • Isrc – set of numbers of source nodes, • Icons – set of numbers of consumer nodes. 41

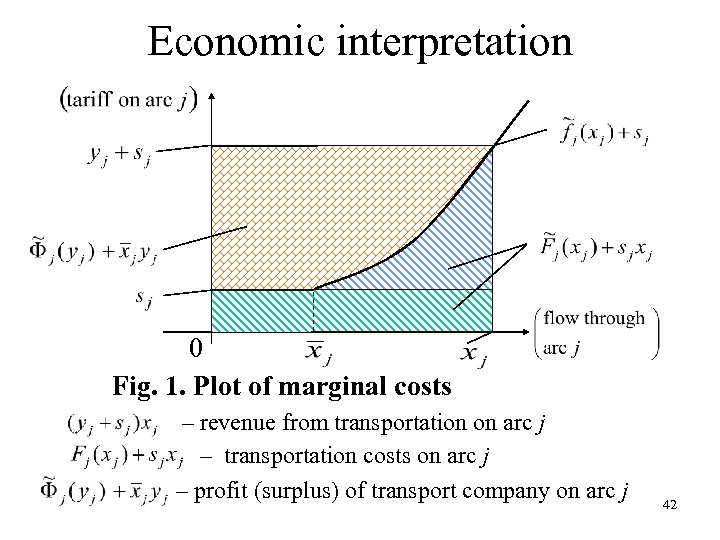Economic interpretation 0 Fig. 1. Plot of marginal costs – revenue from transportation on arc j – transportation costs on arc j – profit (surplus) of transport company on arc j 42

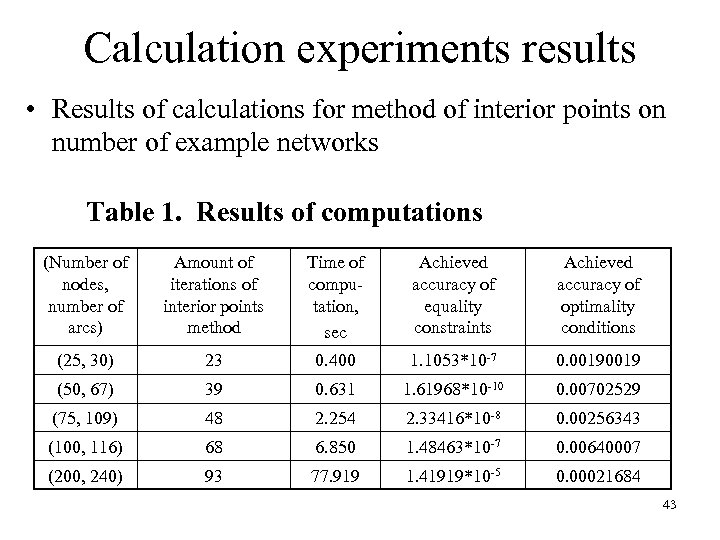Calculation experiments results • Results of calculations for method of interior points on number of example networks Table 1. Results of computations (Number of nodes, number of arcs) Amount of iterations of interior points method Time of computation, sec Achieved accuracy of equality constraints Achieved accuracy of optimality conditions (25, 30) 23 0. 400 1. 1053*10 -7 0. 0019 (50, 67) 39 0. 631 1. 61968*10 -10 0. 00702529 (75, 109) 48 2. 254 2. 33416*10 -8 0. 00256343 (100, 116) 68 6. 850 1. 48463*10 -7 0. 00640007 (200, 240) 93 77. 919 1. 41919*10 -5 0. 00021684 43

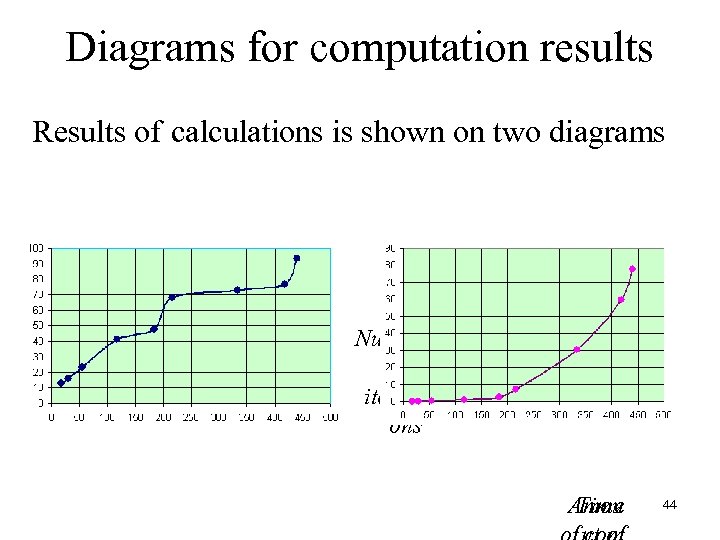Diagrams for computation results Results of calculations is shown on two diagrams Numbe r of iterati ons Time Amou 44

Problem of finding bottlenecks in natural gas delivery network in order to obtain system reliability • Two examples were computed for real networks: – Aggregated network for natural gas delivery system (21 nodes, 28 arcs) – Detailed network for the same system (337 nodes, 589 arcs) • Two aims of computation for each example: – 1) to determine nodes with low supply and arcs with utilized capacity when only normal regime is allowed – 2) to determine abilities to increase supply of nodes with low supply and find arcs switched to extremal regime when extremal regime is allowed 45

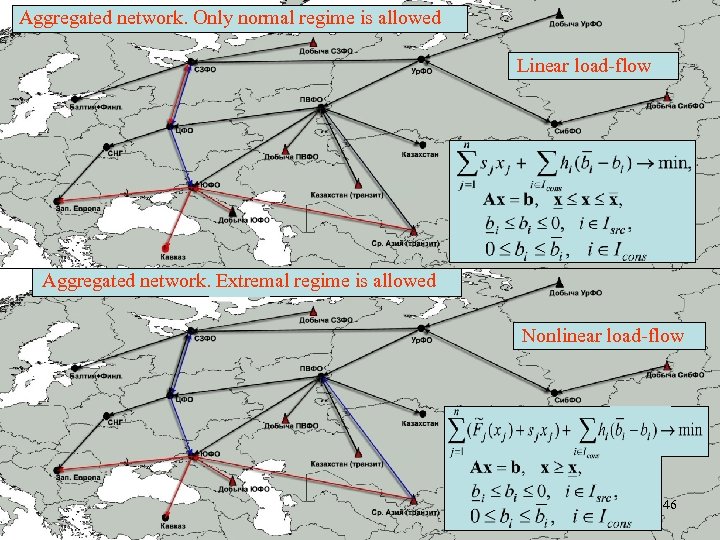Aggregated network. Only normal regime is allowed Linear load-flow Aggregated network. Extremal regime is allowed Nonlinear load-flow 46

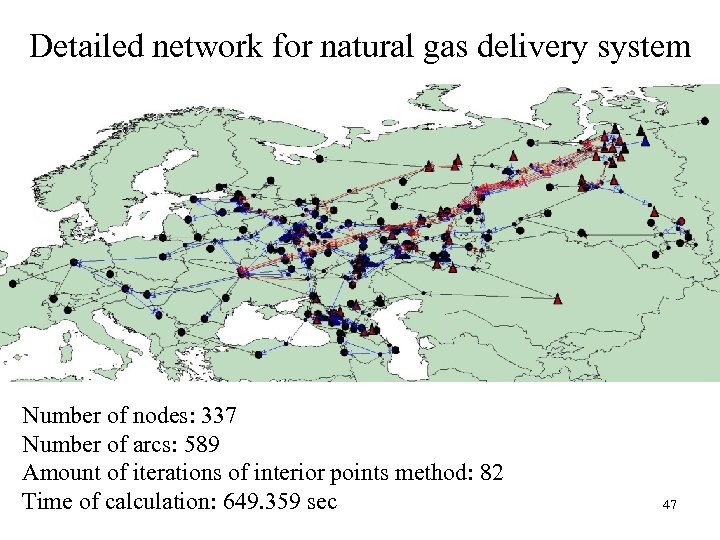Detailed network for natural gas delivery system Number of nodes: 337 Number of arcs: 589 Amount of iterations of interior points method: 82 Time of calculation: 649. 359 sec 47

Final word • I’d like to give thank to people who helped me make this report: – Perjabinsky Sergey, – Medvezhonkov Dmitry. • Thank you for your attention! 48