Symbolically Computing Most-Precise Abstract Operations for Shape Analysis

Symbolically Computing Most-Precise Abstract Operations for Shape Analysis Greta Yorsh Tel Aviv University Thomas Reps University of Wisconsin Mooly Sagiv Tel Aviv University Symbolically computing most-precise abstract operations for April analysis shape 2004 TACAS'04 TACAS’ 04

Motivation n New approach to using symbolic techniques in abstract interpretation – for shape analysis – for other analyses n What does it mean to harness a decision procedure for use in static analysis? – what are the requirements ? – what does it buy us ? 2 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

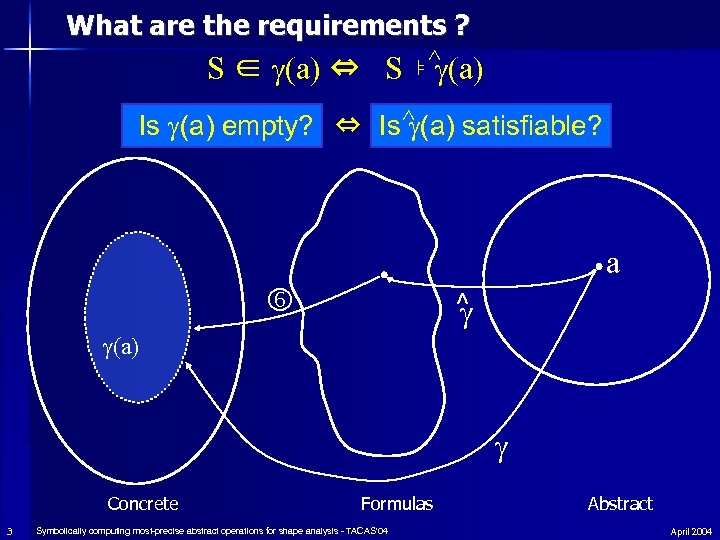
What are the requirements ? S ∈ (a) ⇔ S ⊧ ^ (a) Is (a) empty? ⇔ Is ^ (a) satisfiable? a ^ (a) Concrete 3 Formulas Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 Abstract April 2004

What does it buy us ? n Guarantee the most-precise result w. r. t. to the abstraction – best transformer – other abstract operations n Modular reasoning – assume-guarantee reasoning – scalability 4 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

$Assume-Guarantee Reasoning ^ Is (a)⇒ valid? {prebar, postbar} T bar(); {prefoo, postfoo} void foo()$

Assume-Guarantee Reasoning ^ Is (a)⇒ valid? {prebar, postbar} T bar(); {prefoo, postfoo} void foo() { assume[prefoo]; T p; . . . assert[prebar]; -----p = bar(); assume[postbar]; . . . assert[postfoo]; } 5 <⊤> <a 1> assert[ ](a) <a 2> assume[ ](a) <a 3> <a 4> Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 ? April 2004

The assume[ ](a) Operation ^ (a) ) ( ^ assume[ ](a) = ( (a) X ^ a Concrete 6 Formulas Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 Abstract April 2004

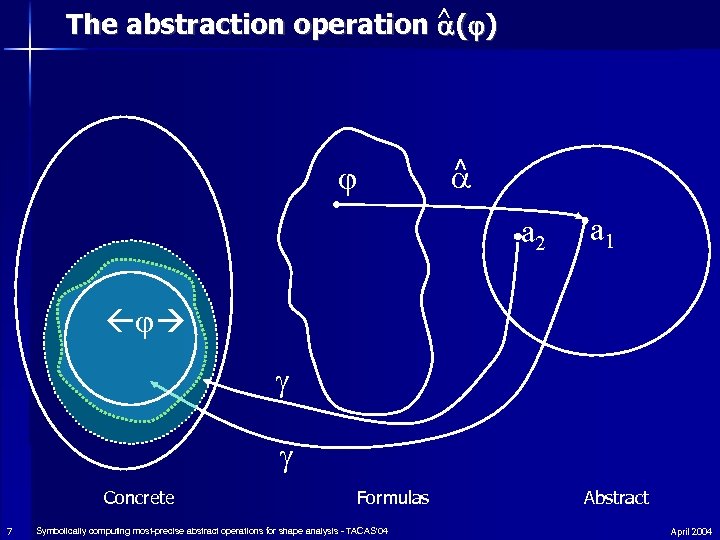
The abstraction operation ^ ( ) ^ a 2 a 1 Concrete 7 Formulas Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 Abstract April 2004

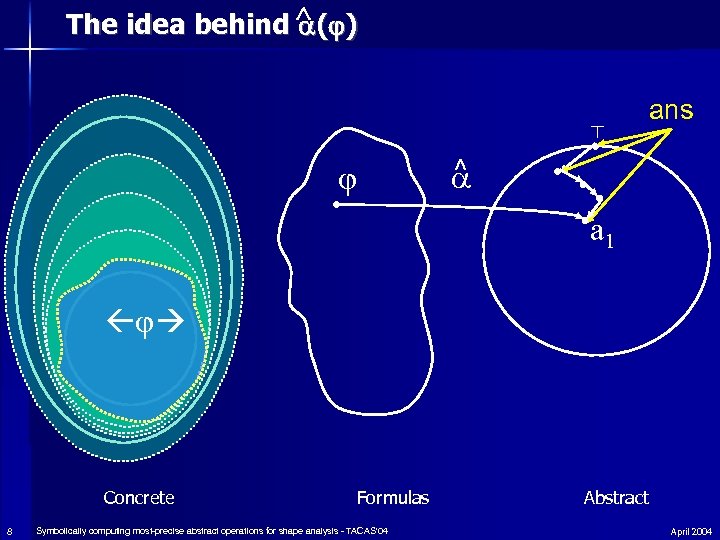
The idea behind ^ ( ) ⊤ ans ^ a 1 Concrete 8 Formulas Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 Abstract April 2004

Reminder of the talk n Shape analysis – Canonical abstraction n ^ Algorithm for abstraction - example ^ Abstract operations using n Further work n 9 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

Shape Analysis n Static program analysis n Determine “shape invariants” – all possible memory configurations n Can be used to – Verify programs (partially) – Detect memory errors – Prove properties about dynamically allocated data – Detect logical errors – Code optimizations 10 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

Why is Shape Analysis Difficult? n Destructive updating through pointers – p next = q – Produces complicated aliasing relationships n Dynamic memory allocation – No bound on the size of run-time data structures n 11 Abstract domain of 3 -valued structures with canonical abstraction [Sagiv, Reps, Wilhelm] Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

3 -Valued Logical Structures n Relation meaning over {0, 1, ½} n Kleene – 1: True – 0: False – n ½ : Unknown A join semi-lattice: 0 ⊔ 1 = ½ ½ 12 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

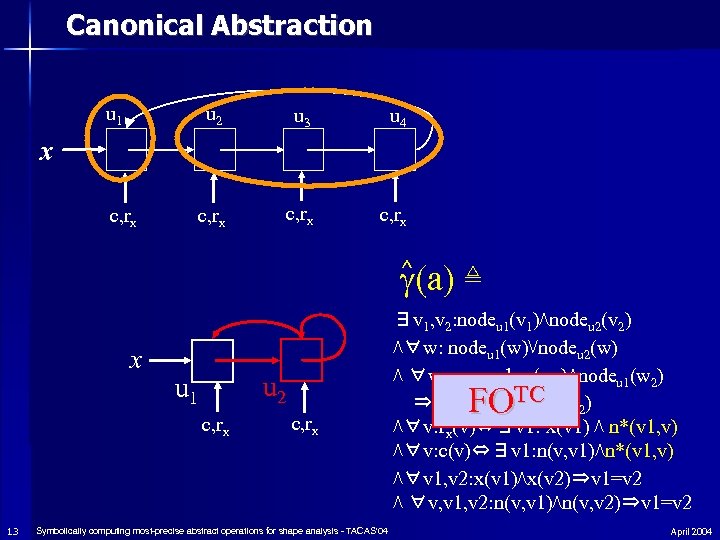
Canonical Abstraction u 1 u 2 u 3 u 4 c, rx x c, rx ^ (a) ≜ x u 2 u 1 c, rx 13 c, rx Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 ∃v 1, v 2: nodeu 1(v 1)⋀nodeu 2(v 2) ⋀∀w: nodeu 1(w)⋁nodeu 2(w) ⋀ ∀w 1, w 2: nodeu 1(w 1)⋀nodeu 1(w 2) TC ⇒(w 1=w 2)⋀⌝n(w 1, w 2) ⋀∀v: rx(v)⇔∃v 1: x(v 1) ⋀ n*(v 1, v) ⋀∀v: c(v)⇔∃v 1: n(v, v 1)⋀n*(v 1, v) ⋀∀v 1, v 2: x(v 1)⋀x(v 2)⇒v 1=v 2 ⋀ ∀v, v 1, v 2: n(v, v 1)⋀n(v, v 2)⇒v 1=v 2 FO April 2004

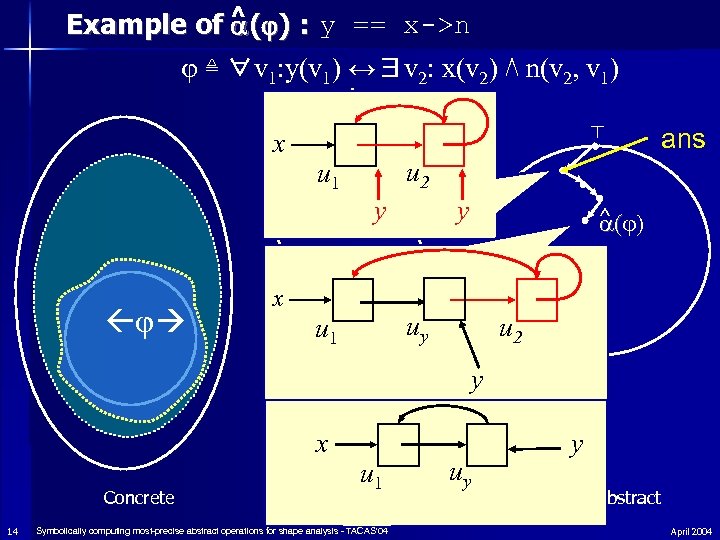
Example of ^ ( ) : y == x->n ≜ ∀v 1: y(v 1) ↔∃v 2: x(v 2) ⋀ n(v 2, v 1) x x x ⊤ u 1 ans u 2 y y ^ ( ) uy u 1 u 2 y x Concrete 14 u 1 Formulas Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 uy y Abstract April 2004

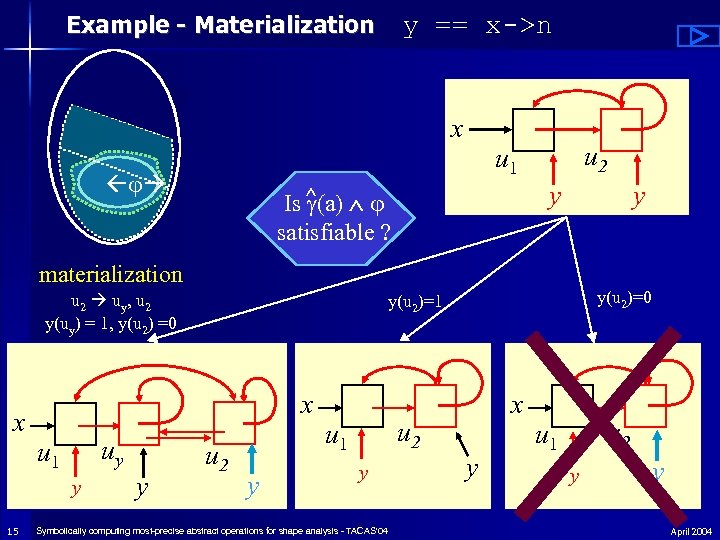
Example - Materialization y == x->n x u 2 u 1 y Is ^ (a) satisfiable ? y materialization u 2 uy, u 2 y(uy) = 1, y(u 2) =0 x x uy u 1 y 15 y y(u 2)=0 y(u 2)=1 u 2 y u 2 u 1 y Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 x y u 2 u 1 y y April 2004

Abstract Operations n ^ ( ) – best abstract value that represents n What does it buy us ? n ^ ^ assume[ ](a) = ( (a) ⋀ ) assume[ – assume-guarantee reasoning – pre- and post-conditions specified by logical formulas ^ ^ ( n BT(t, a) = ( ^ extend(a)) ⋀ t ) – best abstract transformer – parametric abstractions n 17 ^ ( meet(a 1, a 2) = ( ^ a 1) ⋀ ^ a 2) ) ( Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

SPASS Experience n Handles arbitrary FO formulas n Can diverge – use timeout n Converges in our examples – Captures older shape analysis algorithms n How to handle FOTC ? – Overapproximations lead to too many structures 18 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

Decidable Transitive-closure Logic n Neil Immerman (UMASS), Alexander Rabinovich (TAU) n ∃∀(TC, f) is subset of FOTC – exist-forall form – arbitrary unary relations – single function f n Decidable for satisfiability – NEXPTIME-complete n n 19 Any “reasonable” extension is undecidable Rather limited Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

Simulation Technique – CAV’ 04 n Neil Immerman (UMASS), Alexander Rabinovich (TAU) n Simulate realistic data structures using decidable logic over tractable structures – Singly linked list - shared/cyclic/nested – Doubly linked list – Trees n n 20 Preserved under mutations Abstract interpretation, Hoare-style verification Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004

Further Work n Implementation n Decidable logic for shape analysis n Assume-guarantee of “real” programs – case study: Java Collection – specification language – write procedure specifications n Extend to other domains – Infinite-height gretay www. cs. tau. ac. il/~gretay 21 Symbolically computing most-precise abstract operations for shape analysis - TACAS'04 April 2004