4dfe30bc42f2a1988377078dd2be879d.ppt
- Количество слайдов: 99

Syllabus for 2 GLSS, Galaxies and Large Scale Structures. Dr. P. H. Regan, 29 BC 04, x 6783 p. regan@surrey. ac. uk Spring Semester Books 1) Discovering Astronomy, Robins, Jefferys and Shawl, Wiley, (RJS) 2) An Introduction to Modern Astrophysics, Carroll and Osterlie, Wiley (CO) 3) Introductory Astronomy, Haliday, Wiley (HAL) 4) Active Galactic Nuclei, Robson, Wiley, (ROB) 5) Large-Scale Structures in the Universe, Fairall, Wiley (FAI) 2 GLSS P. H. Regan 1

n 2 GLSS Course Outline Perspectives – Size scales – Nuclei and atoms – interstellar medium – Standard Model n Galaxies – Milky Way – Galaxy types, spirals, ellipticals. . . – Colliding Galaxies n Large Scale Structure – Hubble’s Law – Recognition of large scale structures n Active Galaxies – Active Galactic Nuclei – Gamma-ray bursters 2 GLSS P. H. Regan 2

Is the Universe Infinite ? Olber’s Paradox (RJS p 534, CO p 1222) Q. Why is the sky dark at night ? If the universe was infinitely large and old, you would see a star in your line of sight in all directions, the night sky should be bright! This is evidently NOT the case, ‘Olber’s Paradox’. Olber’s ‘solution’, space not transparent BUT this wouldn’t matter as any interstellar dust would be heated to the same temp. as stellar surface and thus glow the same colour. Also proposed was that the recession velocity moved the light out of visible wavelengths (‘redshifted’), BUT the shift is not large enough. A. Light has a finite speed (c=3 x 108 ms-1) and the light from the furthest stars has not reached the earth yet (solution proposed by Lord Kelvin and Edgar Allen Poe!) Thus the observable universe is finite in size (and age). 2 GLSS P. H. Regan 3

Size Scales • Nuclei approx 10 -15 m, stellar fuel. • Atoms approx 10 -10 m, cosmic probes • People approx 1 m, cosmic observers • Stars approx 104 m->1012 m cosmic furnaces • Galaxies approx 1019 m->1021 m (this course) Units of Distance (RJS p 320, CO p 64) 1 astronomical unit (AU) = 1. 5 x 1011 m (= earth - sun distance) 1 Parsec =3. 1 x 1016 m (=1 parallax second) d (pc) = 1 Au / p (in seconds of arc) 1 light year (ly) = 9. 5 x 1015 m (=distance light travelled in 1 year) Ro = 7. 0 x 108 m (= solar radius) RO = 8. 0(5)kpc (= sun -> centre of galaxy) 2 GLSS P. H. Regan 4
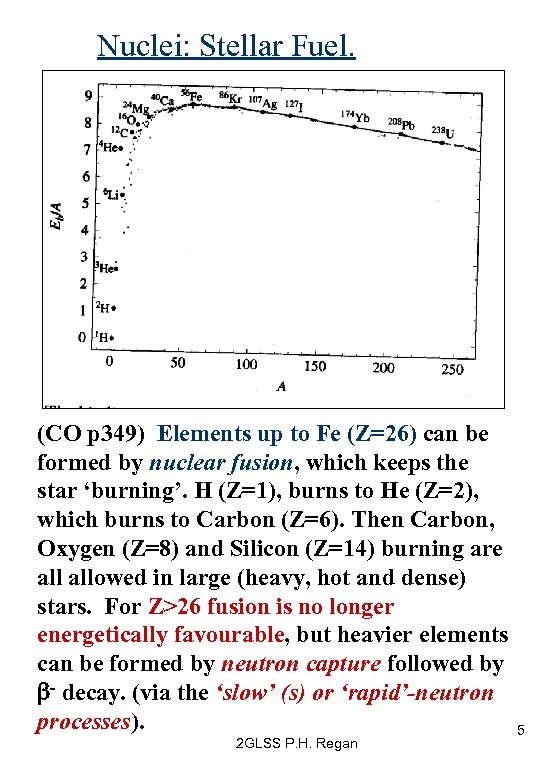
Nuclei: Stellar Fuel. (CO p 349) Elements up to Fe (Z=26) can be formed by nuclear fusion, which keeps the star ‘burning’. H (Z=1), burns to He (Z=2), which burns to Carbon (Z=6). Then Carbon, Oxygen (Z=8) and Silicon (Z=14) burning are allowed in large (heavy, hot and dense) stars. For Z>26 fusion is no longer energetically favourable, but heavier elements can be formed by neutron capture followed by b- decay. (via the ‘slow’ (s) or ‘rapid’-neutron processes). 2 GLSS P. H. Regan 5
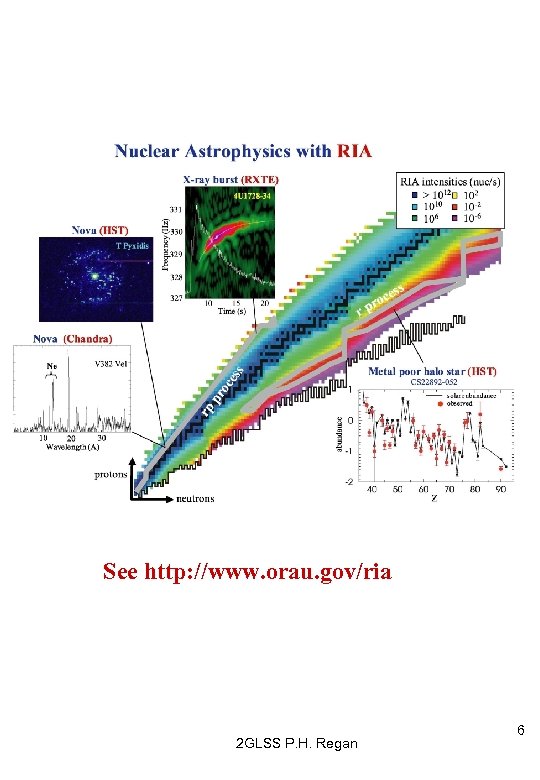
See http: //www. orau. gov/ria 2 GLSS P. H. Regan 6
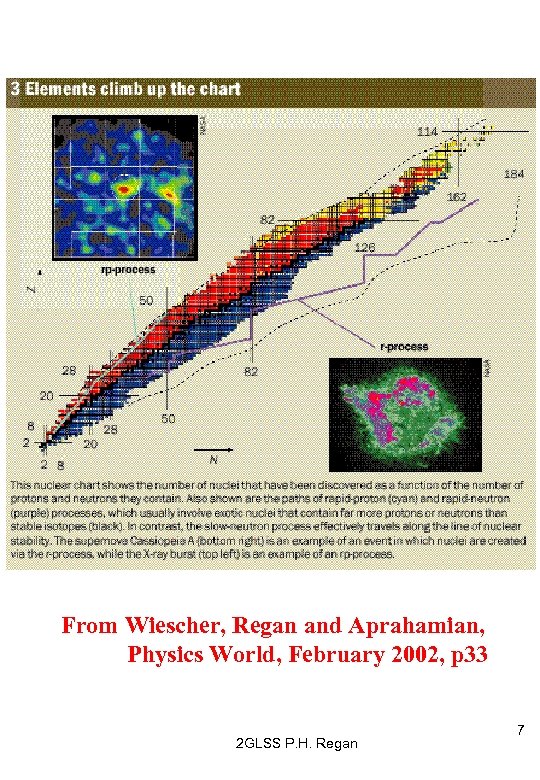
From Wiescher, Regan and Aprahamian, Physics World, February 2002, p 33 2 GLSS P. H. Regan 7
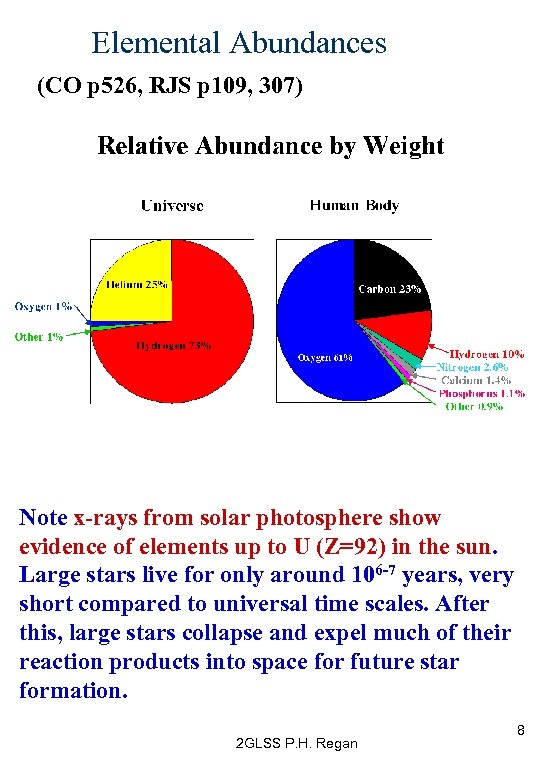
Elemental Abundances (CO p 526, RJS p 109, 307) Note x-rays from solar photosphere show evidence of elements up to U (Z=92) in the sun. Large stars live for only around 106 -7 years, very short compared to universal time scales. After this, large stars collapse and expel much of their reaction products into space for future star formation. 2 GLSS P. H. Regan 8
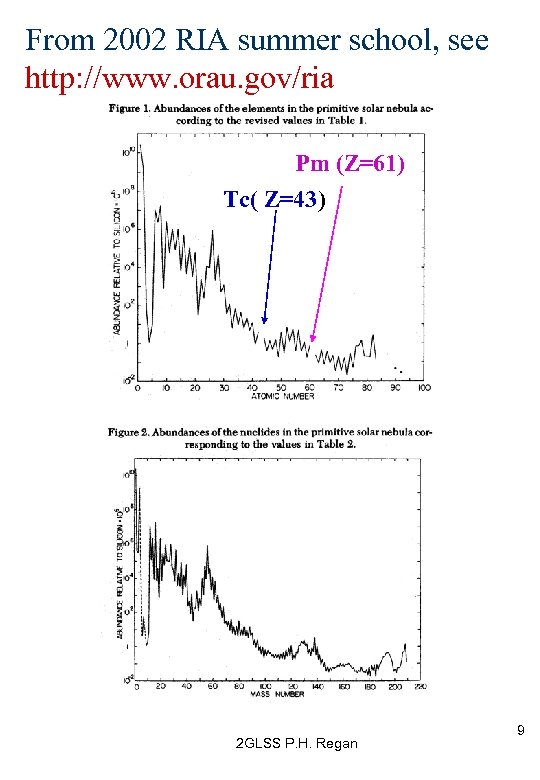
From 2002 RIA summer school, see http: //www. orau. gov/ria Pm (Z=61) Tc( Z=43) 2 GLSS P. H. Regan 9
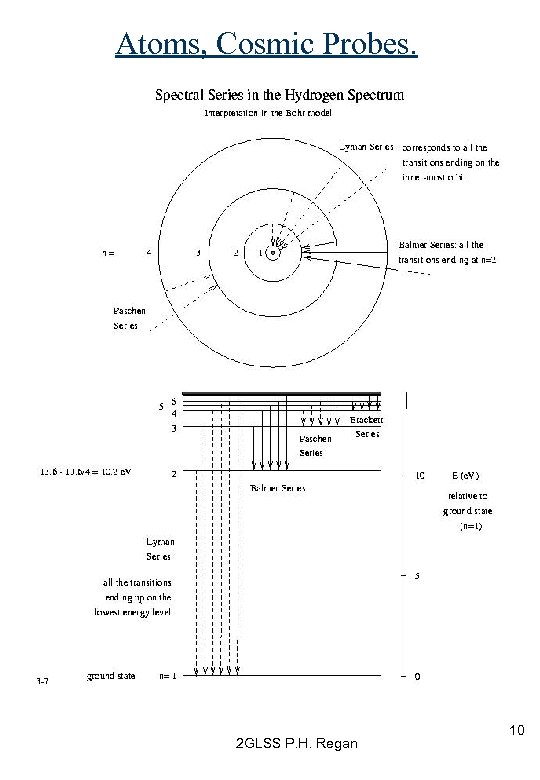
Atoms, Cosmic Probes. 2 GLSS P. H. Regan 10
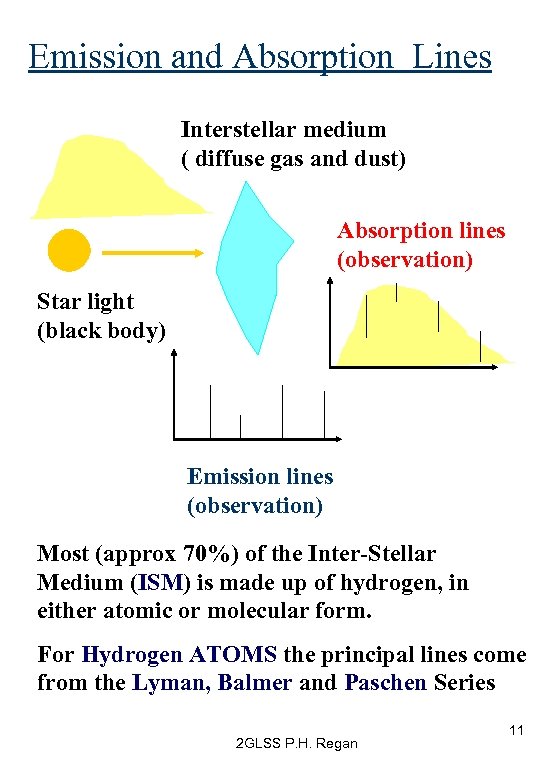
Emission and Absorption Lines Interstellar medium ( diffuse gas and dust) Absorption lines (observation) Star light (black body) Emission lines (observation) Most (approx 70%) of the Inter-Stellar Medium (ISM) is made up of hydrogen, in either atomic or molecular form. For Hydrogen ATOMS the principal lines come from the Lyman, Balmer and Paschen Series 2 GLSS P. H. Regan 11

• A hot, dense gas (or solid object) produces a continuous spectrum with no dark spectral lines. (Black-body spectrum) • A hot, diffuse gas produces bright emission lines when an electron makes a transition from a higher excited state to a lower one. The wavelength of the emitted photon can be calculated from the energy difference between the initial and final levels. • A cool diffuse gas in front of a black-body source produces dark, absorption lines when an electron is raised from a low-excitation energy orbit to a higher one. 2 GLSS P. H. Regan 12
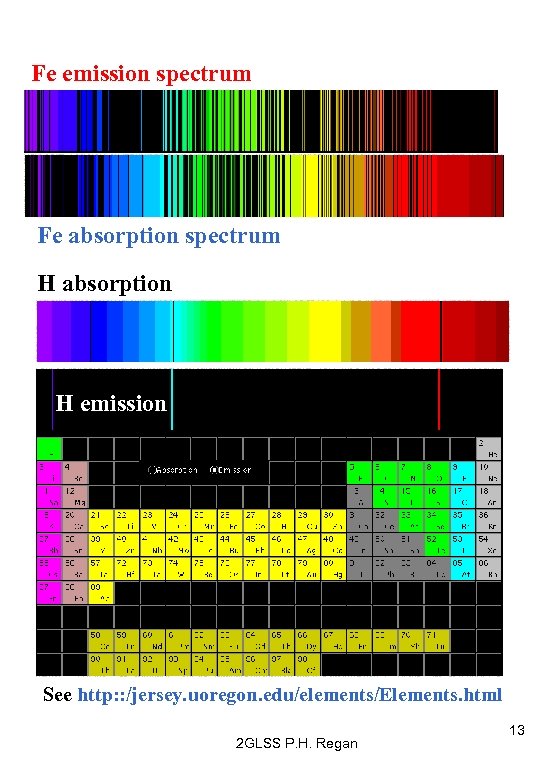
Fe emission spectrum Fe absorption spectrum H absorption H emission See http: : /jersey. uoregon. edu/elements/Elements. html 2 GLSS P. H. Regan 13
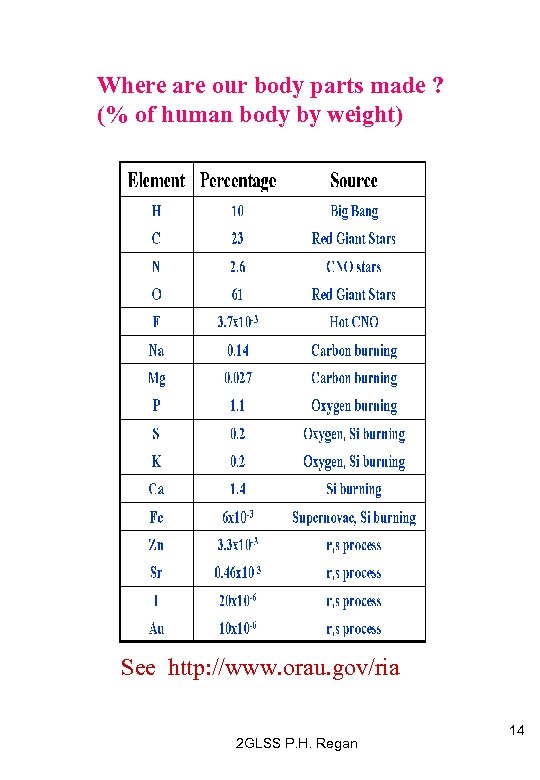
Where are our body parts made ? (% of human body by weight) See http: //www. orau. gov/ria 2 GLSS P. H. Regan 14
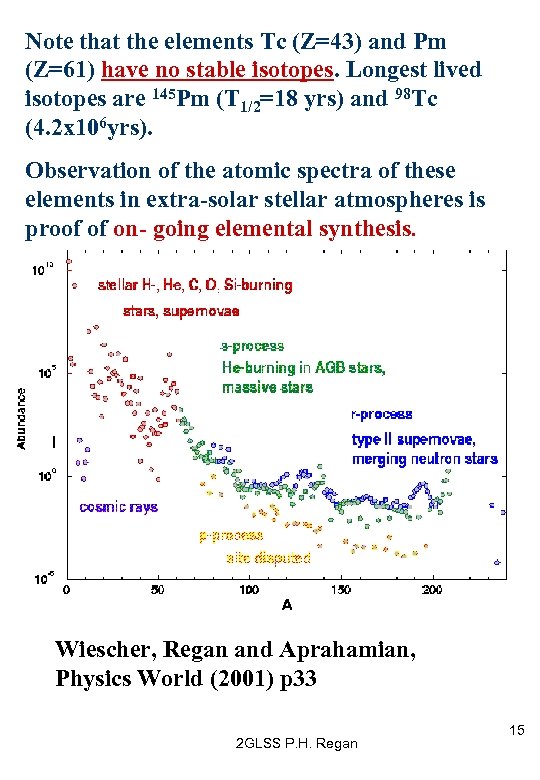
Note that the elements Tc (Z=43) and Pm (Z=61) have no stable isotopes. Longest lived isotopes are 145 Pm (T 1/2=18 yrs) and 98 Tc (4. 2 x 106 yrs). Observation of the atomic spectra of these elements in extra-solar stellar atmospheres is proof of on- going elemental synthesis. Wiescher, Regan and Aprahamian, Physics World (2001) p 33 2 GLSS P. H. Regan 15
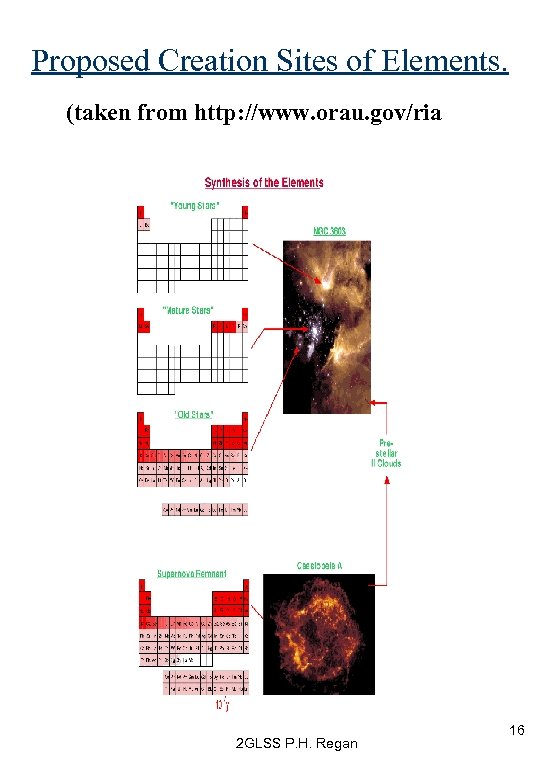
Proposed Creation Sites of Elements. (taken from http: //www. orau. gov/ria 2 GLSS P. H. Regan 16
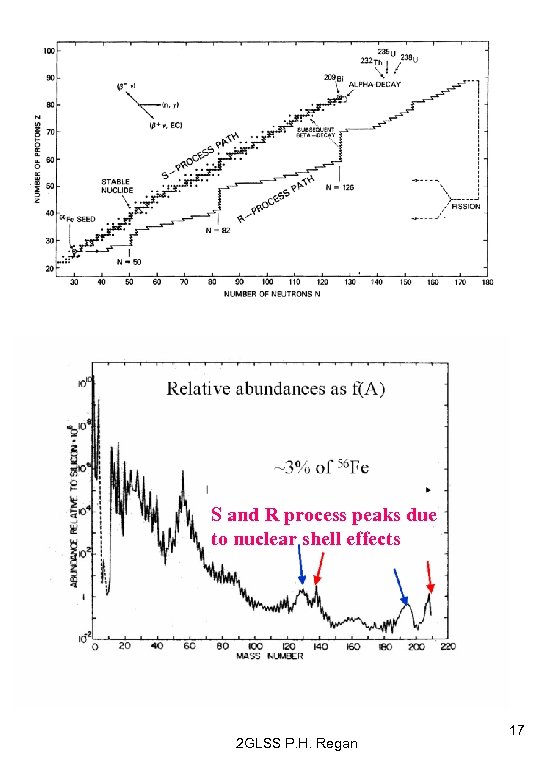
S and R process peaks due to nuclear shell effects 2 GLSS P. H. Regan 17

Metallicity (CO p 920) The iron (Fe, Z=26) content can be used as a good indicator of the age of the star. Newer stars have a higher iron content than their predecessors (more generations of reactions). The metallicity is defined as the iron-to-hydrogen (Fe: H) ratio in the atmosphere of a star compared to the solar value. This is given by the expression [Fe/H] = log 10 (NFe/NH) - log 10(NFe/NH)o where log 10(NFe/NH)o corresponds to the solar value. This stars with metallicities identical to the sun’s have [Fe/H]=0. Typical values range from -4. 5 for old, metal-poor stars, to +1 for young, metal-rich ones. Note that some astronomers believe Type 1 a supernovas may distort the local values of the [Fe/H] ratio for different regions of the inter-stellar medium (ISM) and thus prefer the [O/H] ratio instead as an measure of stellar age. 2 GLSS P. H. Regan 18

Forbidden Lines, ‘Metastable states, ‘isomers’ CO p 404, Certain transitions from excited atomic and molecular states are hindered in their decay, usually by some quantum mechanical decay selection rule. This can give rise to very long lifetimes for such states. For such atomic states to exist in interstellar gas etc. the density must be very small since (as on earth) random atomic collisions would deexcite this state. Examples of such states at the l=21 cm decay in the neutral hydrogen atom (H-I) and the green glow associated with some nebular arising from emissions in doubly ionised oxygen (O-III). 2 GLSS P. H. Regan 19
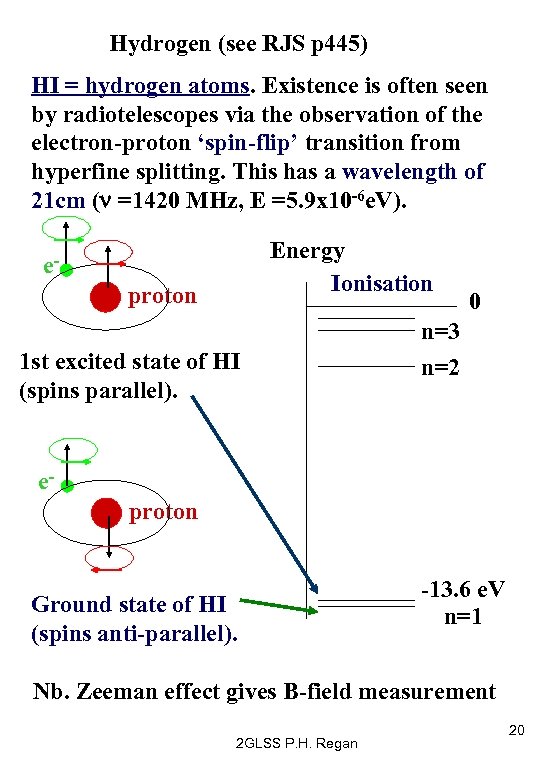
Hydrogen (see RJS p 445) HI = hydrogen atoms. Existence is often seen by radiotelescopes via the observation of the electron-proton ‘spin-flip’ transition from hyperfine splitting. This has a wavelength of 21 cm (n =1420 MHz, E =5. 9 x 10 -6 e. V). Energy Ionisation eproton 1 st excited state of HI (spins parallel). 0 n=3 n=2 eproton Ground state of HI (spins anti-parallel). -13. 6 e. V n=1 Nb. Zeeman effect gives B-field measurement 2 GLSS P. H. Regan 20

Hendrik Van de Hulst’s prediction of the observation of the 21 cm line allowed the study of cold, neutral hydrogen in the cosmos. If H atoms collide with neighbouring atoms, the atom can be raised from its anti-parallel spins ground state to the excited, parallel-spin config. This is a low-energy, excited metastable state (~107 years due to non-conservation of spin, 1 s>1 s, but photon has intrinsic spin 1). Due to the low density, the atom can remain in this state for a long time before decaying back to the ground state via the 21 cm emission. This discovery was important because • It’s a feature of H (most abundant element) • It occurs only in low density regions • It indicates the presence of neutral ( i. e. nonionised and non-molecular) HI atoms • It is not easily absorbed by interstellar gas. This means that 21 cm radiation emission fromalmost anywhere in the galaxy can be measured on earth via radiotelescopes. 2 GLSS P. H. Regan 21
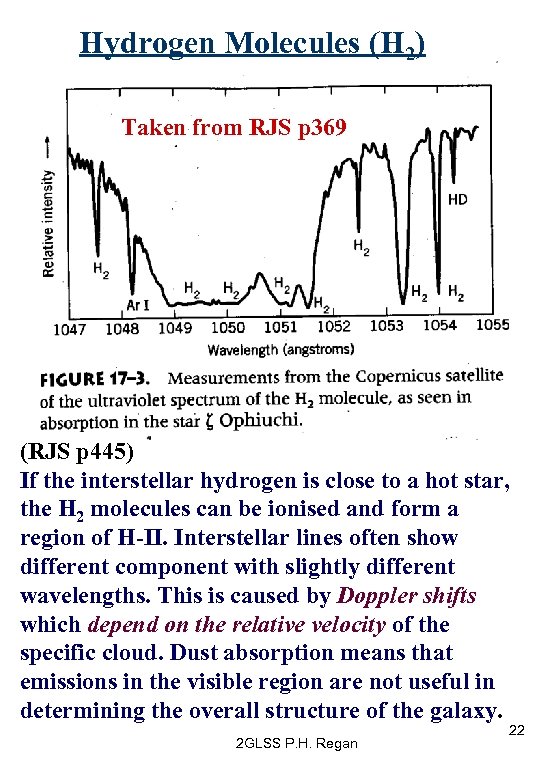
Hydrogen Molecules (H 2) Taken from RJS p 369 (RJS p 445) If the interstellar hydrogen is close to a hot star, the H 2 molecules can be ionised and form a region of H-II. Interstellar lines often show different component with slightly different wavelengths. This is caused by Doppler shifts which depend on the relative velocity of the specific cloud. Dust absorption means that emissions in the visible region are not useful in determining the overall structure of the galaxy. 2 GLSS P. H. Regan 22
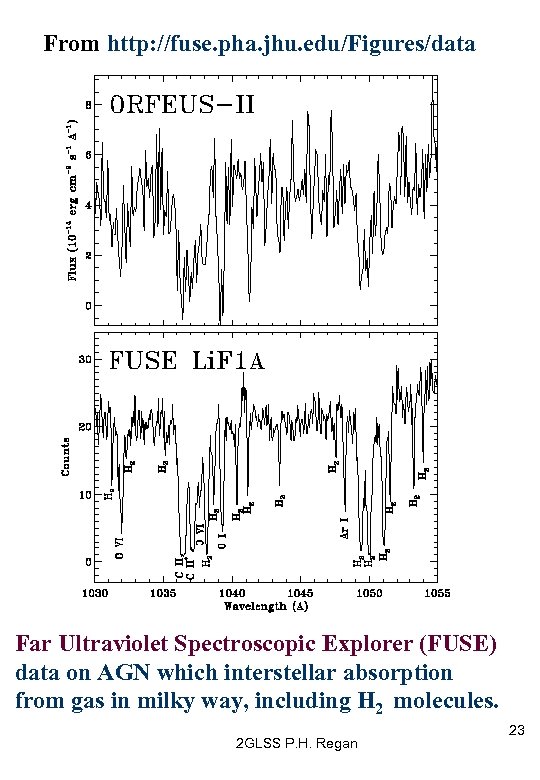
From http: //fuse. pha. jhu. edu/Figures/data Far Ultraviolet Spectroscopic Explorer (FUSE) data on AGN which interstellar absorption from gas in milky way, including H 2 molecules. 2 GLSS P. H. Regan 23

The Interstellar Medium (ISM) • Importance of radio-astronomy in seeing further due to less scattering/absorption in interstellar dust. • Interstellar dust is heated to approx. 10 -90 k by the stars in the galaxy, which then radiated in the far infra-red region (30 -300 mm). • Stars radiate strongly in the near infrared region (1 -10 mm). Very little stellar ‘extinction’ of light (as which occurs for the visible region) occurs in this range. See e. g. , COBE spectra. • Spin-flip transition in hydrogen gives rise to a 21 cm radiowave emission. Thus, radiotelescope surveys allow the distribution if hydrogen across the plane of the milky way and its Doppler shift allows us to determine the speed at which the (H) gas in the galaxy rotates. 2 GLSS P. H. Regan 24

Molecular Gas Clouds (CO p 446) • Typical temperatures of around 20 K (c. f. ISM typical temp ~ 100 K). • Density in such clouds ~ 102 -7 atoms /cm 3 (c. f. sea level earth atmosphere ~3 x 1019 /cm 3). • Gas is mostly molecular hydrogen, H 2…(ISM gas is mostly H-II, i. e. , ionised H 2 mols). • Note that the H 2 molecule does NOT emit the 21 cm line. Thus hard to identify in visible region (use rotational decays)…also need to use tracers with known relative abundances, such as CO, CH, OH and C 3 H 2. Giant Molecular Clouds (GMC) These are very large collections of dust and gas with T~20 K with typical densities of ~100 -300 cm-3. They can stretch for distances of 50 parsecs and contain up to 106 solar masses. Inside the GMCs are more hot and dense cores with dimensions of 0. 05 -1 parsec, T~100 -200 K and densities of 107 -109 /cm 3. 1000 s of GMC are known in our galaxy, mostly in the spiral arms (see later) 2 GLSS P. H. Regan 25

Bok Globules (RJS p 375, CO p 446) Names after Bart Bok, these are dark (cold, dense) regions which are often seen projected against bright nebulae. Bok globules are small, dense clouds, with large visual extinctions (al~10) and low temperatures (~10 K). They are relatively dense (~104 cm-3) and have masses between 1 and 1000 solar masses, with sizes of around 1 parsec. About one quarter of these have young, proto-stars inside. IC-2948 Bok Globules Inside this emission nebula are groups of dark, opaque clouds, i. e. , Bok globules. See http: //www. aao. gov. au/images/general 2 GLSS P. H. Regan 26

Some good web pages for galaxy informantion and figs. n n n n users. erols. com/arendt/Galaxy/mw. html www. whfreeman. com/universe 6 e antwrp. gsfc. nasa. gov/apod/archivepix. ht ml adc. gsf. nasa. gov/mw/mmw_sci. htmlmaps cdsweb. ustrasbg. fr/astroweb/survey. html skyandtelescope. com www. eso. org/outreach/press-rel/pr 2002/pr-17 -02. html zebu. uoregon. edu/~soper/Milky. Way/sah pley. html 2 GLSS P. H. Regan 27

ISM, Composition (RJS p 444) Interstellar Dust Early studies of UV radiation showed spectral features at 220 nm wavelength, corresponding to known transitions from graphite (carbon). Infra-red astronomy then showed that some stars were surrounded by dust shells which heat up and subsequently re-radiate in the infra-red region. Although these spectra are generally continuous, for some stars, an extra continuous peak was superimposed on the usual black body spectrum at wavelengths of approx. 10, 000 nm. This was consistent with significant amounts of silicates (e. g. quartz Si. O 2) in the dust cloud. It has been suggested that C and Si grains are formed in the carbon-rich atmospheres of giant pulsating stars. At expansion, the outer layers of such stars cool and the carbon atoms can stick together to make ‘grains’. When this region heats up again, the increased radiation pressure from the star pushes these out of the star’s atmosphere and into space. 28 2 GLSS P. H. Regan

Interstellar Gas (RJS p 366 ff, CO p 447) The ISM also contains large amounts of gas, which is mostly made up of hydrogen. Depending on the density and temperature of the regions where this hydrogen is, it can exists either in its natural atomic form (HI), its stable molecular form (H 2) or the ionised form of the molecule (HII). In addition to hydrogen, a number of other molecules have been observed in the ISM, such as CO (carbon monoxide), SO 2 (sulphur dioxide), OH (hydroxyl), H 2 O (water), NH 3 (Ammonia), H 2 CO (formaldehyde), H 2 S (hydrogen sulphide) CH 3 CH 2 OH (ethyl alcohol!), HC 11 N (organic? ). These molecules are identified by their emissions which occur in the UV, visible and IR regimes. Usually decays from excited states are by photon with wavelengths in the mm region corresponding from the decay from a rotational state to one with a slightly slower rotation. Such wavelengths can penetrate the earth’s atmosphere and be observed. 2 GLSS P. H. Regan 29
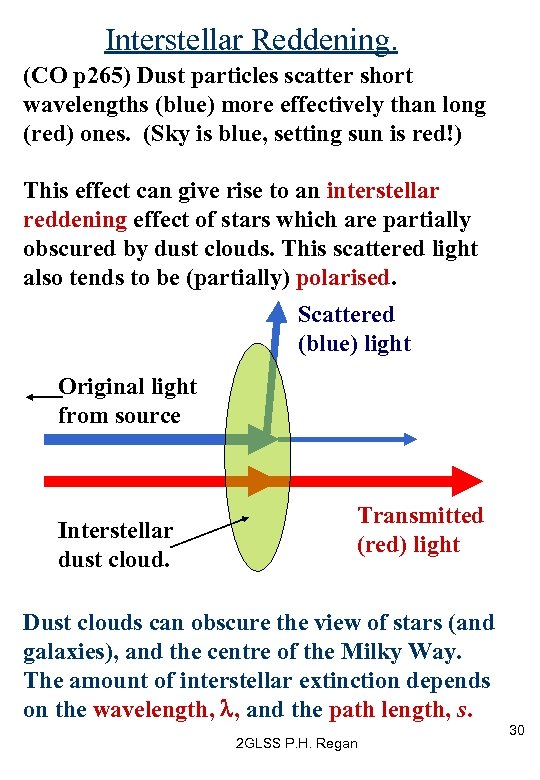
Interstellar Reddening. (CO p 265) Dust particles scatter short wavelengths (blue) more effectively than long (red) ones. (Sky is blue, setting sun is red!) This effect can give rise to an interstellar reddening effect of stars which are partially obscured by dust clouds. This scattered light also tends to be (partially) polarised. Scattered (blue) light Original light from source Interstellar dust cloud. Transmitted (red) light Dust clouds can obscure the view of stars (and galaxies), and the centre of the Milky Way. The amount of interstellar extinction depends on the wavelength, l, and the path length, s. 2 GLSS P. H. Regan 30

(See CO p 265, p 438) Absorption includes the scattering of light and true absorption from e. g. , electrons being to higher energy states in atoms and molecules. It is wavelength dependent. If d. Il is the change in intensity through distance ds, then Opacity is the cross-section for absorbing photons of wavelength, l, per gm of stellar material. 2 GLSS P. H. Regan 31

Spectral Maps of the Galaxy Ref http: //adc. gsfc. nasa. gov/mw/mmw_images. html 2 GLSS P. H. Regan 32

Standard Model of the Universe. • Big Bang ~2 x 1010 years ago, created an expanding universe, now 2 x 1010 ly radius (constant expans. ) • Primordial Abundances: ~80% Hydrogen, ~20% Helium, trace amounts of Li and Be. • After ~105 years, regions condense, gravitational energies leads to heating, nuclear reactions (proton-proton chain), stars form. • H burns to He (p-p chain). For heavy stars, nuclear fusion reactions can burn to form elements all the way up to Iron (Fe, Z=26). • Small stars eject planetary nebula which releases some material into space, but most kept in core (to form white dwarf). • Large stars (>10 Mo) have life cycles of ~107 years followed by cataclysmic supernova. Most of their material is expelled into the ISM. • New stars form in the ISM which are metalsrich ( i. e. , higher metalicities). 2 GLSS P. H. Regan 33
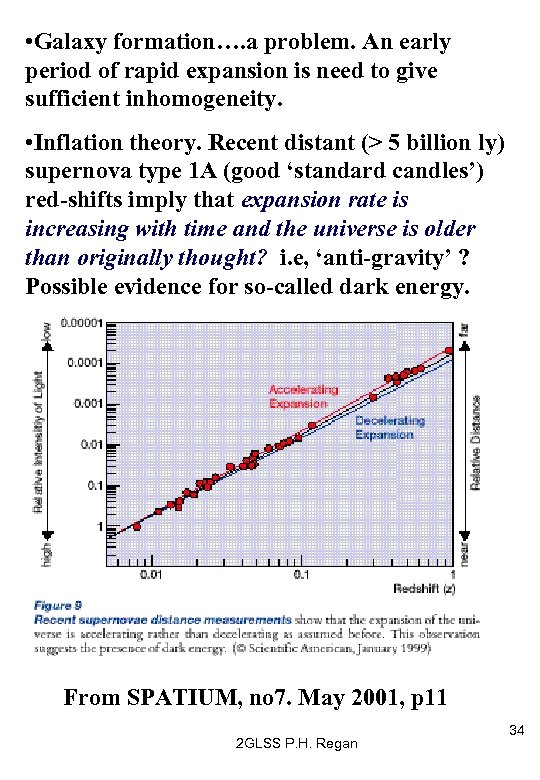
• Galaxy formation…. a problem. An early period of rapid expansion is need to give sufficient inhomogeneity. • Inflation theory. Recent distant (> 5 billion ly) supernova type 1 A (good ‘standard candles’) red-shifts imply that expansion rate is increasing with time and the universe is older than originally thought? i. e, ‘anti-gravity’ ? Possible evidence for so-called dark energy. (see Burrows, Nature 403 (2000) p 727 -733). From SPATIUM, no 7. May 2001, p 11 2 GLSS P. H. Regan 34
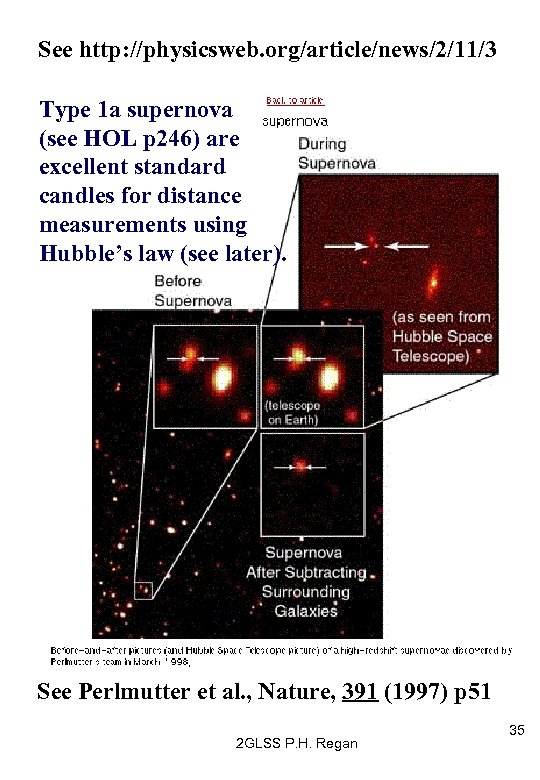
See http: //physicsweb. org/article/news/2/11/3 Type 1 a supernova (see HOL p 246) are excellent standard candles for distance measurements using Hubble’s law (see later). See Perlmutter et al. , Nature, 391 (1997) p 51 2 GLSS P. H. Regan 35

Our Galaxy, The Milky Way (CO, chapter 22 RJS chapter 20) n n n Sun located 8(1)kpc from galactic centre. Orbital period 2. 2 x 108 years, orbital speed of 790, 000 km/h. 50 kpc disk of 600 pc thickness and a central bulge of approx. 3 kpc thick. Total galactic mass of approx 1011 -12 solar masses. 10% of mass attributed to 200 -400 million stars, gas and dust with other possible 90% ‘dark matter’. Supermassive black hole in centre with mass of approx. 3 x 106 solar masses. 2 GLSS P. H. Regan 36

Distribution of Globular Clusters. (RJS p 436) (1917) Before effects of dust were known, Harlow Shapley studied the distribution of globular clusters in space. He calculated their distances using (variable) standard candles known as RRLyrae stars located within these clusters. Shapley found that these clusters were further from the sun that thought and thus the galaxy must be larger than previously believed. Shapley reasoned that these large globular clusters were such large components of the galaxy that they would be unlikely to be distributed to one side. He thus proposed that the centre of the globular cluster distribution coincided with the centre of the galaxy, and thus that the sun was actually quite far from the centre. (Modern value is between 25 -30 Kly). 2 GLSS P. H. Regan 37

http: //www. seds. org/messier/m/m 002. html M 2 cluster (‘Messier object’). First found by Maraldi (1746). Messier (1760) catalogued it as nebula but without individual stars. Hershel (~1780) resolved individual stars within the cluster. Approx. 150, 000 stars and diameter of 140 ly 2 GLSS P. H. Regan 38
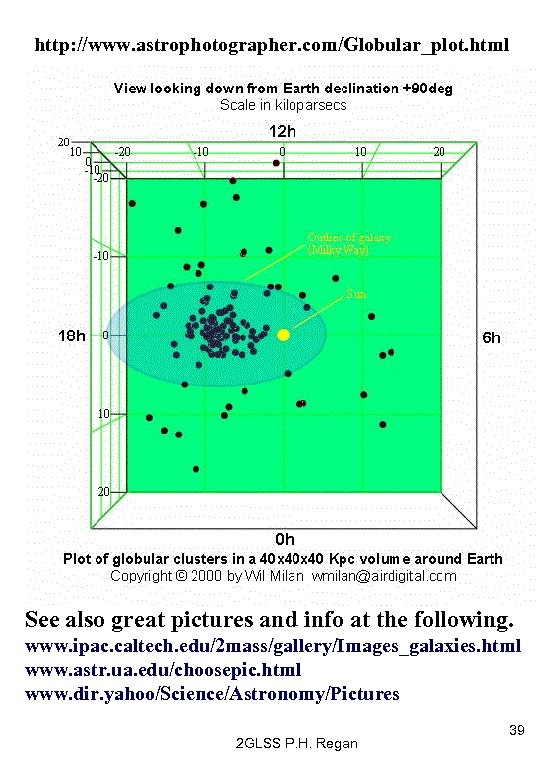
http: //www. astrophotographer. com/Globular_plot. html See also great pictures and info at the following. www. ipac. caltech. edu/2 mass/gallery/Images_galaxies. html www. astr. ua. edu/choosepic. html www. dir. yahoo/Science/Astronomy/Pictures 2 GLSS P. H. Regan 39
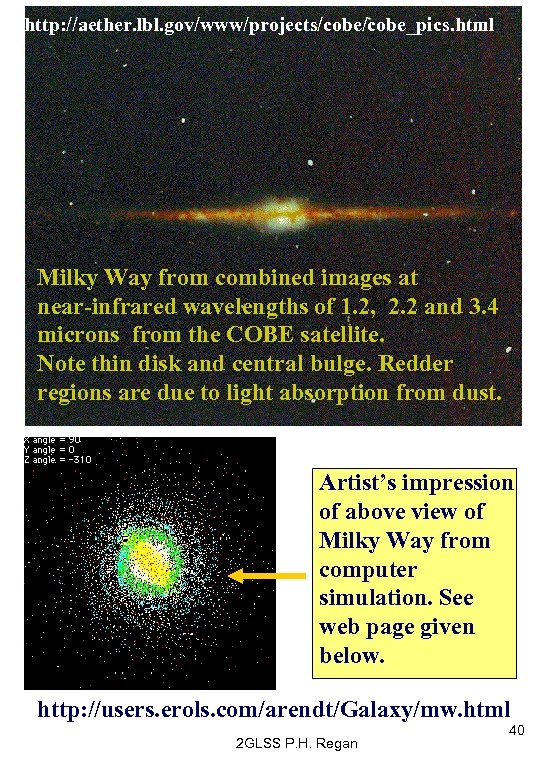
http: //aether. lbl. gov/www/projects/cobe_pics. html Milky Way from combined images at near-infrared wavelengths of 1. 2, 2. 2 and 3. 4 microns from the COBE satellite. Note thin disk and central bulge. Redder regions are due to light absorption from dust. Artist’s impression of above view of Milky Way from computer simulation. See web page given below. http: //users. erols. com/arendt/Galaxy/mw. html 2 GLSS P. H. Regan 40

Details of the Structure of the Milky Way (see CO p 927 ff, RJS p 439, p 457) halo disk nucleus bulge sun ~15 kpc Thin disk is metal-rich, [Fe/H]~0, star formation, lots of young blue stars. Around 325 parsec region of sun. Thick disk, metal-poor [Fe/H]~-0. 5, older stars. Disk thickness increases towards the inner regions of galaxy. Gas/dust in disk absorbs visible light, but 21 cm H-I line ok. Thus, radiotelescopes can map velocity and distribution of H-I gas. Galactic bulge. Spheroidal region near centre of galaxy. Only certain w. lengths observed due to dust. Disc meets the galactic bulge at a radius of approx. 1 kpc. Vertical scale in bulge is around 400 parsecs (along the bulge’s minor axis). Major to minor axis ratio for the bulge is thought to be a ~0. 6. Wide range in metallicity, in the bulge with 1 < [Fe/H] <+1, average ~ +0. 3, i. e. , average Fe to H ratio is about 2 x solar value. i. e. , younger stars dominate here. Bulge mass is ~ 1010 Mo. 2 GLSS P. H. Regan 41

The surface brightness of the bulge, I, in units of Lopc-2 is given by the r 1/4 law, also known as de Vaucloulers profile (1948). Confirmed by COBE results. Re is the reference radius, Ie is the surface brightness at re. Formally, re is defined as the radius at which one half of the bulge’s light is emitted. Baade’s window is a gap in the dust clouds in the bulge which allows the observation of RRLyrae stars (standard candles) beyong the galactic centre. Appears 3. 9 o below and within 550 parsecs of the galactic centre. Galactic B-field: Disk field estimated to be approx 0. 4 n. T (~10 -5 times solar B-field). Deduced from Zeeman-splitting effect on the two states in H-I resposible for the 21 cm line). Also from polarisation of scattered light. 2 GLSS P. H. Regan 42

The Stellar Halo is the region around the disk and bulge. It is made up of a few hundred globular clusters and many high-velocity (‘field’) stars. The globular clusters consist of old, metal-poor stars, with the oldest clusters ([Fe/H] <-0. 8) scattered throughout the halo. Appear to be approx. 1. 6 x 1010 years old ( i. e. as old as the universe, surely not possible. . see RJS p 930 and chaps. 25 and 27) (CO p 930) Two distinct regions of metallicity for globular clusters, Generally, more metal-poor (older) in spherical distribution around galactic centre with more metal-rich (younger) in galactic plane. 2 GLSS P. H. Regan 43
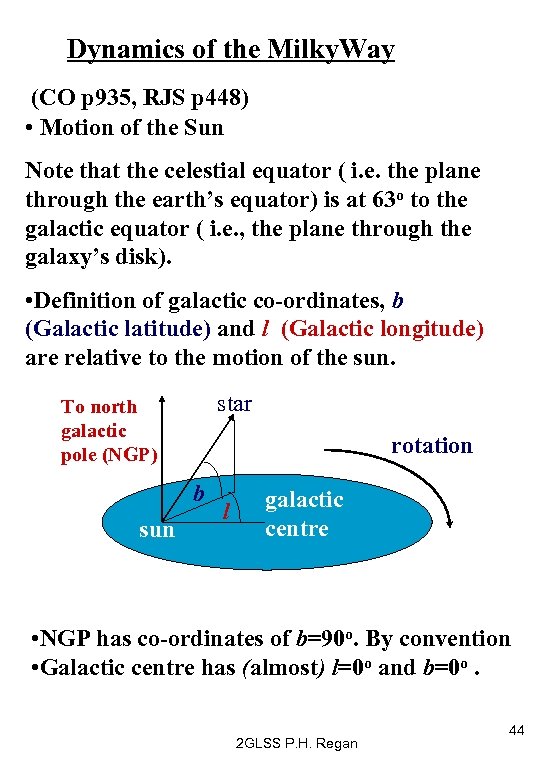
Dynamics of the Milky. Way (CO p 935, RJS p 448) • Motion of the Sun Note that the celestial equator ( i. e. the plane through the earth’s equator) is at 63 o to the galactic equator ( i. e. , the plane through the galaxy’s disk). • Definition of galactic co-ordinates, b (Galactic latitude) and l (Galactic longitude) are relative to the motion of the sun. star To north galactic pole (NGP) rotation b sun l galactic centre • NGP has co-ordinates of b=90 o. By convention • Galactic centre has (almost) l=0 o and b=0 o. 2 GLSS P. H. Regan 44
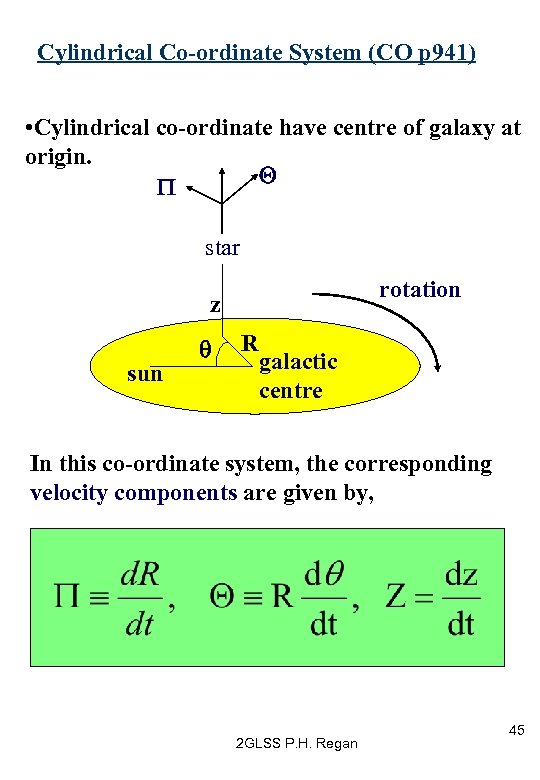
Cylindrical Co-ordinate System (CO p 941) • Cylindrical co-ordinate have centre of galaxy at origin. Q P star rotation z sun q R galactic centre In this co-ordinate system, the corresponding velocity components are given by, 2 GLSS P. H. Regan 45

Local Standard of Rest (LSR) CO p 942) To investigate the motion of the sun and other local stars, we must first define the Local Standard of Rest (LSR). This is defined as a point which is instantaneously centred on the sun and moving in a perfect circular orbits about the galactic centre. Thus, by definition, the velocity components about the LSR must be The velocity of star relative to the LSR is known as the peculiar velocity and is given by 2 GLSS P. H. Regan 46

Motion of Sun in Galaxy (see CO p 945) The LSR has Q 0~220 km/s and a rotational period of about 230 million years. To a good approximation, there is no motion relative to the LSR in the R and z directions, but there is a significant Q effect (see CO p 943). The sun’s peculiar velocity (relative to the LSR) is called the solar motion and has values of: 2 GLSS P. H. Regan 47

Measuring Velocities (CO 107, p 126 -127) Proper motion. Change over time of stellar co-ordinates. Note that need to know distance (only useful for nearby stars). vq vr star r observer Doppler Shift Christian Doppler (1842) found that as the sound waves moved through air, the observed w. length, lobs, is compressed in the forward direction and expanded in the backward direction (compared to a stationary observer) by the expression, 2 GLSS P. H. Regan 48
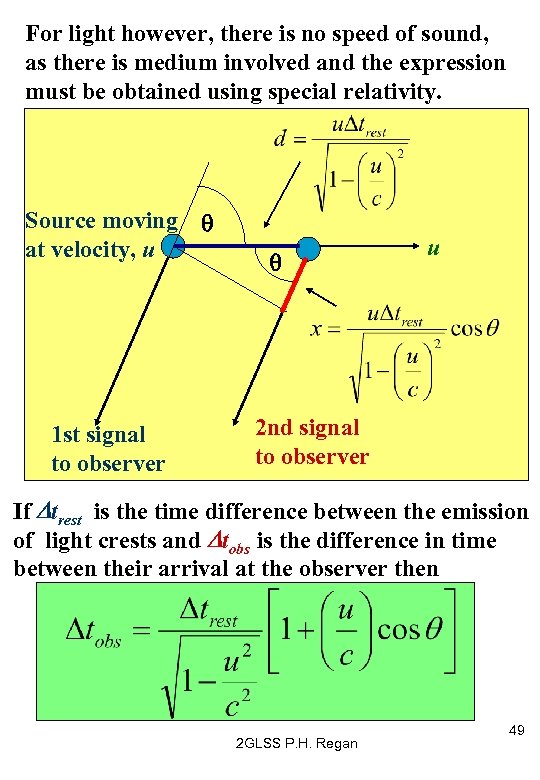
For light however, there is no speed of sound, as there is medium involved and the expression must be obtained using special relativity. 1 st signal to observer q q Source moving at velocity, u u 2 nd signal to observer If Dtrest is the time difference between the emission of light crests and Dtobs is the difference in time between their arrival at the observer then 2 GLSS P. H. Regan 49

Remembering that the frequencies of the light from the source (nrest) and the observed frequency (nobs) are given by The Relativistic Doppler Shift is then given by Note For RADIAL MOTION ONLY v =vel. n = freq 2 GLSS P. H. Regan 50

For objects moving away from the observer, there is a shift down in frequency ( i. e. up in wavelength) towards to RED end of the spectrum ( i. e. lobs>lrest and vr>0). For movement towards the direction of the observer, the shift is to the BLUE (i. e. lobs<lrest and vr<0) Since most astronomical objects are moving away from the earth, a redshift parameter, z, is used to describe the change in observed wavelength (and thus the radial velocity), where 2 GLSS P. H. Regan 51

Galaxy Rotation (CO p 955 -8, RJS p 477) Can use the circular orbits of stars and Newton’s laws for objects far from the galaxy’s interior, equating the centripetal and grav. forces In a spherically symmetric system, the condition for mass conservation is given by (r=density) This predicted density dependence (~1/r 2) is much slower than deduced from the star counts beyond the centre of the galaxy. The density of luminous (i. e. , visible) stars in the stellar halo appears to fall off as (~1/r 3. 5)…. . This has been put forward as an argument that the majority of mass in the galaxy is actually in the form of Dark Matter. 2 GLSS P. H. Regan 52
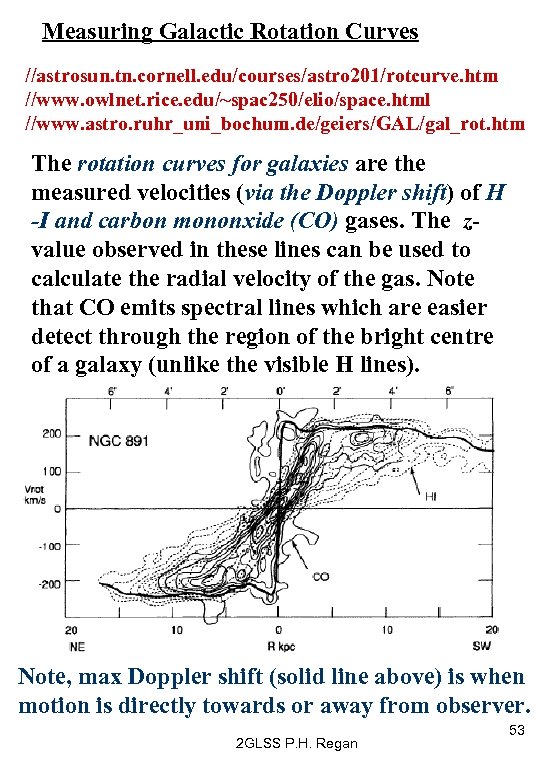
Measuring Galactic Rotation Curves //astrosun. tn. cornell. edu/courses/astro 201/rotcurve. htm //www. owlnet. rice. edu/~spac 250/elio/space. html //www. astro. ruhr_uni_bochum. de/geiers/GAL/gal_rot. htm The rotation curves for galaxies are the measured velocities (via the Doppler shift) of H -I and carbon mononxide (CO) gases. The zvalue observed in these lines can be used to calculate the radial velocity of the gas. Note that CO emits spectral lines which are easier detect through the region of the bright centre of a galaxy (unlike the visible H lines). Note, max Doppler shift (solid line above) is when motion is directly towards or away from observer. 2 GLSS P. H. Regan 53
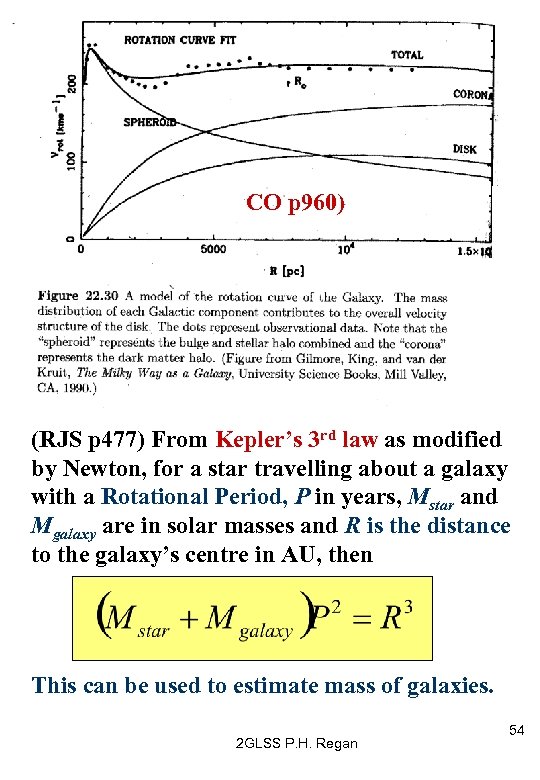
CO p 960) (RJS p 477) From Kepler’s 3 rd law as modified by Newton, for a star travelling about a galaxy with a Rotational Period, P in years, Mstar and Mgalaxy are in solar masses and R is the distance to the galaxy’s centre in AU, then This can be used to estimate mass of galaxies. 2 GLSS P. H. Regan 54
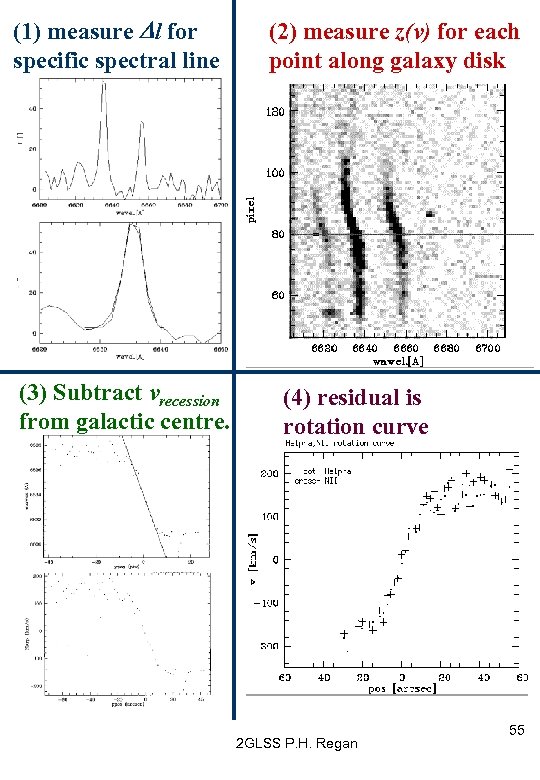
(1) measure Dl for specific spectral line (3) Subtract vrecession from galactic centre. (2) measure z(v) for each point along galaxy disk (4) residual is rotation curve 2 GLSS P. H. Regan 55
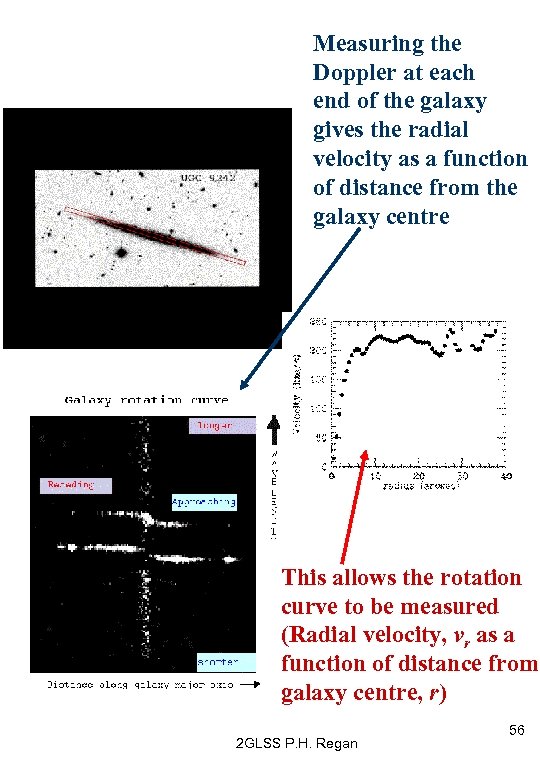
Measuring the Doppler at each end of the galaxy gives the radial velocity as a function of distance from the galaxy centre This allows the rotation curve to be measured (Radial velocity, vr as a function of distance from galaxy centre, r) 2 GLSS P. H. Regan 56
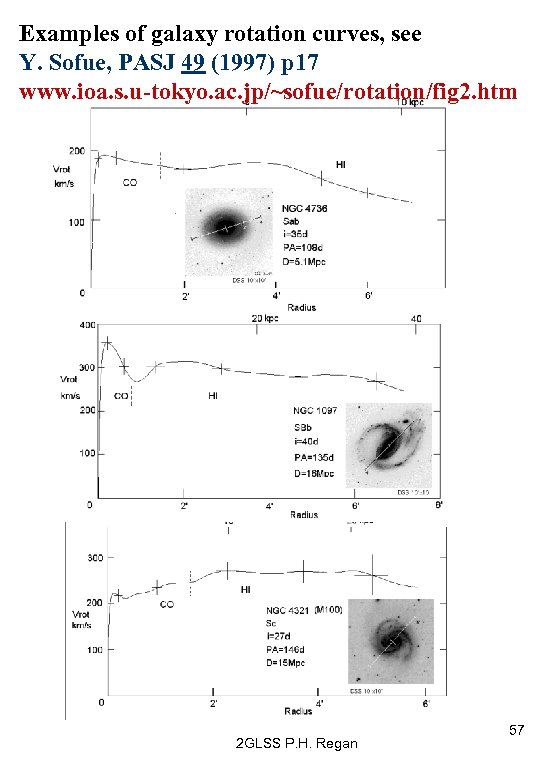
Examples of galaxy rotation curves, see Y. Sofue, PASJ 49 (1997) p 17 www. ioa. s. u-tokyo. ac. jp/~sofue/rotation/fig 2. htm 2 GLSS P. H. Regan 57

The Galaxy (cont). n 21 cm radiowaves from neutral H gas can penetrate the ISM. Large hydrogen clouds can be found in the spiral arms of galaxies (see e. g. , M 31). Looking across the galactic plane, one can observe a series of emission peaks, all slightly shifted with respect to each other. This can be explained by each spiral arm of the Milky Way moving with its own specific rotational velocity (and Doppler shift). It is thus possible to produce maps of the number and orientation of arms in the Milky Way. n Other molecules (as well as H 2) such as OH, CH and CO can also be detected via radio frequency emissions. Giant Molecular Clouds (GMC), which represent stellar formation sites. CO which emits radiation at l=2. 6 mm and regions of this molecule suggest that our galaxy has four major spiral arms (Perscus, Sagitarius, Centaurus and Cygnus). The Sun is situated on a smaller branched arm spiral known as Orion. 2 GLSS P. H. Regan 58
From Astronomy by Zeilikk (John Wiley and Sons) Note, artists impression…not data! 2 GLSS P. H. Regan 59

• There is optical evidence for the spiral structure of the Milky Way, using socalled SPIRAL TRACERS (see RJS p 203). These include the presence of young, (Population I) blue (O and Btype) stars, high-metallicity stars. • Hot, ionised hydrogen (H-II) regions are also associated with stellar formation and might be expected to be found in the spiral arms. • Other spiral tracers include (i) Emission Nebula illuminated by hot O and B stars, (ii) Giant Molecular Clouds (GMCs) and (iii) Supernova Remnants 2 GLSS P. H. Regan 60

Andromeda galaxy (M 31) at various wavelengths See http: //sirtf. caltech. edu/Education/Messier/m 31. html 2 GLSS P. H. Regan 61

Rotation Curve for the Milky Way (dark matter) n n n Optical and radioastronomy seem to indicate that all stars in the galaxy travel at the approx. the same rotational speed. Thus stars closer to the centre complete their orbits faster than the ones at the edge. This results in spiral shapes. But as we know the approx. age of the galaxy and the rate at which the sun rotates around the galactic centre, the Milky Way should be more tightly wound than it is. Failure of Kepler’s third law…more matter in middle maybe ? Dark matter ? Why don’t the arms wind up ? Supernovae may stretch new groups of stars into arms. Also spiral density waves and self-propogating star formation, the ‘ice -skater’ model. Freeman’s Law (see CO p 999, all spirals have ~equal surface brightnesses) 2 GLSS P. H. Regan 62

Supermassive Black Hole ? (CO p 970, HOL p 263) n Our galaxy is probably a ‘barred-spiral’. n The strongest infra-red emission line is found in a region at the centre of the galaxy called Sagittarius A (Sgr. A), which is also a strong source of synchrotron radiation (I. e. a point radio-source, Sgr A*. n From around 1995 onwards, infra-red (2. 2 mm) enabled the velocities of ~90 stars close to to Sgr. A* to be measured. n Implication from Newtonian mechanics, radio -source and x-ray flares is a supermassive black hole with approx 2. 6 x 106 solar masses at centre of Milky Way (see Ghez et al, . Nature 407 (2000) p 349, see also http: //physicsweb. org/article/news/6/10/12 n Distance of galactic centre is approx 26, 000 ly from earth 63 2 GLSS P. H. Regan
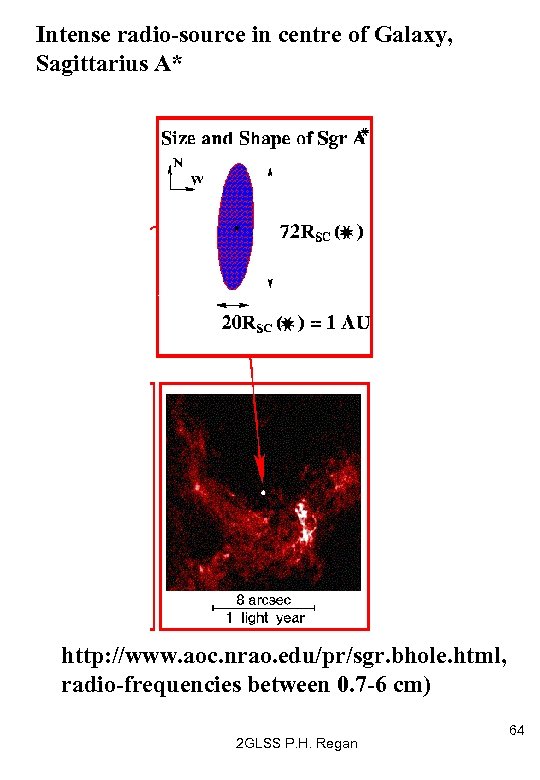
Intense radio-source in centre of Galaxy, Sagittarius A* http: //www. aoc. nrao. edu/pr/sgr. bhole. html, radio-frequencies between 0. 7 -6 cm) 2 GLSS P. H. Regan 64
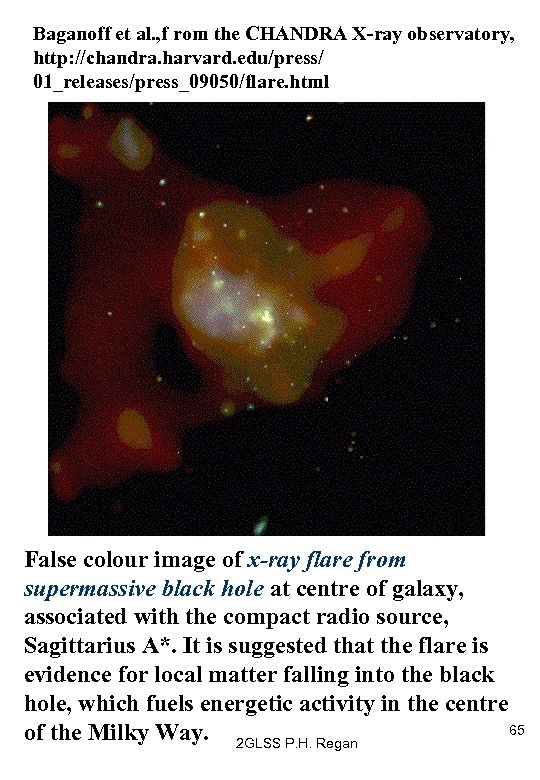
Baganoff et al. , f rom the CHANDRA X-ray observatory, http: //chandra. harvard. edu/press/ 01_releases/press_09050/flare. html False colour image of x-ray flare from supermassive black hole at centre of galaxy, associated with the compact radio source, Sagittarius A*. It is suggested that the flare is evidence for local matter falling into the black hole, which fuels energetic activity in the centre 65 of the Milky Way. 2 GLSS P. H. Regan

Galaxies in General: A Brief History n Messier (1730 -1817) recorded 103 fuzzy objects (nebulae) in the Messier catalogue (M@). n Dreyer (1852 -1926) published the New General Catalogue (NGC) of almost 8, 000 nebulae (NGC@), but not known at this point whether they were galactic or extragalactic phenomena. n 1923, Hubble detected Cephied variables in M 31 (Andromeda galaxy, NGC 224), showed extra-galactic nature. 2 GLSS P. H. Regan 66

Morphology of Galaxies: Galaxy Types. (RJS p 468, CO p 990, HOL p 257) Galaxies are broadly classified into three types by a scheme known as the Hubble Sequence. This divides galaxies into (i)Ellipticals (E), (ii) Spirals (S) & (iii) Irregulars (Ir). The spirals are further subdivided into two sequences, namely (iia) Normal Spirals (S or SA) and (iib) Barred Spirals (SB). There also a class of galaxies which are transitional between ellipticals and spirals, known as Lenticulars, which can be either ‘normal’ (SO) or barred (SBO). These arranged by Hubble’s Tuning Fork Diagram. normal spirals ellipticals barred spirals Hubble thought (wrongly!) this was an evolution of type 2 GLSS P. H. Regan 67

(RJS p 468, CO p 997, HOL p 258) • ELLIPTICAL (E) galaxies are ellipsoidal in shape and contain no spiral arms. They contain little interstellar dust and gas and are found mostly in rich clusters of galaxies. Elliptical galaxies typically appear yellow-red in colour. There are few blue, young, recycling stars (in contrast to spiral galaxies, whose spiral arms are full of young stars and appear quite blue). Supergiant Ellipticals have radii up to 106 pc. http: //www. antwrp. gsfc. nasa. gov/apod/lib/ellipticals M 87 elliptical galaxy NGC 4881 Giant Elliptical galaxy) 2 GLSS P. H. Regan 68

• SPIRAL (Sa, Sb, etc. ) galaxies consist of a large, dominant central bulge and tightly wound spiral arms. Star formation in the bulge region is thought to have taken place long ago and thus light from this region is blue-deficient (since massive, blue stars are relatively short lived), but rather reddish (from red-giants). This contrasts with the spiral arms, where new, blue, stars are formed. Spirals have (i) a flat disk, which usually contains a lot of interstellar matter and (ii) hot, massive, young (blue. O and B type) star clusters, which are usually arranged in spiral patterns structures. Some spirals have a large ‘bar’ through their central region and are known as ‘barred spirals’. (The milky way is thought to be a barred-spiral galaxy). Hubble subdivided spiral galaxies into Sa, Sab, Sbc, Sc and Sba, Sbab, SBbc and SBc. Those galaxies with the largest bulgeto-disk luminosity ratios, the most tightly wound spiral arms and the smoothest distribution of stars are classified as Sa or Sba. Conversely, Sc and SBc galaxies have loosely wound arms etc. 2 GLSS P. H. Regan 69

http: //www. antwrp. gsfc. nasa. gov/apod/lib/spirals Andromeda galaxy (M 31) closest galaxy ~ 2 million ly companion galaxy (NGC 5195) Whirlpool Galaxy (M 51) 2 GLSS P. H. Regan 70

The ‘Sombrero’sprial galaxy (M 104), clearly showing the dust in the disk, the central bulge and globular clusters within the stellar halo. See http: //www. noao. edu/image_gallery 2 GLSS P. H. Regan 71
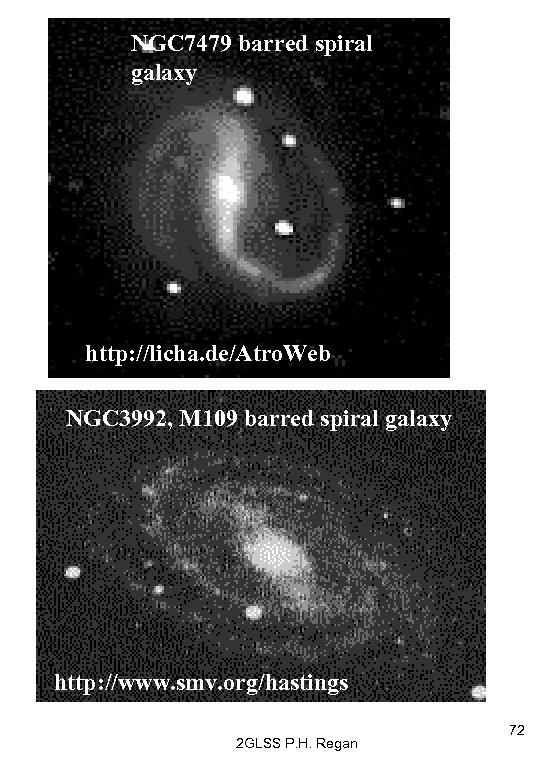
NGC 7479 barred spiral galaxy http: //licha. de/Atro. Web NGC 3992, M 109 barred spiral galaxy http: //www. smv. org/hastings 2 GLSS P. H. Regan 72

• LENTICULAR (SO, SBO) galaxies consist of flat disk with a central bulge but do not show any spiral arms (unlike spiral galaxies). Depending on the orientation relative to the earth, such galaxies can appear circular (if seen face on), elliptical, or thin and elongated. NGC 4546 (SB 0) Lenticular galaxy from http: //www. sunspot. noao. edu/sunspot/pr/tree NGC 3384 (SO) lenticular galaxy 2 GLSS P. H. Regan 73

• IRREGULAR (Irr) galaxies have a chaotic appearance which does not resemble either spiral or elliptical galaxies. Many of the smallest galaxies are irregular (including the Magellanic clouds which accompany the Milky Way). M 82 Irregular galaxy http: //www. sunspot. noao. edu/sunspor/pr/tree 2 GLSS P. H. Regan 74

Size of Galaxies (CO p 998) By mapping contours of constant brightness, (ISOPHOTES), one can infer the matter radius of galaxies. BUT, galaxies do not have sharp edges, thus radii are not well defined. The effective radius (re ) , is defined as the radius within which half of the galaxies light is emitted. For the bulges of spirals and large ellipticals, this looks like (from equn, on page 42) where m( r) is the surface brightness in units of magnitude/arcsec 2 and me is the surface brightness at the effective radius, re. (Note, that galaxial disks are usually modelled with an exponential , rather than r 1/4 decay). 2 GLSS P. H. Regan 75

The Tully-Fisher Relation (CO p 1001, RJS p 476) It is reasonable to assume that the greater the mass in a given galaxy, the larger its luminosity. It then follows, the greater the mass, the larger the gravitational force at each point in the galaxy would be. Since it is the size of this gravitation force which determines the rotation velocity of the galaxy (see equn. P 52), there will be a relationship between the rotational velocity and luminosity of galaxies. The rotational velocity of galaxy can be deduced from the Doppler broadening of the 21 cm line. This will be both red and blue shifted. A value for the absolute luminosity for the galaxy can be estimated and compared with the observed brightness. The inverse square law of light can be used to make an estimate of galaxy’s distance. The relationship between the luminosity and rotational velocity of galaxies is known as the Tully-Fisher relation (1977). 2 GLSS P. H. Regan 76
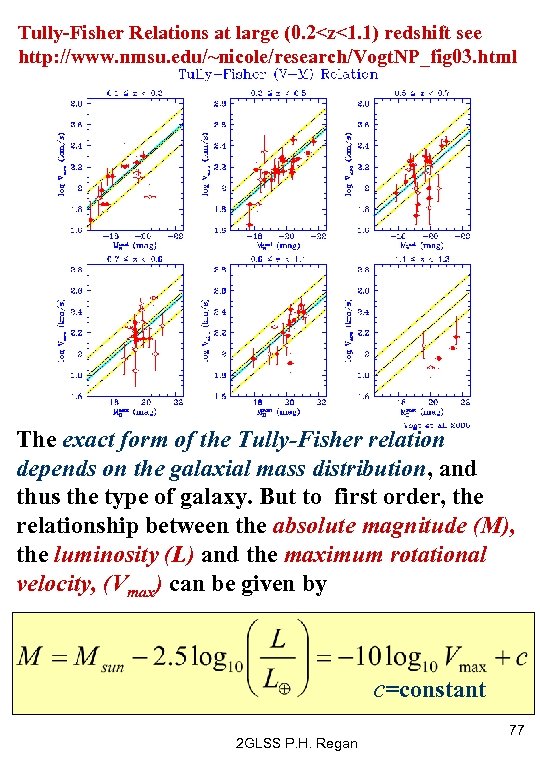
Tully-Fisher Relations at large (0. 2<z<1. 1) redshift see http: //www. nmsu. edu/~nicole/research/Vogt. NP_fig 03. html The exact form of the Tully-Fisher relation depends on the galaxial mass distribution, and thus the type of galaxy. But to first order, the relationship between the absolute magnitude (M), the luminosity (L) and the maximum rotational velocity, (Vmax) can be given by c=constant 2 GLSS P. H. Regan 77

Stellar Distributions and Metallicities • H-I gas in our galaxy is distributed in spiral arms, connected to the bulge. • Most young (blue) stars are in these arms, i. e. , these are regions of on-going star formation. • Since stars form from gas clouds, and massive (blue) stars form and die relatively quickly, one expects (all) massive, main sequence stars to be found in the spiral arms. • Older stars are red in colour (further down main sequence, red giants. . ) These are found in the disk, not in the spiral arms. Red stars can are also found in the bulge and halo. • Observations indicate that the metallicity of a galaxy correlates with its absolute magnitude and thus luminosity. This implies that chemical enrichment is more efficient in luminous, massive galaxies. Possibly due to them having more massive stars in which subsequently go to type II supernova ? 2 GLSS P. H. Regan 78
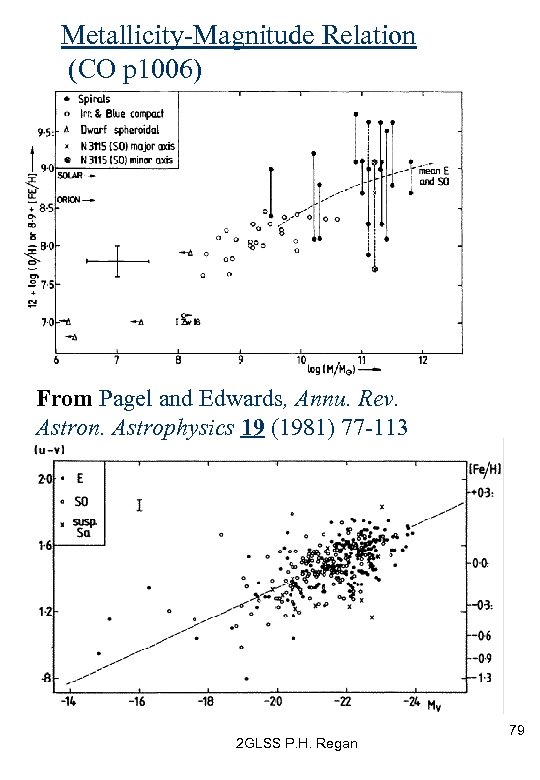
Metallicity-Magnitude Relation (CO p 1006) From Pagel and Edwards, Annu. Rev. Astron. Astrophysics 19 (1981) 77 -113 2 GLSS P. H. Regan 79

Galaxy Clusters and Colliding Galaxies (CO p 1053 -10073, p 1119 ff) Most galaxies belong to clusters, which can contain 1000 s of individual galaxies. Groups of galaxies usually have less than 50 members, with clusters containing between 50 and several thousand individual galaxies. Galaxy clusters are classified as either regular (spherical and centrally condensed) or irregular. The Milky Way belongs to the LOCAL GROUP, which consists of approx. 30 galaxies, including the Andromeda Galaxy (M 31), M 32, M 33, M 110 and the Small and Large Magellanic Clouds (LMC, SMC). The Milky Way and Andromeda galaxies are by far the largest and most dominant members of the local group. There also around 20 small groups of galaxies within approx 14 Mpc of the local group, including the Maffei-1, the South Polar or ‘Sculptor’, the M 81 and the M 83 groups. Out group of galaxies is in gravitational interaction with these galaxy groups. 2 GLSS P. H. Regan 80
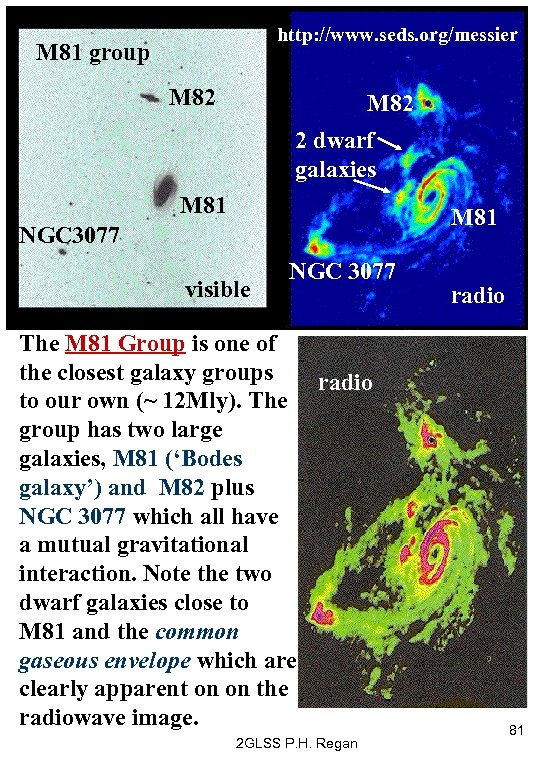
http: //www. seds. org/messier M 81 group M 82 2 dwarf galaxies M 81 NGC 3077 visible NGC 3077 The M 81 Group is one of the closest galaxy groups radio to our own (~ 12 Mly). The group has two large galaxies, M 81 (‘Bodes galaxy’) and M 82 plus NGC 3077 which all have a mutual gravitational interaction. Note the two dwarf galaxies close to M 81 and the common gaseous envelope which are clearly apparent on on the radiowave image. 2 GLSS P. H. Regan radio 81
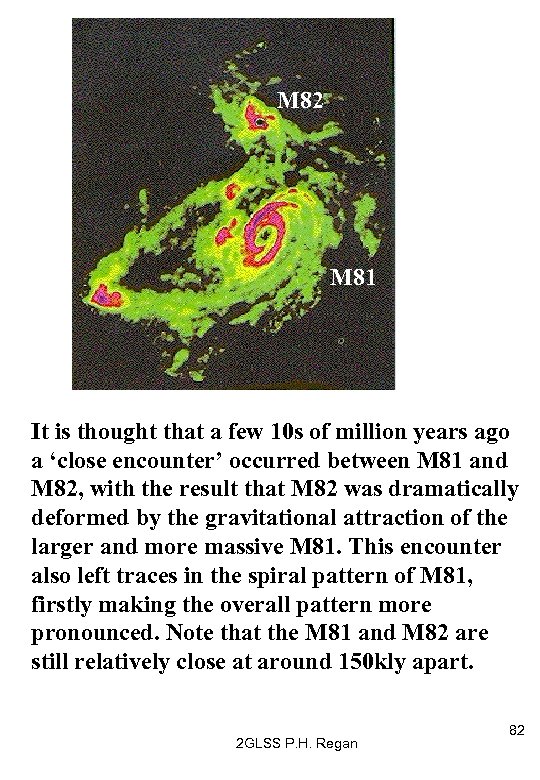
M 82 M 81 It is thought that a few 10 s of million years ago a ‘close encounter’ occurred between M 81 and M 82, with the result that M 82 was dramatically deformed by the gravitational attraction of the larger and more massive M 81. This encounter also left traces in the spiral pattern of M 81, firstly making the overall pattern more pronounced. Note that the M 81 and M 82 are still relatively close at around 150 kly apart. 2 GLSS P. H. Regan 82

• Gravitational attraction between nearby galaxies means they can interact and even collide with each other. • Colliding galaxies does not imply colliding stars (size between individual stars too large). • There can be dynamical friction between galaxies due to the gravity (see CO p 1055). This dynamical friction force (‘drag’), fd, can be estimated assuming fd ~ (r / v 2) where v is the relative speed of the colliding galaxies and r is the density of the colliding material. • Energy will also be converted from potential and self-energy into kinetic energy of individually scattered stars. • Kinetic energy from the galaxies’ motions of can be transferred into internal KE of the gravitationally interacting galaxies. • Gravitationally bound galaxies willeventually merge (e. g. Milky Way and LMC & SMC, also some evidence double nucleus in Andromeda, M 31 galaxy). • The mergers and tidal interactions ‘tidal stripping’ between colliding galaxies may be responsible for matter transfer and creating new active star-forming regions. 83 2 GLSS P. H. Regan

CO p 1066 2 GLSS P. H. Regan 84

2 GLSS P. H. Regan 85

Calculating Galaxy Collisions (CO p 1088) Realistic ‘N-body’ computer simulations can be carried out using Newton’s gravitational equations. Such calculations suggest that many large elliptical galaxies are actually the result of mergers between two spiral galaxies. It is thus thought that over time, spiral galaxies are destroyed by mergers, resulting in the creation of very large elliptical galaxies. Evidence for this includes • Computer based N-body simulations • The observation that elliptical galaxies appear to dominate in the more dense, centres of galaxy clusters • Observations also suggest that the more distant (and thus younger) galaxies appear to have (had? ) a greater fraction of spiral galaxies compared to ellipticals. 2 GLSS P. H. Regan 86
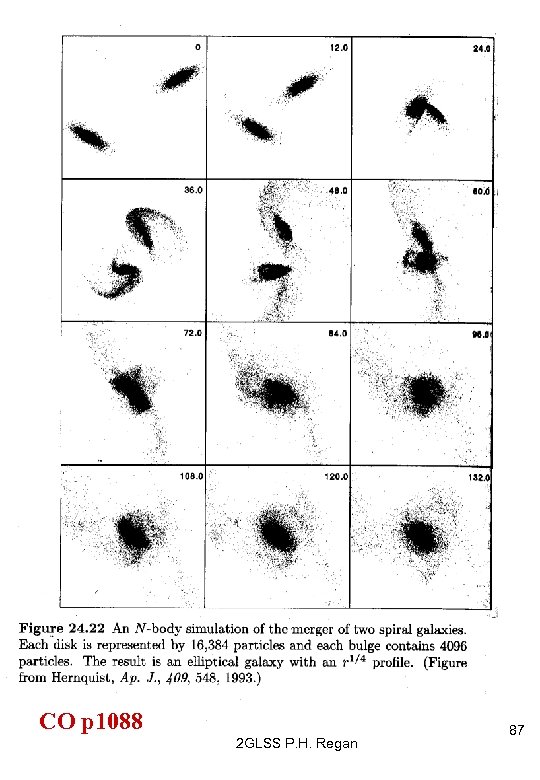
CO p 1088 2 GLSS P. H. Regan 87

In hydrotstatic equilibrium, from the VIRIAL THEOREM (CO p 56) the Total (E), Potential (U) and Kinetic (K) energies of a galaxies are related by the expression 2 K= -U = -2 E For a head-on galaxy collision, we can use the impulse approximation (CO p 1061) to assume the encounter between the galaxies occurs so quickly that the individual stars do not have time to move much from their positions. The gravitational potential energy, U, of the galaxy is virtually unaltered by the collision. If a galaxy increases its internal kinetic energy, from K to K+DK as a result of the gravitational ‘work’ each galaxy has done on the other one, the total energy will also increase from K to K+DK, but the potential energy, U remains unchanged (=K). The galaxy would thus no longer be in hydrostatic equilibrium. To regain equilibrium, the extra 2 DK of kinetic energy obtained just after collision, must be ‘lost’. One way this can be done is for this excess energy to be converted in to increased (i. e. , less negative) gravitational potential energy, by expansion. 2 GLSS P. H. Regan 88

Colliding Galaxies http: //www. seds. org/hst/Cartwheel. html The Cartwheel galaxy (approx 500 Mly away), is an example of a ‘ring galaxy’ (see CO p 1062) which followed from a nearly head-on collision between galaxies. This figure, from the Hubble Space Telescope, shows the effect of a collision by an intruder galaxy (it is not clear which one of the two objects to the right), which smashed through the core of the host galaxy. Note blue, new stars in the ring. The ring is expanding at approx, 90 km/s. 2 GLSS P. H. Regan 89

Sleeping Beauty Galaxy(M 64) http: //antwrp. gsfc. nasa. gov/apod There is a central region where the stars rotate in a different direction to the dust and gas. This effect is thought to be result of collision between a large and small galaxy which has yet to equilibrate out. 2 GLSS P. H. Regan 90

http: //www. noao. edu/image_gallery/html/im 0011. html Interacting galaxies Arp 273 ‘Interacting Galaxies, Arp 273’ distance approx 200 Mly, false colour image from the Anglo-Australian telescope. Note the strong tidal distortion of the larger of the two galaxies and the notable ‘extra’ red nucleus in the smaller, side on galaxy in the botton right of the picture. The lower galaxy has a very active nucleus (see later). 2 GLSS P. H. Regan 91

Superclusters A supercluster is a group of galaxy clusters which appear to be associated (gravitationally) with each other. Unfortunately, this information is not usually known for most galaxy clusters and thus definitions of members of superclusters are made on the basis of how far different galaxy clusters are separated from each other. This definition has some problems, as the distances between galaxies is much more difficult to determine that the distance to them (since we can use the doppler shift to give us more accurate measures of the distance perpendicular to the radial direction, than the radial direction specifically. ) 2 GLSS P. H. Regan 92

Perseus galaxy cluster, see http: //antwrp. gasfc. nasa. gov/apod The Perseus cluster of galaxies, approx. 300 Mly. This is part of the Pisces-Perseus supercluster. Note that the confinement of gas in the large galaxial gravitational field (purple in figure). This extra gravity’ which ROSAT is sufficient to False colour hold the gas in x-ray image place, has been proposed as further potential evidence for Abell 426 Dark Matter 2 GLSS P. H. Regan 93

The Coma cluster contains >1, 000 galaxies, is around 6 Mpc across and lies ~360 Mly away. Centre of galaxy is hot (T~100 x 106 K) gas cloud (see X-ray image) held in by gravity. Coma cluster, see http: //www. astra. au. edu/gifimages/coma. html visible X ray http: //chandra. harvard. edu/x-ray_sources/coma 2 GLSS P. H. Regan 94
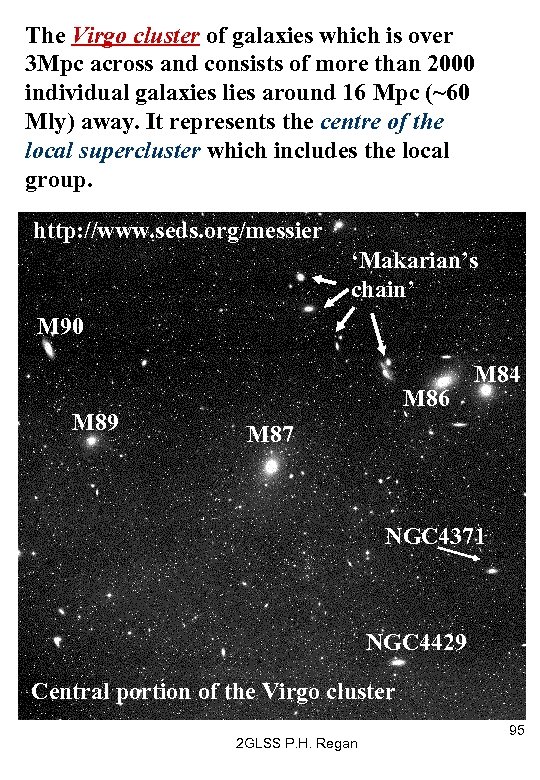
The Virgo cluster of galaxies which is over 3 Mpc across and consists of more than 2000 individual galaxies lies around 16 Mpc (~60 Mly) away. It represents the centre of the local supercluster which includes the local group. http: //www. seds. org/messier ‘Makarian’s chain’ M 90 M 89 M 86 M 84 M 87 NGC 4371 NGC 4429 Central portion of the Virgo cluster 2 GLSS P. H. Regan 95

Expansion of the Universe, Hubble’s Law (CO p 1110) Using luminosity of Cephied variable stars, Edwin Hubble plotted the recessional velocity of such standard candles in extra-galactic objects against their induced distance (deduced using the inverse square law of light). The resulting (nearly? ) linear relationship is known as Hubble’s Law, which has the form, Where V is the recessional velocity and r is the distance from the earth. H is known as the Hubble constant. 2 GLSS P. H. Regan 96
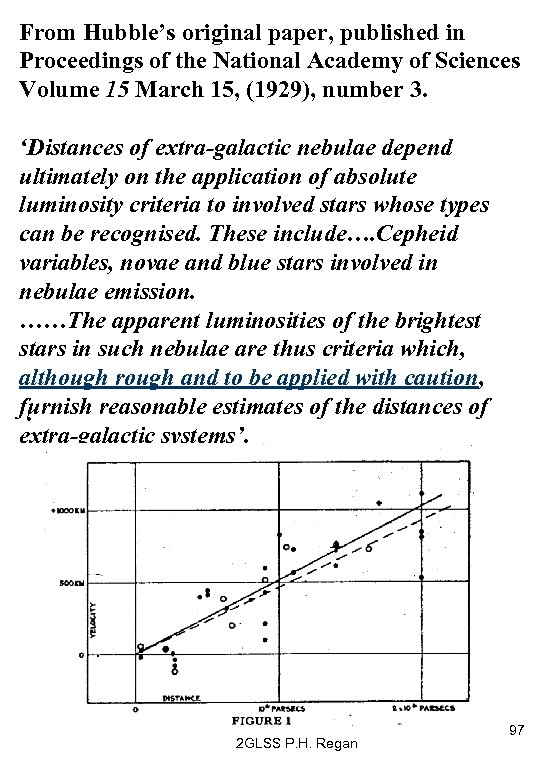
From Hubble’s original paper, published in Proceedings of the National Academy of Sciences Volume 15 March 15, (1929), number 3. ‘Distances of extra-galactic nebulae depend ultimately on the application of absolute luminosity criteria to involved stars whose types can be recognised. These include…. Cepheid variables, novae and blue stars involved in nebulae emission. ……The apparent luminosities of the brightest stars in such nebulae are thus criteria which, although rough and to be applied with caution, furnish reasonable estimates of the distances of ‘ extra-galactic systems’. 2 GLSS P. H. Regan 97

Value of the Hubble Constant, Scale Factors and Hubble Time Hubble’s orginal value for H=530 kms-1 Mpc-1. But subsequent measurements showed that he underestimated the distances involved as what he thought were the brightest stars were actually groups of stars. The value of H appears to have varied over time, thus while it is still a constant of proportionality between V and r, H=H(t). By convention, we the present day value of the Hubble constant is given the symbol, H 0. There is still much debate and measurement on the value of the Hubble constant. Currently, it is standard to define constant using the dimensionless quantity, h, and h has a value between 0. 5 and 0. 8. 2 GLSS P. H. Regan 98

Hubble’s law implies a universal expansion. In this context, the recessional velocity (due to the expansion of space) is distinct from the peculiar velocity (which is due to the motion through space). i. e v = Hod + vpec The recessional velocity arises because space itself is expanding, this is the realm of COSMOLOGY. The cosmological redshift needs to take into account the curvature of space-time (beyond the scope of this course). However, it is common practice to use the redshift equation to obtain the effective radial velocity. Thus, by measuring redshift, the distance can be determined. H 0 is poorly known, use H 0=75(20)kms-1 Mpc-1 (h=0. 75(0. 2)) 2 GLSS P. H. Regan 99
4dfe30bc42f2a1988377078dd2be879d.ppt