SYCS 165 SCIENTIFIC COMPUTING FOR ENGINEERS Ronald J

SYCS 165 SCIENTIFIC COMPUTING FOR ENGINEERS Ronald J. Leach 1

From the Catalog • Introduces programming and use of digital computers. • Programming includes general problemsolving and the systematic development of algorithms • Use includes the coding of programs and practical experience in operating computers and peripheral equipment. 2

Purpose of course • Educate STEM students in the use of three types of software to solve appropriate problems in their major fields: – Spreadsheets – Symbolic computation using computer algebra systems – Numerical computation using standard modern computer languages, primarily C. 3

Why do this? • A new paradigm – data driven science. • Data modeling, analysis, and simulation are becoming increasingly important in STEM. 4

Why three types of software? • There are different types of applications. • There are differences in resources. • There are differences in what you have to interface with. 5

Excel spreadsheets 6

Why spreadsheets? • Spreadsheets are readily available. • They have surprising functionality. • The Excel spreadsheet software may be free to students at Howard University due to the special Howard-Microsoft connection. 7

Other spreadsheets • Open Office – available for Apple, Windows, and Linux computers – free download from Open. Office. org. – The spreadsheet is Calc • Numbers – available for Apple computers –not usually free. 8

Excel capabilities • Many functions are available for – Statistical computations – Graphing – Arrays – Matrices – etc 9

Functions – a glorified calculator • ABS Returns the absolute value of a number • ACOS Returns the arccosine of a number • ACOSH Returns the inverse hyperbolic cosine of a number • ASIN Returns the arcsine of a number • ASINH Returns the inverse hyperbolic sine of a number • ATAN Returns the arctangent of a number • ATAN 2 Returns the arctangent from x- and y-coordinates • ATANH Returns the inverse hyperbolic tangent of a number 10

• CEILING Rounds a number to the nearest integer or to the nearest multiple of significance • COMBIN Returns the number of combinations for a given number of objects • COS Returns the cosine of a number • COSH Returns the hyperbolic cosine of a number • DEGREES Converts radians to degrees • EVEN Rounds a number up to the nearest even integer • EXP Returns e raised to the power of a given number 11

• • FACT Returns the factorial of a number FACTDOUBLE Returns the double factorial of a number FLOOR Rounds a number down, toward zero GCD Returns the greatest common divisor INT Rounds a number down to the nearest integer LCM Returns the least common multiple LN Returns the natural logarithm of a number LOG Returns the logarithm of a number to a specified base • LOG 10 Returns the base-10 logarithm of a number 12

• ODD Rounds a number up to the nearest odd integer • PI Returns the value of pi • POWER Returns the result of a number raised to a power • PRODUCT Multiplies its arguments • QUOTIENT Returns the integer portion of a division • RADIANS Converts degrees to radians • ROMAN Converts an arabic numeral to roman, as text • ROUND Rounds a number to a specified number of digits • ROUNDDOWN Rounds a number down, toward zero • ROUNDUP Rounds a number up, away from zero 13

• • SIGN Returns the sign of a number SIN Returns the sine of the given angle SINH Returns the hyperbolic sine of a number SQRT Returns a positive square root SQRTP Returns the square root of (number * pi) TAN Returns the tangent of a number TANH Returns the hyperbolic tangent of a number TRUNC Truncates a number to an integer 14

Some Array and Matrix Functions • • MDETERM Returns the matrix determinant of an array MINVERSE Returns the matrix inverse of an array MMULT Returns the matrix product of two arrays SUMX 2 MY 2 Returns the sum of the difference of squares of corresponding values in two arrays • SUMX 2 PY 2 Returns the sum of squares of corresponding values in two arrays • SUMXMY 2 Returns the sum of squares of differences of corresponding values in two arrays 15

Some Statistical Functions • • • AVERAGE Returns the average of its arguments DEVSQ Returns the sum of squares of deviations LINEST Returns the parameters of a linear trend LOGEST Returns the parameters of an exponential trend MEDIAN Returns the median of the given numbers MODE Returns the most common value in a data set STDEV Estimates standard deviation based on a sample TDIST Returns the Student's t-distribution … … 16

Functions in Excel • Easy to create in the Visual Basic editor • Standard syntax Function Fcn_Name (arg) Fcn_Name = xxx End Function 17

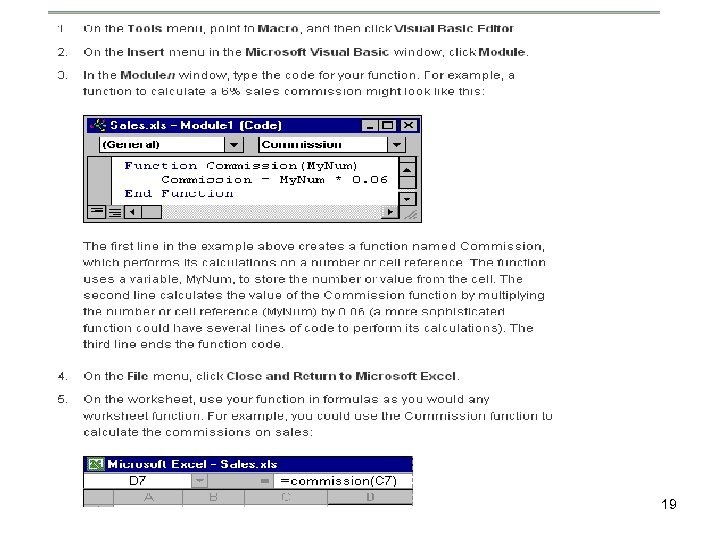
User-defined Functions in Excel • Easy to create in the Visual Basic editor • Standard syntax – reserved words Function Fcn_Name (arg) Fcn_Name = xxx End Function 18

19

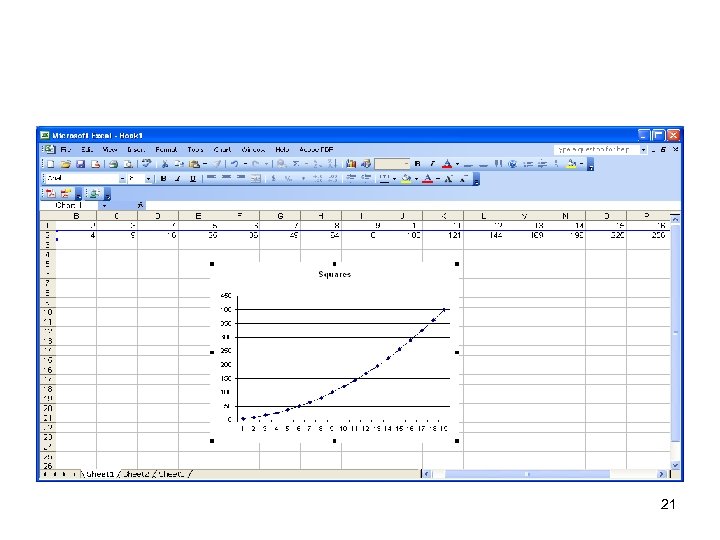
Example Function Square_It(num) Square_It = num * num End Function (Create in VB Macro editor – use the Tools menu) 20

21

Numerical Computations 22

Numerical computation • Standard technique for many complex problems • Many well-established libraries of subprograms • Works well on many classes of supercomputers – Most numerical approximation is applied linear algebra 23

An old Cray vector supercomputer 24

A lot of hand craftsmanship • Wires had to be cut by hand to make sure there were no timing delays or bottlenecks • The speed of light was too slow to have several of these older machines act in tandem. 25

Alliant FX-8 26

Supercomputers • Vector computers could do vector operations (+, -) in a single clock cycle for long vectors 256 or more entries. • Parallel computers could do computations in parallel (think dual-core, but much larger) • The good scientific developers had the target computer’s architecture in mind when developing algorithms and programs 27

A cheaper idea- clusters • Originally, place multiple CPUs in racks, with an operating system to control communication of data and instructions. • Now, place boards with many processors in racks with an operating system to control communication of data and instructions. 28

Many types of clusters • Linux • Windows • Mac 29

Even “cheap” machines are expensive • To buy • To operate – utilities • To program 30

Good quality numerical software • Extensive libraries geared to the particular machine’s architecture. • Nearly all the most useful numerical libraries are written in FORTRAN or C. • Often interface with other languages. 31

• We won’t be using supercomputers or clusters as a basic part of this course. – Exception – some students will do some of their C programming on a cluster, depending on the situation and the needs of their major. • Personal computers are sufficient for an introductory course 32

Computer Algebra Systems 33

Why three types of software? • Computer algebra systems can: – Create exact answers to problems – Produce infinite-precision arithmetic (a better term is “unlimited-precision”) – Many well-tested routines – Perform mathematical calculation in fields such as algebra and calculus much better than humans 34

What about computer algebra systems? • Run on many computers, even some parallel computers and clusters • Not much gain by running on vector machines 35

TI Explorer 2 – a “Lisp Machine” 36

Computer algebra systems • Many of the older ones were written in Lisp (a language often used for AI) – Macsyma – Maxima – Mu. Math – Derive • Some use C (Maple) • Hard to tell for Mathematica, Matlab 37

One unfortunate flaw of CAS • They run out of room! • The CAS will generate lists (in Lisp, C, or whatever language) as necessary. • Sometimes these lists stay in memory even after they are no longer needed. • This means that memory can be exhausted. 38

Types of arithmetic • • • Integer Real (or floating point) Extended precision (double precision) Complex Other? 39

Integer arithmetic • Often limited by the size of a computer “word” • Integers can be too big or small – Largest unsigned integer in a 32 -bit machine is 232 – 1 – Largest positive integer in a 32 -bit machine is 231 – Smallest unsigned integer in a 32 -bit machine is often - 231 40

41

Arithmetic with decimals Floating point arithmetic: • Has largest and smallest numbers. • Has positive number that is closest to 0. • Has negative number that is closest to 0. • Has truncation errors (3. 14 is not 3. 14159) • Has round-off errors (3. 14 * 3. 14 is 9. 8596) 42

Arithmetic with decimals, cont. Fixed point arithmetic • Usually two decimal places • Round-off can be severe – Who stole my bank interest example • No problem with smallest positive number 43

CAS • Can have “infinite precision” or, at least, “unlimited precision” • The trade-off is that arithmetic takes much longer and requires more space 44

For next class • Download Maxima from sourceforge. net and install it, along with some documentation. • Bring laptop to class. 45

MAXIMA 46

maxima. sourceforge. net/misc/max ima-opinions. pdf 47

There are many computer algebra systems • Maxima (successor to Macsyma) – MIT Macsyma, later to Symbolics – DOE Macsyma • Now free under GPL – Can use, modify, bundle according to Gnu Public License – Must release source code in any development 48

All CAS packages are powerful 49

Other high quality software • Mathematica – Elaborate, good graphics – Student versions available for yearly license – Some university-wide licenses (here? ) • Matlab – Currently available in CLDC • Maple – Canadian-made 50

Others, cont. • Derive (now not supported, had been used by TI as a successor to Mu. Math) • Others based on scientific calculators • Reduce – Theoretical math • Cayley – Theoretical math (groups) • Axiom 51

Software is imperfect • All the packages require analysis – don’t just assume the results are correct • Reference: a 1995 study by Michael Webster • www. eng. ysu. edu/~jalam/engr 6924 s 07/se ssions/cas. pdf 52

• means success 53

• means success 54

• means success 55

Example – start xmaxima running 56

Example – opening message of maxima Maxima 5. 18. 1 http: //maxima. sourceforge. net Using Lisp GNU Common Lisp (GCL) GCL 2. 6. 8 (aka GCL) Distributed under the GNU Public License. See the file COPYING. Dedicated to the memory of William Schelter. The function bug_report() provides bug reporting information. 57

Examples from a Maxima session (%i 1) 16+ 25; (%o 1) (%i 2) 56; (%o 2) (%i 3) o 1+02; (%o 3) (%i 4) %o 1 + %o 2; (%o 4) 41 56 o 1 + 2 97 58

Examples from a Maxima session • • (%i 5) 97+97+97 ; (%o 5) (%i 6) 97 * 3; (%o 6) (%i 7) a+b; (%o 7) 291 b+a 59

Examples from a Maxima session (%i 8) (a + b)^2; 60

Examples from a Maxima session (%i 8) (a + b)^2; (%o 8) 2 (b + a) 61

Examples from a Maxima session (%i 8) (a + b)^2; (%o 8) (%i 9) expand ((a+b)^2); 2 (b + a) 62

Examples from a Maxima session (%i 8) (a + b)^2; (%o 8) (%i 9) expand ((a+b)^2); (%o 9) 2 (b + a) 2 2 b +2 ab+a 63

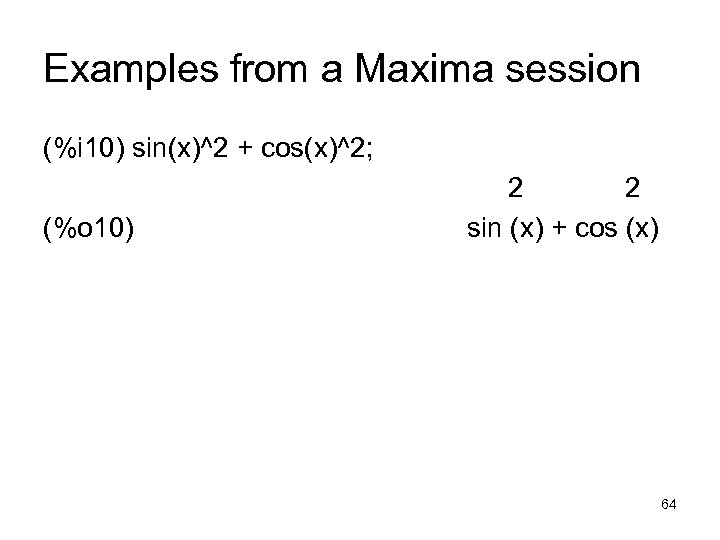Examples from a Maxima session (%i 10) sin(x)^2 + cos(x)^2; (%o 10) 2 2 sin (x) + cos (x) 64

Examples from a Maxima session (%i 10) sin(x)^2 + cos(x)^2; (%o 10) (%i 11) simp(sin(x)^2 + cos(x)^2); 2 2 sin (x) + cos (x) 65

Examples from a Maxima session (%i 10) sin(x)^2 + cos(x)^2; 2 2 sin (x) + cos (x) (%o 10) (%i 11) simp(sin(x)^2 + cos(x)^2); simp evaluates to true Improper name or value in functional position. -- an error. To debug this try debugmode(true); (%i 12) 66

Examples from a Maxima session (%i 12) ratsimp(sin(x)^2 + cos(x)^2); (%o 12) 2 2 sin (x) + cos (x) 67

Examples from a Maxima session (%i 12) ratsimp(sin(x)^2 + cos(x)^2); (%o 12) 2 2 sin (x) + cos (x) ratsimp doesn’t know the “obvious” trig reduction. 68