СХЕМОТЕХНИКА ЭЛЕКТРОННЫЙ КУРС ЛЕКЦИЙ ЛИТЕРАТУРА 1 Угрюмов

СХЕМОТЕХНИКА ЭЛЕКТРОННЫЙ КУРС ЛЕКЦИЙ

ЛИТЕРАТУРА 1. Угрюмов Е. Цифровая схемотехника, – СПб: БХВ, 2004. – 528 с. 2. Фрике К. Вводный курс цифровой электроники, М. : ТЕХНОСФЕРА, 2003. - 432 с. 3. Лачин В. И. , Савелов Н. С. Электроника, Ростов-на. Дону, 2000. – 448 с. 4. Забродин Ю. С. Промышленная электроника, М. : Высшая школа, 1982. – 496 с. 5. Токхейм Р. Основы цифровой электроники, - М. : Мир, 1988. – 392 с. 6. Хоровиц П. , Хилл У. Искусство схемотехники. Том 1. , М. : Мир, 1998. – 432 с.

Цель, задачи, структура и содержание дисциплины «Схемотехника» Определение. Схемотехника, научно техническое направление, охватывающее проблемы проектирования и исследования схем электронных устройств радиотехники и связи, вычислительной техники, автоматики и других областей техники. Цель курса решение задач схемотехнической реализации типовых элементов, узлов, блоков цифровой вычислительной техники. Основная задача схемотехники — синтез (определение структуры) электронных схем, обеспечивающих выполнение определённых функций, и расчёт параметров входящих в них элементов. Теоретической базой схемотехники служат теория линейных и нелинейных электрических цепей, электродинамика, математическое программирование, теория автоматов.

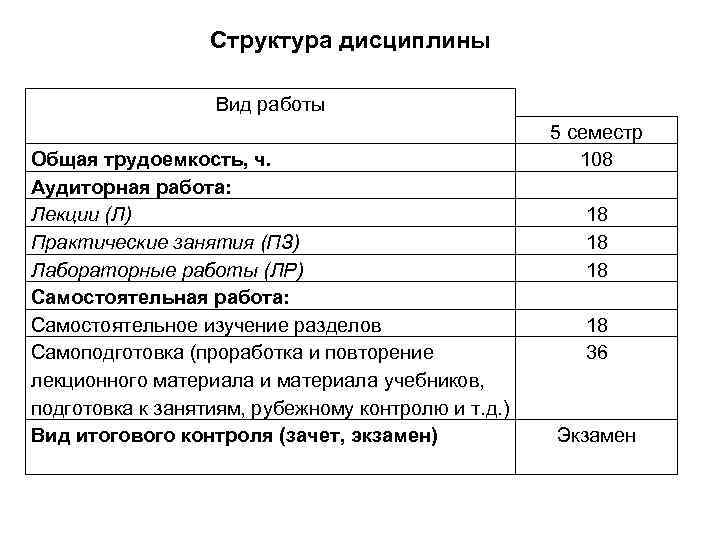Структура дисциплины Вид работы Общая трудоемкость, ч. Аудиторная работа: Лекции (Л) Практические занятия (ПЗ) Лабораторные работы (ЛР) Самостоятельная работа: Самостоятельное изучение разделов Самоподготовка (проработка и повторение лекционного материала и материала учебников, подготовка к занятиям, рубежному контролю и т. д. ) Вид итогового контроля (зачет, экзамен) 5 семестр 108 18 18 36 Экзамен

Содержание дисциплины Разделы 1. Схемотехнические основы построения элементов и узлов цифровых устройств. 2. Функциональные узлы комбинационного типа. 3. Функциональные узлы последовательностного типа. 4. Полупроводниковые запоминающие устройства. 5. Интегральные схемы программируемой логики.

Раздел 1. Схемотехнические основы построения элементов и узлов цифровых устройств 1. 2. 3. 4. 5. Введение в цифровую электронику. Элементная база цифровых устройств. Классификация цифровых интегральных схем. Простейшие модели логических элементов. Статические и динамические характеристики логических элементов. 6. Технологии, применяемые для изготовления логических микросхем. Их характеристики. 7. Типы выходных каскадов ТТЛ и КМОП элементов. 8. Математический аппарат анализа и синтеза цифровых систем.

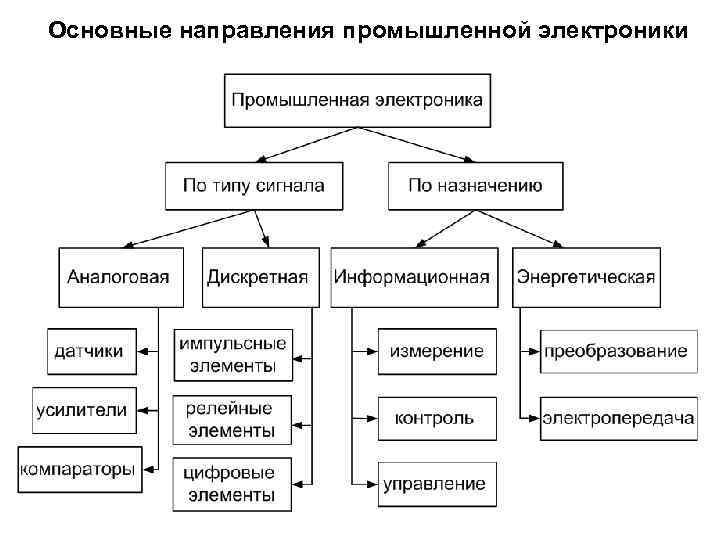Основные направления промышленной электроники

Аналоговые электронные устройства предназначены для приема и передачи электрического сигнала, изменяющегося по закону непрерывной (аналоговой) функции. В аналоговом электронном устройстве каждому конкретному значению реальной физической величины на входе датчика соответствует однозначное, вполне определенное значение выбранного электрического параметра постоянного или переменного тока. Достоинствами аналоговых электронных устройств являются: 1) теоретически максимально достижимые точность и быстродействие; 2) простота устройства. Недостатками являются: 1) низкая помехоустойчивость и нестабильность параметров, обусловленные сильной зависимостью свойств устройства от внешних дестабилизирующих воздействий (температуры, времени, старения элементов, действия внешних полей и т. п. ); 2) большие искажения при передаче на значительные расстояния; низкая энергетическая эффективность.

Дискретные электронные устройства предназначены для приема и передачи электрических сигналов, полученных путем квантования по времени и/или уровню исходной аналоговой функции. Поэтому действующие в них сигналы пропорциональны конечному числу выбранных по определенному закону значений реальной физической величины, отображаемой в виде различных параметров импульсов. К достоинствам дискретных электронных устройств относят следующие: 1) возможность получения существенного превышения мощности в импульсе над средним ее значением; 2) усилительные приборы используют в режиме ключа, при котором рассеиваемая в них мощность минимальна, что повышает коэффициент использования прибора; 3) свойства дискретных устройств в меньшей степени зависят от нестабильности параметров используемых элементов; 4) высокая помехоустойчивость.

Три подкласса дискретных устройств По типу квантования сигнала дискретные электронные устройства делятся на три подкласса: 1. импульсные реализуют квантование исходного сигнала по времени; 2. релейные реализуют квантование исходного сигнала по уровню; 3. цифровые реализуют квантование исходного сигнала как по времени, так и по уровню.

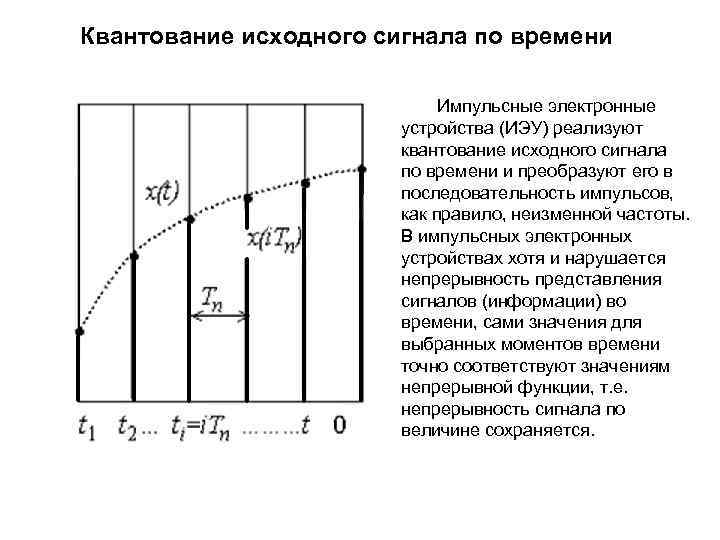Квантование исходного сигнала по времени Импульсные электронные устройства (ИЭУ) реализуют квантование исходного сигнала по времени и преобразуют его в последовательность импульсов, как правило, неизменной частоты. В импульсных электронных устройствах хотя и нарушается непрерывность представления сигналов (информации) во времени, сами значения для выбранных моментов времени точно соответствуют значениям непрерывной функции, т. е. непрерывность сигнала по величине сохраняется.

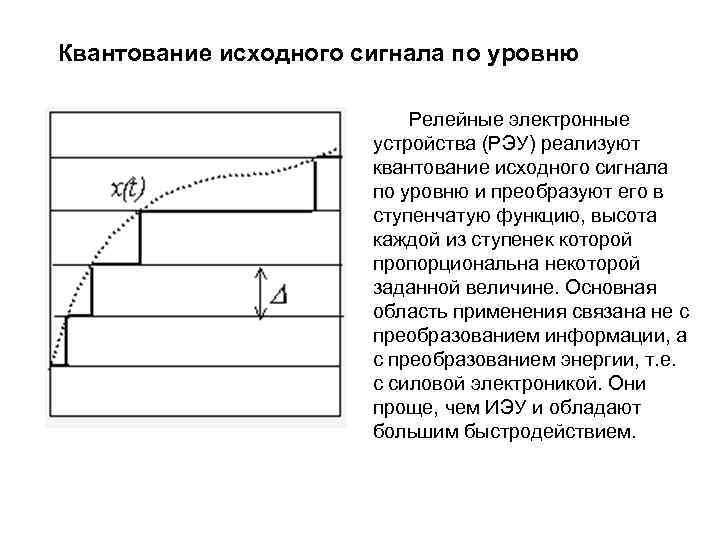Квантование исходного сигнала по уровню Релейные электронные устройства (РЭУ) реализуют квантование исходного сигнала по уровню и преобразуют его в ступенчатую функцию, высота каждой из ступенек которой пропорциональна некоторой заданной величине. Основная область применения связана не с преобразованием информации, а с преобразованием энергии, т. е. с силовой электроникой. Они проще, чем ИЭУ и обладают большим быстродействием.

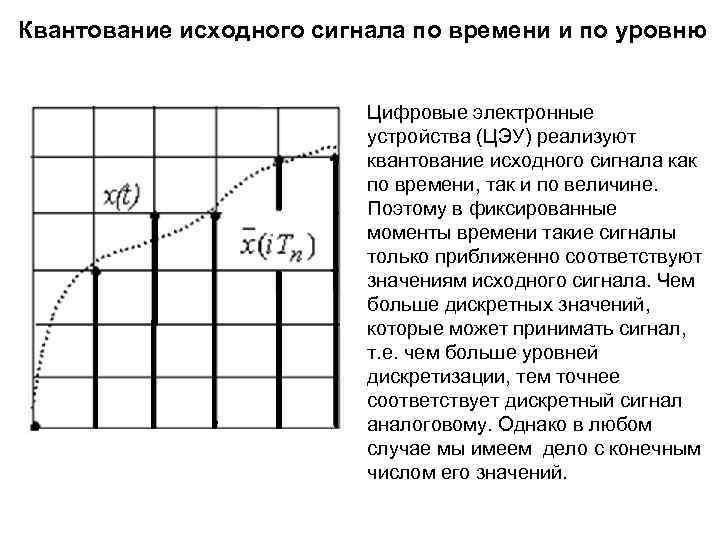Квантование исходного сигнала по времени и по уровню Цифровые электронные устройства (ЦЭУ) реализуют квантование исходного сигнала как по времени, так и по величине. Поэтому в фиксированные моменты времени такие сигналы только приближенно соответствуют значениям исходного сигнала. Чем больше дискретных значений, которые может принимать сигнал, т. е. чем больше уровней дискретизации, тем точнее соответствует дискретный сигнал аналоговому. Однако в любом случае мы имеем дело с конечным числом его значений.

Таким образом, в дискретном сигнале нарушена непрерывность представления информации как по величине, так и во времени. Конечному числу дискретных значений исходной физической величины можно поставить в соответствие некоторое число. Процесс замены дискретных уровней сигнала последовательностью чисел называется кодированием. Устройства, занимающиеся формированием, преобразованием и передачей кодов, поставленных в соответствие реальным значениям физических переменных, называют цифровыми устройствами. 1. 2. 3. 4. Достоинства ЦЭУ: высокая помехоустойчивость, высокая надежность, возможность длительного хранения информации, совместимость с интегральной технологией

Микроэлектроника – это современное направление электроники, охватывающее конструирование, изготовление и применение электронных узлов, блоков и устройств с высокой степенью миниатюризации. Микроэлектроника решает проблемы существенного повышения надежности, уменьшения массогабаритных показателей и стоимости электронной аппаратуры. В основу микроэлектроники положен интегральный принцип изготовления и применения электронных компонентов, при котором каждый компонент представляет собой не отдельно взятый транзистор, диод, резистор, конденсатор и т. д. , а их неразъемное схемное соединение, представляющее собой некоторый узел, блок или целое устройство электронной аппаратуры, в связи с этим компоненты микроэлектроники носят название интегральных микросхем или просто микросхем. Интегральная схема представляет собой совокупность нескольких взаимосвязанных элементов (транзисторов, резисторов, конденсаторов и др. ), изготовленных в едином технологическом цикле, на одной и той же несущей конструкции, и выполняющих одну и ту же функцию преобразования информации.

2. Элементная база цифровых устройств Элементную базу цифровых устройств (ЦУ) составляют интегральные схемы (ИС). Со времени их изобретения (США, 1959 г. ) ИС постоянно совершенствуются и усложняются. Характеристикой сложности ИС является уровень интеграции, оцениваемый либо числом базовых логических элементов, либо числом транзисторов, которые могут быть реализованы на кристалле. Различия в уровне интеграции делят ИС на несколько категорий: 1) МИС малые ИС; 2) СИС средние ИС; 3) БИС большие ИС; 4) СБИС сверхбольшие ИС. Практическое использование находят все категории. МИС реализуют простейшие логические преобразования и обладают универсальностью — даже с помощью одного типа логического элемента (например, И НЕ) можно построить любое ЦУ. В виде СИС выпускаются в готовом виде такие схемы, как малоразрядные регистры, счетчики, дешифраторы, сумматоры и т. п. Номенклатура СИС должна быть более широкой и разнообразной, так как их универсальность снижается. С появлением БИС и СБИС схемы с тысячами и даже миллионами логических элементов стали размещаться на одном кристалле.

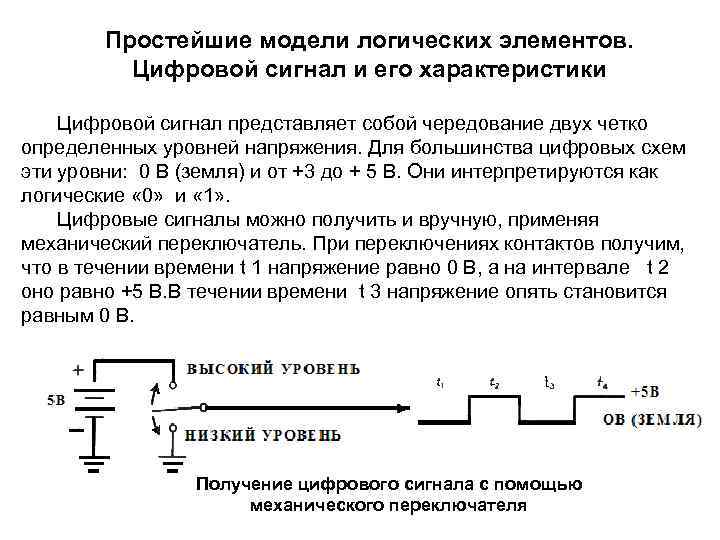Простейшие модели логических элементов. Цифровой сигнал и его характеристики Цифровой сигнал представляет собой чередование двух четко определенных уровней напряжения. Для большинства цифровых схем эти уровни: 0 В (земля) и от +3 до + 5 В. Они интерпретируются как логические « 0» и « 1» . Цифровые сигналы можно получить и вручную, применяя механический переключатель. При переключениях контактов получим, что в течении времени t 1 напряжение равно 0 В, а на интервале t 2 оно равно +5 В. В течении времени t 3 напряжение опять становится равным 0 В. Получение цифрового сигнала с помощью механического переключателя

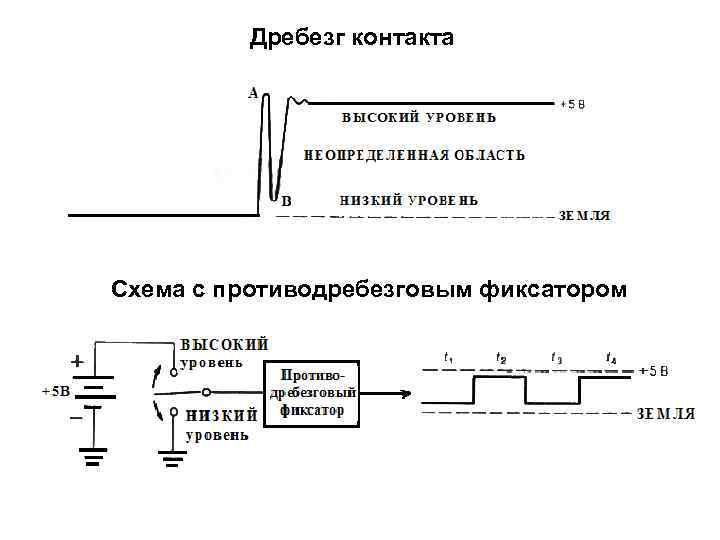Дребезг контакта Схема с противодребезговым фиксатором

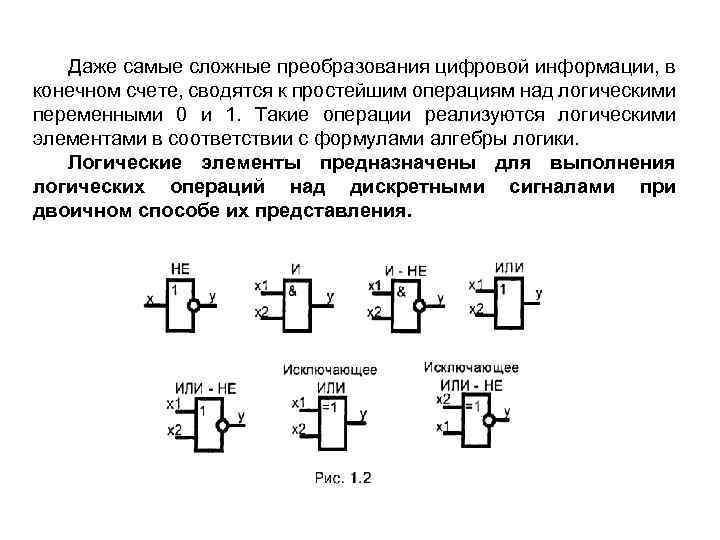Даже самые сложные преобразования цифровой информации, в конечном счете, сводятся к простейшим операциям над логическими переменными 0 и 1. Такие операции реализуются логическими элементами в соответствии с формулами алгебры логики. Логические элементы предназначены для выполнения логических операций над дискретными сигналами при двоичном способе их представления.

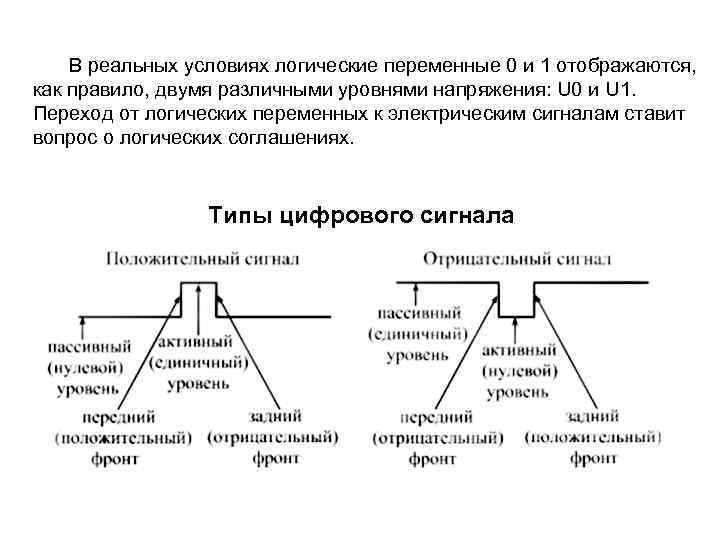В реальных условиях логические переменные 0 и 1 отображаются, как правило, двумя различными уровнями напряжения: U 0 и U 1. Переход от логических переменных к электрическим сигналам ставит вопрос о логических соглашениях. Типы цифрового сигнала

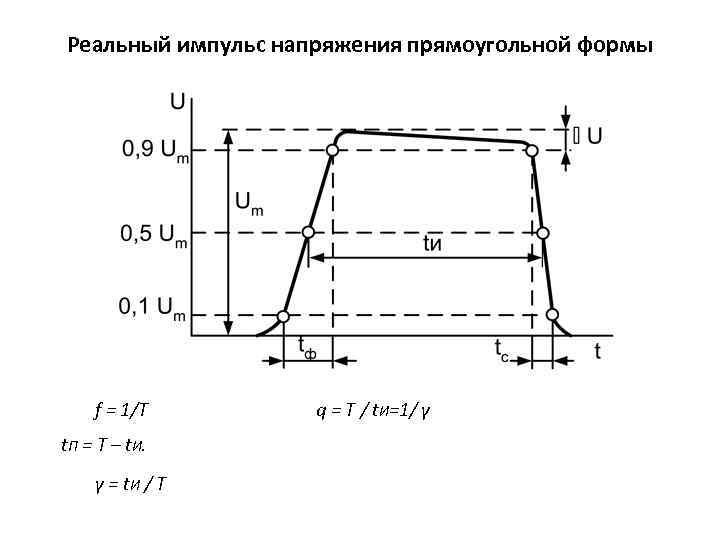Реальный импульс напряжения прямоугольной формы f = 1/Т t. П = Т – t. И. γ = t. И / T q = T / t. И=1/ γ

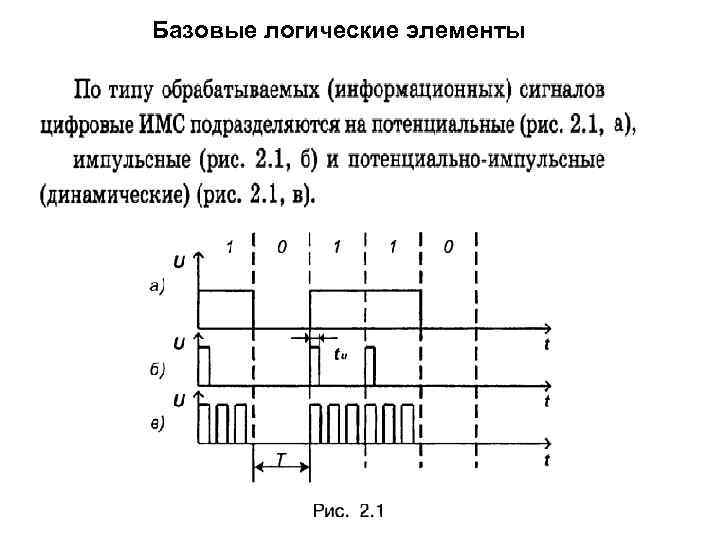Базовые логические элементы

Основным отличительным признаком элементов потенциального типа является наличие связи по постоянному току между входами и выходами. По функциональному назначению элементы делятся на: 1) логические элементы , реализующие логические функции из базисной системы; 2) элементы памяти, предназначенные для запоминания и хранения информации; 3) специальные, для физического преобразования электрических сигналов (усиления, формирования, генерации и т. п. ).

Широкое распространение получили логические микросхемы на биполярных транзисторах: транзисторная логика (ТЛ) с различными видами связей: 1) ТЛНС (с непосредственными связями), 2) РСТЛ (с резистивными связями), 3) РЕТЛ (с резистивно емкостными связями), 4) ДТЛ (диодно транзисторная логика), 5) ТТЛ (транзисторно транзисторная логика); 6) ТТЛШ (схемы с барьером Шоттки). Современные интегральные микросхемы чаще всего выполнены на полевых транзисторах КМОП технологии.

Характеристики логических микросхем Статические характеристики: 1. 2. 3. 4. 5. четыре значения напряжений и четыре значения токов; нагрузочная способность; амплитудно передаточная характеристика; статическая помехоустойчивость; потребляемая мощность. Динамические характеристики: 1. быстродействие; 2. динамическая помехоустойчивость; 3. динамическая мощность.

Статические параметры логических элементов В качестве важнейших статических параметров приводятся четыре значения напряжений и четыре значения токов. Четыре значения напряжений задают границы отображения переменных (0 и 1) на выходе и входе элемента: Четыре значения токов — входные и выходные токи в обоих логических состояниях. При высоком уровне выходного напряжения из элемента — источника ток вытекает, цепи нагрузки ток поглощают. При низком уровне выходного напряжения элемента источника ток нагрузки втекает в этот элемент, а из входных цепей элементов приемников токи вытекают.

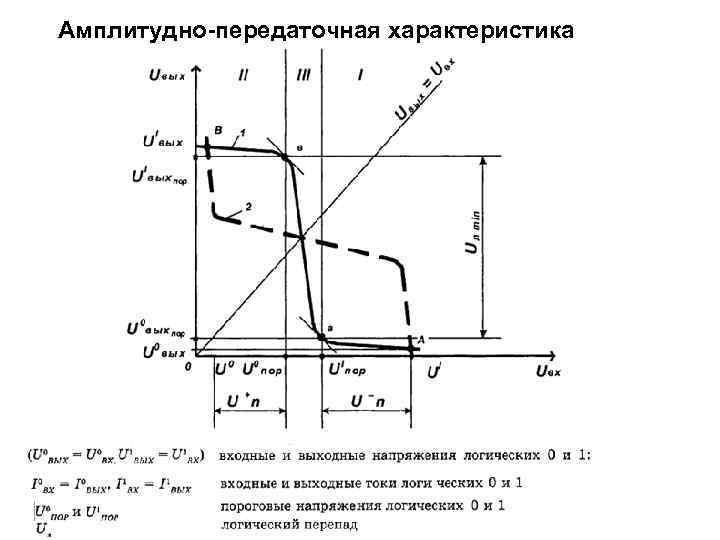Амплитудно-передаточная характеристика

Мощности потребления логических элементов При разработке ЦУ требуется оценивать мощности их потребления, чтобы сформулировать требования к источникам питания и конструкции вода. При этом суммируются мощности, рассеиваемые логическими и другими элементами схемы, а также межсоединениями. Мощности, потребляемые элементами, делят на статические и динамические. Статическая мощность потребляется элементом, который не переключается. При переключении потребляется дополнительно динамическая мощность, которая пропорциональна частоте переключения элемента. Таким образом, полная мощность зависит от частоты переключения элемента, что и следует учитывать при ее подсчете.

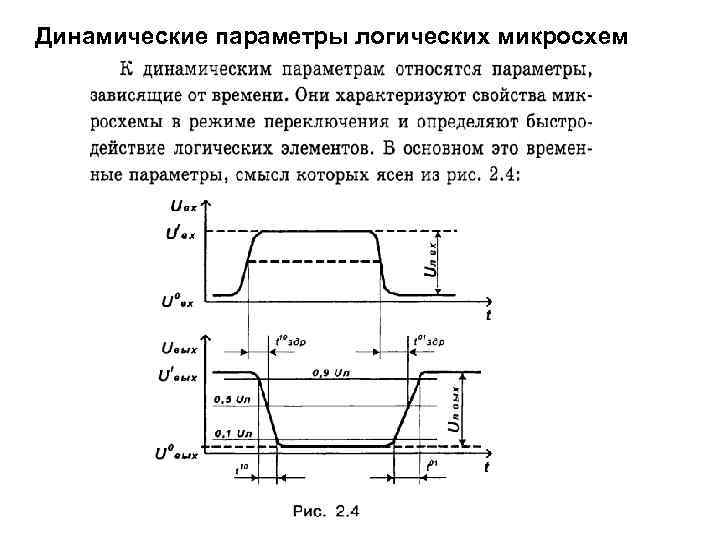Динамические параметры логических микросхем

Технологии изготовления логических микросхем 1. Диодно-резисторные логические схемы (ДРЛ)

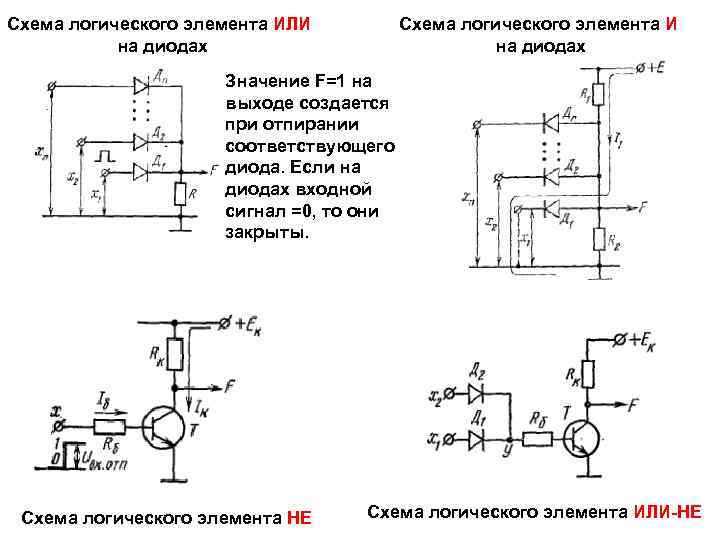Схема логического элемента ИЛИ на диодах Схема логического элемента И на диодах Значение F=1 на выходе создается при отпирании соответствующего диода. Если на диодах входной сигнал =0, то они закрыты. Схема логического элемента НЕ Схема логического элемента ИЛИ-НЕ

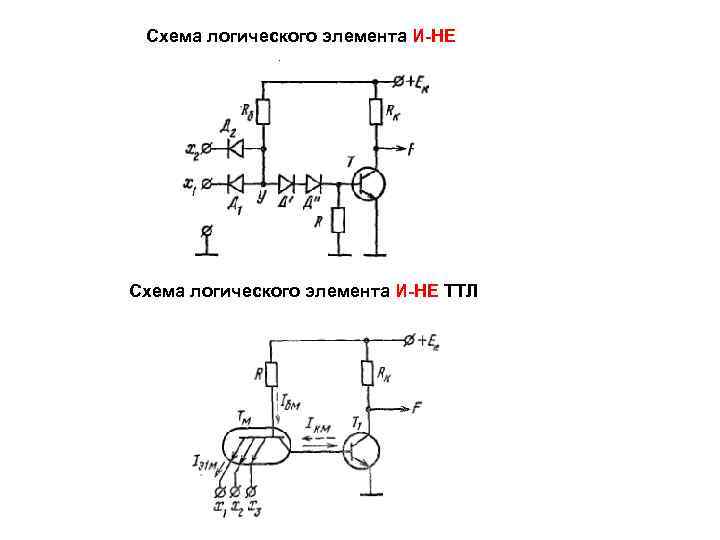Схема логического элемента И-НЕ ТТЛ

2. Транзисторно-транзисторные логические схемы (ТТЛ, ТТЛШ)

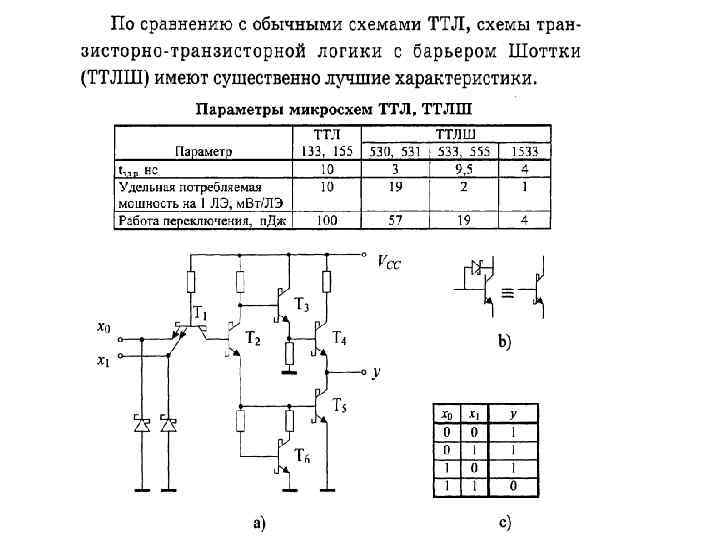
3. Эмиттерно-связанная логика (ЭСЛ)

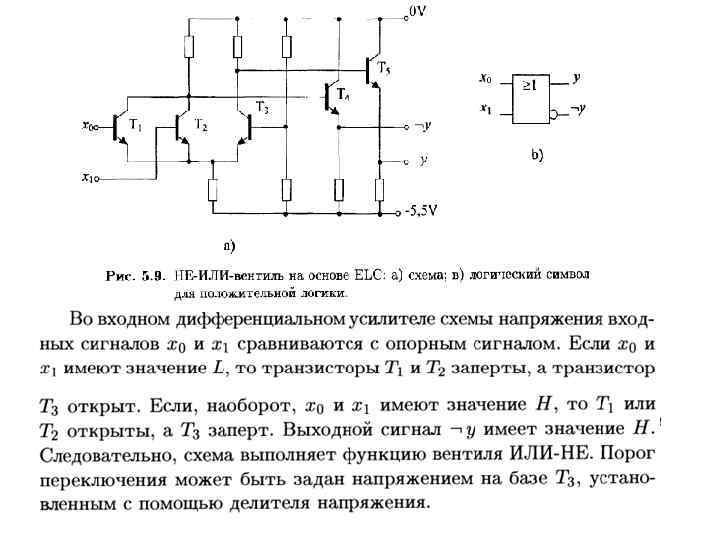
4. Интегральная инжекционная логика

Достоинства и недостатки интегральной инжекционной логики

5. Логические микросхемы МОП и КМОП

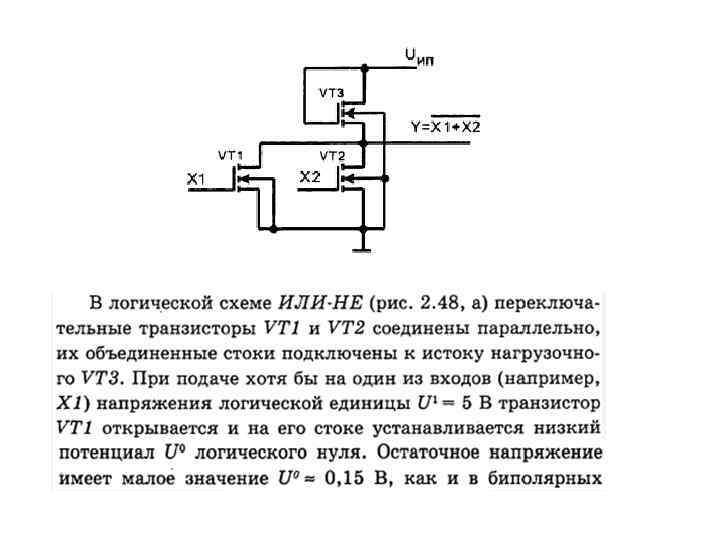
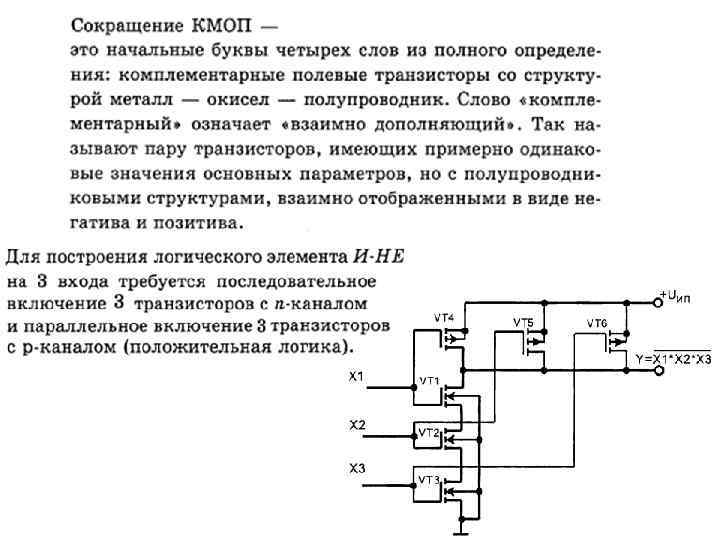
Математический аппарат анализа и синтеза цифровых систем Функции алгебры логики (ФАЛ) определяют однозначное соответствие двоичных наборов аргументов логическому нулю или логической единице. Для задания ФАЛ используют 4 способа: 1. 2. 3. 4. Таблицы истинности; Аналитические выражения; Последовательность десятичных чисел (цифровая форма); Словесное описание.

Каждой двоичной переменной, например х, ставится в соответствие обратная переменная (инверсная) такая, что: В алгебре логики в случае одной переменной х действуют следующие правила (аксиомы):

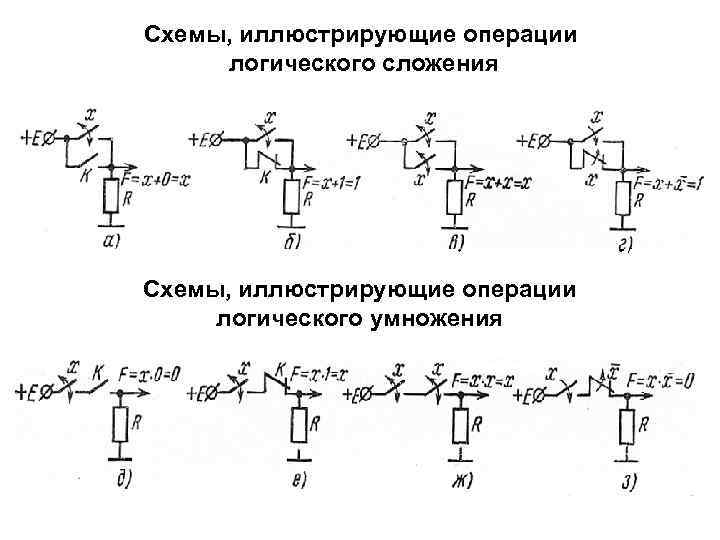Схемы, иллюстрирующие операции логического сложения Схемы, иллюстрирующие операции логического умножения

Логические функции двух переменных Существует 16 функций двух переменных.

Тождества и законы алгебры логики

К основным законам относятся законы инверсии для логических сложения и умножения (теоремы де Моргана). 1) Инверсия суммы переменных есть произведение их инверсий. 2) Инверсия произведений переменных есть сумма их инверсий. В качестве примера определим инверсию функции По закону де Моргана получим следующее выражение:

Пусть функция F задана в виде таблицы. Для комбинации переменных 2, 7, 8 эта функция истинна (F = 1), что означает для указанных комбинаций равенство единице следующих произведений: Комбинации переменных, при которых функция истинна, называют конституентами единицы, или минтермами. Представление логической функции в виде суммы минтермов определяет ее СДНФ, т. е. в данном случае:

Функция, определенная таблицей истинности, может быть представлена и нулевыми значениями, т. е. F = 0 или Воспользовавшись законом инверсии, приходим к записи функции в СКНФ: Такие суммы называют конституентами нуля или макстермами.

Понятие базиса Любая логическая функция, представленная таблицей истинности, может быть представлена в форме СДНФ или СКНФ. Каждая из этих формул записана с помощью логического сложения, умножения и отрицания. В общем случае необходимо иметь элементы, выполняющие операции И, ИЛИ, НЕ. Такой набор элементов называется функционально полной системой логических элементов или логическим базисом. Базис из элементов: И, ИЛИ, НЕ называется основным. Однако, число необходимых элементов в такой системе можно уменьшить, исключив из неё либо элемент ИЛИ, либо элемент И. Например, в соответствии с теоремой де Моргана, имеем Отсюда следует, что операцию логического ИЛИ можно заменить операцией И над инверсными значениями переменных , а затем к результату применить операцию инверсии и тем самым исключить элемент ИЛИ.

При схемной реализации функционально полных систем с минимальным логическим базисом используют универсальные логические элементы: ИЛИ НЕ, И НЕ и И ИЛИ НЕ Элемент ИЛИ НЕ Рисунок 5, а) осуществляет логическую операцию , называемую также стрелкой Пирса. Элемент И НЕ (Рисунок 5, б) осуществляет логическую операцию и называется штрих Шеффера. Элемент И ИЛИ НЕ (Рисунок 5, в) осуществляет операцию и является элементом сложного базиса.

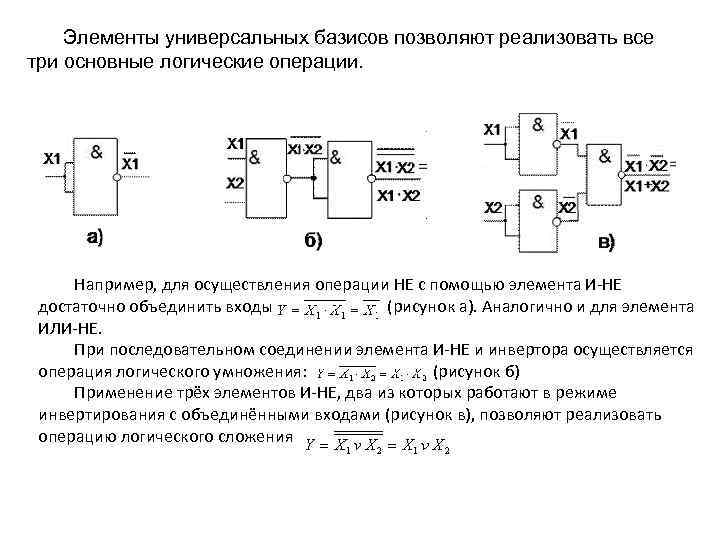Элементы универсальных базисов позволяют реализовать все три основные логические операции. Например, для осуществления операции НЕ с помощью элемента И-НЕ достаточно объединить входы (рисунок а). Аналогично и для элемента ИЛИ-НЕ. При последовательном соединении элемента И-НЕ и инвертора осуществляется операция логического умножения: (рисунок б) Применение трёх элементов И-НЕ, два из которых работают в режиме инвертирования с объединёнными входами (рисунок в), позволяют реализовать операцию логического сложения

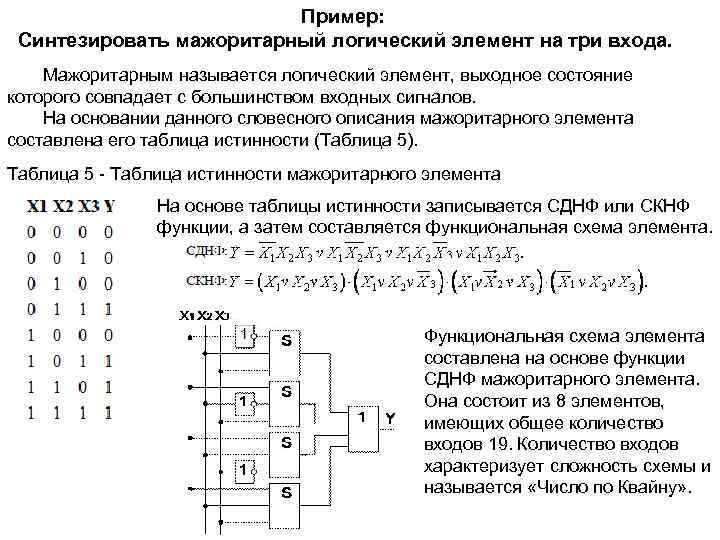Пример: Синтезировать мажоритарный логический элемент на три входа. Мажоритарным называется логический элемент, выходное состояние которого совпадает с большинством входных сигналов. На основании данного словесного описания мажоритарного элемента составлена его таблица истинности (Таблица 5). Таблица 5 Таблица истинности мажоритарного элемента На основе таблицы истинности записывается СДНФ или СКНФ функции, а затем составляется функциональная схема элемента. Функциональная схема элемента составлена на основе функции СДНФ мажоритарного элемента. Она состоит из 8 элементов, имеющих общее количество входов 19. Количество входов характеризует сложность схемы и называется «Число по Квайну» .

Минимизация логических формул Однозначная зависимость сложности логической формулы и функциональной схемы логического устройства приводят к выводу необходимости минимизации структурной формулы логического устройства. Минимизация осуществляется с использованием основных соотношений, законов и теорем алгебры логики. Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n мерного булева куба. Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs» , и были призваны помочь упростить цифровые электронные схемы. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Принципы минимизации Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например: Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов. Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

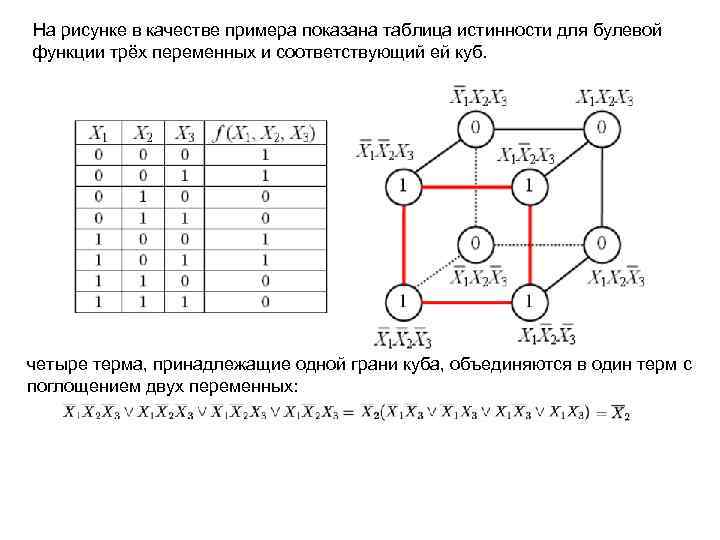На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб. четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

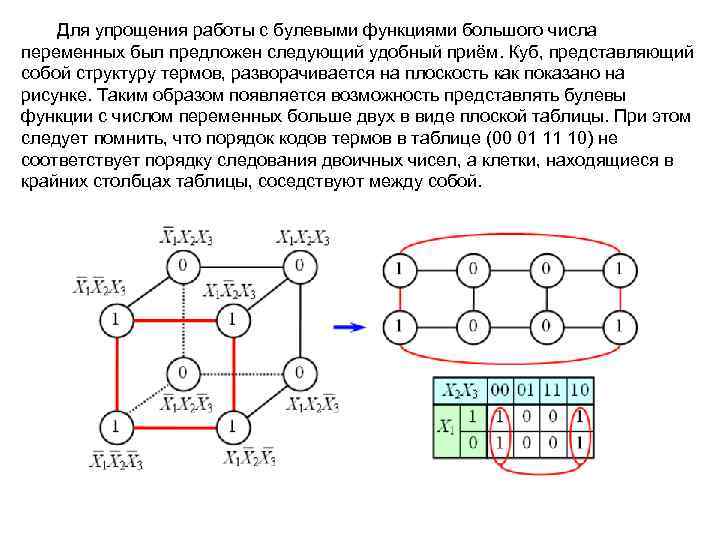Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Описание Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2 -х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т. о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации. Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули.

Сама минимизация производится по следующим правилам ( для ДНФ): 1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули; 2. Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки); 3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну; 4. Область должна быть как можно больше, а количество областей как можно меньше; 5. Области могут пересекаться; 6. Возможно несколько вариантов покрытия. Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.

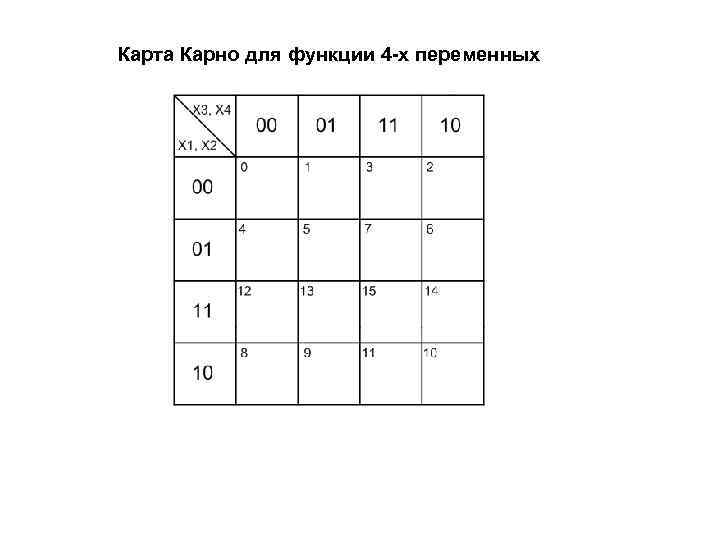Карта Карно для функции 4 -х переменных

Пример заполнения карты Карно для функции

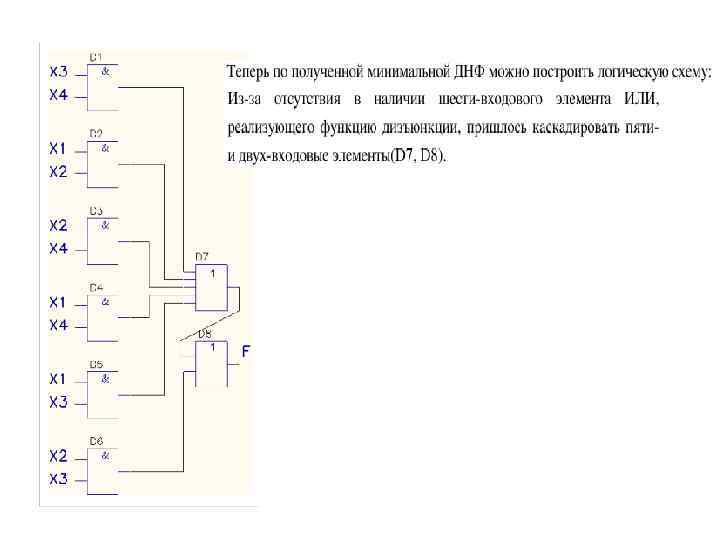
Функциональные узлы комбинационного типа Комбинационным называют функциональные узлы, которые не содержат элементов памяти. Состояние такого узла однозначно определяется комбинацией входных сигналов и не зависит от предыдущего состояния. К ним относятся следующие устройства: преобразователи кода; двоичные дешифраторы; приоритетные и полные двоичные шифраторы, мультиплексоры и демультиплексоры; схемы контроля; двоичные сумматоры; компараторы; арифметическо логические устройства; матричные умножители.

Мультиплексор Устройство, которое осуществляет выборку одного из нескольких входов и подключает его к своему выходу по действием управляющего (адресного) кода, называется мультиплексором. Мультиплексор имеет информационные входы (Х 0, Х 1…. Хn), адресные входы (A 0, A 1…Am), вход для подачи разрешающего сигнала Е и один выход F. Вход разрешения (стробирования) Е позволяет избежать появления на выходах ложных сигналов при чередующихся на входе наборах, кодовое расстояние между которыми больше единицы.

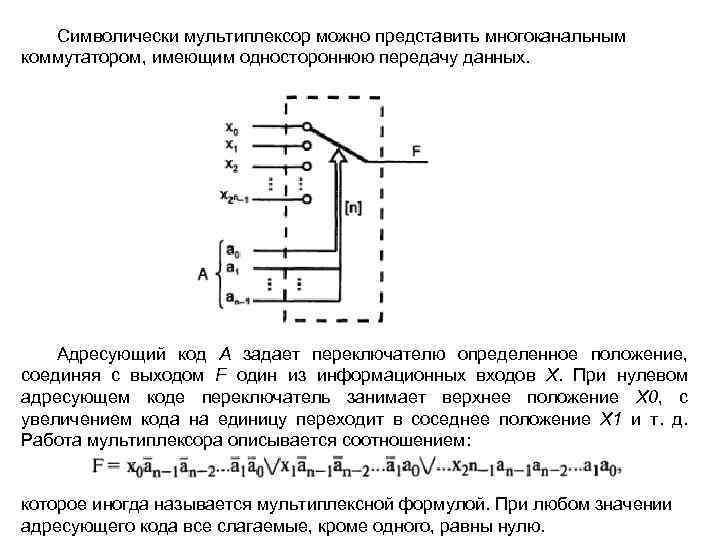Символически мультиплексор можно представить многоканальным коммутатором, имеющим одностороннюю передачу данных. Адресующий код А задает переключателю определенное положение, соединяя с выходом F один из информационных входов Х. При нулевом адресующем коде переключатель занимает верхнее положение Х 0, с увеличением кода на единицу переходит в соседнее положение Х 1 и т. д. Работа мультиплексора описывается соотношением: которое иногда называется мультиплексной формулой. При любом значении адресующего кода все слагаемые, кроме одного, равны нулю.

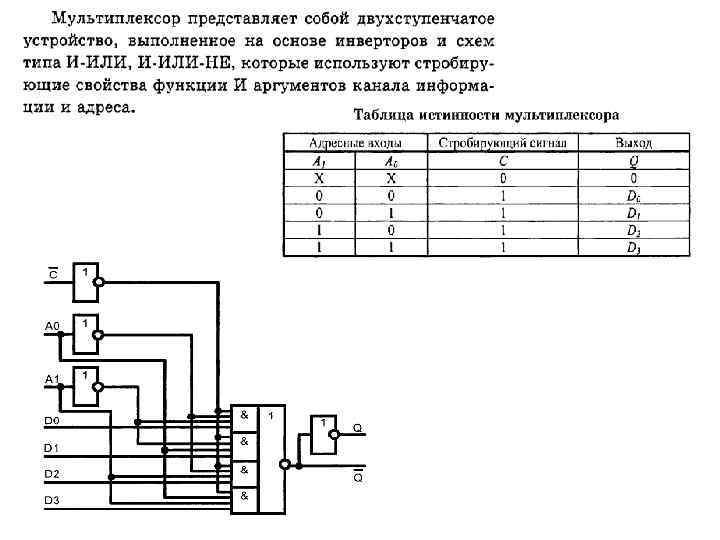
Для обозначения коммутационных возможностей мультиплексора пользуются условной записью где n – это число информационных входов. В зависимости от соотношения числа информационных входов n и числа адресных входов m мультиплексоры делятся на полные и неполные. Если выполняется условие то мультиплексор полный, в противном случае – неполный. Наибольшее распространение получили мультиплексоры: Для неполных мультиплексоров число входов может быть любым, но не больше, чем . Выходы мультиплексора называют разрядами. Например, 4 канальный 2 разрядный мультиплексор имеет 2 выхода, на каждый из которых может передаваться один из 4 х входных сигналов. Некоторые мультиплексоры могут иметь выход с тремя состояниями: 0; 1; третье состояние отключенный выход (выходное сопротивление равно бесконечности), обозначается ОЕ

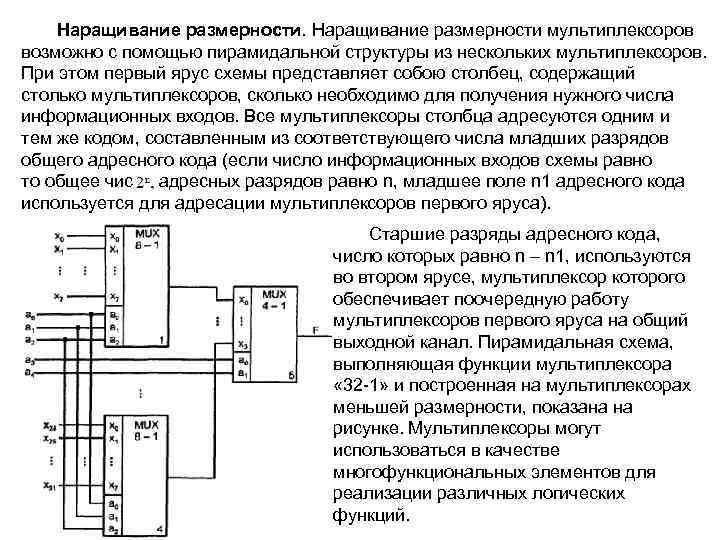Наращивание размерности мультиплексоров возможно с помощью пирамидальной структуры из нескольких мультиплексоров. При этом первый ярус схемы представляет собою столбец, содержащий столько мультиплексоров, сколько необходимо для получения нужного числа информационных входов. Все мультиплексоры столбца адресуются одним и тем же кодом, составленным из соответствующего числа младших разрядов общего адресного кода (если число информационных входов схемы равно то общее число адресных разрядов равно n, младшее поле n 1 адресного кода используется для адресации мультиплексоров первого яруса). Старшие разряды адресного кода, число которых равно n – n 1, используются во втором ярусе, мультиплексор которого обеспечивает поочередную работу мультиплексоров первого яруса на общий выходной канал. Пирамидальная схема, выполняющая функции мультиплексора « 32 1» и построенная на мультиплексорах меньшей размерности, показана на рисунке. Мультиплексоры могут использоваться в качестве многофункциональных элементов для реализации различных логических функций.

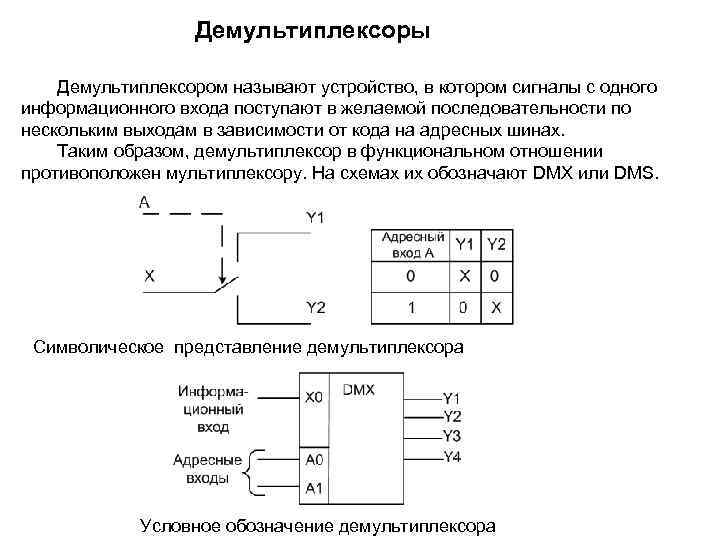Демультиплексоры Демультиплексором называют устройство, в котором сигналы с одного информационного входа поступают в желаемой последовательности по нескольким выходам в зависимости от кода на адресных шинах. Таким образом, демультиплексор в функциональном отношении противоположен мультиплексору. На схемах их обозначают DMX или DMS. Символическое представление демультиплексора Условное обозначение демультиплексора

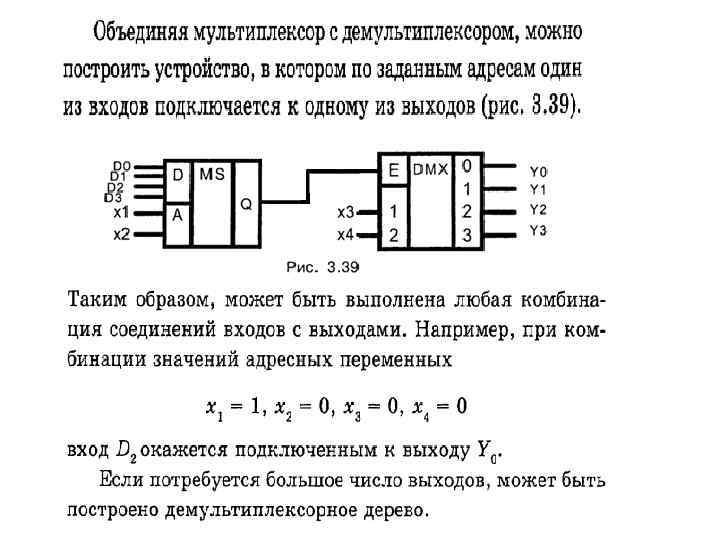
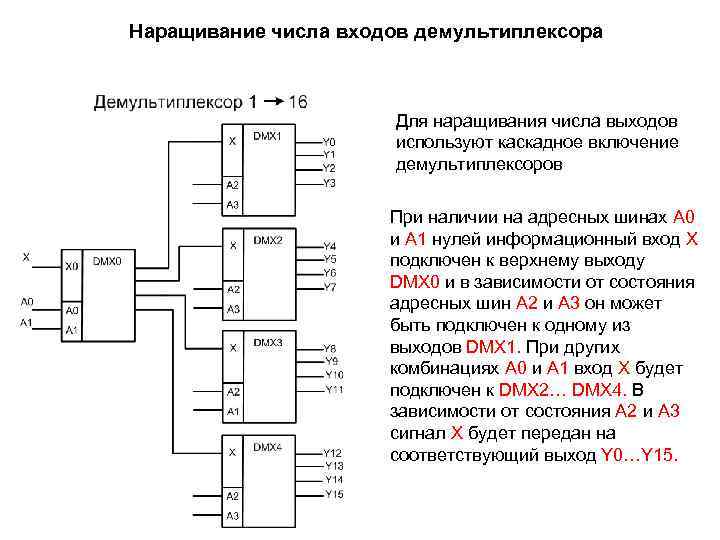Наращивание числа входов демультиплексора Для наращивания числа выходов используют каскадное включение демультиплексоров При наличии на адресных шинах А 0 и А 1 нулей информационный вход Х подключен к верхнему выходу DMX 0 и в зависимости от состояния адресных шин А 2 и А 3 он может быть подключен к одному из выходов DMX 1. При других комбинациях А 0 и А 1 вход Х будет подключен к DMX 2… DMX 4. В зависимости от состояния А 2 и А 3 сигнал Х будет передан на соответствующий выход Y 0…Y 15.

Дешифратор (декодер) – устройство с несколькими входами и выходами, у которого определенным комбинациям входных сигналов соответствует активное состояние одного из выходов, т. е. дешифратор является обращенным по входам демультиплексором, у которого адресные входы стали информационными, а бывший информационный вход стал входом разрешения. Двоичные дешифраторы преобразуют двоичный код в код « 1 из N» . Активным всегда является только один выход дешифратора. В условном обозначении дешифраторов проставляются буквы DC (от английского Decoder). Входы дешифратора принято обозначать их двоичными весами 1 2 4 8. Кроме информационных входов дешифратор обычно имеет один или более входов разрешения работы обозначаемых как EN (Enable). Часто дешифратор имеет инверсные выходы. В этом случае только один выход имеет нулевое значение, а все остальные единичное.

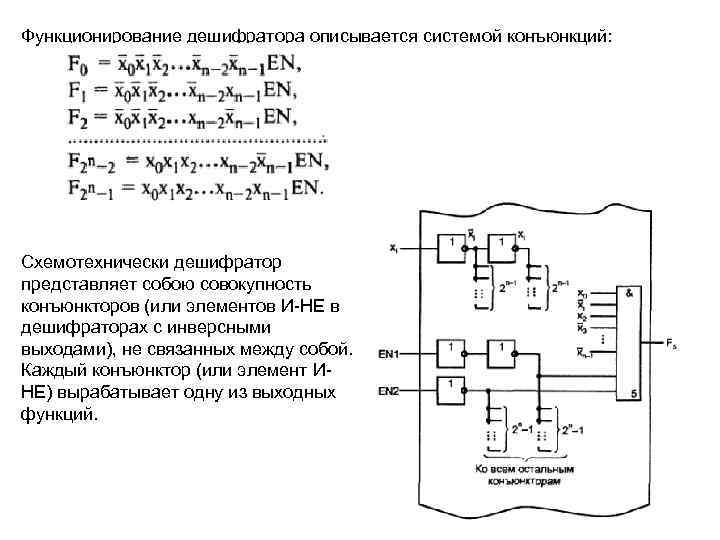Функционирование дешифратора описывается системой конъюнкций: Схемотехнически дешифратор представляет собою совокупность конъюнкторов (или элементов И НЕ в дешифраторах с инверсными выходами), не связанных между собой. Каждый конъюнктор (или элемент И НЕ) вырабатывает одну из выходных функций.

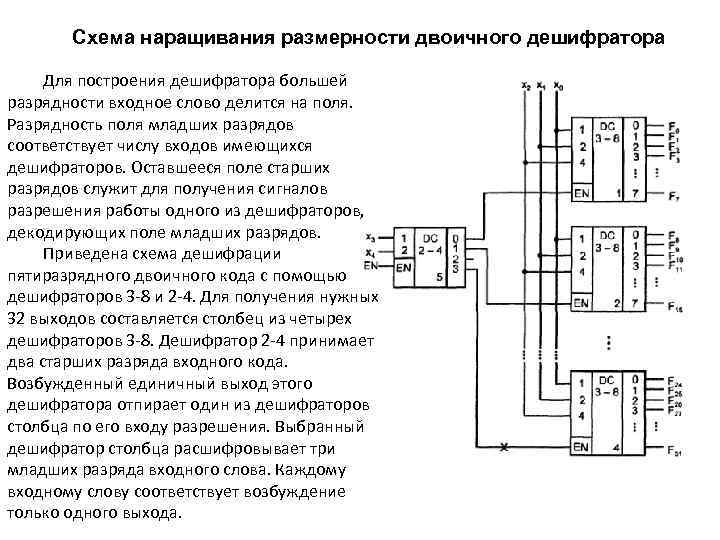Схема наращивания размерности двоичного дешифратора Для построения дешифратора большей разрядности входное слово делится на поля. Разрядность поля младших разрядов соответствует числу входов имеющихся дешифраторов. Оставшееся поле старших разрядов служит для получения сигналов разрешения работы одного из дешифраторов, декодирующих поле младших разрядов. Приведена схема дешифрации пятиразрядного двоичного кода с помощью дешифраторов 3 -8 и 2 -4. Для получения нужных 32 выходов составляется столбец из четырех дешифраторов 3 -8. Дешифратор 2 -4 принимает два старших разряда входного кода. Возбужденный единичный выход этого дешифратора отпирает один из дешифраторов столбца по его входу разрешения. Выбранный дешифратор столбца расшифровывает три младших разряда входного слова. Каждому входному слову соответствует возбуждение только одного выхода.

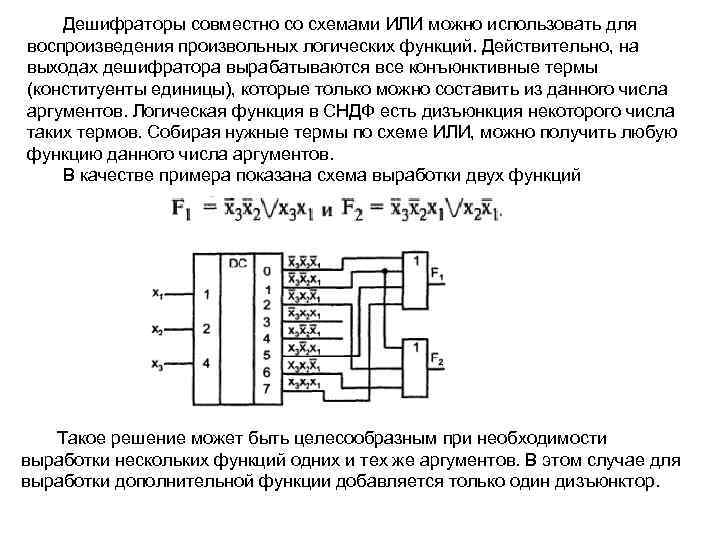Дешифраторы совместно со схемами ИЛИ можно использовать для воспроизведения произвольных логических функций. Действительно, на выходах дешифратора вырабатываются все конъюнктивные термы (конституенты единицы), которые только можно составить из данного числа аргументов. Логическая функция в СНДФ есть дизъюнкция некоторого числа таких термов. Собирая нужные термы по схеме ИЛИ, можно получить любую функцию данного числа аргументов. В качестве примера показана схема выработки двух функций Такое решение может быть целесообразным при необходимости выработки нескольких функций одних и тех же аргументов. В этом случае для выработки дополнительной функции добавляется только один дизъюнктор.

Дешифраторы и демультиплексоры в виде серийных ИМС средней степени интеграции широко используются в информационно измерительной технике и микропроцессорных системах управления, в частности, в качестве коммутаторов распределителей информационных сигналов и синхроимпульсов, для демультиплексирования данных и адресной логики в запоминающих устройствах, а также для преобразования двоично десятичного кода в десятичный с целью управления индикаторными и печатающими устройствами. Дешифраторы как самостоятельные изделия электронной техники имеют 4, 8 или 16 выходов. Если требуется большее число выходов, дешифраторы наращиваются в систему.

Шифраторы

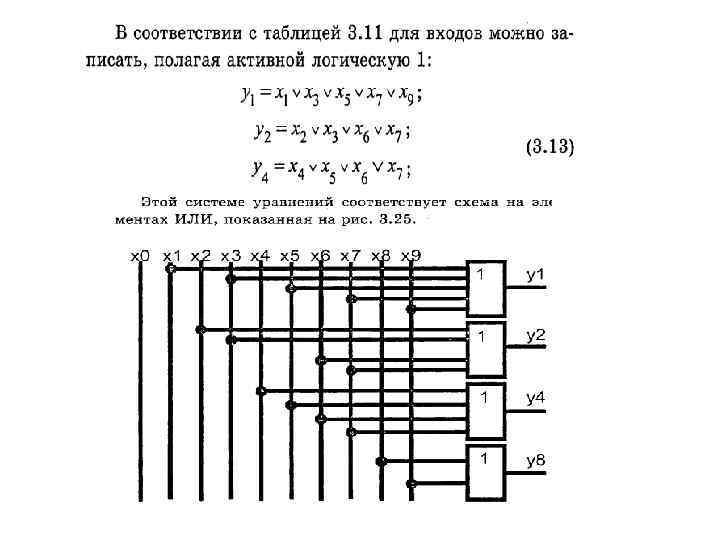
Приоритетные и двоичные шифраторы. Двоичные шифраторы выполняют операцию, обратную по отношению к операции дешифратора: они преобразуют код « 1 из N» в двоичный. При возбуждении одного из входов шифратора на его выходе формируется двоичный код номера возбужденной входной линии. Полный двоичный шифратор имеет входов и n выходов. Приоритетные шифраторы выполняют более сложную операцию. При работе ЭВМ и в других устройствах часто решается задача определения приоритетного претендента на пользование каким либо ресурсом. Несколько конкурентов выставляют свои запросы на обслуживание, которые не могут быть удовлетворены одновременно. Нужно выбрать того, кому предоставляется право первоочередного обслуживания. Простейший вариант решения указанной задачи — присвоение каждому источнику запросов фиксированного приоритета. Например, группа из восьми запросов R 7. . . R 0 (R от английского Request) формируется так, что высший приоритет имеет источник номер семь, а далее приоритет уменьшается от номера к номеру. Самый младший приоритет у нулевого источника — он будет обслуживаться только при отсутствии всех других запросов. Если имеются одновременно несколько запросов, обслуживается запрос с наибольшим номером. Приоритетный шифратор вырабатывает на выходе двоичный номер старшего запроса.

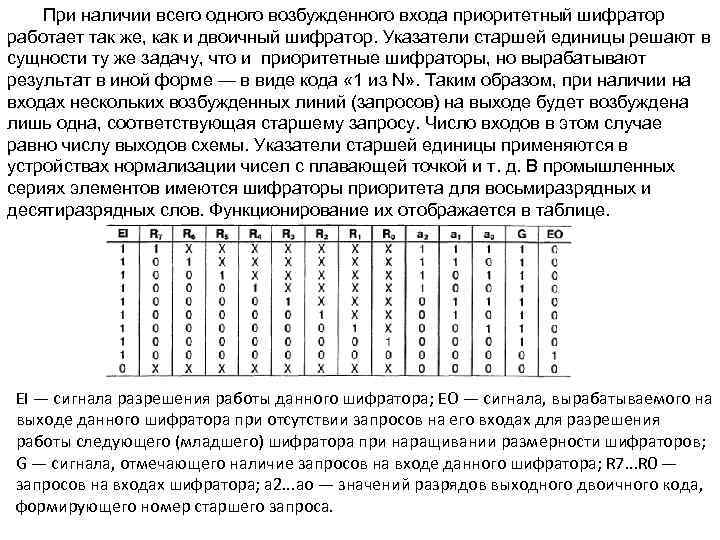При наличии всего одного возбужденного входа приоритетный шифратор работает так же, как и двоичный шифратор. Указатели старшей единицы решают в сущности ту же задачу, что и приоритетные шифраторы, но вырабатывают результат в иной форме — в виде кода « 1 из N» . Таким образом, при наличии на входах нескольких возбужденных линий (запросов) на выходе будет возбуждена лишь одна, соответствующая старшему запросу. Число входов в этом случае равно числу выходов схемы. Указатели старшей единицы применяются в устройствах нормализации чисел с плавающей точкой и т. д. В промышленных сериях элементов имеются шифраторы приоритета для восьмиразрядных и десятиразрядных слов. Функционирование их отображается в таблице. EI — сигнала разрешения работы данного шифратора; ЕО — сигнала, вырабатываемого на выходе данного шифратора при отсутствии запросов на его входах для разрешения работы следующего (младшего) шифратора при наращивании размерности шифраторов; G — сигнала, отмечающего наличие запросов на входе данного шифратора; R 7. . . R 0 — запросов на входах шифратора; а 2. . . ао — значений разрядов выходного двоичного кода, формирующего номер старшего запроса.

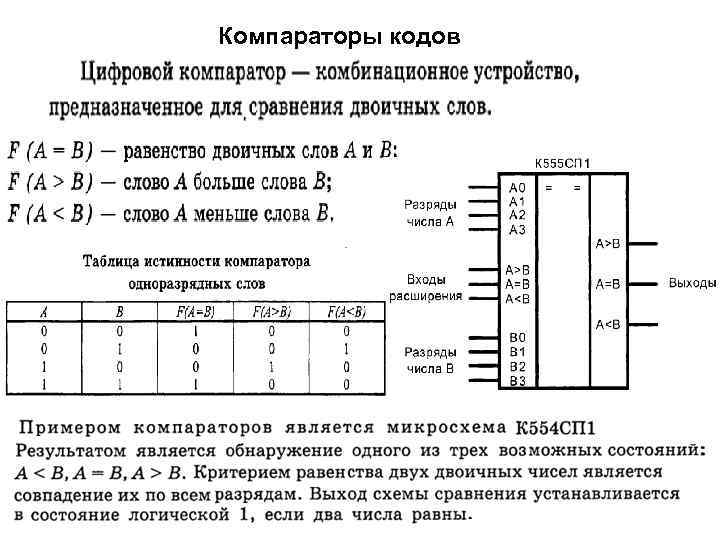Компараторы кодов

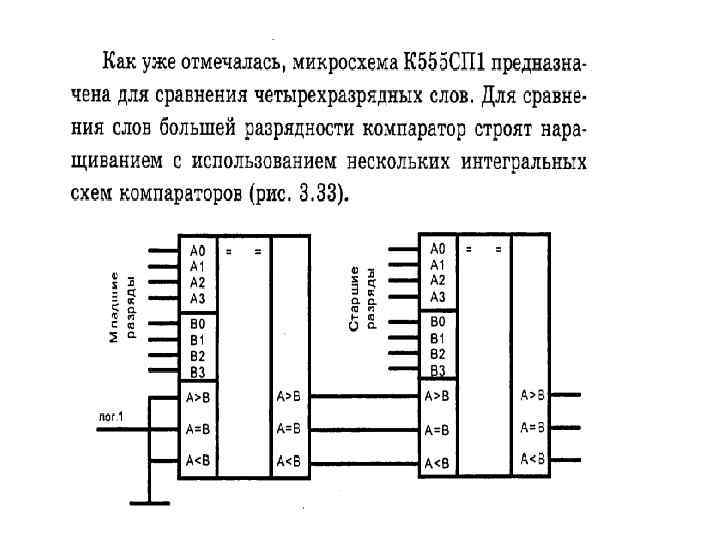
Регистры Регистр – последовательностное устройство, осуществляющее запись, хранение, сдвиг и выдачу чисел в виде многоразрядного двоичного кода (от англ. Register – регистрировать, фиксировать) Запоминающим элементом в регистре служат триггеры. Число триггеров равно числу разрядов хранимых чисел. Схема регистра служит для ввода/вывода хранимых чисел, преобразования их кодов, сдвига кодов на определённое число разрядов. В регистрах выполняются следующие операции: Ввод и вывод информации; Хранение информации; Сдвиг вправо или влево на определенное число разрядов; Преобразование кода числа из последовательного в параллельный.

По способу приема информации регистры подразделяются: параллельные, информация записывается и считывается только в параллельной форме (статические – построены на триггерах и могут хранить информацию долго при наличии Uпит); последовательные (сдвиговые) – запись и считывание происходит только в последовательной форме; последовательно параллельные, используются для преобразования кода из параллельного в последовательный и наоборот. По числу каналов передачи информации: - однофазного типа; парафазного типа. В однофазных ввод (вывод) может производиться только в прямом или только в обратном коде. В парафазных возможен ввод и вывод как в прямом так и в обратном кодах. Вид осуществляемого ввода (вывода) определяется сигналами управления. По способу тактирования: однотактные, синхронизируемые одной управляющей последовательностью; двухтактные; многотактные, управляемые несколькими последовательностями импульсов.

Исходным состоянием регистра является "0". После ввода двоичного числа триггеры переходят в состояние, соответствующее разрядам вводимого числа. Эти значения хранятся до момента передачи другому устройству или до ввода в регистр другого числа или обнуления. В параллельном регистре приём и выдача слов производиться одновременно по всем разрядам. Также в них могут производиться поразрядные логические операции с хранимым или вновь вводимым числом. Вид логической операции зависит от вида триггеров. В последовательных регистрах с помощью сдвигающих (синхронизирующих) импульсов организуется сдвиг кода хранимого числа при каждом сдвигающем импульсе. Сдвиговый регистр может быть нереверсивным (однонаправленным сдвигом), а может быть и реверсивным (с возможностью сдвига в обоих направлениях). Для них предусмотрен специальный вход включения режима направления сдвига. В информационной технике регистры применяются для преобразования последовательного кода в параллельный и обратно.

Параллельные регистры (регистры памяти) это устройства, предназначенные для записи, хранения и выдачи информации, представленной в виде двоичных кодов. Для хранения каждого двоичного разряда в регистре используется одна триггерная ячейка. Для запоминания многоразрядных слов необходимое число триггеров объединяют вместе и рассматривают как единый функциональный узел регистр. Если регистр построен на триггерах защелках, то его называют регистр-защелка. Типовыми внешними связями регистра являются информационные входы D, вход сигнала записи (или загрузки) С, вход гашения R, выходы триггеров Q. В упрощенном варианте регистр может не иметь входа гашения и инверсных выходов.

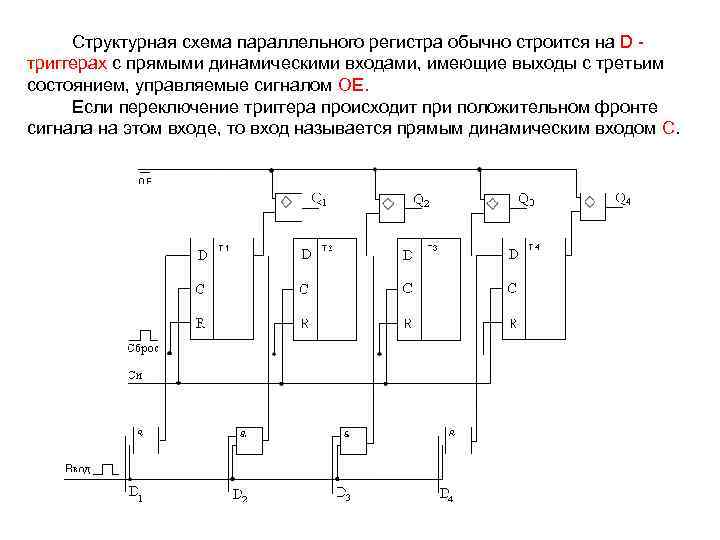Структурная схема параллельного регистра обычно строится на D триггерах с прямыми динамическими входами, имеющие выходы с третьим состоянием, управляемые сигналом ОЕ. Если переключение триггера происходит при положительном фронте сигнала на этом входе, то вход называется прямым динамическим входом С.

Перед записью двоичного числа все триггеры устанавливаются в состояние 0 подачей импульса по входу “Сброс”. Для записи в регистр входной информации подают импульс записи, открывающий входные элементы И. Код входного числа записывается в регистр. По окончании сигнала записи информация, записанная в регистр, сохраняется, несмотря на то, что входная информация может изменяться. Для вывода информации подают импульс по входу “Вывод” (ОЕ). На выходные шины регистра передается код числа, записанный в регистр. При этом число записанное в регистр сохраняется. Для получения новой информации описанные сигналы повторяются.

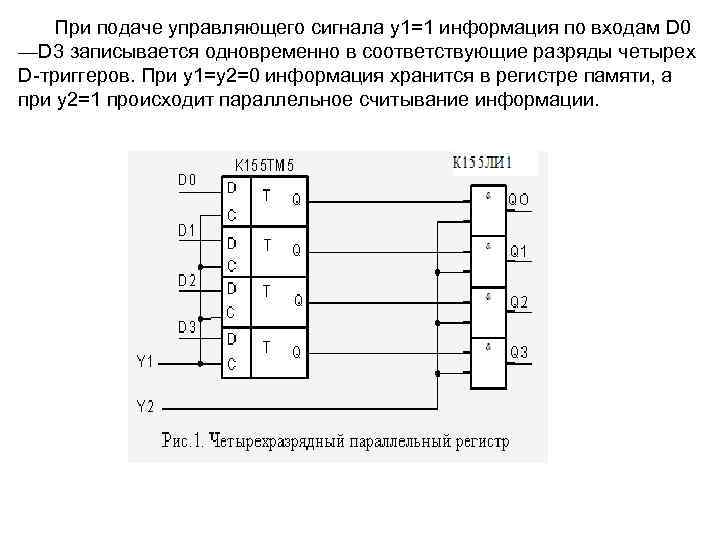При подаче управляющего сигнала у1=1 информация по входам D 0 —D 3 записывается одновременно в соответствующие разряды четырех D триггеров. При y 1=y 2=0 информация хранится в регистре памяти, а при y 2=1 происходит параллельное считывание информации.

Последовательные регистры (регистры сдвига) характеризуются записью числа последовательным вводом. Регистр состоит из последовательно соединенных двоичных ячеек памяти, состояния которых передаются (сдвигаются) на последующие ячейки под действием тактовых импульсов. Тактовые импульсы управляют работой регистра. Регистры сдвига могут управляться одной последовательностью тактовых импульсов. В этом случае регистры называют однотактными. При управлении двумя, тремя, четырьмя и т. д. последовательностями тактовых импульсов регистры соответственно относят к двух , трех , и четырехтактным, а в общем случае к многотактным.

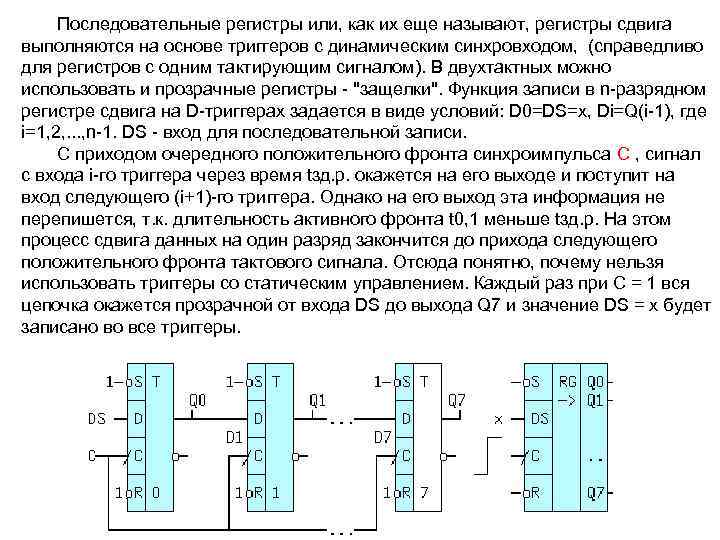Последовательные регистры или, как их еще называют, регистры сдвига выполняются на основе триггеров с динамическим синхровходом, (справедливо для регистров с одним тактирующим сигналом). В двухтактных можно использовать и прозрачные регистры "защелки". Функция записи в n разрядном регистре сдвига на D триггерах задается в виде условий: D 0=DS=x, Di=Q(i 1), где i=1, 2, . . . , n 1. DS вход для последовательной записи. С приходом очередного положительного фронта синхроимпульса C , сигнал с входа i го триггера через время tзд. р. окажется на его выходе и поступит на вход следующего (i+1) го триггера. Однако на его выход эта информация не перепишется, т. к. длительность активного фронта t 0, 1 меньше tзд. р. На этом процесс сдвига данных на один разряд закончится до прихода следующего положительного фронта тактового сигнала. Отсюда понятно, почему нельзя использовать триггеры со статическим управлением. Каждый раз при C = 1 вся цепочка окажется прозрачной от входа DS до выхода Q 7 и значение DS = x будет записано во все триггеры.

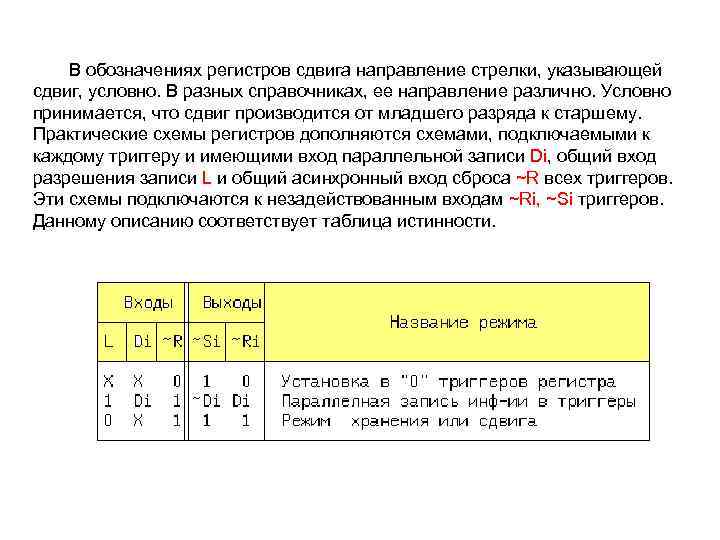В обозначениях регистров сдвига направление стрелки, указывающей сдвиг, условно. В разных справочниках, ее направление различно. Условно принимается, что сдвиг производится от младшего разряда к старшему. Практические схемы регистров дополняются схемами, подключаемыми к каждому триггеру и имеющими вход параллельной записи Di, общий вход разрешения записи L и общий асинхронный вход сброса ~R всех триггеров. Эти схемы подключаются к незадействованным входам ~Ri, ~Si триггеров. Данному описанию соответствует таблица истинности.

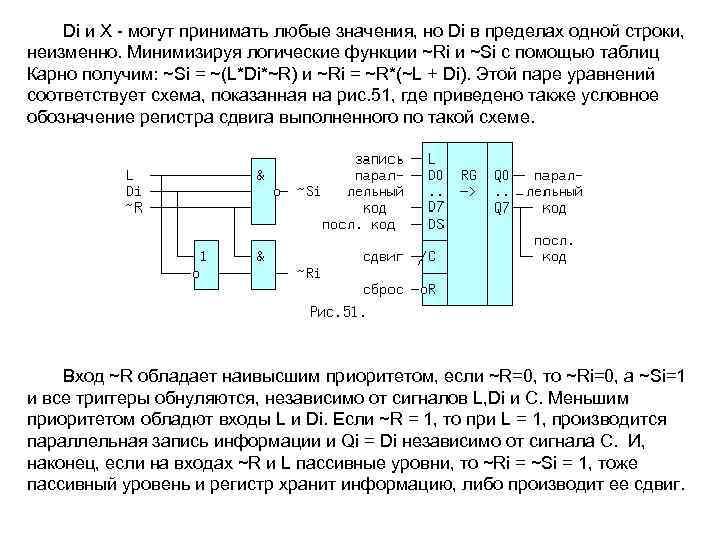Di и X могут принимать любые значения, но Di в пределах одной строки, неизменно. Минимизируя логические функции ~Ri и ~Si с помощью таблиц Карно получим: ~Si = ~(L*Di*~R) и ~Ri = ~R*(~L + Di). Этой паре уравнений соответствует схема, показанная на рис. 51, где приведено также условное обозначение регистра сдвига выполненного по такой схеме. Вход ~R обладает наивысшим приоритетом, если ~R=0, то ~Ri=0, а ~Si=1 и все триггеры обнуляются, независимо от сигналов L, Di и C. Меньшим приоритетом обладют входы L и Di. Если ~R = 1, то при L = 1, производится параллельная запись информации и Qi = Di независимо от сигнала C. И, наконец, если на входах ~R и L пассивные уровни, то ~Ri = ~Si = 1, тоже пассивный уровень и регистр хранит информацию, либо производит ее сдвиг.

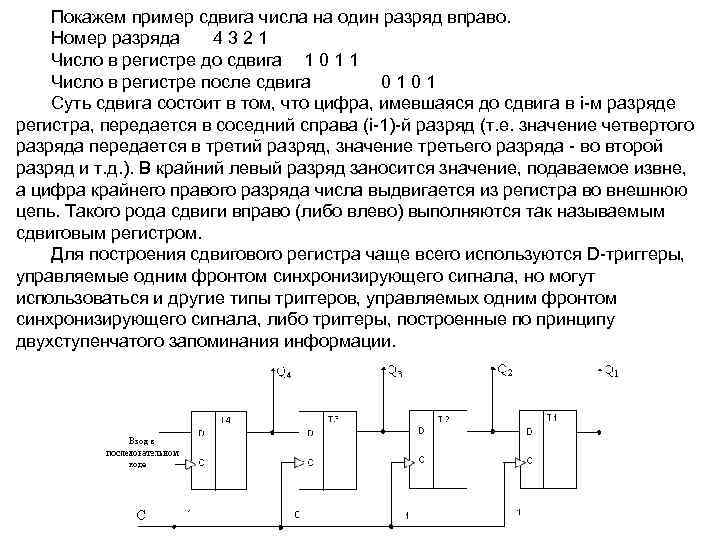Покажем пример сдвига числа на один разряд вправо. Номер разряда 4 3 2 1 Число в регистре до сдвига 1 0 1 1 Число в регистре после сдвига 0 1 Суть сдвига состоит в том, что цифра, имевшаяся до сдвига в i м разряде регистра, передается в соседний справа (i 1) й разряд (т. е. значение четвертого разряда передается в третий разряд, значение третьего разряда во второй разряд и т. д. ). В крайний левый разряд заносится значение, подаваемое извне, а цифра крайнего правого разряда числа выдвигается из регистра во внешнюю цепь. Такого рода сдвиги вправо (либо влево) выполняются так называемым сдвиговым регистром. Для построения сдвигового регистра чаще всего используются D триггеры, управляемые одним фронтом синхронизирующего сигнала, но могут использоваться и другие типы триггеров, управляемых одним фронтом синхронизирующего сигнала, либо триггеры, построенные по принципу двухступенчатого запоминания информации.

Рассмотрим работу показанного сдвигового регистра, построенного на D триггерах. Выход Q триггера каждого разряда подключен к входу D триггера соседнего более младшего разряда. Таким образом, при низком уровне синхронизирующего сигнала хранящееся в триггере значение разряда числа передается на вход триггера соседнего справа разряда и производит в нем подготовку управляющих цепей, В момент положительного фронта синхрони зирующего сигнала каждый из триггеров устанавливается в состояние, соответствующее действовавшему на входе D сигналу, и число в регистре оказывается сдвинутым вправо на один разряд; в старший разряд заносится значение, подаваемое извне на вход D триггера этого разряда. Для осуществления сдвига влево необходимо в сдвиговом регистре изменить связи между триггерами, подключая выход триггера ко входу D триггера соседнего слева (более старшего) разряда. Рассмотрим временную диаграмму, иллюстрирующую процесс записи информации в регистр при вводе числа 1011 последовательно разряд за разрядом, начиная с младшего разряда.

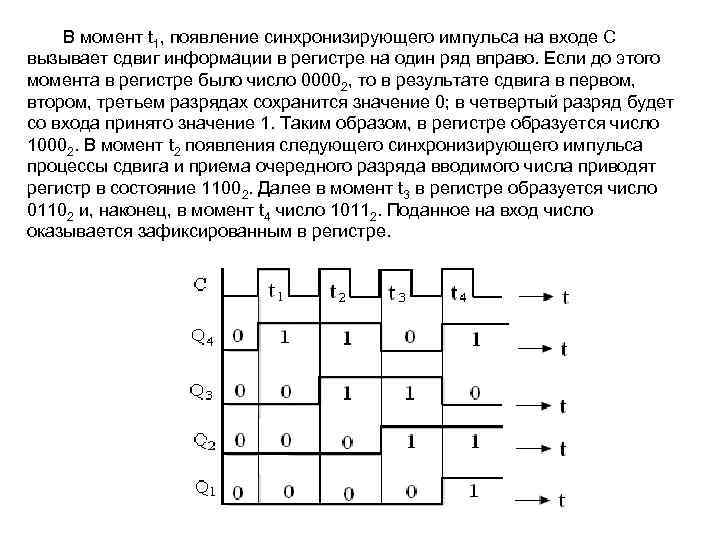В момент t 1, появление синхронизирующего импульса на входе С вызывает сдвиг информации в регистре на один ряд вправо. Если до этого момента в регистре было число 00002, то в результате сдвига в первом, втором, третьем разрядах сохранится значение 0; в четвертый разряд будет со входа принято значение 1. Таким образом, в регистре образуется число 10002. В момент t 2 появления следующего синхронизирующего импульса процессы сдвига и приема очередного разряда вводимого числа приводят регистр в состояние 11002. Далее в момент t 3 в регистре образуется число 01102 и, наконец, в момент t 4 число 10112. Поданное на вход число оказывается зафиксированным в регистре.

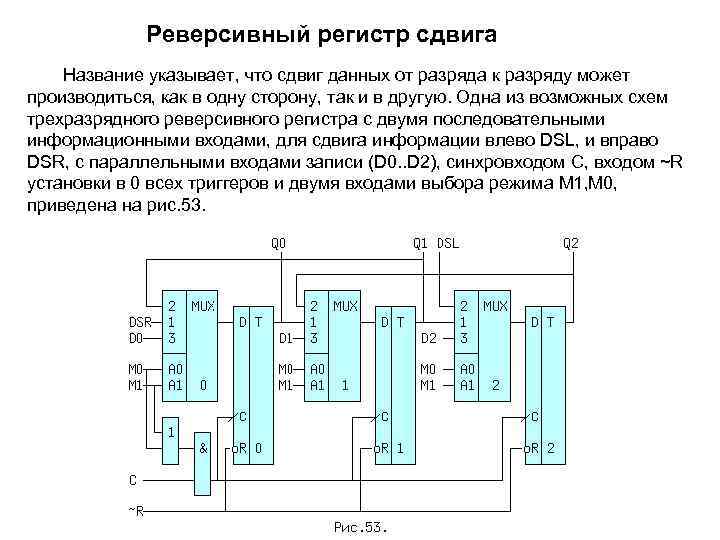Реверсивный регистр сдвига Название указывает, что сдвиг данных от разряда к разряду может производиться, как в одну сторону, так и в другую. Одна из возможных схем трехразрядного реверсивного регистра с двумя последовательными информационными входами, для сдвига информации влево DSL, и вправо DSR, с параллельными входами записи (D 0. . D 2), синхровходом C, входом ~R установки в 0 всех триггеров и двумя входами выбора режима M 1, M 0, приведена на рис. 53.

К D входу любого разряда, за исключением крайних, подключены, через входы 1 и 2 мультиплексора, выходы и левого и правого соседних триггеров. Если M 1=0, а M 0=1, то к входам D подключены первые входы мультиплексоров и информация в каждый триггер, кроме нулевого записывается от левого соседа (происходит сдвиг вправо). Вход DSR служит в этом режиме для последовательного ввода информации. Если M 1=1, M 0=0, то к входам D подключены вторые входы мультиплексоров и информация в каждый триггер, кроме последнего записывается от правого соседа (происходит сдвиг влево). Для последовательного ввода данных в этом режиме используется вход DSL. При M 1=M 0=1 происходит параллельная запись Qi=Di положительным фронтом тактового сигнала. Для хранения информации необходимо подать комбинацию M 1=M 0=0. В этом случае к D входам триггеров подключатся нулевые входы мультиплексоров (на схеме не показаны). Чтобы не произошло несанкционированной записи схема ИЛИ И запрещает в этом режиме прохождение синхроимпульсов. По такой схеме выполнен 8 разрядный регистр 1533 ИР 13. Реверсивный регистр может использоваться для быстрого (всего за n тактов) деления и умножения двоичных чисел на 2^n, где n число сдвигов. Например вместо числа 5, после сдвига влево на 2 разряда, стало число 20.

Синхронный и асинхронный способы загрузки параллельного кода Устройства (в том числе регистры), в которых для записи входного параллельного кода Di используется сигнал разрешения записи L, а тактовый сигнал C не используется, называются устройствами с асинхронной параллельной записью кода. Устройства (в том числе регистры), в которых для записи входного параллельного кода Di необходим, во первых, сигнал разрешения записи L и, во вторых, перепад синхросигнала на тактовом входе C называются устройствами с синхронной параллельной записью кода.

Реализация регистров на интегральных микросхемах К 155 ИР 1 Четырёхразрядный сдвиговый регистр. S 1 – вход для последовательного ввода D 0 – D 3 – входы для параллельных данных С 1, С 2 – тактовые входы. С 1↓ режим сдвига, С 2↓ режим параллельной загрузки. (↓ по отрицательному пепепаду). От любого из 5 входа данных код числа поступит на выходы синхронно с отрицательным кодом. РЕ – разрешение параллельной загрузки, выбор режима работы 1 – разрешается работа регистра по тактовому входу С 2, и в момент отрицательного перепада в регистр загружаются данные (D 0 – D 3) 0 – разрешается работа регистра по тактовому входу С 1, и в момент отрицательного перепада в регистр загружаются данные (D 0 – D 3) Отрицательные фронты последовательностей тактовых импульсов поступающих на С 1 сдвигают данные послед. входа S 1 влево от младшего к старшему) Сдвиг данных по регистру вправо можно получить, если соединить Q 3 и D 2, Q 2 и D 1 , Q 1 и D 0, т. е. старшие с младшими. . Затем перевести в параллельный режим, подав на РЕ = 1. причем, РЕ можно менять когда на С 1 и С 2 низкий уровень.

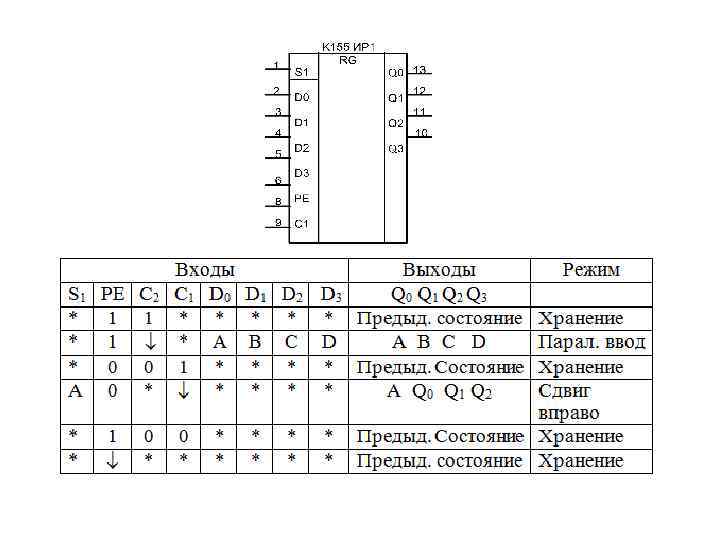
Счетчики Счетчиком называется последовательностное устройство, предназначенное для счета входных импульсов и фиксации их числа. Основное функциональное назначение счетчиков: • • счет импульсов, поступивших на вход; деление частоты. В счетчиках выполняются следующие операции: • установка в нулевое состояние (сброс); • запись входной информации в параллельной форме – начального кода, с которого начинается счет; • хранение записанной информации; • выдача хранимой информации в параллельной форме; • инкремент – увеличение хранящегося числа на единицу; • декремент – уменьшение хранящегося числа на единицу.

По значению модуля счета различают: двоичные счетчики, модуль счета равен целой степени числа два М=2 n , где n – число используемых триггеров; двоично кодированные, модуль счета любое число; По направлению счета счетчики бывают: суммирующие (прямого счета); вычитающие (обратного счета); реверсивные, в которых по управляющему сигналу происходит изменение направление счета. По способу кодирования различают: счетчики Джонсона, счетчики с кодом « 1 из N» , счетчики в коде Грея и т. д. Наиболее распространены двоичные счетчики, все другие могут быть получены из них путем установления дополнительных связей между разрядами. По способу переключения триггеров во время счета счетчики делятся: асинхронные ; синхронные.

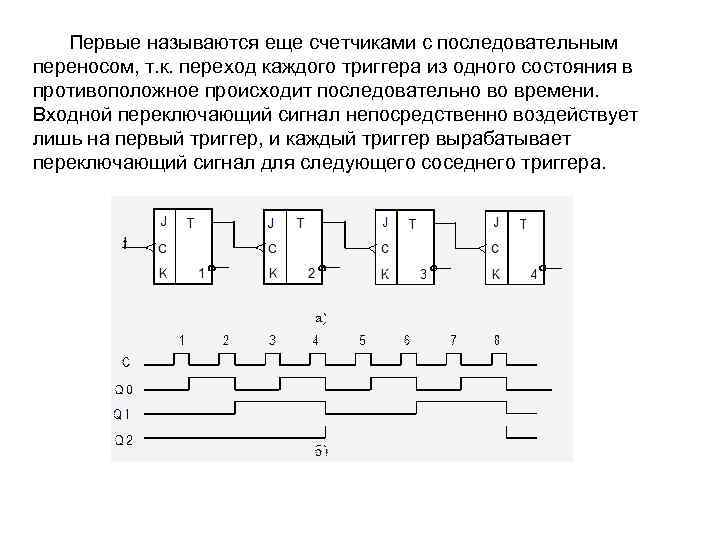Первые называются еще счетчиками с последовательным переносом, т. к. переход каждого триггера из одного состояния в противоположное происходит последовательно во времени. Входной переключающий сигнал непосредственно воздействует лишь на первый триггер, и каждый триггер вырабатывает переключающий сигнал для следующего соседнего триггера.

Лабораторная № 1. Синтез комбинационных схем с одним выходом. Минимизация переключательных функций Лабораторная № 2. Логические функции из Панфилова на Electronics Workbench Лабораторная № 3. Реализация логических функций на мультиплексорах (Proteus). Лабораторная № 4. Построение преобразователя кода на дешифраторах (Proteus). Лабораторная № 5. Микроконтроллер 80 С 51. Подключение светодиодов и кнопки. (Proteus). Задачи А и Б. Лабораторная № 6. Микроконтроллер 80 С 51. Освоение работы с таблицами. (Proteus). Задачи А и Б.