Связь Функциональная Статистическая

Связь Функциональная Статистическая Корреляционная Сопряженность

Определить наличие и силу связи какого-либо признака, с одним или несколькими другими признаками; Определить наличие и силу связи какой-либо величины, характеризующей результативный признак, с одним или несколькими факторных признаков; Определить наличие и силу зависимости какого- либо признака, от одного или нескольких других признаков; Определить наличие и силу зависимости какой- либо величины, характеризующей результативный признак, от одного или нескольких факторных признаков.

Ключевые принципы оценки статистической связи Принцип ковариации. - Описывает параллельное изменение двух или нескольких рядов количественных признаков. В математическом отношении задача сводится к определению мер взаимных численных изменений взаимосвязанных признаков – коэффициентов корреляции. Принцип взаимной сопряженности - Описывает связь между двумя событиями, когда с появлением одного события происходит другое событие. Свидетельством присутствия сопряженности является статистическая значимость, отличия от нулевой гипотезы, отрицающей такую взаимосвязь событий. Эта значимость устанавливается с помощью коэффициентов сопряженности

Задачи, решаемые в ходе анализа статистической связи Ø Установление направления (прямая или обратная) и формы (линейная или нелинейная) связи; Ø Оценка тесноты (силы, плотности) связи; Ø Оценка репрезентативности статистических оценок взаимосвязей, полученных по выборочным данным (величина ошибки, доверительный интервал, уровень значимости). Ø Вычисление величины детерминации (доли взаимовлияния) коррелируемых факторов.

Численные критерии статистической связи Корреляционная связь Сопряженность 1. Для оценки взаимосвязи парных 1. Для оценки взаимосвязи количественных признаков: качественных признаков можно применять u коэффициенты линейной (нелиней- рассчитываемые на основе ной) регрессии таблиц сопряженности u коэффициенты линейной (нелиней- ной) корреляции. u коэффициент ассоциации Юла (Q) 2. Для оценки взаимосвязи нескольких количественных признаков: u коэффициент контингенции (Ф ) u коэффициенты множественной регрессии u коэффициенты множественной или сопряженности (С) частной, парциальной корреляции. u Коэффициент Чупрова (К) и 3. Для признаков сформированных в др. порядковой (ранговой, балльной) шкале: u ранговые коэффициенты линейной корреляции Пирсона или Кендэла.

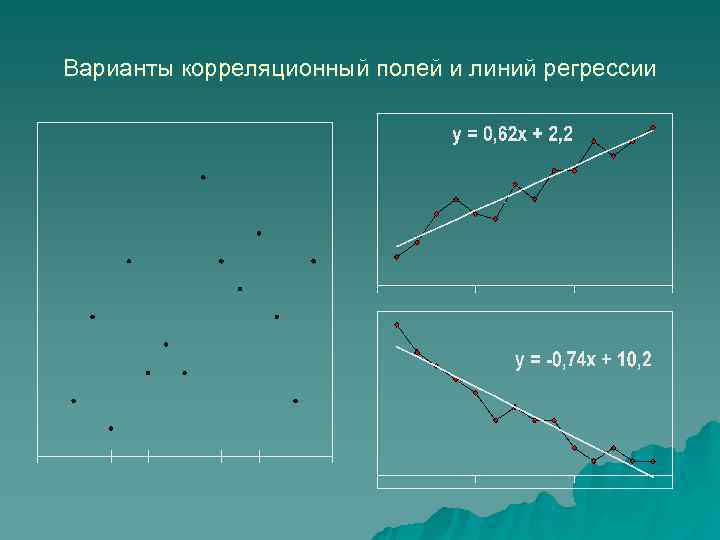
Варианты корреляционный полей и линий регрессии

Индекс Брока u. Y – нормальный вес (кг) u Х – рост (см) u b – поправочный коэффициент для возрастных групп u a – коэффициент 100

Длина шага u. Y – длина шага человека (см) u Х – рост (см) u a – поправочный коэффициент 37

Пример вычисления выборочного уравнения регрессии по пяти наблюдениям i xi yi xi 2 xiyi 1 2. 0 2. 6 4. 0 5. 2. 2 4. 0 1. 8 16. 0 7. 2 3 7. 0 1. 3 49. 0 9. 1 4 5. 0 1. 1 25. 0 5. 5 3. 0 2. 4 9. 0 7. 2 Σ 21. 0 9. 2 103. 0 34. 2 Ø Параметры

Пример вычисления выборочного уравнения регрессии по пяти наблюдениям Полная ошибка результатов наблюдений для уравнения .

Вычисление должной величины показателей жизненной емкости легких (ЖЕЛ) для мужчин в возрасте 18 -25 лет (по Р. Ф. Клемент и соавт. ) Ø Уравнение регрессии Ø Где y - ЖЕЛ Ø β 0 - константа -6, 908 Ø β 1 - коэффициент по росту 5, 8 Ø β 2 - коэффициент по возрасту 0, 085 Ø X 1 - рост Ø X 2 - возраст Ø Для мужчины в возрасте 19 лет, имеющему рост 1, 8 м , Ø ЖЕЛ=-6, 908+5, 8 1, 8+0, 085 19=5, 2 л.

Ковариационное соотношение

Распределение значений коэффициента корреляции Пирсона Направление связи Сила связи Обратная Прямая Связи нет 0 Слабая От 0 до - 0, 3 От 0 до + 0, 3 Средняя От -0, 3 до -0, 7 От +0, 3 до +0, 7 Сильная От -0, 7 до -1, 0 От + 0, 7 до +1, 0 Полная -1, 0 +1, 0 (функциональная)

Коэффициент линейной корреляции (Пирсона) x y x 2 y 2 xy 6 1 36 1 6 8 1 64 1 8 7 2 49 4 28 6 3 36 6 18 5 4 25 4 20 8 5 64 25 40 6 5 36 25 35 9 6 81 36 54 Σx=70 Σy=36 Σx 2=508 Σy 2=162 Σxy=262 r 2=0, 41. = 0, 17

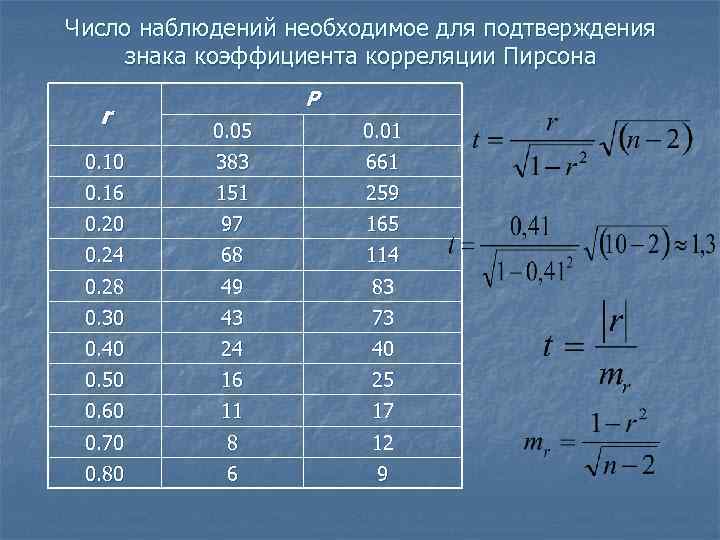
Число наблюдений необходимое для подтверждения знака коэффициента корреляции Пирсона P r 0. 05 0. 01 0. 10 383 661 0. 16 151 259 0. 20 97 165 0. 24 68 114 0. 28 49 83 0. 30 43 73 0. 40 24 40 0. 50 16 25 0. 60 11 17 0. 70 8 12 0. 80 6 9

Соотношение коэффициентов корреляции и регрессии

Корреляционное отношение ( ) . Криволинейная кореляция

Частная, парциальая корреляция Время Число Работ Ошибок страниц ы текста 1 2 3 4 5 4 1 6 6 3 6 2 3 6 6 5 6 4 r 12 2 7 3 0. 4 r 12. 3 0. 2 1 8 1 r 13 -0. 7 R 13. 2 -0. 1 5 8 3 r 23 6 9 1 -0. 4 R 23. 1 -0. 7 6 9 1

Коэффициент множественной корреляции

Коэффициент ранговой корреляции Спирмена Одно из главных достоинств коэффициента корреляции рангов заключается в простоте вычислений. Его применение рекомендовано в случаях: • когда необходимо быстро, ориентировочно определить связь между какими то признаками; • если необходимо оценить связь между качественными и количественными признаками или только между качественными признаками; • когда распределение значений учетных признаков (в том числе и количественных) не соответствует нормальному распределению или распределение неизвестно.

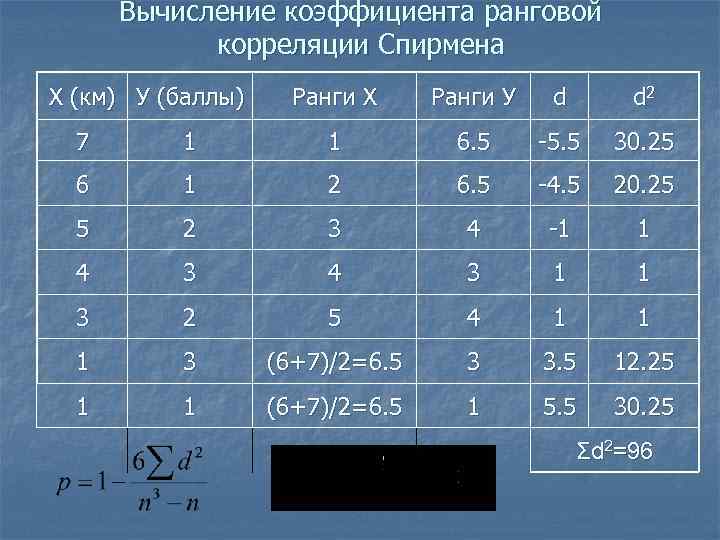
Вычисление коэффициента ранговой корреляции Спирмена Х (км) У (баллы) Ранги Х Ранги У d d 2 7 1 1 6. 5 -5. 5 30. 25 6 1 2 6. 5 -4. 5 20. 25 5 2 3 4 -1 1 4 3 1 1 3 2 5 4 1 1 1 3 (6+7)/2=6. 5 3 3. 5 12. 25 1 1 (6+7)/2=6. 5 1 5. 5 30. 25 Σd 2=96

Вычисление коэффициентов Q и Ф n Распределение рабочих по случаям заболеваний в году Профессии Болели Не болели Итого Станочники 78 83 161 Слесари 30 92 122 Всего 108 175 283

Коэффициенты сопряженности Пирсона (С) и Чупрова (К) Взаимосвязь заболеваемости с ВУТ и профессиональной принадлежности работников предприятия Кратность заболевания в году Профессия Итого Не болели 1 -2 раза 3 и более Станочники 11 12 23 46 Слесари 17 13 24 57 Прочие 72 11 26 109 Всего 100 39 73 212